基于MIC-TCN-Attention的抽水蓄能机组发电电动机定子温度预警方法研究
2021-08-07常玉红吴月超宋旭峰王大强李超顺
常玉红,吴月超,何 铮,宋旭峰,王大强,李超顺
(1.国网新源控股有限公司,北京100000;2.中国电建集团华东勘测设计研究院有限公司,杭州311122;3.浙江仙居抽水蓄能有限公司,浙江仙居317300;4.华东琅琊山抽水蓄能有限责任公司,安徽滁州239000;5.华中科技大学土木与水利工程学院,武汉430073;6.浙江大学电气工程学院,杭州310027)
0 引 言
定子作为抽蓄机组发电电动机重要部件之一,其受损直接影响电站的发电量、发电效率,以及电站的运行故障并造成停机。定子温度作为可观测变量,发展趋势与机组个部件受损情况密切相关,其原理为机组做能量转换时,出现的各种损耗如机械损耗、电损耗、铁损耗等产生热量,损耗较大时,温升会出现异常状态,以监测温度判断设备受损情况也是被证实过的可行方案。例如:负荷升高会引起电机温度升高;励磁电流增大导致转子发热,绝缘受损造成片间短路而引起铁芯发热严重[1-3]。而传统设备温度监测通常利用内部置入传感器测量并以运行人员经验去判断温度趋势,此方案可靠性差,对人员要求高,易出现较多的误报警。而常见的温度故障检测系统通常有模型分析、数据驱动等方式,其中数据驱动对于复杂系统的检测、诊断、预测有明显的优势[4,5]。随着深度学习(Deep learning,DL)的发展,考虑多源变量的数据分析监测模型受到了广泛的关注。文献[6]利用循环神经网络(Recurrent neural network RNN)实现了风电机组主轴承温度预警。针对时序预警序列,文献[7,8],运用长短期记忆网络(Long short terms memory,LSTM)建立监测系统,并得到了较好的效果。然而,现有的模型和方法在抽蓄机组发电电动机温度预测方面存在不足。但对实时预警系统而言,大规模监测需考虑成百上千的通道,模型的运行效率显得尤为重要。RNN 网络对序列信号需要依次处理,耗时较长。抽蓄机组设备发热散热过程复杂,RNN 预测效果对邻近输入依赖性较高,当序列数据存在急剧变化的现象时,其预测效果会出现较大误差[9]。而近来较为流行、具有较强非线性处理能力的卷积神经网络(Convolution neural network,CNN)对时序信号挖掘能力较弱,预测精度相对较差。
时间卷积网络(Temporal Convolutional Network,TCN)是一种新的时序模型,利用了CNN 优势,扩展卷积并增加时序视野区间,实现输入输出并发,减少大量训练时间,同时拥有较好时序信息挖掘能力,在多个时序预测领域已得到验证[10]。因此,本文以定子线圈温度为预测变量,考虑多个环境变量,建立以TCN-Attention 架构为基础的深度实时预测模型,并与其他预测模型进行比较,结果表明所提方法具有较高预测精度和稳定性。
其次,实时预警方面,传统预警策略仅考虑预测值与历史值之间的差异,当温度达到某一规定的阈值或发生显著变化时进行报警。此方案存在两个问题,一是早期故障征兆数据获取受环境影响,偶发的异常数据将导致系统误报,给设备维护人员造成“报警疲劳”;二是预警稳定性较差,无法精确找到设备异常状态,换句话说,对设备细微故障差异性不能及时发现以至于晚报频繁[11,12]。因此,本文提出一种基于统计学理论的预警策略,利用随时间变化的时序残差集,以动态划分实时残差序列统计指标峰度、偏度判断设备运行情况,以到达实时预警准确性的目的,并设计相关实验验证了所提方案的有效性,对机组状态趋势预判和运维策略提供更可靠的指导意义。
1 研究方法
1.1 方法框架
为设计出一套能适应抽蓄机组发电电动机的定子温度预警系统,本文提出了一种基于最大相关系数与时间卷积网络的预警模型,具体方案设计如图1 所示:总体分为两个阶段,离线阶段和在线阶段。
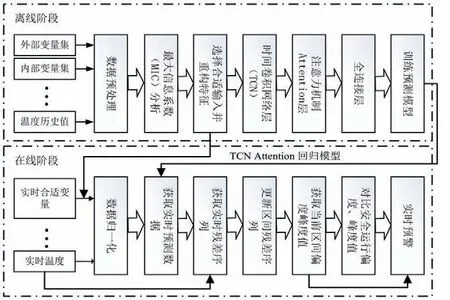
图1 总体方案Fig.1 Model framework
离线阶段具体步骤为:步骤1:获取历史变量集,温度集;步骤2:为了选择合适的数据结构,利用MIC 分析了相关变量集;步骤3:进行多次实验并选择合适输入变量结构;步骤4:训练TCN-Attention实时预测模型并测试其效果。
在线阶段步骤为:步骤1:获取实时变量、温度集;步骤2:利用训练好的TCN-Attention 模型获取实时预测值;步骤3:为更好分析系统运行情况,以残差序列为基础,滚动划分序列区间;步骤4:建立区域性统计模型,设置经验阈值,并实现系统的实时预警。
1.2 建立离线分析模型
1.2.1 构建多源信息输入
发电电动机定子线圈发热和散热过程较为复杂,选择合适的输入能较好地拟合温度趋势并减少模型复杂度。因此,本文首先考虑可能影响电动机定子线圈温度主要因素,内部因素包括定子线圈温度、铁芯温度、上下齿压板温度等;外部包括机端有功功率、无功功率、水头、轴承x、y方向摆度、轴向位移、转速等;然后分析定子线圈温度Fstator与其他变量集F=的关联程度。最大信息系数(MIC)基于信息论互信息理论,相比其他相关性分析方法例如Pearson、Spearman,MIC 能更好地捕捉变量间的非线性关系,且计算复杂度低,鲁棒性高[13,14]。因此本文利用MIC 作为变量分析,以本文为例能够被定义为:


1.2.2 建立TCN-Attention预测模型
网络模型分3 个模块,时间卷积网络层、注意力机制层,全连接层。模型结构见图2 所示:其中TCN 是由堆叠扩张卷积和因果卷积层,同时结合残差而成的新网络结构,这个结构能够继承CNN 全面提取优点,又能够通过控制其卷积核大小,扩张系数等参数适应各种时序任务。 在本文当中,{(x1,x2,…,xn)1,(x1,x2,…,xn)2,…,(x1,x2,…,xn)t}为输入,其中(x1,x2,…,xn)表示输入向量,n表示特征数,t表示滑动步数;首先通过因果卷积层(Causal Convolutions),此层为严格的单向结构,对于上一层T时刻的值,只依赖于下一层T时刻及其之前的值;其次,利用一维全卷积层来保留整个输入序列并构建长期记忆;最后在膨胀卷积层(Dilated Convolutions)设置扩张系数d并进行间隔采样。序列向量(x1,x2,…,xn)s上扩张卷积运算F可定义为:
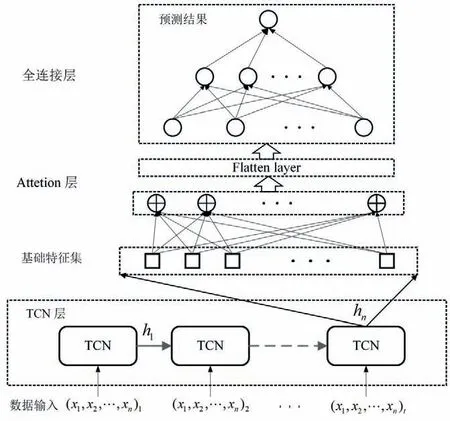
图2 TCN-Attention网络结构Fig.2 Network structure of TCN-Attention

式中:k为卷积核大小;(s-d·i)表示采用上层的第(s-d·i)元素。为了进一步对TCN 输出特征集进行优化,在网络模型的第二部分,采用了Attention 层进行权值筛选,具体步骤为,首先对基础特征集(h1,h2,…,hT)进行相似性得分,得分系数向量集为{(s1,s2,…,sN)1,(s1,s2,…,sN)2,…(s1,s2,…,sN)T};其次利用一个Softmax层进行归一化得到概率系数向量集{(∂1,∂2,…,∂N)1,(∂1,∂2,…,∂N)2,…,(∂1,∂2,…,∂N)T};最后对基础特征向量进行加权求和,结果表示为(c1,c2,…,cT),其中ck能够被描述为:

式中:xi表示上一层的隐藏单元。
网络模型的第三部分,通过Flatten 层连接一个3 层全连接网络建立的回归预测模型并通过前向传递和误差反向传播更新网络权值。
1.3 在线实时预警策略
基于上述离线阶段研究,高精度的定子线圈温度实时预测已经能够实现,但对抽蓄机组设备实时预警系统来说,除了实时预测的高精确度外,高效而准确地提供在线预警是保证机组维护成功与否最重要的一环。感器故障或极端环境影响使机组设备温度等动态指标频繁出现奇异值,过预测值与实际值差异程度预警,易出现误报、晚报现象,相比精确度,稳定性能够更加显著地反映出设备运行状态,因此,本文从设备动态特性出发,以精确性和稳定性为目的,设计出一套适用于当前电站实时预警策略,其中,因电站温度变化不符合常规数据分布,而残差序列作为预测后另一变量,其分布应符合期望μ= 0,σ较小的高斯分布,其中横坐标为误差;又由于极值、方差易受人为干扰,不能客观的反映实际变化情况。因此,本文考虑正态分布检验指标偏度系数与峰度系数监测温度残差,其中偏度是描述数据分布形态的统计量,反映总体取值分布对称性,偏度绝对值越大,其分布形态偏斜程度越大;峰度则能够描述数据分布尾部长短和峰体飕峭的关系,出现异常值时峰值偏大[15]。具体步骤为:首先发电电动机定子线圈温度通过传感器实时更新,经训练好的TCN-Attention网络模型后,并获得实时预测值,计算时间段内残差序列εerror=(ε1,ε2,…,εk,…,εN),其中残差εk被描述为:εk=vraw-vpre其次随时间动态划分区间残差序列,生成子序列N1,N2,…,Ns。其中Nk表示区间[tk-Tinitial,tk]中所有的误差数据,tk表示当前时刻,Tinitial为采样初始时间,序列长度为Tk,定义为Tk=tk-Tinitial;最后计算出当前区间内各时刻残差序列偏度与峰度值分别被定义为:

式中:ηk,σk分别表示序列Nk的均值、标准差。
其中峰度绝对值越大,其分布形态陡缓程度与正态分布的差异程度越大,可描述设备预测精确性,其中越小精确度则越高;而偏度反映了总体取值分布的对称性,偏度绝对值越大,其分布形态偏斜程度越大,即接近0 时,则表示设备运行较为稳定[8]。设置偏度、峰度经验阈值为K、S:其中K、S被定义为:
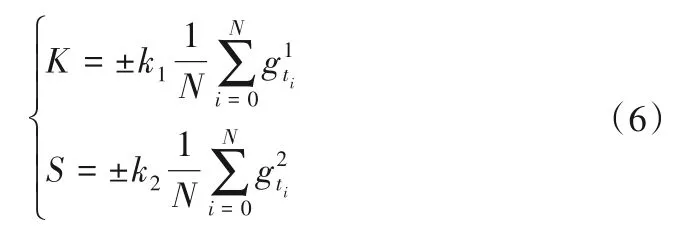
式中:N为当前时刻前区间数;k1和k2可由现场人员根据经验在前端页面确定。
以K、S为基准,由后台在线判断区间内的均值变化,并判断其是否报警。
2 实验验证
2.1 数据描述
实验数据来自于浙江仙居电站机组发电电动机,其由东方电气集团东方电机有限公司制造,为立轴、半伞式、三相、50 Hz、空冷可逆式同步发电电动机。主要由定子、转子、上下导轴承、推力轴承、上下机架、上端轴、主轴和其他发电电动机附件构成。有发电、抽水、发电调相、抽水调相、停机5 种稳定工况,另外还设有黑启动、线路充电(零起升压)等特殊工况。机组发电方向(发电、发电调相、拖动机及线路充电工况)运行时,机组旋转方向俯视为顺时针,机组抽水方向(抽水、抽水调相工况)运行时,旋转方向俯视为逆时针。发电机额定功率375 MW,电动机额定轴输出功率为413 MW,额定电压18 kV,额定电流为13 365/13 751 A,额定励磁电压为456 V,额定励磁电流为1 962 A,额定转速为375 r/min,飞逸转速为555 r/min。
2019年1月4 -5日定子线圈Z1通道超短期温度数据如图3所示。
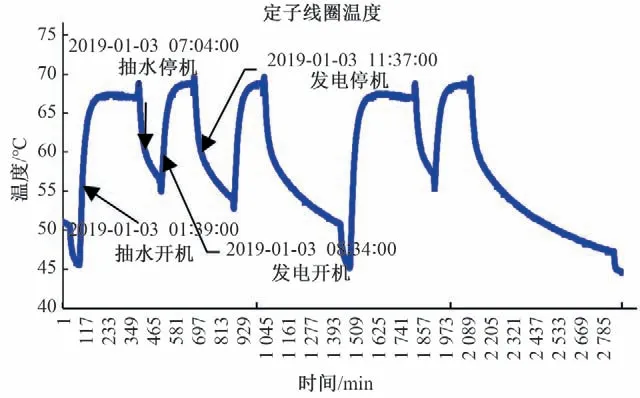
图3 定子线圈Z1温度监测数据Fig.3 Monitoring data of stator coil Z1
如图3 所示,发电电动机开停机频繁,抽水发电交替进行,且每次过程时长不一,时间范围在2~6 h左右,升温降温过程复杂,变化剧烈,温升过程20~35 min,降温过程10~20 min。本次实验以定子线圈温度短期预测为目标,并设计发电、抽水工况开机实时预测预警模型,停机不预测,预测时间为5 min。
2.2 特征分析及重构
本次研究分别分析了发电态、抽水态两种工况的数据,内部变量选择了定子铁芯、定子齿压板、上导轴承、推力轴承、上下机架的时序数据;外部变量选择了水头、有功、无功、冷却水进出口温度、轴向位移,转速。计算上述变量与定子线圈温度的最大相关系数MIC,如图4所示。

图4 其他变量与定子线圈温度MIC分析Fig.4 MIC analysis of other variables and stator coil temperatur
其中,MIC 从大到小排序为有功、无功、励磁电流、电压、水头、冷却水出口温度等。其次,为了确定最优输入维度,本文选择了5 种输入方式作为比较,分别是(定子线圈温度、有功、无功)、(定子线圈温度、有功、无功、励磁电压)、(定子线圈温度、有功、无功、励磁电流、励磁电压)、(定子线圈温度、有功、无功、励磁电流、励磁电压、水头)、(定子线圈温度、有功、无功、励磁电流、励磁电压、水头、冷却水出口温度),结果如图5 所示:图5中输入维度为5 时,其RMSE、MAE、MAPE均为最小,因此本文输入确定为(定子线圈温度、有功、无功、励磁电流、励磁电压)。
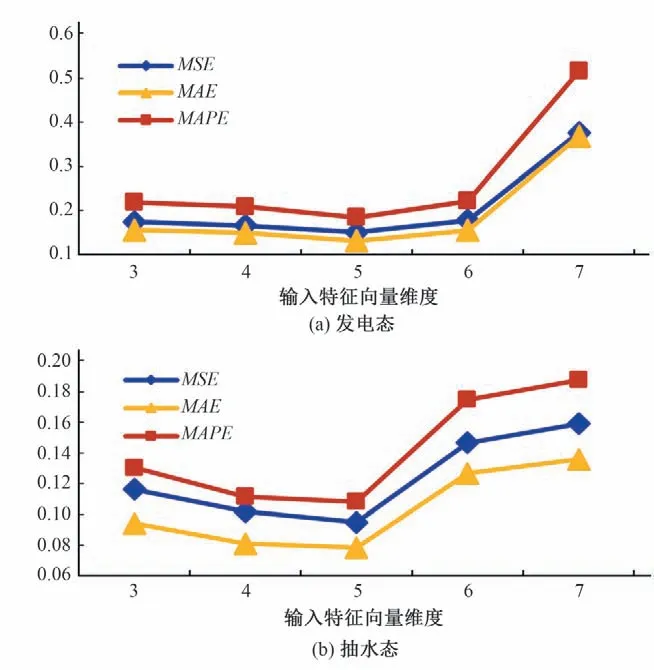
图5 不同输入尺寸的MSE,MAE和MAPE值Fig.5 MSE,MAE and MAPE values for different input dimensions
2.3 预测结果局部比较
为了验证所提模型对复杂升温降温过程的拟合能力,本文又分别比较了升温降温局部预测结果,由于ANN模型整体精确度较低,DGRU-Attention 模型用时较长,均不能较好满足现场需求,因此比较模型选用TCN 和DGRU 模型,其中2020年1月10日抽水态升温降温过程结果如图6 所示,其他测试集局部结果如表3 所示。表中评价指标为16 次抽水17 次发电发热散热RMSE均值:
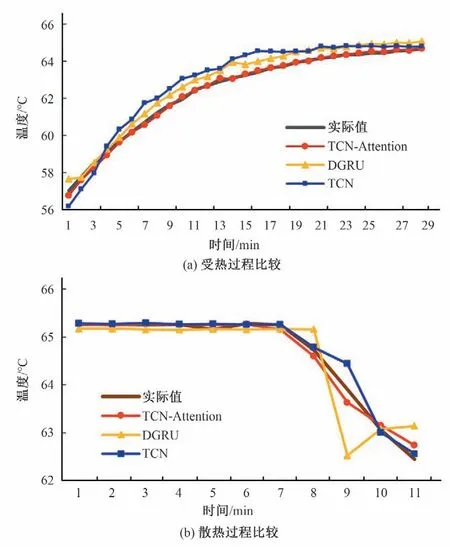
图6 发热散热过程比较Fig.6 Comparison of heating and cooling processes
从图6(a)升温降温过程可以看出,当开机后,各模型拟合效果较好,而10 min 后,温度变化逐渐趋于平缓,此时DGRU 模型出现明显偏高现象;而图6(b)中,DGRU 模型在遇到急剧下降趋势时,拟合效果则出现明显偏低现象,且波动较为剧烈,这是由于GRU网络在学习的过程中,利用历史输入数据进行严格的时序学习,即后一时刻数据只依赖前一时刻输入,因此,前一时刻连续多个输入为上升或下降而下一时刻为平缓期时,GRU网络不可避免会出现偏高偏低现象,而TCN 网络利用卷积对序列数据进行并发学习,拟合曲线会较平滑。但由于卷积的介入,TCN 相比GRU 网络来说,捕捉时序信息能力相对较差,从图6(a)中也明显看出,TCN 网络出现整体偏差较大。而利用Attention 机制,对时序信息权值打分,处理输入信号,能提高整体精确度并改善模型性能。从图6 和表2 中明显看出TCNAttention模型相比DGRU和TCN都有了明显改善。

表2 局部预测性能指标对比Tab.2 Comparison of local prediction performance indicators
2.4 离线阶段模型结果比较
为进一步验证所预测模型优势,与4 个传统深度学习组合模型做了比较,包括TCN 模型、DGRU-Attention 模型、深度ANN模型、DGRU模型,具体的模型参数如表1所示。
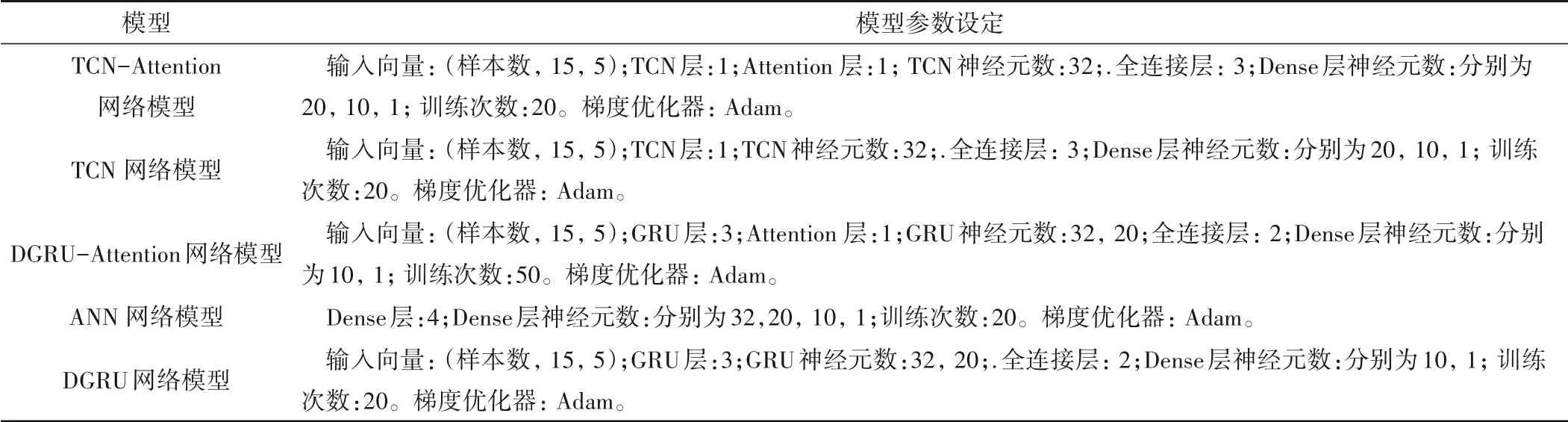
表1 对比模型的参数设置Tab.1 The parameter settings of the comparison models
本文的训练及测试均在在Python 的Pytorch 平台上建立深度神经网络,运行Windows 10 的计算机上采用2.33 GHz Intel Xeon®CPU,RAM 16 GB的微机平台。
基于MIC 系数的分析,模型输入为(定子线圈、有功、无功、励磁电流、励磁电压);并对相关参量进行归一化,由于温度变化受到季节、天气影响较大,因此,此次实验利用设备标幺值统一度量,通过查看设备信息,上述特征标幺值为(115 ℃,393.75 kW,175 kW,1 962 A,465 V);选取2019年1月1日至2019年12月31日运行数据 作 为训练集,2020年1月15 至2020年1月31日运行数据作为测试集,其中测试集中有16 次抽水态、17 次发电态;评价指标为均方差(Root Mean Square Error,RMSE),平均绝对百分比误差(Mean Absolute Percentage Error,MAPE),预测时间Pre Time、训练时间Time。实验结果分别取16 次抽水态、17次发电态的平均误差、时间值,结果如表3所示。

表3 预测性能指标对比Tab.3 Comparison of forecasting performance indexes
模型维护作为智能监测系统不可或缺的部分,模型更新所耗时间被做了比较,表3 中所示:所提模型较GRU-Attention、GRU 减少了74.78,22.19 s,大大减小监测系统运行压力,而相比其他模型的精确度,TCN-Attention 模型优势更加明显,既保证了系统在线监测稳定运行,对于预测精确度又有极大改善。
2.5 在线阶段验证
而对于实时预警系统来说,在线预测时间十分重要,较短的预测训练时间能极大程度改善监测稳定性、精确性,并较少系统运行负荷。从表3中能看出,TCN-Attention 模型较DGRUAttention、DGRU 模型在预测时间上有了明显改善,分别缩短了0.08、0.04 s,这是由于TCN 通过控制卷积核、扩张系数,是的采集视野灵活变动,相比RNN 系列的递归模式,此方式在训练时间上更加有优势;同样的,ANN 模型相比TCN 来说,虽然在预测时间上略有优势,减少了0.03 s,但精确度却远不及GRU、TCN等时序模型,不能满足实际预警需求;最后,比较了TCN-Attention 和TCN,所提出的TCN-Attention 网络结构分别提高了发电态、抽水态精确度约0.07、0.67,预测时间降低了0.01 s,表明Attention机制能够提升精确度,并对模型预测时间影响较小。
针对预警策略的验证,本次在测试集某时刻内分别加入持续性和短期性异常噪声,残差序列如图7 所示。图7 中显示:开机后228 min 加入噪声时,误差出现明显震荡,范围在(-0.15,0.71)之间,228、229 min 出现异常点,而随后15 min 内的预测值又出现在安全运行范围内,如果此时以预测值的奇异序列来判断设备是否故障,连续出现3 个异常点后的系统又趋于长时间稳定,可能造成系统频繁误报、晚报的现象。因此,本文就以此次对象为目标,提出了基于误差滚动序列和统计学理论实时预警策略,首先,对获取的残差序列进行划分,因当前机组设备通常需要20~30 min 稳定,模型预测则需时长为19 min 的历史值,预测时长为5 min,所以设定初始时间Tinitial为开机后29 min,间隔时间T为5 min,生成N1,N2,…,N5454 个残差区间,各区间序列时长分别为10+5*(n-1)分钟;其次滚动实时计算每个划分区间对应偏度峰度,结果如图8 所示。图8 中持续性干扰情况下可明显看到,45 号区间出现较大的偏差,偏度值为2.76,峰度值为14.47,根据经验设定阈值参数N=5,k1=3,k2=3,由式(6)得出设定阈值K=1.83,S=3.39,远小于45 区间的偏度和峰度值,实时预警系统报警,此时运行时刻为(45-1)×5+10=230 min,相比加入噪声的时刻228 min 偏差较小,且满足现场实际需求。其次,在图9 中,短期干扰情况下,45 号区间出现轻微偏差,偏度值为0.61,峰度值为1.07,在设定阈值之内,不报警。可见,当发电电动机出现故障导致其温度异常变化时,本文提出的实时预警策略能及时发现故障并发出报警信息,实现抽蓄机组发电电动机的在线监测。
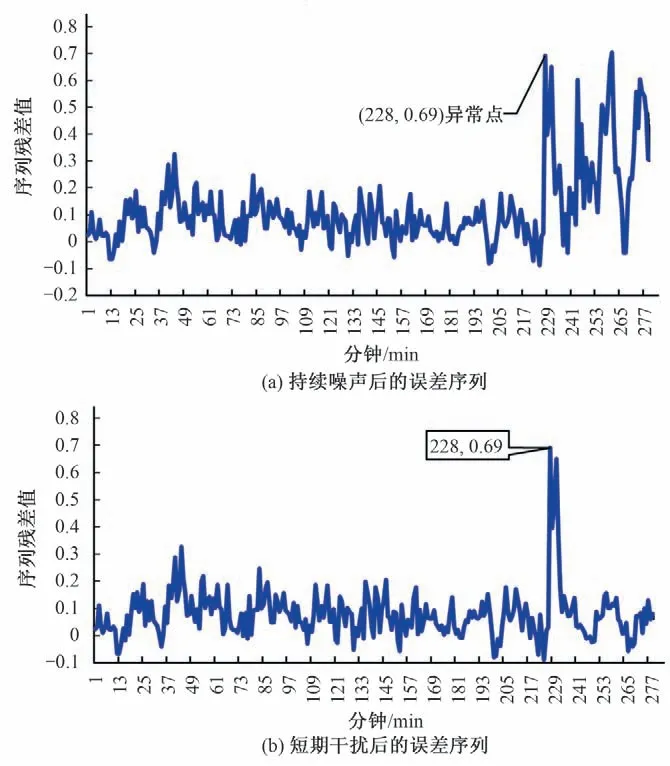
图7 持续噪声后的误差序列与短期干扰后的误差序列Fig.7 Error sequence after continuous noise and Error sequence after short-term interference
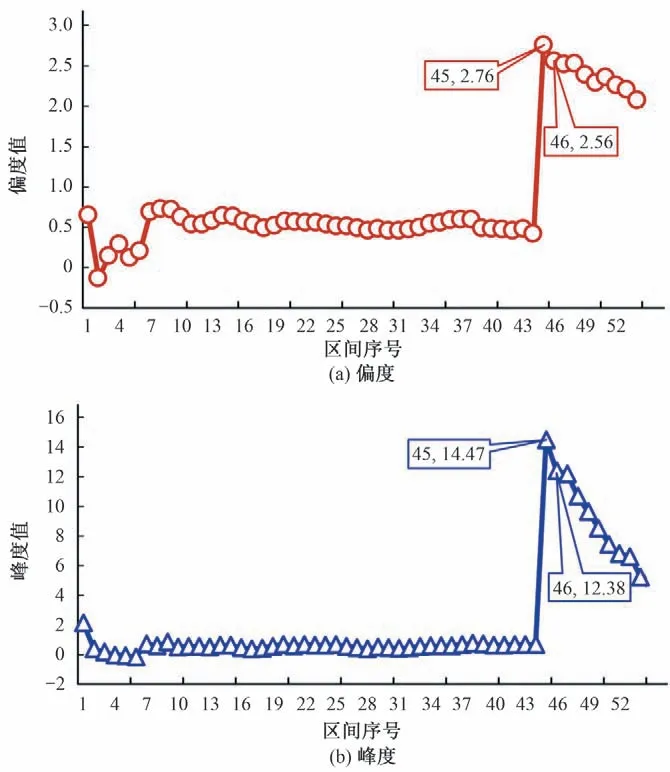
图8 持续干扰下滚动残差区间偏度与峰度值Fig.8 The skewness and kurtosis value of the rolling residual interval after continuous noise

图9 短期干扰下滚动残差区间偏度与峰度值Fig.9 The skewness and kurtosis value of the rolling residual interval after short-term interference
3 结 论
本文以抽蓄机组安全运行为前提,基于大数据分析和深度学习,提出一种TCN-Attention 网络的温度实时预警模型,通过工程实例数据分析验证,得出如下结论。
(1)通过MIC 合理选择与定子线圈温度关联性较强变量;以重构数据为基础,建立定子线圈温度发电态、抽水态短期预测模型,与其他深度组合模型比较,此方案在保证精确度较高的情况下能进一步减小预测和后台训练时间,提高了电站实时监测系统的效率性和准确性。
(2)通过比较各模型定子线圈发热散热过程,验证了TCNAttention 网络模型在保证耗时较小情况下,面对复杂多变的升温降温过程时,较RNN模型有更好的拟合效果。
(3)由于传统的预警策略误报、晚报频繁,考虑残差序列的分布性,结合统计学指标峰度与偏度,设计了一种滚动的实时温度预警策略,并通过设计实验验证了其准时性和准确性。
(4)随着大数据、人工智能的高速发展,短期监测预警系统会应用到各个领域,本文所提出的预警方案可为相关实际应用提供一定参考。
