坡面径流下泥沙起动临界水深研究

何贵平，朱崇林，谢 艳，雷孝章

（1.四川大学水利水电学院，成都610065；2.四川大学水力学与山区河流保护国家重点实验室，成都610065；3.四川省公路规划勘察设计研究院有限公司，成都610041）

0 引 言

泥沙起动问题一直是泥沙运动力学中关注的重点，泥沙起动通常有滚动、滑动、跃移3种模式。在工程应用中，水库排沙、河床演变、航道治理以及桥梁冲刷、水环境保护等方面与泥沙起动均有密切的联系［1］。同时开展泥沙起动研究有助于进一步丰富和发展泥沙运动理论。因此，研究泥沙起动的临界条件对于理论和工程应用方面均有重要的实际意义。

目前，研究泥沙起动的临界条件主要从临界起动切应力、临界起动流速和临界起动功率3 个方面入手。窦国仁［2］将泥沙起动问题总结为3 种状态，将动未动、少量动和普遍动，并根据其发生机率进一步推导出了泥沙起动切应力和起动流速的表达式。何文社等［3］通过考虑相对暴露度、附加质量力等影响因子，采用滚动模式，推得了非均匀沙起动临界无因次切应力公式。刘兴年等［4］分析了粗细化过程中非均匀沙的起动规律，进而导出了非均匀沙分级起动流速的计算公式。张俊宏等［5］对国内外非均匀沙起动研究的成果进行了分析和总结，指出了3 种泥沙起动临界判别条件在各自的应用中存在的问题。程烨等［6］基于颗粒间相对暴露度的分布规律，推导出了3 种泥沙起动模式的起动概率。吴岩等［7］与李林林等［8］分别采用滚动和滑动模型推导出了渗流作用下岸坡泥沙起动流速公式。

综上所述，以往大多数研究都是针对平坡及岸坡上的泥沙起动，对于坡面薄层水流下泥沙起动的研究至今较少。李林林等［9］通过引入附加质量力的办法，采用滑动起动模式，得到了正负坡上泥沙起动概率的计算公式，并进一步推导出了起动标准为中动时的无量纲起动切应力的表达式。朱崇林等［10］通过室内水槽冲刷实验，采用滚动模式并结合斜坡径流-渗流耦合模型推导出了临界水深的理论表达式，但其理论分析中并未考虑到泥沙间相互作用的影响。本文从相对暴露度的角度出发，采用滚动模式建立坡面径流作用下斜坡临界水深的表达式，计算得到的理论值与实测值较为符合，精度较高。

1 理论分析

1.1 暴露度分析

暴露度法是描述非均匀泥沙颗粒之间相互影响的方法之一，均匀沙起动则可以作为非均匀沙起动的一种特殊情况进行处理。另一种方法则通过直接引入附加质量力来表示这种相互影响作用。Paintal［11］在考虑均匀沙在床面上的位置时，提出了涉及相邻上下游颗粒的绝对暴露度的概念。其理论主要是通过平均床面来反映绝对暴露度，并将其作为一个修正项引入作用力表达式。本文采取韩其为等［12］提出的相对暴露度概念，由于泥沙颗粒处于床面的位置随机且作用于颗粒上的水流速度随机，故单颗粒泥沙的起动具有偶然性。为简化这种随机作用，引入了相对暴露度的概念，如图1所示。

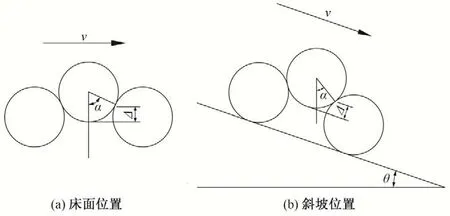
图1 泥沙颗粒暴露度示意图Fig.1 Schematic illustration of exposure of sediment particles to slopes

在床面上，将暴露度Δ定义为所研究颗粒的最低点与下游相邻颗粒接触点的竖向距离，暴露角α则定义为研究颗粒的球心位置同下游相邻颗粒接触点连线与竖直方向的夹角，如图1（a）所示；在斜坡上，本文将暴露度Δ定义为研究颗粒最低点与下游颗粒接触点在垂直斜坡方向上的距离，暴露角α定义不变，如图1（b）所示。其相对值Δ′则统一用暴露度Δ与泥沙颗粒半径R的比值，即Δ/R，来表示。从图中可以看出，当Δ越大时，隐蔽作用越强。

进行均匀沙分析时，Δ′可取为均匀分布，其分布函数为［13］

式中：ξΔ′表示Δ′的随机变量为Δ′的最小值，当泥沙颗粒均匀且紧密排列时，Δ′m=0.134。

由式（1）可求得Δ′的数学期望为［7］：

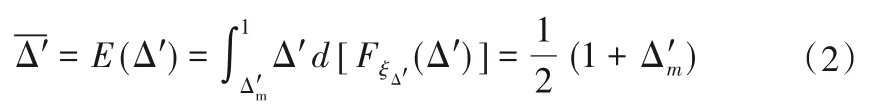
对于非均匀沙，可将泥沙颗粒进一步划分为粗颗粒、中颗粒和细颗粒，并求得各粒组Δ′的数学期望［7，14］。

式（3）～式（5）中：Dl为第l组泥沙粒径为非均匀沙的平均粒径，可用计算；其中，n为分组数，P1，l为床沙组配，即第l粒组泥沙所占质量分数。

1.2 泥沙起动流速公式推导

由图2 可知，在坡度为θ的斜坡上，假设水流方向与斜坡方向平行，且与斜坡水平轴成90°夹角。泥沙在水流作用下所受的力有：水流拖曳力Fd、上举力FL、水下重力W′。由于坡面泥沙起动条件的推导基于的是水流为连续流动的过程，因此忽略垂直渗流的影响。各力分别说明如下：

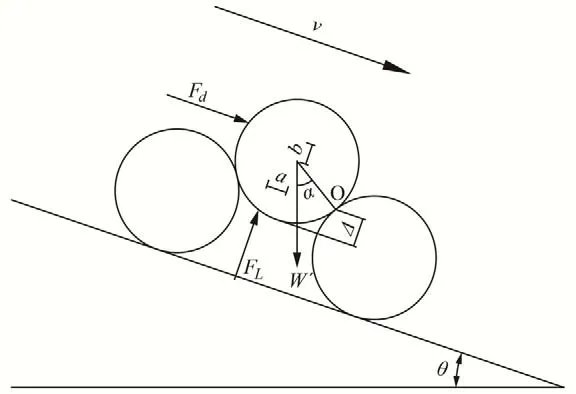
图2 斜坡上泥沙颗粒起动示意图Fig.2 Schematic diagram of sediment particle starting on slope

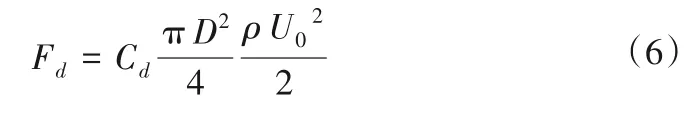
式中：Cd为阻力系数，一般取0.4；CL为上举力系数，一般取0.1；γs、γ分别为泥沙和水的容重；U0为泥沙起动时水流瞬时底速；ρ为水的密度；D为泥沙粒径。

从图2由几何关系还可得：

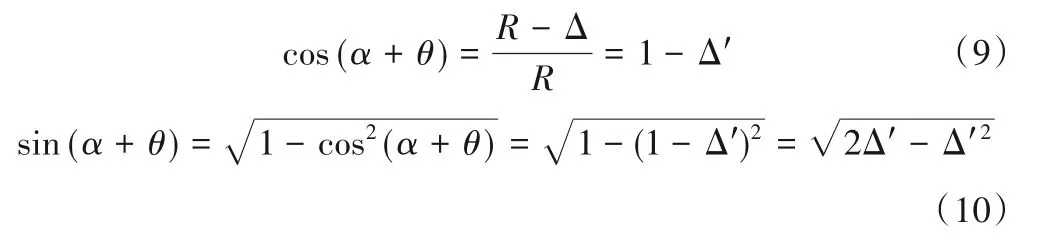
联立式（9）和式（10）可得：

本文采用滚动模式，以所研究泥沙颗粒与下游相邻颗粒相接触点O为起动支点，构建力矩平衡式可得：

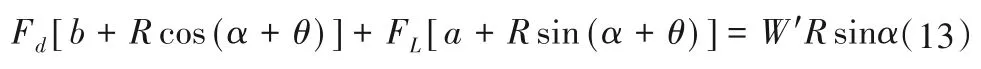
将式（6）～式（11）代入到式（13），并取a=b=R/3，化简后得：

式（14）中Gs为泥沙颗粒比重，令：

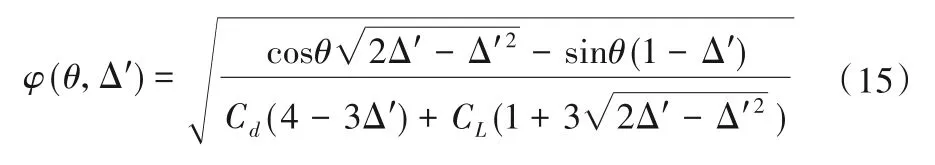
当Δ′取紧实排列时，考虑实际坡面流倾角多为0～30°之间，在此范围内验证可知，φ（θ，Δ′）随着坡度的增加，其值逐渐降低。而当θ取为定值时，一定范围内，φ（θ，Δ′）随着Δ′的增加而增大，将式（15）代到式（14）。则：

1.3 起动临界水深推导

为获取斜坡横断面上的流速分布，选取坡面径流条件下的水流剖面建立径流-渗流模型。如图3 所示，假设斜坡无限长，以水流方向为X轴正方向，垂直水流方向向上为Y轴正向，建立如图所示坐标系。坡面与水平方向夹角为θ，坡面长度为L，坡面径流沿Y轴方向水深为h，沿Y方向土层厚度为H，下部为基岩。沿X轴方向的流速为ux，坡内渗流流速沿X轴方向为vx，并忽略垂直渗流的影响。

图3 径流-渗流耦合模型Fig.3 Coupling model of runoff-seepage

针对所建径流-渗流耦合模型，采用文献［15］中水流的流速分布：

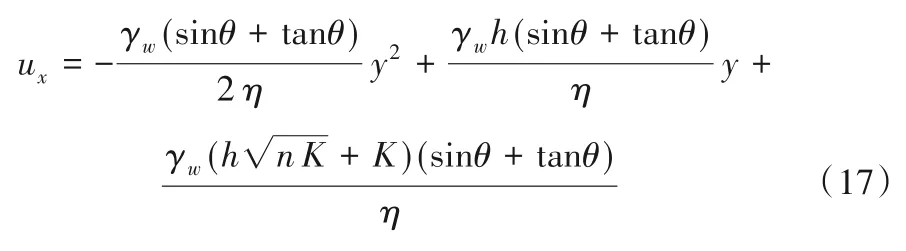
式中：γ w为水的容重；η为水的动力黏滞系数；n、K分别为坡面土体的孔隙率和渗透率；

由式（17）可知，令y=0即可得水流底部流速：

联立式（16）和式（18）即可得出径流条件下泥沙起动的临界水深：

由于渗透率K的量级较小，故式（19）右边第二项可忽略。同时，引入一个暴露度坡度因子λ（θ，Δ′），并令λ(θ，Δ')=式（19）可化为

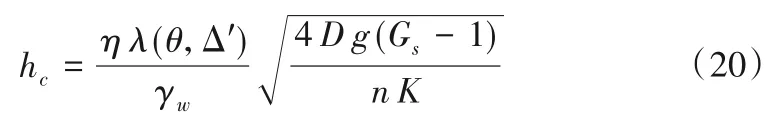
由式（20）可知，临界起动水深主要与颗粒粒径D、比重Gs、渗透率K、孔隙率n、斜坡坡度θ以及相对暴露度Δ′有关。理论表达式结合实际情况分析可得，θ一定时，一定范围内，当Δ′越大，其隐蔽作用越强，泥沙颗粒越不容易起动，故所需的临界水深值越大；Δ′一定时，在相应的坡度范围内，当坡度越大，重力分力对泥沙起动的影响就越大，相比之下，水流对泥沙的作用进一步削弱，故所需的临界水深较小。综上所述，斜坡上泥沙的起动主要与泥沙自身的物理性质、坡度还有相对暴露度相关。

2 公式验证

本文采用朱崇林等［10］的散粒体颗粒起动实测临界水深对式（20）进行验证。结果见表1 和图4～6。实验条件下每组粒径、每一坡度下分别测量了3 次，尽量避免了人为误差带来的影响。

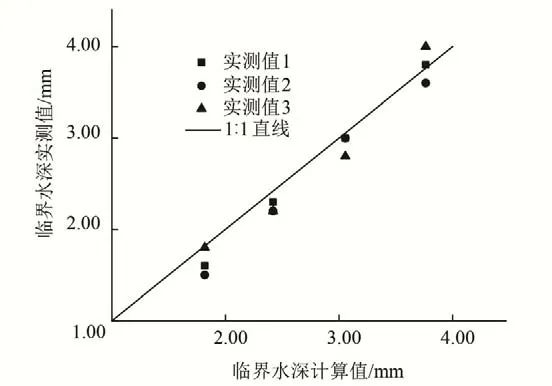
图4 粒径0～5 mm下临界水深计算值与实测值的比较Fig.4 Comparison between the calculated and measured values of critical water depth at 0～5 mm diameter

表1 斜坡临界起动水深计算值与实测值比较Tab.1 Comparison between calculated and measured values of critical starting water depth of slope

图5 粒径5～10 mm下临界水深计算值与实测值的比较Fig.5 Comparison between the calculated and measured values of critical water depth at 5～10 mm diameter

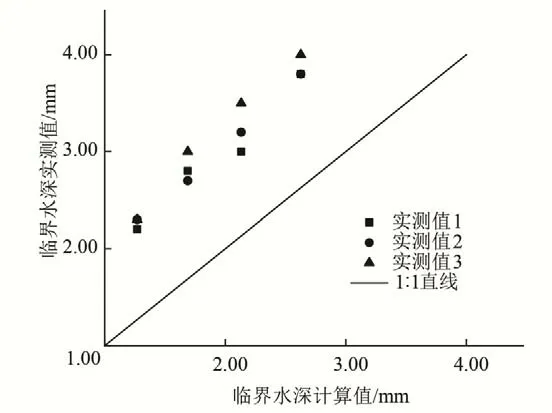
图6 粒径10～20 mm下临界水深计算值与实测值的比较Fig.6 Comparison between the calculated and measured values of critical water depth at 10～20 mm diameter

由表1 和图4～6 可以看出，随着坡度的增大，各粒组的相对误差值总体上呈现出增加的趋势。同时随着泥沙粒径的增加，同一坡度上的起动临界水深相对误差值也在逐步增大。在粒径5～10 和10～20 mm 之间，存在一个“分界粒径”，其值约为10 mm，在该粒径两侧的相对误差值存在一个显著的跃幅，整体相对误差大约上升31.23%。散粒体粒径在0～5 和5～10 mm 下，公式计算值与实测值相对误差不超过12%，最小为0.97%，精度较高；然而在粒径10～20 mm 下，二者的相对误差值开始显著增高，最高为44.10%。分析产生该结果的原因有：①泥沙的粒径较大，而此时的临界水深较浅，坡面上的水流无法完全覆盖泥沙颗粒，此时在水流作用下，水下重力大小、水流拖曳力和上举力的作用力大小及位置都有可能要发生改变；②由于实测数据的缺乏，在计算过程中，对散粒体泥沙进行了均匀沙处理，而大颗粒泥沙之间的嵌合能力更强，造成了其计算值比实测值偏低的结果；③在进行起动临界水深的推导过程中，令水流瞬时底速的边界条件取为y=0，可能对大颗粒泥沙起动的计算结果带来一定偏差。

综上所述，通过对计算值与实测值的比较，可以发现各粒组的相对误差值与坡度总体上呈现出正相关趋势。对同一坡度而言，起动临界水深相对误差值与泥沙粒径也呈现出正相关关系，存在一个“分界粒径”，超出此界限，相对误差值将显著增大。鉴于坡面薄层水流条件下的大颗粒泥沙受力较为复杂，对于泥沙粒径大于10 mm 的泥沙颗粒起动问题尚有待进一步研究。

3 结 论

在采用滚动模式推导斜坡泥沙起动临界条件的过程中，引入了相对暴露度的概念，并结合径流-渗流耦合模型下的流速分布，最终得到了斜坡上泥沙起动临界水深的理论表达式。该表达式表明临界水深的大小主要与泥沙自身的物理性质、坡度和相对暴露度有关。当Δ′取紧实排列时，表达式适用坡度范围为0～30°，此时临界起动水深与坡度呈负相关关系；当坡度取为定值时，在相应范围内，临界起动水深与相对暴露度Δ′呈一定的正向关系。实测资料表明该表达式对于粒径小于10 mm 的粒组的临界起动水深值预测较为符合，具有较好的精度。同时存在一个“分界粒径”，超出此粒径值，计算值与实测值二者的相对误差将显著增大。由于坡面薄层水流条件下大颗粒泥沙并不能被水流完全覆盖，受力情况和边界条件等较河道中的泥沙起动问题复杂得多，因此其起动问题尚有待进一步研究。