多系统融合单点定位先验和验后定权研究

张哲浩，潘林,2

(1.中南大学 地球科学与信息物理学院，长沙 410083；2.广西空间信息与测绘重点实验室，广西 桂林 541004)

0 引 言

全球卫星导航系统(GNSS)伪距单点定位具有算法简单、使用成本低、机动灵活等优点，广泛应用于民用导航等领域.随着北斗三号全球卫星导航系统(BDS-3)的正式开通，多系统融合已成为卫星导航定位技术应用的主流.相较于单系统，多系统组合可以显著增加可见卫星数量，改善卫星的几何分布，从而提高伪距单点定位精度及可靠性[1-2].

多系统组合定位时，由于各系统的星历精度、观测噪声不同，这会使观测值的精度存在系统性差异，从而导致随机模型难以精确构建.如何进行精确定权，是提高多系统伪距单点定位精度的关键问题.段举举等[3]利用Helmert 方差分量估计确定了GPS/GLONASS 组合伪距单点定位时两类观测值的权比(约为5∶1)，结果表明相比于GPS 或GLONASS 单系统伪距单点定位，双系统组合能使定位精度得到改善.何俊等[4]比较了等权模型、高度角模型、Helmert方差分量估计模型，GPS/GLONASS/北斗二号卫星导航系统(BDS-2)三系统组合伪距单点定位定位性能的差异，结果表明后两者模型定位精度明显优于等权模型，但二者差异不大.李文凯等[5]采用基于用户等效测距误差(UERE)的Helmert 方差分量估计模型，有效地提高了GPS/GLONASS/Galileo/BDS-2 四系统组合伪距单点定位精度.随着北斗卫星导航系统(BDS)的迅速发展，当前正处于BDS-2 向BDS-3 过渡阶段，BDS-2 与BDS-3 观测值共存.张乾坤等[6]针对二者的差异，对北斗单系统伪距单点定位随机模型进行优化，结果表明基于UERE 的Helmert 方差分量估计模型定位精度优于等权模型.

时至今日，随着各系统的现代化建设不断加快，GNSS 的观测精度已经有了较大提升，早些时期的结论可能不再适用.另一方面，尚没有多系统组合伪距单点定位随机模型的研究覆盖当前所有可用的GNSS星座.因此，需要对GPS/GLONASS/Galileo/BDS-2/BDS-3 组合伪距单点定位的随机模型进一步研究.本文将四大GNSS 系统的观测值划分为五类(BDS 分为BDS-2 和BDS-3)，分别采用高度角模型、UERE模型及基于二者的验后Helmert 方差分量估计模型进行四系统组合伪距单点定位，并对定位结果进行对比分析，以研究多系统组合伪距单点定位时构建随机模型的最优方法.

1 多系统组合伪距单点定位数学模型

1.1 函数模型

顾及各系统间时间基准的差异，将GPS 系统作为参考基准，对GLONASS、Galileo 与BDS 的基准统一后，四系统组合伪距单点定位观测方程[7-8]可表示为

1.2 随机模型

设同一历元内，各卫星观测值互不相关，且测量误差服从正态分布，则可得权阵

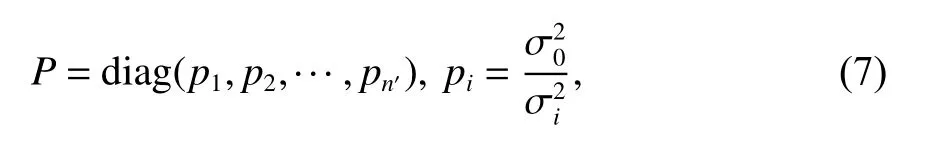
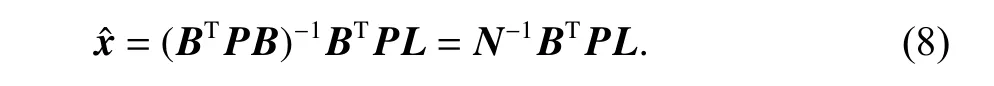
式中，N为法方程的系数矩阵.

由式(7)和式(8)可知，随机模型构建不合理将会影响定位精度.为探究最优的构建方法，本文选取了以下几种定权模型进行对比分析.

1.2.1 高度角模型

高度角可以间接反映卫星的观测值精度.当高度角较低时，观测值含有较大的大气层延迟及多路径效应误差，其精度较低，故可以根据高度角的大小确定观测值方差[9].高度角模型有很多种，本文采用正弦函数模型

式中：p、q为误差因子，本文取p=3 dm，q=3 dm；α 为高度角.基于高度角模型的定权公式为

1.2.2 UERE 模型

UERE 是与卫星及信号传播相关的各种误差源对伪距测量影响的综合反映[5-6]，其表达式为

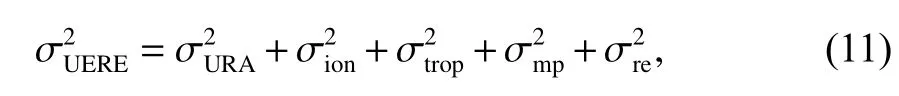
基于UERE 模型的定权公式为

1.2.3 Helmert 方差分量估计模型

实践证明，利用先验方差构建的随机模型一般是不够精确的，为了提高随机模型精度，可采用验后估计调整权阵[10].验后估计的方法很多，本文采用Helmert方差分量估计，将GPS 观测值分为第一类，GLONASS观测值分为第二类，Galileo 观测值分为第三类，BDS-2 观测值分为第四类，BDS-3 观测值分为第五类.

按上述分类原则，将式(2)重写为

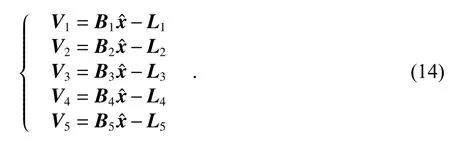
依先验模型定权及初次平差后，按Helmert 方差分量估计近似计算公式计算各类观测值单位权方差

式中：Pi为第i类观测值的权阵；ni为第i类观测值个数；解得单位权方差后，对各类观测值的权进行调整

Helmert 方差分量估计需迭代计算，其计算步骤如下：

1) 将观测值分类后，依据先验随机模型定权；

4) 反复进行第2)、第3)步，直至收敛.本文迭代终止条件为≤0.001，其中i、j=1,2,···,5 且i≠j.

2 实验与结果分析

2.1 实验数据

为了分析不同定权模型对四系统伪距单点定位精度的影响，本文在全球范围内选取了10 个多GNSS实验跟踪网MGEX(Multi-GNSS Experiment)观测站，其分布如图1 所示.各测站选取自2020 年4 月5 日至4 月11 日连续7 天的观测数据，采样率为30 s，截止高度角设为10°.所有测站数据均包含GPS、GLONASS、Galileo、BDS-2及BDS-3 观测值.

图1 2020 年4 月5 日至4 月11 日各MGEX 测站分布图

2.2 可见卫星数及PDOP 分析

表1 给出了各测站7 天平均可见卫星数及位置精度因子(PDOP)均值.从表中可知，GPS、GLONASS、Galileo 可见卫星数在全球范围内变化相对较小，分别为8～9 颗，5～7 颗，4～7 颗.相比之下，BDS 卫星数变化较大.当测站位于30°E～50°E 时，可观测到的BDS卫星数为8～17 颗，其中BDS-2 与BDS-3 分别为4～11 颗、5～8 颗(MIZU 站由于硬件原因仅能观测到1～3 颗BDS-3 卫星)，而当测站位于60°W～120°W时，由于无法观测到BDS 地球静止轨道(GEO)卫星与倾斜地球同步轨道(IGSO)卫星，其可见BDS卫星数下降至5～8 颗，其中BDS-2 与BDS-3 分别为0～2 颗、3～7 颗.从上述测站平均结果来看，各站单历元可见卫星数为31.9 颗，PDOP 值为1.0，这说明多系统组合能明显增加可见卫星数，并且基于更多的观测值能够提升卫星与用户间几何图形强度，降低PDOP 值.

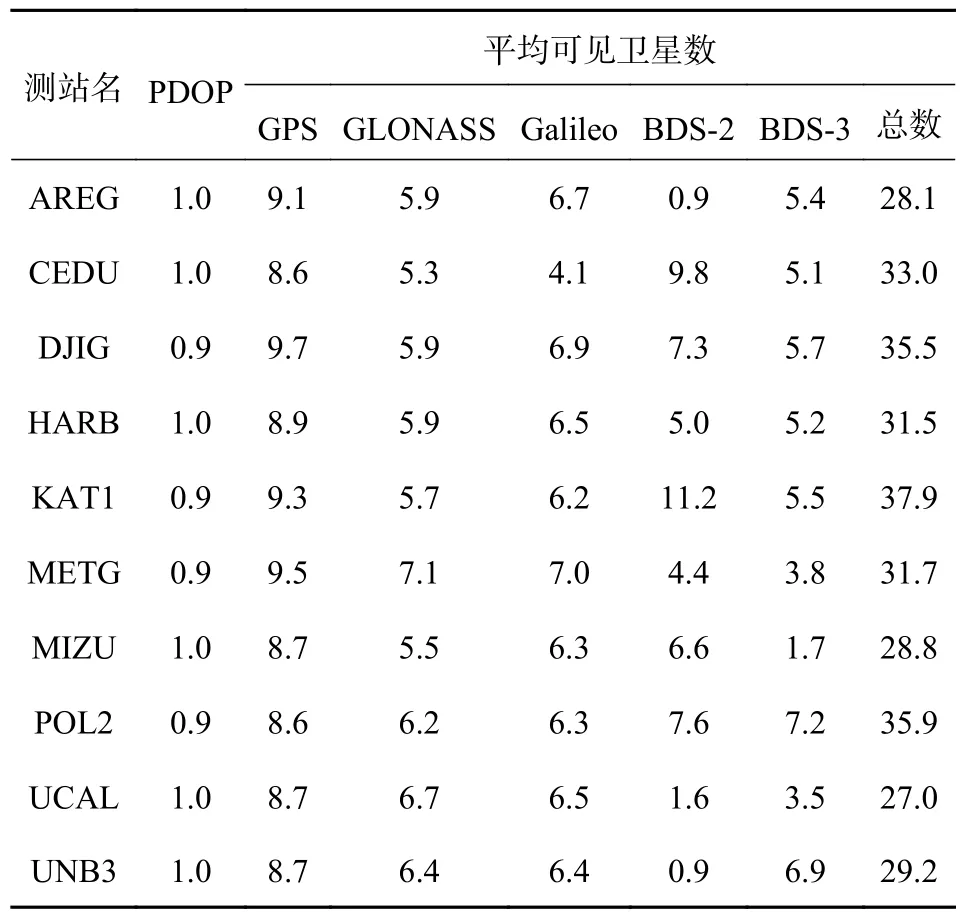
表1 各站7 天平均可见卫星数及PDOP 值

2.3 结果分析

分别采用高度角模型(ele)、UERE 模型(uere)、基于高度角的Helmert 模型(ele+hel)及基于UERE 的Helmert 模型(uere+hel)对各站7 天的观测数据进行解算.将解算结果与国际GNSS 服务(IGS)提供的测站坐标对比，计算各方向的定位误差.首先根据各测站单天定位误差序列计算均方根(RMS)统计值，然后对每个测站连续7 天的RMS 统计值取平均，结果如图2 所示.表2 进一步给出了各站的平均结果.

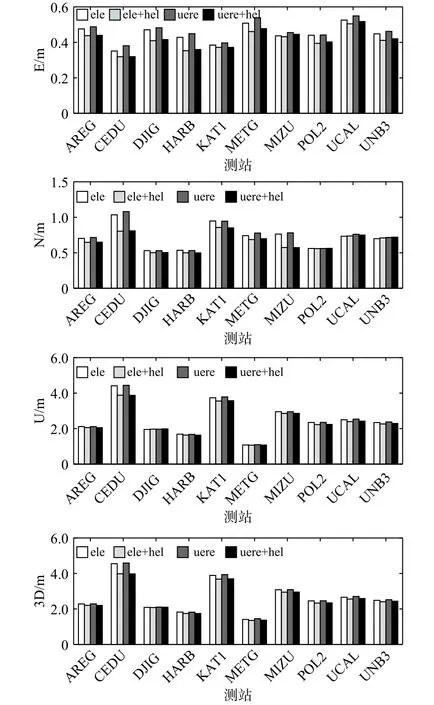
图2 各站7 天平均定位精度

表2 第三列与第五列括号中的百分数为Helmert方差分量估计模型相对于相应先验模型定位精度的改善率.由表2 及图2 可以看出，相较先验高度角模型，基于高度角的Helmert 模型定位精度在东(E)、北(N)、天(U)三方向上分别提高了4%～17%、6%～24%、2%～12%，在三维(3D)方向上，定位精度平均提高了0.143 m.相较先验UERE 模型，基于UERE的Helmert 模型定位精度在三个方向上分别提高了6%～20%、5%～27%、2%～12%，在3D 方向上，定位精度平均提高了0.155 m.以上结果说明，验后的Helmert 估计模型定权更为精确，其各方向的定位误差更小，能够更好地反映不同观测值之间的差异，从而提高伪距单点定位精度.

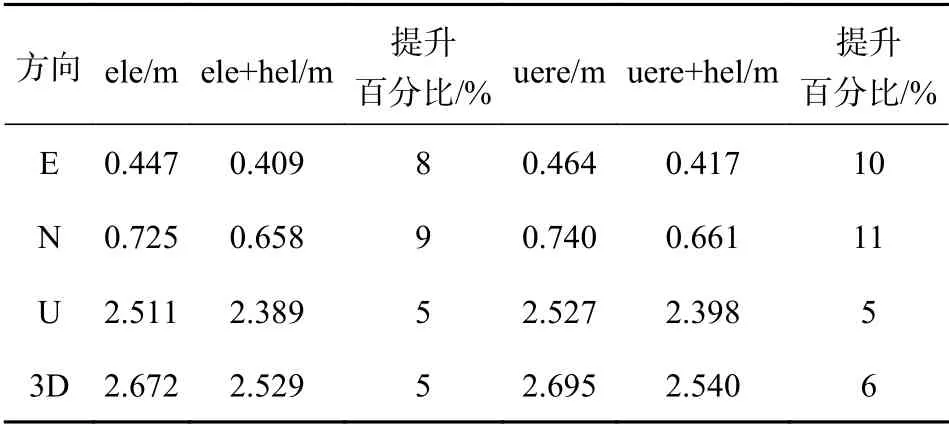
表2 不同定权模型平均定位精度对比

由于各测站所处的地理环境不同、各星座可见卫星数差异明显，这使得Helmert 方差分量估计后各站各方向的定位精度提升率也不同.由图1 及表1 可知，CEDU、KAT1 测站位于澳洲，能够观测到大量卫星，两站3D 方向的定位精度分别提升了约0.57 m和0.21 m.相对的，位于北美地区的UCAL 及UNB3站由于纬度高、可见卫星数较少(其中BDS-2 可见卫星数只有0～2 颗，远少于BDS-3 卫星)，在Helmert方差分量估计后，两站3D 方向的精度改善仅有几个厘米，并且在N 方向出现了略微变差的情况.故只有当卫星数量充足且星座间差异不大时，Helmert 方差分量估计才能够达到最佳性能.

进一步分析表2 可知，不同先验模型及验后模型间的解算精度也有不同.图3 展示了高度角模型较UERE 模型、基于高度角的Helmert 模型较基于UERE 的Helmert 模型在3D 方向定位精度的提升度(负值时表示精度降低).从图3 可以看出，对于大部分测站，高度角模型比UERE 模型定位精度提升了0.4～4.6 cm，平均提升2.3 cm，基于高度角的Helmert模型比基于UERE 的Helmert 模型定位精度提升了0.2～3.1 cm，平均提升1.1 cm.以上说明高度角模型优于UERE 模型，且基于高度角的Helmert 模型结果最优.

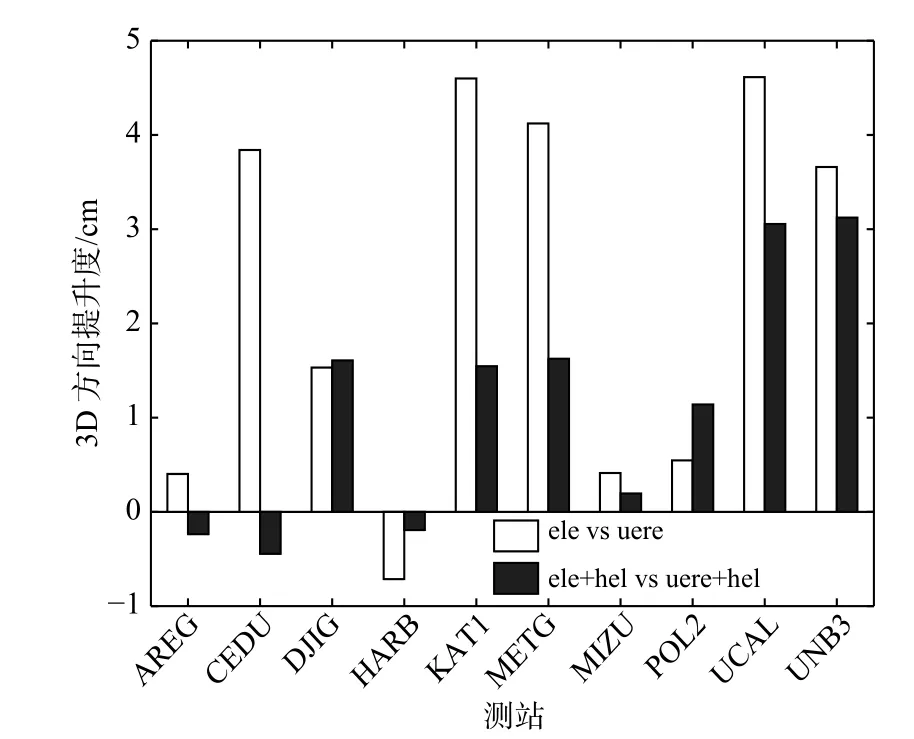
图3 先验及验后高度角模型相比于相应UERE 模型3D 方向定位精度提升度

出现上述现象的原因，可能是UERE 模型考虑的因素太多，削弱了高度角模型的优势.表3 给出了KAT1 测站在2020 年4 月5 日一天中部分卫星在不同时刻的观测值方差具体构成.从表中可以看出，UERE 模型主要由URA 及电离层误差决定，URA 是一些固定常数，电离层误差由模型计算所得，并不精确.计算UERE 时，由于二者与高度角误差相差一至两个数量级，在利用式(11)求和后削弱了高度角相关测量误差的贡献，因而影响了定位精度.部分低纬测站出现了UERE 模型更优的情况，但定位精度仅有约2～4 mm 的微小提升，并不明显.综上所述，建议在四系统融合伪距单点定位时采用基于高度角的Helmert 模型定权，以达到最优结果.

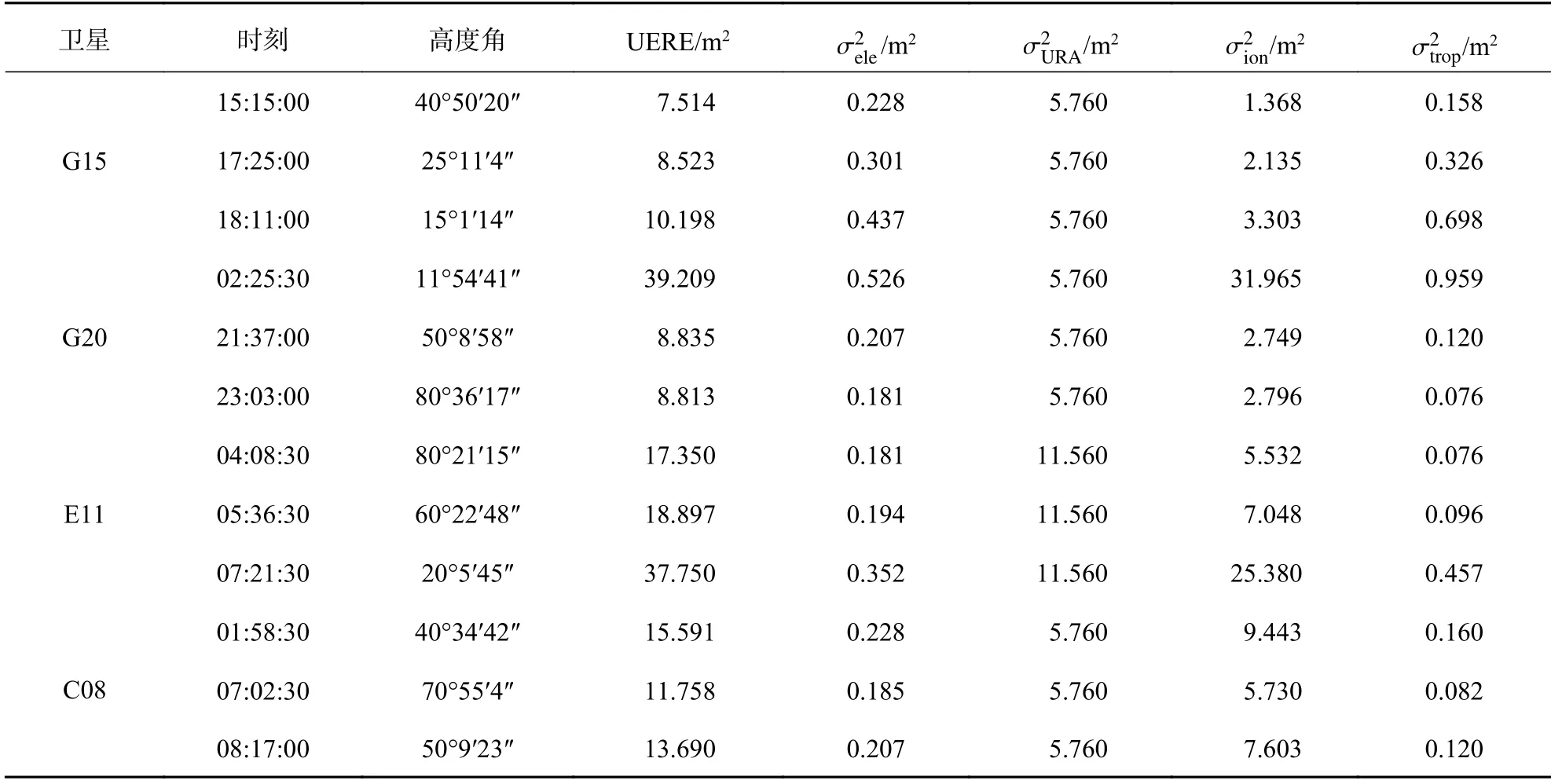
表3 UERE 模型观测值方差具体构成

3 结 论

本文聚焦于多系统融合伪距单点定位时随机模型的构建，将观测值分为了五大类(BDS 分为BDS-2 和BDS-3)，采用先验高度角模型、先验UERE 模型及基于二者的验后Helmert 方差分量估计模型，对10 个多GNSS 实验跟踪网MGEX 观测站连续7 天的观测数据进行解算，得出以下结论：

1) 与先验模型相比，验后Helmert 方差分量估计模型定权更合理、解算结果更优，3D 定位精度平均提升了15 cm.当卫星数足够多且星座间差异不大时，Helmert 方差分量估计模型能发挥最优性能.

2) 基于高度角模型的伪距单点定位定位结果优于UERE 模型，3D 定位精度约有2～3 cm 的提升，且基于高度角的Helmert 模型定位结果最优.