新零售产品的精准需求预测

2021-08-06张硕刘坤李希畅

中国集体经济 2021年19期

张硕　刘坤　李希畅

摘要：随着新的零售市场逐渐转型，生产模式指向多品种、小批量，商家的库存管理难度加大，若商家对消费者需求掌握不到位，可能会造成利润损失。文章研究的是新零售目标产品的精准需求预测问题，目的是使商家减少由于供大于求而导致的库存积压情况的发生，降低库存管理难度，获得更大的利润空间。此问题，文章参考了2020年第十届MathorCup高校数学建模挑战赛D题中的数据并进行处理。利用时间序列模型中的加权移动平均法和简单移动平均法从两个方面进行探讨：一方面，预测目标小类在2019年10月1日后三个月每个月的销售量，其中目标小类为历史销售时间处于2019年6月1日至2019年10月1日内且累计销售额排名前十的小类;另一方面，预测目标小类内所有skc（产品）在2019年10月1日后12周内每周的周销量，并给出每周预测值的MAPE。在这其中，假设市场环境良好，售卖商品均为合格品且售卖过程无意外。

关键词：时间序列模型;加权移动平均法;简单移动平均法

一、预测目标小类的月销量

在第一方面，我们运用到了时间序列模型中的加权移动平均法，先进行数据预处理，利用Excel将2019年7～12月的十个小类的销售量进行筛选加和，得出2019年7～12月十个小类每个小类每个月的销售量，然后使用Matlab根据加权移动平均法的知识，预测2019年10月1日以后未来三个月的销售量。

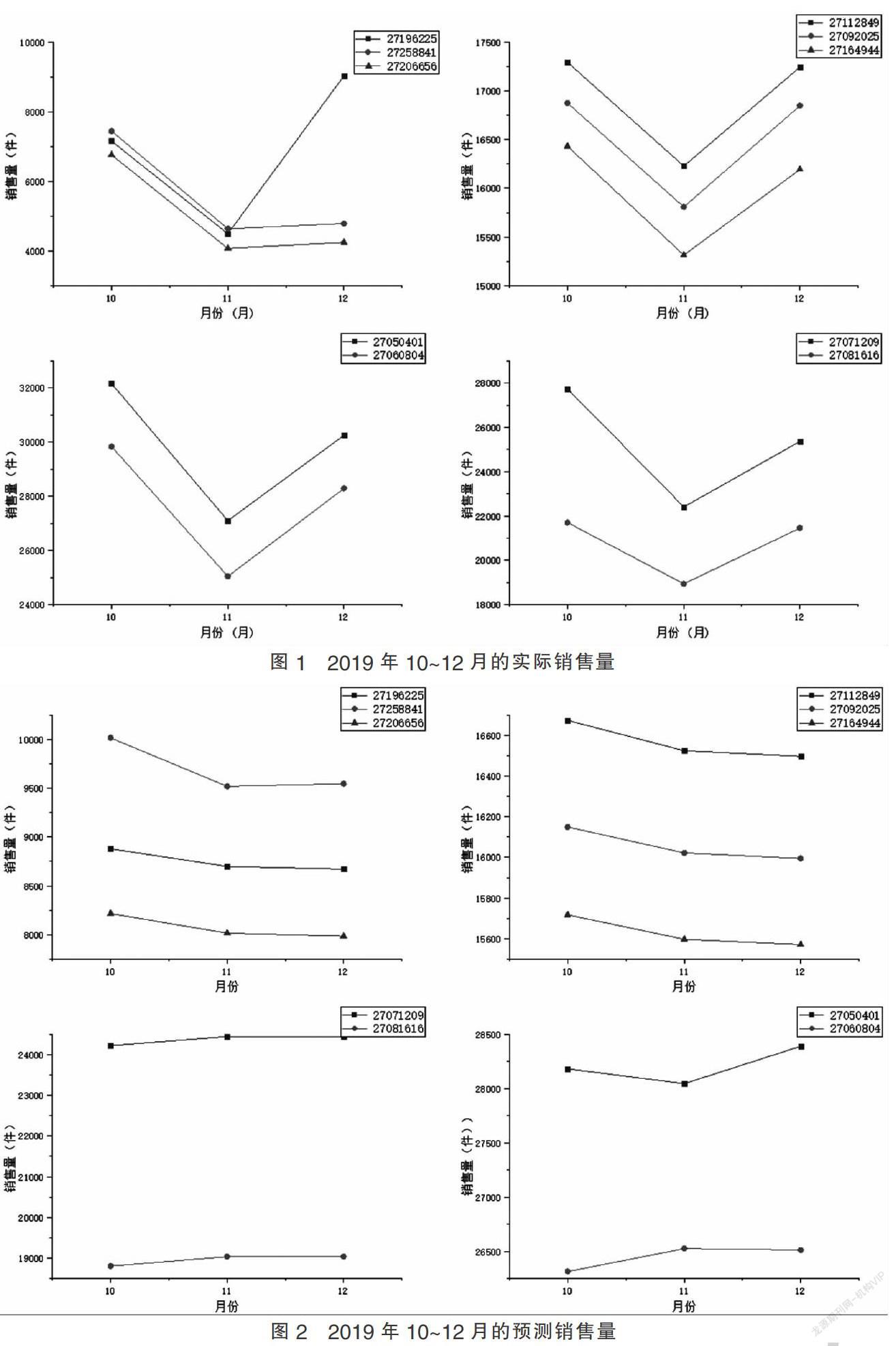
銷售额求出后，在十个小类中找出每个小类2019年7～12月的销售量。其中，求2019年7～9月的销售量的目的是通过预测模型的方法求出2019年10～12月的销售量的预测值，求2019年10～12月的实际销售量的目的是和预测销售量进行对比，并且为求对应的MAPE做准备。

找出2019年各小类7～9月的销售量后，以矩阵的形式存到Matlab中，利用Matlab结合时间序列模型中的加权移动平均法，计算出2019年各小类10～12月的预测销售量，然后计算出每个月的MAPE。

结合实际情况，预测2019年10月的销售量的时候，利用2019年7～9月份的实际销售量，以1：3：5的权重进行预测;预测2019年11月的销售量的时候，利用2019年8～9月份的实际销售量及10月份的预测销售量以1：3：5的权重进行预测;预测2019年12月的销售量的时候，利用2019年9月份的实际销售量以及10～11月份的预测销售量以1：3：5的权重进行预测。从而得出10～12月份这三个月的销售量预测值。

得出的MAPE值分别为10月：0.1428，11月：0.3210，12月：0.3219。

二、预测目标小类的周销量

主要运用时间序列模型中的简单移动平均法。把2019年10月1日前三周及后12周转换成日期，然后利用Excel按照问题一中得到的销量前十的小类分别找出对应的产品，以产品为桥梁，筛选出转换好的日期，进而求得每周的销量之和。然后利用Matlab结合时间序列模型中的简单移动平均法，找出2019年10月1日未来12周每周10个小类的周销售量，利用

式中yi表示2019年10月1日未来12周每周每个小类的实际销售量，y^i表示2019年10月1日未来12周每周每个小类的预测销售量，n表示小类个数。求出每周的所有小类的MAPE。

（一）简单移动平均法的原理

最近N期序列值的平均值作为未来各期的预测结果。一般N取值范围：5≤N≤200。当历史序列的基本趋势变化不大且序列中随机变动成分较多时，N的取值应较大一些。否则N的取值应小一些。再有确定的季节变动周期的资料中，移动平均的项数应取周期长度。选择最佳N值的一个有效方法是，比较若干模型的预测误差。预测标准误差最小者为好。

本研究是预测目标小类中所有skc在2019年10月1日后12周内每周的周销量，0设置N=3，利用2019年10月1日前三周每周的实际周销量，得出2019年10月1日后第一周的周销量，然后利用2019年10月1日前两周的实际周销售量和2019年10月1日后第一周的预测周销量的预测值预测出2019年10月1日后第二周的周销售量;利用2019年10月1日前一周的实际周销量和2019年10月1日后第一、二周的预测周销量预测出第三周的销售量。以此类推得出，2019年10月1日后12周的预测销售量。

得出的12周的周销量的预测值的MAPE为0.3157，0.6176，0.4396，0.4314，0.5695，0.2945，0.5987，0.7055，0.7326，0.6357，0.5297，0.6580。

（二）此方案的合理性

利用以下计算APE（百分比误差）的公式对第一方面的问题进行误差分析：

利用Matlab结合对应的数据（其中代表这个月各小类的实际销售量，y^i代表这个月各小类的预测销售量。）求得2019年10～12月每个月对应的十个目标小类的百分比误差APE，十月为0.1237，0.1269，0.2410;十一月为0.0399，0.0809，0.9762;十二月为0.0683，0.0450，0.0170。（鉴于APE数目较多，只取前三个目标小类的10～12月的百分比误差APE）

利用计算S（预测标准误差）的公式对第二方面的问题进行误差分析。

利用Matlab结合对应的数据（T=14，N=3，y^t是预测值，yt是真实值）求得十个目标小类的误差S，分别为：2208，2140，2140，1987，933，1987，2147，1987，3478，796。

利用时间序列模型中的加权移动平均法及简单移动平均法进行预测的销售量与实际销售量数据大致相同。

三、模型检验

（一）模型检验一

求解问题二用到的模型是时间序列模型中的加权移动平均法，以下是对于这个模型的检验：

利用百分比误差APE来检验实际数据与预测数据之间的差距。

利用Matlab结合相关数据求得相应APE的值，选取其中一个月（以10月为例）做出这十小类实际销售量与预测销售量的对比图中，二者数据基本重合。误差较小。

（二）模型检验二

利用预测标准误差S来检验实际数据与预测数据之间的差距。我们选取其中一周（以第六周为例）做出这十小类实际销售量与预测销售量的对比图中，二者数据基本重合。误差较小。

参考文献：

[1]汪国强.数学建模优秀案例选编（工科数学基地建设丛书）[D].广州：华南理工大学，1998.