基于模糊神经网络PID的塑料薄膜厚度智能控制
2021-08-06王楠
王 楠
(辽宁建筑职业学院,辽宁 辽阳 111000)
近年来,随着国民经济的快速发展,塑料薄膜在农业、工业、食品包装、医药等领域广泛应用,对塑料薄膜质量的要求也越来越严格,塑料薄膜厚度控制系统性能好坏直接影响薄膜质量[1-2]。塑料薄膜厚度受原材料质量、挤出温度和压力、拉伸速度等多种因素影响,是一个非线性、时变性、大时滞性的复杂系统[3-4]。薄膜厚度控制系统通常采用比例积分微分(PID)控制,随着薄膜厚度精度的提高,传统PID控制将很难达到理想的控制效果,同时传统PID控制由于参数固定不变,在应对复杂的薄膜厚度控制过程中无法根据实际情况对参数进行自适应调整。随着计算机技术和控制器芯片的快速发展,使许多复杂的智能控制算法能够在控制器中实现。如智能控制方法与PID控制相结合形成的控制方法,包括专家PID控制算法、模糊PID控制算法、神经网络PID控制算法以及基于粒子群PID控制等。智能控制算法克服了传统PID控制不足,可以根据系统情况对PID参数进行自动调节,改善了控制效果[5]。为了应对双向拉伸塑料薄膜厚度控制系统的非线性、时变性、大时滞性,本工作将模糊控制的模糊推理与神经网络的自我学习能力相结合,并用于传统的PID控制中,通过模糊神经网络控制实现PID参数的动态自整定。
1 双向拉伸塑料薄膜及其厚度控制系统
1.1 双向拉伸塑料薄膜结构
将塑料产品在一定温度条件下融化,并通过物理、化学、机械等方法将塑料进行横向和纵向拉伸,然后经过热成型、冷却处理以及胀紧等工艺,便可得到双向拉伸塑料薄膜。双向拉伸塑料薄膜生产线示意见图1,主要分为塑料融化挤出成型、纵向拉伸、横向拉伸、收卷4部分。塑料原料通过入料口进入挤出机,经过加热融化后由挤出机将其挤压到模头,通过挤出机的螺杆带动其挤出,经过冷却系统冷却后变为固体状厚片;厚片在传动系统的带动下,通过纵向拉伸,使厚片变薄,再经过横向拉伸使塑料薄膜进一步变薄变宽,最后通过定型收卷得到塑料薄膜成品。

图1 双向拉伸塑料薄膜生产线示意Fig.1 Process flow diagram of biaxially oriented plastic film
1.2 薄膜厚度控制系统结构
双向拉伸塑料薄膜厚度控制系统主要由电容式测厚传感器、微处理器(ARM)以及人机触摸屏组成,控制系统结构见图2[6]。塑料薄膜厚度是考察薄膜质量的重要指标,为了生产厚度均匀且达标的高质量薄膜,在薄膜生产过程中,需要使用非接触式、测厚精度高、数据传输快的测厚传感器。在薄膜生产线中通常采用测厚传感器A检测薄膜的横向厚度,测厚传感器B检测薄膜的纵向厚度,并将检测结果传送到ARM中进行智能PID计算,经过PID计算后输出控制信号,通过调整加热温度对薄膜横向厚度进行控制,调整冷却系统对薄膜纵向厚度进行控制。
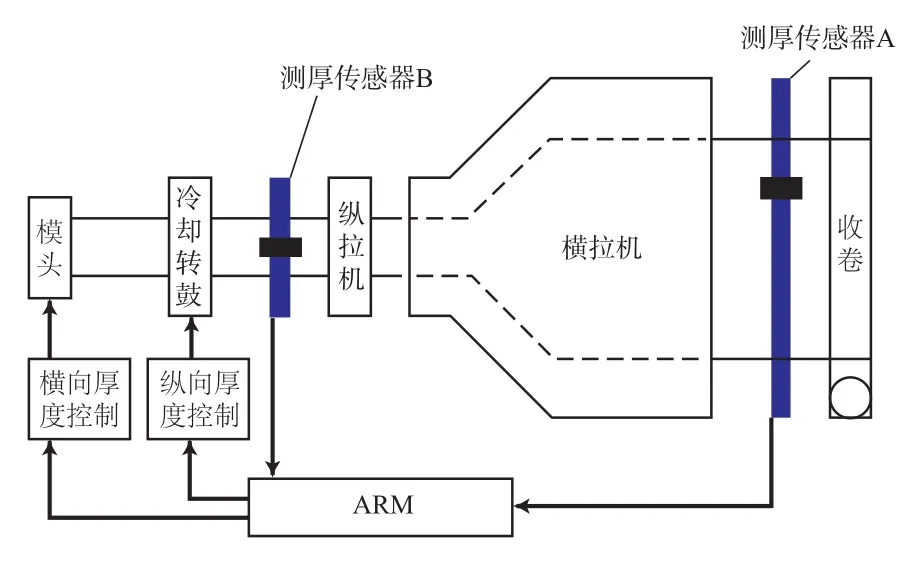
图2 双向拉伸塑料薄膜厚度控制系统结构示意Fig.2 Structure of thickness control system of biaxially oriented plastic film
2 PID控制
2.1 传统PID控制
传统PID控制主要通过采集测量值,将采集值与目标值之差作为系统输入,并不断地消除两者的差值。传统PID控制在实际应用过程中,通过选择适当的PID参数便可得到较好的静态指标,在工业控制领域被大量使用。在双向拉伸塑料薄膜厚度控制系统中,依据实际厚度与目标厚度之差,来调整PID控制器输出,传统PID控制器结构示意见图3。
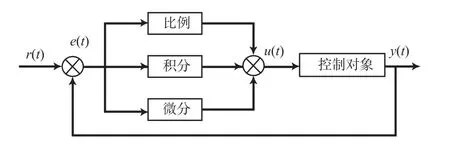
图3 传统PID控制器结构示意Fig.3 Traditional PID controller
传统PID控制的输入与输出之间的关系可以描述为式(1)~式(2)。

式中:Kp,Ki,Kd分别为PID控制的比例系数、积分系数、微分系数;t为时间。下同。
式(2)可以通过传递函数进行表达,得到式(3)。
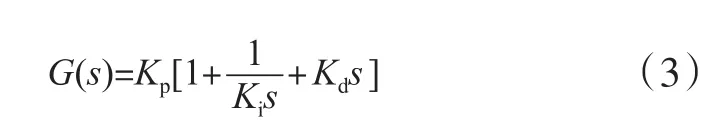
式中:G(s)为经过拉普拉斯变换;s是与式(2)中时刻t相对应的一个空间变量,并且整理后得到模拟PID调节器的传递函数。
2.2 模糊神经网络PID控制
塑料薄膜厚度控制是一个非线性、时变性、大时滞性的复杂系统,传统的PID控制由于其控制参数是固定不变的,不能根据系统的变化对参数进行自适应调整,薄膜厚度控制效果并不理想[7-9]。因此,将模糊控制理论与神经网络的自我学习能力相结合,并用于传统PID控制中Kp,Ki,Kd的自适应调整,从而提高系统的收敛速度,增强系统的抗干扰能力。模糊神经网络PID控制器结构示意见图4。
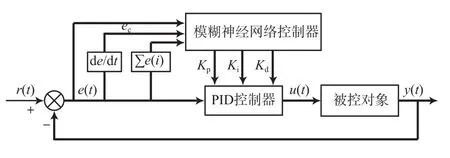
图4 模糊神经网络PID控制器结构示意Fig.4 Fuzzy neural network PID controller
模糊神经网络控制器主要由输入层、模糊层、模糊推理层和输出层组成。薄膜厚度误差为神经网络输入层中的输入量,薄膜厚度误差变化率以及误差累积量可以用输入层激活函数[见式(4)]表示。

其中,输入可表示为式(5)。

选用高斯函数作为激活函数,见式(6)。

式中:i=1,2,3;j=1,2,3,4,5,6,7;mij表示第i个输入量的第j个模糊集隶属度函数的均差;σij表示标准差。
模糊神经网络控制器中推理层同样包含7个神经元,各神经元分别对应一个模糊规则,所述7个神经元分别对应模糊集内部的{NB,NM,NS,Z,PS,PM,PB},即负大、负中、负小、零、正小、正中、正大。可将已模糊化处理的输入量两两相乘,进而得到该层输出值。所以该层激活函数可表示为式(7)。
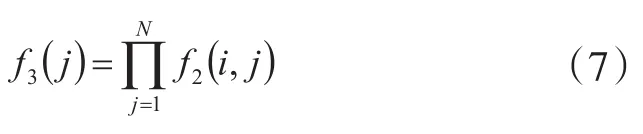
模糊神经网络输出层的输出分别对应PID控制器的3个参数Kp,Ki,Kd。定义连接权矩阵为w,经过模糊神经网络推导可以得到PID控制器新的参数,见式(8)。

3 仿真分析
为了验证提出的模糊神经网络PID双向拉伸塑料薄膜厚度控制算法的有效性,本工作采用Matlab仿真软件进行了仿真分析。薄膜厚度数学模型见式(9)。

为了比较传统PID控制、模糊PID控制以及模糊神经网络PID控制算法的性能,对双向拉伸塑料薄膜厚度控制系统进行单位阶跃响应仿真分析,从图5可以看出:与传统PID控制和模糊PID控制相比,模糊神经网络PID控制算法具有更加优良的动静态性能,超调量基本为0,稳态误差为0,上升时间为1.84 s,调节时间为2.10 s,由此可以看出,采用模糊神经网络PID控制能够显著提高薄膜厚度控制精度。
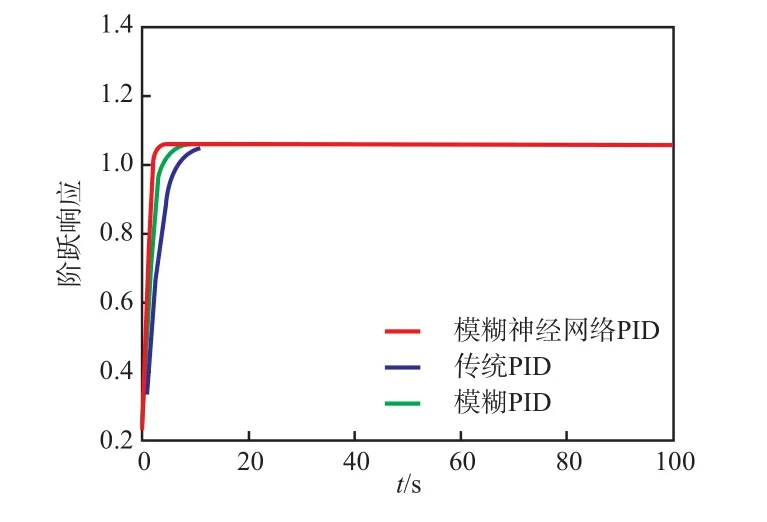
图5 单位阶跃响应仿真曲线Fig.5 Simulation curves of unit step response
双向拉伸塑料薄膜在实际生产过程中,存在许多外部干扰因素,为了验证文中算法在抗干扰能力方面的性能,在图5的单位阶跃曲线仿真分析中,在50 s时引入阶跃响应干扰因素,从图6可以看出:模糊神经网络PID控制算法能够快速地克服外部干扰,并且该算法能够以较快的速度达到稳定。
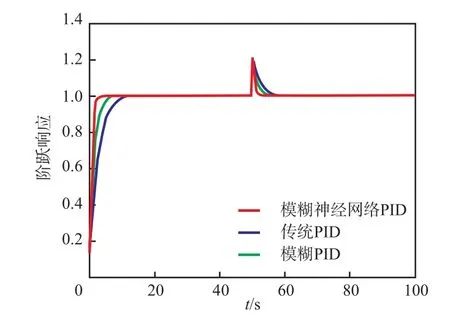
图6 抗干扰能力仿真曲线Fig.6 Simulation curves of anti-interference
4 结论
a)结合模糊控制、神经网络控制和PID控制,设计了一种模糊神经网络PID控制方法。
b)仿真结果表明,模糊神经网络PID控制算法较传统PID控制与模糊PID控制具有更加优良的控制性能(如超调量小、稳定周期短、精度高、抗干扰能力强),该控制算法对于提升薄膜质量具有重要作用。
