双排桩在水利工程深基坑支护中的应用

黎子荣

(深圳市广汇源环境水务有限公司,广东 深圳 518000)

1 双排桩相关概述

双排桩支护技术是沿着基坑的侧壁设置前后两排梁、支护桩所连接而成的冠梁以及刚架支挡结构。双排桩结构主要是针对在工程中保持总桩数不变情况下，把传统单排悬臂桩部分桩柱进行后撤，设置成排桩对应、梅花式结构。根据相关研究报告显示，双排桩结构具有位移小、刚度大，受力合理的特点，相比于单排桩有形式特点，并且桩顶上通过连梁将前后排桩进行相互连接构成空间结构，实现更大程度的支护。双排桩结构中较为常见的包括丁字式、之字式、连梁式、三角式、矩形结构式、梅花式。连梁的形式通过不断研究实践也形成多样化，其中常见的连梁形式包括盖板式、斜撑式、深梁式、腰梁式。经过大量的工程实际表明，连梁形式的不同其刚度也存在一定的差异，在双排桩结构中连梁的刚度对其整体性能存在直接的影响。在实际的项目工程中需要按照实际情况和具体要求对连梁形式进行合理的选择，保障双排桩结构具有足够的安全性、可靠性。

2 双排桩结构的计算模型

通过大量实验和工程实践应用，对双排桩结构计算分析时，其计量模型分为基于土拱理论、Win-kle假定、经典土压力三类。从实践应用效果和经验方面看，土拱理论和Win-kle假定两种方式在进行模型计算是对土与桩之间共同作用加以考虑，因此其结果较为准确、贴合实际，在工程项目中较为常见的模型包括两种：平面刚架模型和平面秆系有限元模型。就两个模型来说，双排桩通过和刚性连梁把前后桩排构成超静定结构，确保整体结构具有良好的刚度。换句话说，双排桩如同将刚架深深插入土基中，通过利用基坑以下来自桩前土的被动土压力作用与钢架插入土中部分前后的桩抗压、拔作用所生成的力偶，使之间形成合力而平衡力矩，通过桩土之间相互作用减少双排桩水平位移和桩内力。

通过以上作用来看，双排桩结构在多变复杂的荷载作用中可以自动调整自身内力，确保结构能够更加良好地适应复杂或者难以计算荷载条件的项目中。图1为考虑到桩土相互之间作用平面杆系有限元模型，通过该模型对双排桩工作性状进行科学模拟。

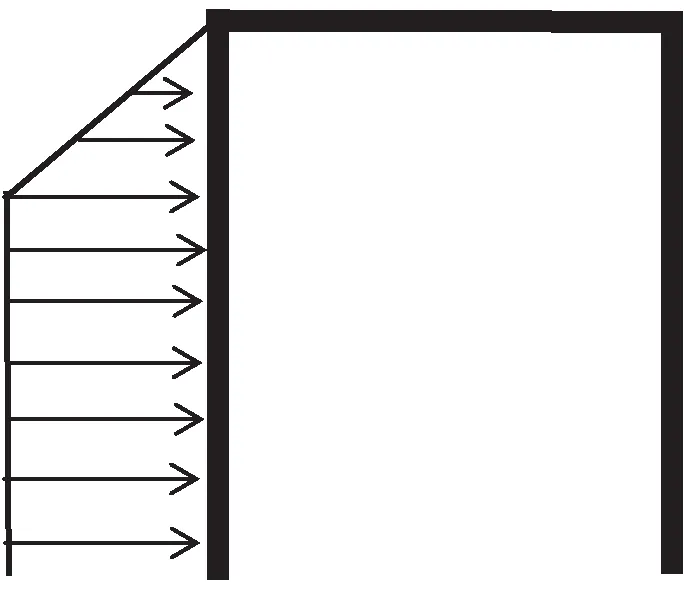
图1 平面杆系有限元模型图

当受到荷载作用时，双排桩将会向基坑内进行运动，造成后排桩桩底和土体产生脱离，桩底不存在约束作用；在此条件基础上，桩柱之间作用主要表现在后排桩存在抗力作用，前排桩受到推力作用，对桩间土和前排、后排桩之间作用力的方向加以考虑，为水平方向作用力。所以可通过应用弹簧进行等效模拟桩间的土体，实现前后排的有效连接，土体间压力分配相当于通过双排桩和弹簧之间位置进行协调实现。通过模拟分析，应用弹性地基梁方式和结构力学能够将双排桩结构内力值加以准确地计算。在实际的工程项目中平面杆系有限元模型较为适用，对于桩顶位移的计算和实测结果较为相近。

3 双排桩结构优点

通过大量的实践应用表明，相比于单排桩，双排桩具有以下四方面优点。首先，单排悬臂作用机制是完全源自被动区土体土抗力，通过土抗力实现对侧压力的平衡，进而形成较为稳定的结构，但是桩顶具有较大的位移，相比双排桩结构通过使用连梁将前后排桩进行刚性连接来讲，不仅整体较为稳定，位移量较小，同时具有足够的刚度。其次，就作用机理而言，前后排桩和桩间土共同作用，产生力偶的方向和侧向力方向相反，当处于多变复杂外荷载情况下，能够用自身内力进行有效调整，具有更为良好的适应性，桩内力较小能够有效减少桩顶的位移。再次，双排桩通过连梁进行连接能够对双排桩内力特征和变形加以调整，避免结构出现位移，对正负弯矩进行调整，减少桩身配筋的使用量，降低工程造价。最后，双排桩能够替代桩锚支护形式，避免对挡土侧建筑地基、管线等重要构筑物造成破坏，施工工艺较为简便，施工速度快，能够有效缩短工期。

4 双排桩结构在深基坑支护中的应用案例分析

4.1 工程概况

该工程为水闸，主要作用是防御台风、同时具备通航、排洪、排涝作用。在水闸底层有比较厚的淤泥层，对于水闸底板的设计埋深较大，在闸址的右岸分布有厂房，需要进行深基坑支护。基坑的开挖深度比较深，需要开挖深是这8.50 m，在支护顶之上存在高岸坡，高为4.90 m。对于深基坑的防护选择双排桩方式。在2011年基坑降水时，厂房出现开裂、沉降等情况，因为支护的安全性对工程存在较大影响。另外，为保证水闸工程的顺利开展，应当在基坑开挖后对支护结构安全性进行复核。

4.2 项目地质情况

项目工程位于三角洲西部，因为受到潮汐影响，河水的水位存在较大的变化。闸址内地层主要为第四系地层，分别为人工填土层，该层主要是路基土，以煤渣、中粗砂、碎石土为主要成分，另外还存在粉细砂和黏性土。3.00～5.10 m厚，标贯击数为5击，下层为海陆交互相沉积层，多是灰黑色的淤泥，少部分是淤泥质黏土，9.50～26.90 m厚，平均为16.20 m，标贯击数<1。通过勘测显示抗剪强度建议值φq为4°～5°，Cq为3～5 kPa，之后经过岸坡稳定确定φq为5°，Cq为7 kPa。在此下层为全风化花岗岩，风化情况较为完全，呈现为粉质砂质黏土状，少部分为岩碎块，底部较为坚硬，标贯击数为28，按照有关公式计算得出φq为24°，Cq为40 kPa。

4.3 对比分析正双排桩程序和有限元MIDAS/GTS程序

首先确定计算方法对正双排桩程序和有限元MIDAS/GTS程序进行计算。经过对比选择较为合理的计算方式，通过“m”法进行计算，桩前被动范围通过弹性支点进行支撑，按照理正程序，极端理论模型如图2。

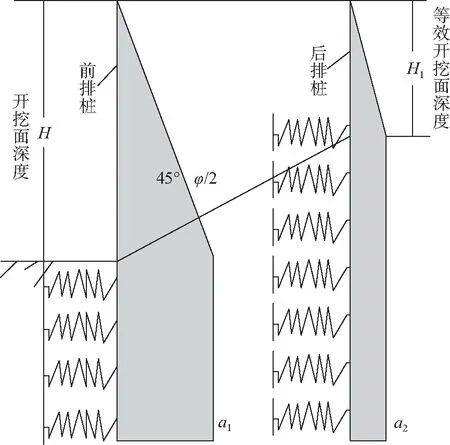
图2 计算理论模型图

其中a1、a2表示为前排桩与后排桩土压力的分担系数，在进行计算时a1取1、a2取0，由前排桩对全部的土压力进行承担。通过MIDAS/GTS程序计算有限元，双排桩通过梁单元进行模拟。按照土层的实际情况将主动土的压力作为外荷载施加至前排桩，刚度按照“m”法进行计算，对于支点刚度的计算按照KS=mb0(z-hn)进行计算。应用两种方式进行计算时需要确保边界条件一致，在进行计算时选择简单模型，计算断面为取闸室段，开挖深度8.50 m，嵌固深度为10 m，对支护顶以上土体和超载情况不给予考虑，计算模型如图3所示。

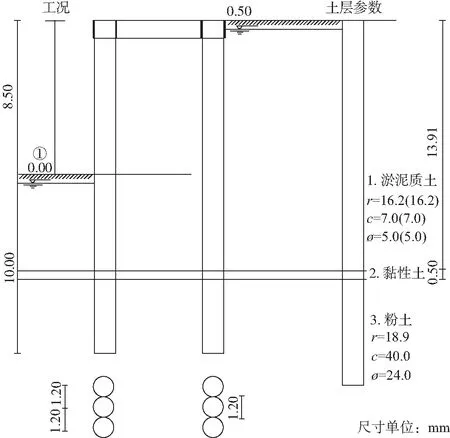
图3 计算模型简图

之后对比计算结果，理正双排桩的计算结果为最大弯矩1 515 kN·m，最大位移35 mm。有限元程度进行计算最大弯矩1 576 kN·m，最大位移32 mm。通过对比计算结果能够发现：当边界条件一致时，通过以上两种方式进行计算其结果较为接近，因此通过理正程序进行计算具有一定的可靠性，因为考虑理正程序计算方式较为简单，因此选用该方式进行计算。

4.4 断面计算和土压力分担系数影响分析

通过理正程序法对支护结构处于不同分担系数情况下的弯矩与位移进行计算，计算结果如表1所示。

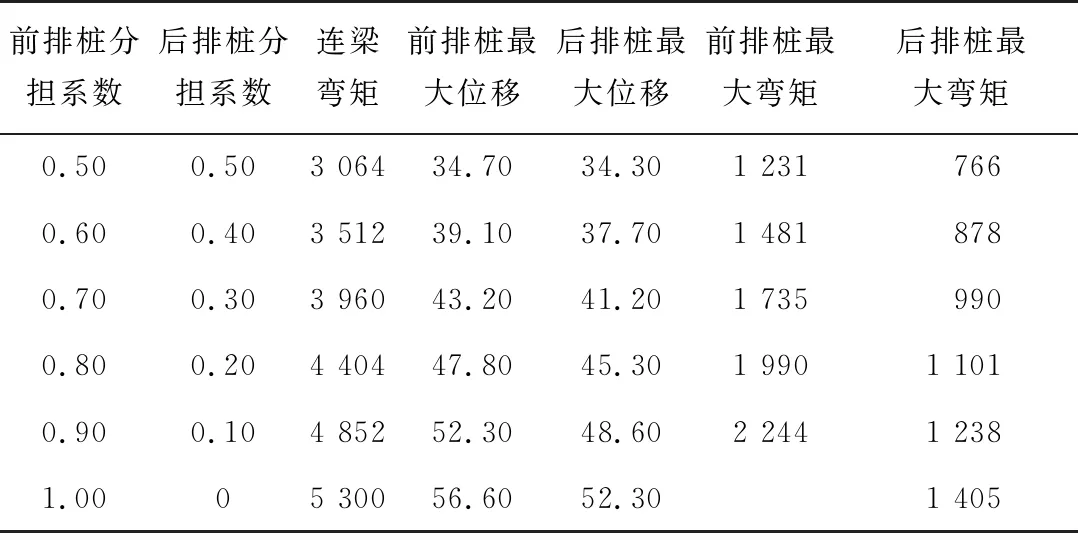
表1 不同分担系数双排桩位移和弯矩表

通过以上分析可以得出分担系数的变化对双排桩结构的位移和弯矩存在较大的影响，当前排桩的分担系数降低，后排桩的分担系数提升时，两者位移、弯矩以及连梁所受的弯矩都降。之后取消后排桩进行结构计算，然后对数据进行分析，当前排桩的分担系数固定时，后排桩分担土压力与否，对前排桩弯矩具有较小的影响，后排桩所受弯矩较大。通过分析土压力降低50%，模型移位、弯矩存在较小的变化。

5 总结

在非闭合基坑中难以采用传统的支撑体系，在水利工程中往往基坑较深，采用传统的支撑方式难以达到技术要求标准，而通过应用双排桩结构能够有效达到支护要求。另外双排桩结构的应用能够降低对基坑周围环境影响，具有操作简单、施工速度快，经济效益较高的特点。