Butterfly网络的置换理论研究*

吴朋庭，李 军，何卫国，王明东

（成都三零嘉微电子有限公司，四川 成都 610041）

0 引 言

Butterfly网络广泛应用于比特扩散、比特循环移位等动态比特置换运算模块的硬件实现。以往的研究主要集中于挖掘其数据通路的递归特性[1-6]。例如，比特扩散运算。在每一层置换参数求解的过程中，Lee发现了一些Butterfly置换网络的递归特性，并利用这些特性对部分运算过程进行了简化[1]。简化的过程非常精妙甚至有些偶然，然而在数学的世界里面，偶然现象一定存在其必然的数学理论。所以，无论研究人员归纳出的Butterfly置换网络结构的递归特性多么精妙，都是建立在它的数学理论基础之上的衍生特征。只要充分利用其数学理论对运算进行推导，就可能获得优化程度不低于现有递归算法的方案。

本文旨在研究Butterfly网络的置换数学理论及其应用。首先采用数字与符号对Butterfly网络结构进行定义，其次利用这些定义总结归纳Butterfly网络结构的数学理论并予以证明，最后利用Butterfly网络的数学理论重新分析比特扩散和循环移位等特殊的置换运算，以期得到优化程度更好的硬件实现方案或者更加简单的置换参数求解过程，为研究人员进一步分析其他置换运算提供新的思路。

1 Butterfly网络的数学理论

图1为一个Butterfly置换网络结构，N（N=2n）比特数据对应的Butterfly置换网络的宽度为N，路由深度为n。

为了描述它的结构特征，需要引入一些定义。

原始数据从右到左第jn比特称为起点s(jn)，目标数据从右到左第j0比特称为终点e(j0)，中间第i层数据从右到左第ji比特称为路由点r(i,ji)，第i+1层路由点r(i+1,ji+1)到第i层路由点r(i,ji)之间的路线称为路由线l(i,ji+1→ji)，路由线l(i,ji+1→ji)在横坐标上投影的最大距离称为路由权重w(i)，且w(i)=2i。

以权重w(i)为宽度，第i层数据被划分的2n-i个区间称为路由区间 b(i,k)=[(k+1)×2i-1,k×2i]，(0≤k≤2n-i-1)。当k为奇数时，b(i,k)为奇区间ob(i,k)；当k为偶数时，b(i,k)为偶区间eb(i,k)。路由线l(i,ji+1→ji)从上而下划过的方向在横坐标上的投影称为路由方向d(i,ji+1→ji)，且当ji∈ob(i,k)时 d(i,ji+1→ji)∈ {0,1}，当 ji∈ eb(i,k)时 d(i,ji+1→ji)∈{-1,0}，其中“1”“-1”“0”分别表示向左、向右和保持。

从起点s(jn)出发，途经各层路由点r(i,ji)并最终到达终点e(j0)划过的所有路由线l(i,ji+1→ji)的首尾相连的组合称为s(jn)到r(i,ji)的路由路径p(jn,j0)。将路由路径经过的所有路由点对应的路由方向剥离符号后得到的元素d[i]组成路由向量d={d[n-1],d[n-2],…,d[1],d[0]}。

综上所述，存在以下路由等式：

由于位移主要发生在横坐标上，仅考虑横坐标上的投影，则有：

定理1从任一起点s(jn)出发到任一终点e(j0)的路由路径仅有一条。

证明：假设从起点s(jn)出发到任一终点e(j0)的路由路径有两条，则有：

由于两条路由路径的终点相等，那么这两条路径在终点或者终点之前必定存在一个交点，且在此之后汇聚成一条路径。

假设交点存在于第t层，则有：

由于两条路径在路由点r(t,jt)处汇聚，因此d2(t)≠ d1(t)。

当 r(t,jt)∈ ob(i,k)时，d2(t)、d1(t)∈ {0,1}， 则|d2(t)-d1(t)|=1。

当 r(t,jt)∈ eb(i,k)时，d2(t)、d1(t)∈ {-1,0}，则|d2(t)-d1(t)|=1。

因此，有：

等式的左侧为偶数，等式的右侧为奇数，产生矛盾，定理1得证。

定理2任一起点s(jn)出发到任一终点e(j0)的路由传递过程是两点横坐标的异或运算。

证明：将起点s(jn)和终点e(j0)的横坐标做二进制数展开，得：

根据式（2），有：

根据定理1，有：

当j0[i]=1时，表示路由点落在第i层的奇区间，d(i)的符号为“+”，有：

当j0[i]=0时，表示路由点落在第i层的偶区间，d(i)的符号为“-”，有：

对于不含进位的单比特加减法，有：

因此，定理2得证。

由于Butterfly置换网络的数学理论本质就是初始坐标与目标坐标的二进制展开式的按位异或运算。因此，只要知道输入数据的初始坐标和目标坐标，就能通过异或运算快速得到该数据的路由向量d，从而为求解Butterfly置换参数做好准备。

如图2所示，初始坐标为“5”和“3”的数据需要通过Butterfly网络分别置换到“2”和“5”的目标位置。它的各层置换参数与路由向量元素的数值相等，位置正好处于各层的路由点r(i,ji)上。

因此，求出路由路径各层路由点的横坐标就能快速得到Butterfly网络的置换参数。根据路由路径的定义和异或运算的交换特性，可得递归算法：

由于已知终点e(j0)，因此可以选择从终点横坐标j0出发逐层推导出路径上各路由点的横坐标ji，然后将各层的路由元素放置到该位置，得到置换参数。

综上所述，如图3所示，求解某置换运算的Butterfly置换参数的算法步骤可以分解为：

（1）根据已知条件求解数据的起始地址；

（2）根据已知条件求解数据的目标地址；

（3）初始地址和目标地址异或得到路由向量集合，设置i=0；

（4）使用路由向量第i层元素d[i],，修正其上所有层路由向量元素d[i+1]～d[n-1]的位置，i++；

（5）重复步骤（4）直到i=n-1，即得到Butterfly置换参数。

可以选择目标地址为参照坐标系，由此合并步骤（1）和步骤（2），调整为根据已知条件求解目标地址上数据来源的起始地址。

2 Butterfly网络数学理论的应用

2.1 PDEP运算

如图4所示，PDEP运算是一种比特扩散运算。它根据置换掩码数据中“1”的数量m，选中输入数据最低m比特数据，然后将选中的这些数据从右至左第j比特移位到掩码数据中从右至左第j个“1”对应的位置上，0≤j≤m-1。

Lee等人发表的论文证明了PDEP运算可以采用Butterfly置换网络结构实现，并提出了置换递归算法来对置换参数进行求解。

整个求解过程在硬件实现时被分解为3个步骤：

（1）计算置换掩码mask在位置区间[j,0]，(0≤j≤N-1）中“1”的数量 POPCNT(mask[ j:0])；

（2）在第i行，对k(i)=2i个“1”执行LROT C(1k(i),POPCNT[mask[(2t+1)×k(i)-1:0])]运 算 ，其 中0 ≤ i≤ log2N-1，0 ≤t≤ 2n-i-1；

（3）将（2）中计算的结果按照左对齐的方式放在第i行第(2t+1)×k(i)-1列的位置，从而得到完整的置换参数[1]。

作为对比，本文采用第一章提出的Butterfly网络的置换数学理论对PDEP运算的置换参数求解过程进行推导。

为了方便描述，以下采用8 bit PDEP运算进行分析，如图5所示。

根据Butterfly置换网络数学理论求解置换参数的标准流程如下。

（1）根据已知条件求解各目标位置上数据的起始位置。该运算的已知条件包括置换掩码和输入数据，输入数据作为被置换的对象，本身并不包含任何位置信息，因此可以利用的已知条件只有置换掩码。

PDEP运算的定义是将输入数据从右至左的第js比特din[js]置换到输出数据中对应置换掩码从右至左的第js个“1”的位置上。把定义反向推导即可得知，置换到输出数据第je比特dout[je]的数据来源是置换掩码mask[je]对应位置的“1”是其从右至左的第几个“1”，也就是mask[je]对应位置的“1”在整个置换掩码中的编号。

如图6所示，置换掩码从右至左第1个“1”编号为0，因此其je位置上的“1”的编号是je位置右边所有“1”的数量和，即POPCNT(mask[ je:0])。所以，比特扩散的输出有效位，对应的数据来源位置即为POPCNT(mask[ je:0])。由于其他非扩散有效位的数据在输出时将统一被置换掩码过滤为“0”，其运算中间结果是多少并不重要。为了简化运算，可以与有效位的数据来源算法保持一致。

综上所述，目标位置je上数据的起始位置求解算法为POPCNT(mask[ je:0])。

（2）初始排序和目标排序异或得到路由向量集合。根据（1）中的算法，可以计算得到N比特PDEP运算输出数据的初始排序为：

只需将其与目标排序{N-1,N-2,…,2,1,0}做异或操作，就可以得到Butterfly网络的路由向量集合，如图7所示。

（3）对路由向量集合进行修正得到置换参数。该步骤的一般处理办法是利用路由向量集合中第i层的元素，对第i+1层到第n-1层的元素进行置换修正，然而将额外引入一个Butterfly网络的硬件开销，也没有进一步优化运算复杂度，不符合利用Butterfly置换网络数学理论求解问题的预期。正确的做法是进一步挖掘置换的本质就是异或带来的运算特性，如图8所示。

从步骤（1）化简后的PDEP运算结果可以发现，第i层奇区间eb(i,2k+1)和偶区间ob(i,2k)中的对应路由点的起始位置js1和js2相差小于等于2i，因此两个起始位置的二进制展开式在第i层的组合(js1[i],js2[i])可能有 4种情况——(0,0)、(0,1)、(1,0)和(1,1)。同时，它的对应目标位置的二进制展开式在第i层互为相反数，且其组合(je1[i],je2[i])只有一种情况(1,0)。因此，两者异或运算后得到的路由向量在第i层的组合(jd1[i],jd2[i])也有(1,0)、(1,1)、(0,0)和(0,1)这4种情况。

(jd1[i],jd2[i])的4种组合决定了路由向量在第i层以上的路由元素，相应对应着4种不同的修正可能性，其中(0,0)对应位置保持，(0,1)对应左侧位置保持，(1,0)对应右侧位置保持，(1,1)对应位置交换。至此，路由向量修正算法可以简化为：当jd1[i]＆jd2[i]=1时执行位置交换，否则执行位置保持。

进一步分析发现，当(jd1[i],jd2[i])为(1,0)、(0,0)、(0,1)这3种组合时，对应的起始位置组合(js1[i],js2[i])分别为 (0,0)、(1,0)、(1,1)。由于 js1和 js2相差小于等于2i，因此这3种组合对应的两个起始位置的二进制展开式在第i+1层到第n-1层的组合(js1[n-1:i+1],js2[n-1:i+1])只有 (0n-i-2,0n-i-2)和 (1n-i-2,1n-i-2)两种，即js1[n-1:i+1]=js2[n-1:i+1]。同时，由于(jd1[i],jd2[i])来源于第i+1层到第n-1层相同的路由区间，其对应的目标位置二进制展开式在第i+1层到第n-1层有：

由此可得：

这意味着当 (jd1[i],jd2[i])为(1,0)、(0,0)、(0,1)这3种组合时，其i+1层到n-1层的待修正路由向量是相等的，因此执行“位置交换”还是执行“位置保持”并不影响结果。此时，路由向量修正算法可以进一步简化为：无论(jd1[i],jd2[i])是什么值，都对第i+1层到n-1层的路由向量执行奇偶区间对应位置的交换修正，如图9所示。

由于本步骤的修正运算是固定的，对于硬件实现来说无需引入额外的运算模块，只需要将步骤2中计算结果的相应比特位利用拼接符“{}”指定固定的硬连线就可以实现。相对于Lee提出的递归算法，将POPCNT+LROTC运算转化为POPCNT+XOR运算，存在优化的可能性。

采用synopsys_design compiler-2018.06-SP1工具，结合UMC28nm工艺12track混合标准单元库(sc12mcpp140z_l28hpc_hpk_lvt_c30_ssg_cworst_max_0p81v_125c.db)，对两种算法实现的32 bit PDEP运算的置换参数产生模块进行综合对比。结果在时序约束为0.5 ns的情况下，获得了15%的面积优化，如表1所示。

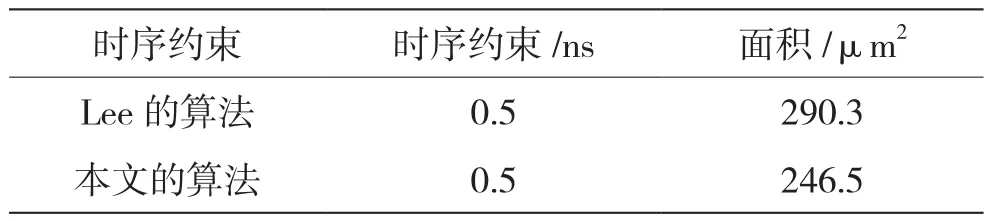
表1 32 bit PDEP运算置换参数产生模块对比

2.2 ROT运算

ROT运算是一种特殊的移位运算，根据移位方向d和移位位数m，选中输入数据的最低/最高n比特数据，然后将选中的这些数据移位到剩余数据的左侧/右侧，d∈{-1,1}，0≤m≤N-1。为了方便描述和推导，本文主要考虑RROT运算，如图10所示。

Lee等人发表的论文证明了RROT运算也可以采用Butterfly置换网络结构实现，同时提出了置换递归算法来对置换参数进行求解。

整个求解过程在硬件实现的时候被分解为两个步骤：

（1）对第 i行执行LROTC(0k(i),(m)mod2i+1)运算，其中k(i)=2i，0≤i≤log2N-1；

（2）将2n-i-1个LROTC(0m(i),(m)mod2i+1)拼接在一起得到第i层置换参数[1]。

作为对比，本文采用第一章提出的Butterfly网络的置换数学理论对RROT运算的置换参数求解过程进行推导。

为了方便描述，以下采用8 bit RROT运算进行分析。图11为一个8 bit的RROT置换运算。

根据Butterfly置换网络数学理论求解置换参数的标准流程如下。

（1）根据已知条件求解各目标位置上数据的起始位置。RROT运算的定义是根据移位位数m把输入数据最右侧m比特din[m-1:0]置换到输出数据中最左侧的m比特dout[N-1:m]的位置上，把输入数据最左侧N-m比特din[N-1:m]置换到输出数据中最右侧的m比特dout[N-m-1:0]的位置上。因此，有dout={din[m-1:0],din[N-1:m]}，输出数据各比特对应的起始位置为：

综上所述，目标位置je上数据的起始位置求解算法为(je+m)mod2n，如图12所示。

（2）初始排序和目标排序异或得到路由向量集合。根据（1）中的算法，可以得到N比特RROT运算输出数据的初始排序为：

只需将其与目标排序{N-1,N-2,…,2,1,0}做异或操作，就可以得到Butterfly网络的路由向量集合，如图13所示。

至此，N（N=2n）比特RROT运算置换参数的求解算法转化为N路并行“n比特加法+异或”运算。虽然逻辑深度由2n降为n，但是N个n比特加法器消耗的硬件资源不容忽视。值得注意的是，第j路n比特加法的其中一个输入是常数je，因此n比特加法逻辑可以进一步化简。

根据路由向量d(je)的求解算法[(je+m)⊕je]mod2n，由于mod2n属于硬件运算模块的附加属性，为了简化，在后续推导过程将其省略。

令A=je、B=m，则可将原算法转化为：

代入全加器的逻辑表达式：

得到：

代入进位产生函数和进位传递函数：

当je[i]=0时，有：

当je[i]=1时，有：

因此，得到递归函数：

（3）对路由向量集合进行修正得到置换参数。从步骤（1）化简后的RROT运算结果可以发现，第i层奇区间eb(i,2k+1)和偶区间ob(i,2k)中的对应路由点的起始位置js1和js2相差始终等于2i，因此两个起始位置的二进制展开式在第i层的组合(js1[i],js2[i])可能有两种情况(1,0)和(0,1)。同时，它的对应目标位置的二进制展开式在第i层互为相反数，且其组合(je1[i],je2[i])只有一种情况(1,0)。因此，两者异或运算后得到的路由向量在第i层的组合(jd1[i],jd2[i])只有(0,0)和(1,1)两种情况，如图14所示。

(jd1[i],jd2[i])的两种组合决定了路由向量在第i层以上的路由元素，相应的对应着两种不同的修正可能性，其中(0,0)对应位置保持，(1,1)对应位置交换。至此，路由向量修正算法可以简化为：当jd1[i]＆jd2[i]=1时执行位置交换，否则执行位置保持。

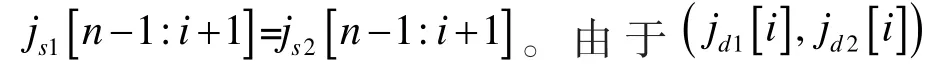
这意味着当(jd1[i],jd2[i])为(0,0)组合时，其i+1层到n-1层的待修正路由向量是相等的，因此执行“位置交换”还是执行“位置保持”并不影响结果。此时，路由向量修正算法可以进一步简化为：无论(jd1[i],jd2[i])是什么组合，都对第i+1层到n-1层的路由向量执行奇偶区间对应位置的交换修正，如图15所示。

最终得到：

由此可见，利用Butterfly网络的数学理论直接推导的结果与Lee提出的递归算法相同，因此两种算法实现的置换参数产生模块的优化程度一致，如图16所示。

3 结 语

本文通过数字表示的方法定义了Butterfly网络结构，通过数学方法深入研究网络结构的性质和特征，归纳总结出Butterfly网络的置换数学理论。此外，利用该数学理论重新分析了PDEP运算和RROT运算。对于32 bit PDEP运算，在时序约束同为0.5 ns的情况下，置换参数产生模块的硬件实现方案获得了15%的面积优化。对于RROT运算，获得了更加直观的置换参数推算过程。研究可为研究人员进一步分析开发Butterfly网络在其他比特置换运算中的应用提供了新思路。