基于0 特征值的复杂网络结构可控与优化研究

王 帅，李 婷

（陆军工程大学石家庄校区装备模拟训练中心，石家庄 050003）

0 引言

现实世界中，许多复杂的系统均可用网络系统来描述，如实际的互联网、电力网络、交通网络和抽象的人际社会关系网、生态链网络等。这些网络系统，由于其网络节点众多，网络拓扑结构复杂、链路多变，因此，常将这类网络称之为复杂网络系统。随着复杂网络系统研究的深入，复杂网络结构可控性成为众多学者研究的热点。2011 年，Liu［1］率先运用自动控制理论，在Lin［2］基础上研究了网络的结构控制问题，提出了复杂网络可控性理论，基于Kalman 秩判据开展复杂网络的结构可控性分析。文献［3］针对拥有自环节点的状态可调解网络研究了其可控性，并得出该网络可控仅需一个驱动节点的结论；文献［4］采用代数研究的方法，基于图的连通性开展控制节点选取研究，并对方法作了仿真验证；文献［5］研究网络控制过程的能量代价，证明了网络控制的复杂程度与网络结构紧密相关；文献［6］区分了网络控制节点作用，通过将网络节点划分为关键点、间歇点和冗余点，描述了网络控制的不同方式；文献［7］引入了节点控制能力概念，利用添加输入或者连边的方法，给出了网络精确可控的最小驱动点集合和极小被控点集合算法，但是算法仍然较为复杂且所得不是解析解；文献［8］针对有向图，引入“支配中心性”这一新的指标，评估有向图中顶点对其他节点的控制和观测能力；文献［9］基于PBH 可控性判定提出了严格可控性理论，实现了复杂网络即最小控制输入节点的数学求解。

战场指挥通信网络节点众多，属于典型的复杂网络系统，具有复杂和动态两种特征。要保证战场指挥通信网络的每个节点、每条链路都正常运行，需要消耗有限的管理控制资源，增大了网络的管理控制难度，使其安全性、稳定性、可靠性等方面问题凸显。目前的应对措施没有从战场指挥通信网络的动态结构这一根本原因出发，缺乏有效的解决方案，特别是未来战场指挥通信网络结构更加复杂，若无有效应对方案，将会制约战场信息网络建设。因此，需要研究战场指挥通信网络进行合理有效的结构控制方法，解决战场指挥通信网络结构可控性。

1 基于“0 特征值”的网络结构可控求解

开展复杂网络可控性研究，是基于结构控制理论将复杂网络视为一个系统，对于有n 个节点、m 个控制输入（m≤n）的网络系统，其运行状态方程可表述为［10-11］。

其中，A 为n 阶复杂网络邻接矩阵，x=（x1，x2，…，xn）T为n 维网络的运行状态变量，u=（u1，u2，…uM）T为m维输入变量，输入矩阵B 为控制输入矩阵。此时，在系统可控性判据约束下，系统的可控性由系统矩阵和输入矩阵决定，与系统外部具体输入无关。常用的网络结构可控性判定方法有两种：基本秩判据［1］和PBH 秩判据［10］。

1）基本秩判据是构造判定矩阵Q=［B AB A2B，… ，An-1B］=［I A A2，…，An-1］·B，通过矩阵Q 的秩来判定复杂网络系统是否结构可控，若rank（Q）=n，即判定矩阵满秩则网络是结构可控的，若rank（Q）＜n 则网络是结构不可控。

2）PBH 秩判据是构造判定矩阵Pk=［λkI-A|B］（λk为邻接矩阵A 所对应的所有特征值，k=1，2，…，n）。若所有k 对应的Pk都满足rank（Pk）=n，则复杂网络结构可控，如果有任一k 对应的Pk满足rank（Pk）＜n，则复杂结构不可控。

网络结构可控的秩判定说明了复杂网络的结构可控性判断，取决于复杂网络的邻接矩阵A 和控制输入矩阵B。网络结构可控最少控制输入点求解的思想是：基于邻接矩阵A 和输入矩阵B 构造判断矩阵，通过变换B 使判断矩阵满秩，B 变换对应的行及行数量即是复杂网络结构可控的最少输入控制节点数。

这里，将进一步对PHB 秩判据进行深入讨论。对于n 个节点的无向网络结构，则其邻接矩阵A 为n 阶对称矩阵，且元素仅为0 或1。因此，A 为较为特殊的一种矩阵，除了具备一般n 阶矩阵常见性质外，还有些特殊性质。

定理1：邻接矩阵A 为n 阶实对称矩阵，不考虑特征值的重复次数，则A 一定有n 个特征值。

证明：由矩阵理论［12-13］定理可知，对于n 阶实对称矩阵A 必能相似对角化，且相似对角化对角线上的元素即为A 的特征值，则A 有n 个特征值。

定理2：对于n 阶实对称邻接矩阵A，当矩阵秩rank（A）=k（k 为正整数且0＜k＜n），则λ=0 为A 的特征值，且为（n-k）重。

证明：A 为实对称矩阵，由于A 不满秩，则A必然存在值为0 的特征值。又由于A 必然能够相似对角化，则说明A 必然有n 个线性无关的特征向量，特征根重根对应线性无关的特征向量的个数等于其重数。由于A 的秩为k，则特征根λ=0 为重根，其对应（n-k）个线性无关特征向量，即λ=0 为（n-k）重。

推论1：对于n 阶实对称邻接矩阵A，不存在非0 特征之外的多重特征值。

证明：假设A 存在除0 以外的多重特征根λ'≠0，其重数为m（m 为正整数，0＜m＜n），则

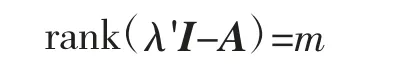
由于是对称矩阵，则rank（A）=n-rank（λ'I-A）=n-m。

而根据定理2，当rank（A）=n-m 时，特征值为0且其重数为n-（n-m）=m，这与λ'≠0 矛盾，因此，不成立。

推论2：对于n 阶实对称邻接矩阵A，当rank（A）=n 时，其有n 个特征值，这些特征值互不相同且均不为0。

证明：由于A 为实对称矩阵，当rank（A）=n 时，对于任意特征值λi都有

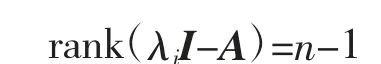
即所有特征值λi的重数都为1。下面证明任意λi≠0。

反证法。如果有一特征值为0，则满足

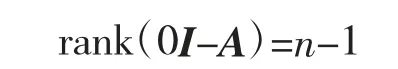
然而，rank（0I-A）=rank（A）=n，相互矛盾，故λ'≠0，证毕。

需要说明的是，当rank（A）=n，A 中行（列）向量均线性无关，此时网络可控结构是最少输入控制点数量为1。

综上所述，关于具有n 个节点的无向复杂网络结构可控，其最少输入控制点个数的求解转化为其邻接矩阵的“0 特征值”阶数。可得结论：对于具有n个节点的无向复杂网络，其最少控制输入点个数等于A 的0 特征值个数，即Nd为：

通常，将网络可控最少控制输入节点数与网络节点总数的比值定义为网络可控度nd，其表达式为：

网络可控度与Nd成正比，反映了网络结构可控的复杂程度，其值越大，说明网络最少输入控制节点数多，网络结构可控性差；反之，其值越小说明网络结构可控性较好。

2 基于“0”特征值的复杂网络结构优化策略

“0 特征值”对应的特征矩阵存在着零向量、重复向量和线性相关向量。这是向量包含若干节点（行），对这些节点通过调整边连接关系（增加或减少），最大限度消除零向量、重复向量和线性相关向量，则网络可控最小控制输入点就会减少，网络可控性就会提高。基于此，可以采用消除多重特征根的特征向量来优化复杂网络。在优化过程中，设定每个运行步长只允许对一条边进行一次增边或减边操作，具体优化策略如下：

2.2 镇咳平喘作用 天冬的镇咳、平喘、祛痰作用较强，最早在《本草纲目》中有记载，天冬酰胺是其镇咳的有效成分之一。天冬醇提物对浓氨水引起的小鼠咳嗽和由组胺引起的豚鼠咳嗽有显著抑制作用，其中对小鼠有较为明显的祛痰作用，对组胺引起的豚鼠哮喘模型起平喘作用[16]。天冬总皂苷可以抑制哮喘模型小鼠的气道炎性因子，显著降低白细胞介素(interleukin，IL)4、IL-13和COX-2的水平，抑制诱导型一氧化氮合酶的表达，还可增加巨噬细胞数量，减小支气管周围血管增生及胶原蛋白层厚度，抑制血管内皮生长因子表达[17]。

1）特征根向量集中是否存在零向量。如果存在，则逐个找到各零向量的对应行，对其进行增边操作。

2）特征根向量集中是否存在重复向量。如果存在，则逐个找到每个重复向量的对应行，随机选取其中节点进行增边或减边操作。重复上述步骤直至重复向量消除。

3）特征根向量集中是否存在线性相关向量。如果存在，则在线性相关向量的对应节点集中，任选一个节点进行连接改变，即进行边连接变换操作（一般为增边）。重复上述步骤直至线性相关向量最少。

在消除重复向量和线性相关向量过程中，减边操作可能会导致网络结构出现孤立节点（零向量），因此，在重复向量和线性相关向量优化后，均需进一步判断网络中是否存在零向量。当优化后的特征矩阵不存在零向量和重复向量，线性相关向量将至最少时（不一定为0），优化完成。此时，特征矩阵（-A）的行相关性最小，网络结构可控性得到提高。基于“0 特征值”的网络结构优化流程如图1 所示。

图1 网络结构优化流程

3 实际网络应用分析

以某指挥通信网为例研究，该指挥网包括1 个中心指挥子网、1 个后方保障子网、1 个机动指挥子网，7 个运行子网，每个子网包含若干通信节点；同时阵地间5 个通信节点的干线通信网，另有卫星中继通信节点、3 个卫星地面站节点和2 个卫星背负站接入节点，共51 个通信节点，涉及的通信方式有电台、微波、光纤、卫星等。该指挥网结构为层级结构，其中，干线通信子网和微波中继子网采用的网状拓扑，构成点对点的网状连接；卫星中继通信子网采用星型拓扑结构，由地面站和背负式接入站构成中继通信链路；其余通信子网采用星型拓扑结构，各个子网以中心节点核心，各个子网核心节点通过干线通信子网及中继子网能够连接。由于战场指挥通信网络为双向传递，而有向网络通常用于描述单向信息传递，且由于研究指挥通信网络的结构可控性，仅考虑网络中节点的连接情况而不考虑节点间的距离和介质，即不考虑网络中边的权值，因此，可将战场指挥通信网络限定为无向、无权网络。此外，指挥通信网节点的实际应用决定了网络为无自环网络。同时研究过程中，为了保证节点控制输入的有效性，将每一个控制输入视为单控制输入，即每个控制仅能对某一节点进行输入。此时，将51 个通信节点分别进行编号，根据网络节点的连接关系，绘制出其拓扑结构图，共包括69 条边，如图2 所示。

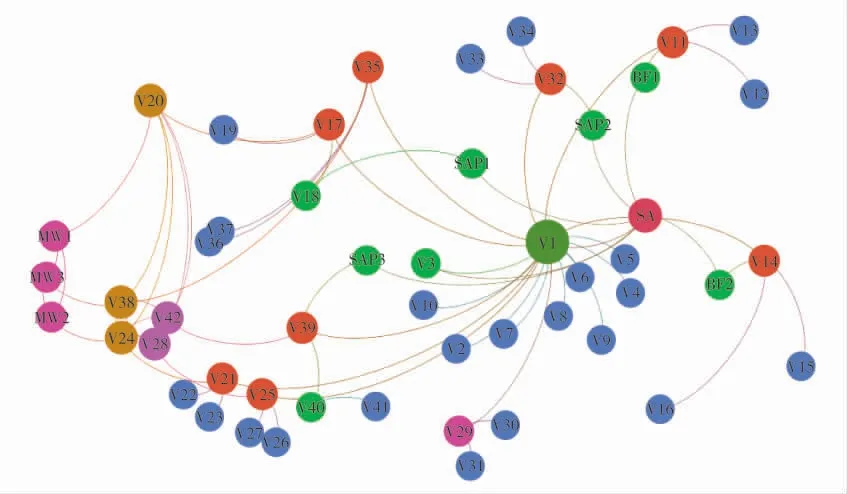
图2 某指挥通信网络结构图

由网络的拓扑结构，得出该网络对应的邻接矩阵A 为51×51 对称仿真，其简略表示如下：阵A，对其求秩，得

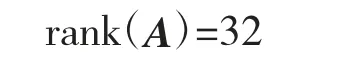
其次，根据“0 特征值”特性可知，邻接矩阵A 存在重数为19 的“0”特征值，则可得该网络结构可控的最少控制输入点个数Nd为

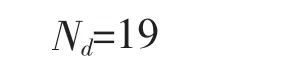
再次，求解0 特征值对应的特征矩阵（-A）进行初等变换，求解出其存在8 组重复向量和5 组线性相关向量，具体如表1 所示。

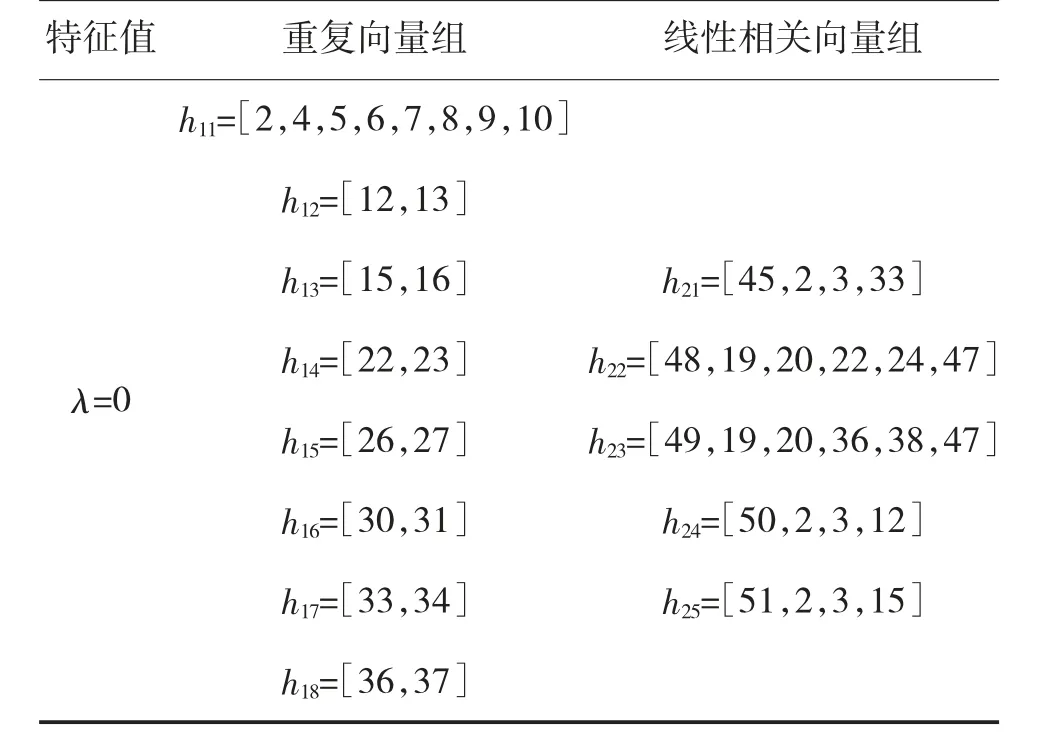
表1 “0 特征值”对应特征矩阵初等变换结果数据

网络可控最少输入节点是要从这8 组重复向量和5 组线性相关向量组包含的节点中选取19 个节点为控制最少输入点。从计算结果可知，重复向量组和线性相关向量组之间有交叉节点，分别为2、12、15、22、33、36；线性相关向量组之间也有交叉点，分别为：19、20、47 共9 个节点，具体实施时，这些节点可以视为必选点，剩余10 个节点可以从剩余节点中按照PHB 置换原则进行选择，这样可以进一步缩小最少输入控制点集合。

依据“0 特征值”对应特征向量的优化策略，对该网络进行优化，经过32 步优化操作，得到优化后的网络结构，如图3 所示。

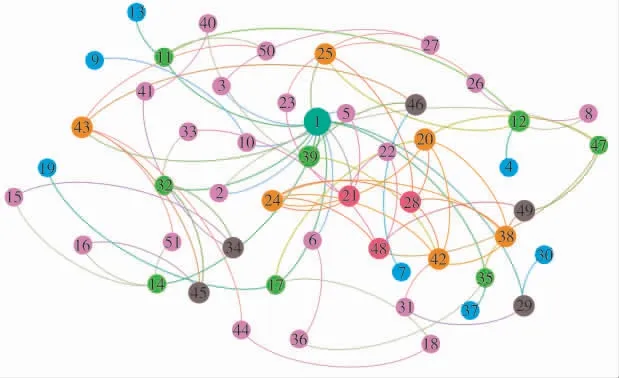
图3 结构优化后的旅级战场信息网络结构图

对优化前后网络结构特征参数进行统计，得到优化前后网络结构部分指标数据对比如表2 所示。

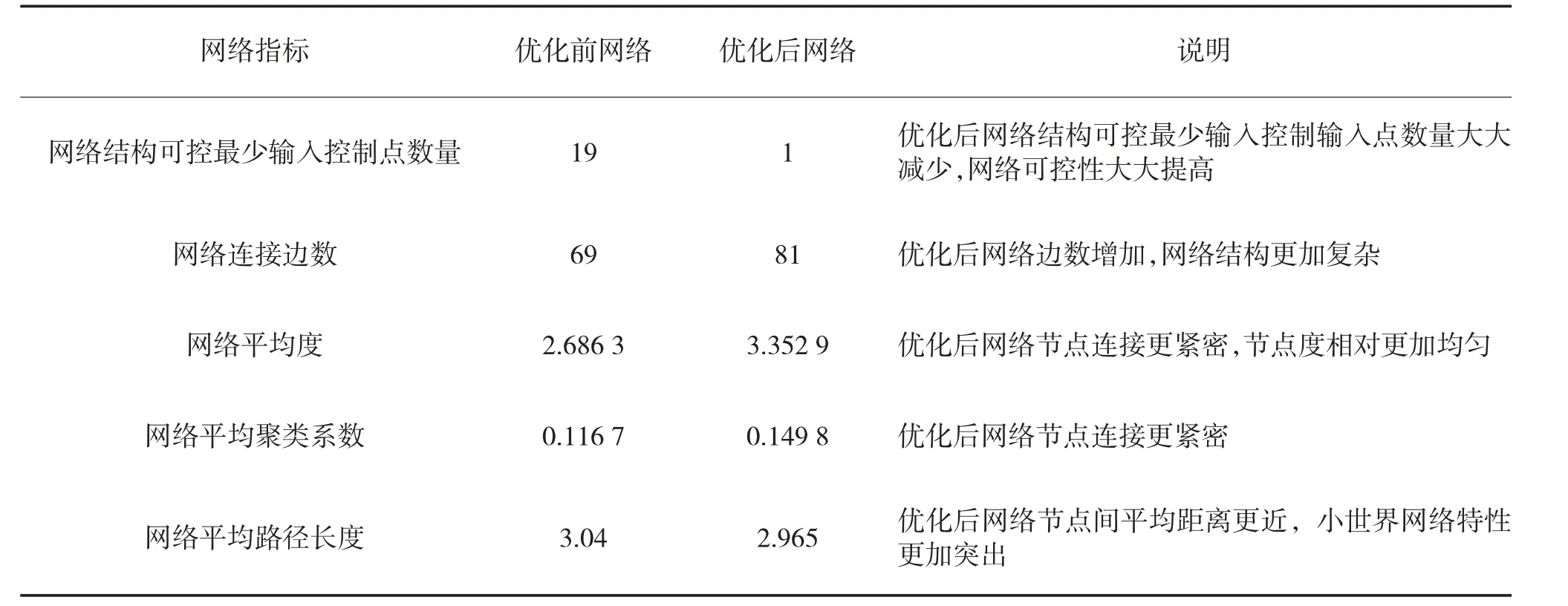
表2 网络优化前后网结构特性对比表

从表1 可以看出优化后的网络增加了部分边数，结构更加复杂，但是网络结构指标数据相比先前网络结构有了明显优化，可控性大大提到。当然这个优化过程可以进一步结合网络节点的使命任务和通信方式，则优化后的网络更具价值。

进一步地，从网络结构抗毁性对优化前后网络性能进行对比。分别采用随机攻击和蓄意攻击［14-15］两种方式进行。随机攻击时考察网络的连通状态随机攻击网络节点数量增加的变化情况，为消除随机性，建立200 次攻击样本进行统计。则网络优化前后网络达到不连通状态所需要的攻击节点数量，如图4 所示。

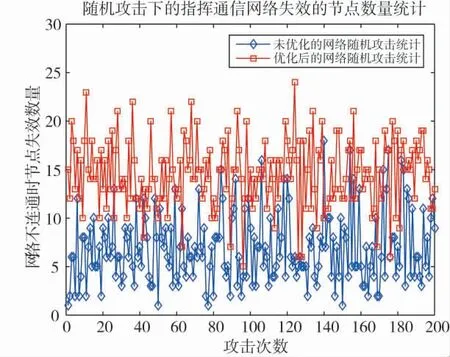
图4 随机攻击条件下网络失效随攻击节点数量变化图

由图4 可见，随机攻击条件下，优化前网络平均遭受6 个节点的攻击网络便处于不连通状态，优化后网络平均遭受14 个节点的攻击网络，才能失效为不连通，网络抗随机攻击性能大幅提高，证明了在随机攻击条件下网络结构优化策略的有效性。

蓄意攻击分别采用按节点度和节点介数进行攻击，考察网络最大连通子图数量变化和网络效率［16］变化情况，如图5 所示。

图5 不同攻击条件下网络性能变化随攻击节点数量变化图

由图5 可见，随意攻击条件下，优化前网络的最大连通子网节点数量和网络效率下降相对较慢；按节点度攻击条件下，优化前网络的最大连通子网节点数量和网络效率均剧烈下降，网络很快失效；按节点介数攻击条件下，优化前网络的最大连通子网节点数量和网络效率呈现快速下降。然而，同样攻击条件下，最大连通子图节点数量和网络效率较优化前下降过程更为缓慢，表现了更好的抗毁性能，也证明了蓄意攻击条件下网络结构优化策略的有效性。

4 结论

基于“0 特征值”的网络结构可控最少输入点数量求解和结构优化策略，本质上是将复杂网络结构可控分析转化为网络邻接矩阵特性研究上，由邻接矩阵便能迅速确定网络结构可控最少输入点数量以及控制节点范围，对邻接矩阵初等行列变换能够有效优化网络结构。这一结果在对比网络结构特性统计数据和抗毁性测试方面得到印证，可将其用于战场指挥通信网络的规划设计、结构分析等，对于维护指挥通信网络的安全性、稳定性、可靠性等具有很强的现实意义。但是，该方法目前仅适用于无向无权无自环网络，关于有向、有权和有自环网络的结构可控与优化，还需要进一步研究。