基于GeoHash 索引的A*算法优化*
2021-08-06张海亮
张海亮,张 征
(1.山西工程科技职业大学,山西 晋中 030619;2.浙江工业大学机械工程学院,杭州 310014)
0 引言
随着计算机技术、网络技术的成熟,包括无人驾驶在内的道路规划[1]与最短路径算法[2]逐渐成为研究热点。
A*算法[3-4]作为最短路径中最成熟的算法之一,在广度优先搜索的基础上,以启发式搜索为基础,同时具有Dijkstra 算法[5]在搜索速度和效率上的优势。A*算法在启发式搜索的过程中,采用了曼哈顿权值函数作为最优邻接点的评估标准,相对于广度优先搜索,减少了大量的无效邻接点的扩展验证,有效提高了算法的搜索效率[6-8]。但是对于大数据量下的网络拓扑,A*算法在进行空间搜索时,算法效率呈阶梯式下降,且起始点和目标点越远,中间的间隔越大,A*算法在进行最优邻接点选取时的时间就越长。GeoHash 索引[9]以地理经纬度信息为基础,将经纬度信息转化为GeoHash 值赋值给栅格节点,可以在A*算法中作为最优邻接点的权值评估参考,进一步确定最优邻接点。
1 A*算法
A*算法在求解最短路径时(如图1a 所示),整体的思路是从起始点A 开始,通过迭代方式查找相邻方格,不断扩展直至找到目标点B。在迭代查找相邻方格时,采用曼哈顿函数对相邻方格进行评估,通过对比每个相邻方格与目标终点之间的方格数,来判断哪个方格为最优邻接方格,并将其作为下一步选择的起点,然后再进行迭代查找,在迭代的过程中,每次都对当前起点的邻接方格进行曼哈顿函数评估,每次都计算出一个最优邻接点作为下一步的起点,这样不断向外扩展,一直扩展到目标终点为止。因为在迭代的过程中,是以当前点的邻接点与目标终点的网格数作为评估标准,所以A*算法最终一定会查找到目标终点。
A*算法把Dijkstra 算法(靠近初始点的结点)和BFS 算法(靠近目标点的结点)的信息块结合起来。在讨论A*的标准术语中,G(n)表示从初始结点到任意结点n 的代价,H(n)表示从结点n 到目标点的启发式评估代价(heuristic estimated cost)。在图1b中,yellow(h)表示远离目标的结点,teal(g)表示远离初始点的结点。当从初始点向目标点移动时,A*权衡这两者。每次进行主循环时,它检查f(n)最小的结点n,其中,F(n)= G(n)+ H(n)。
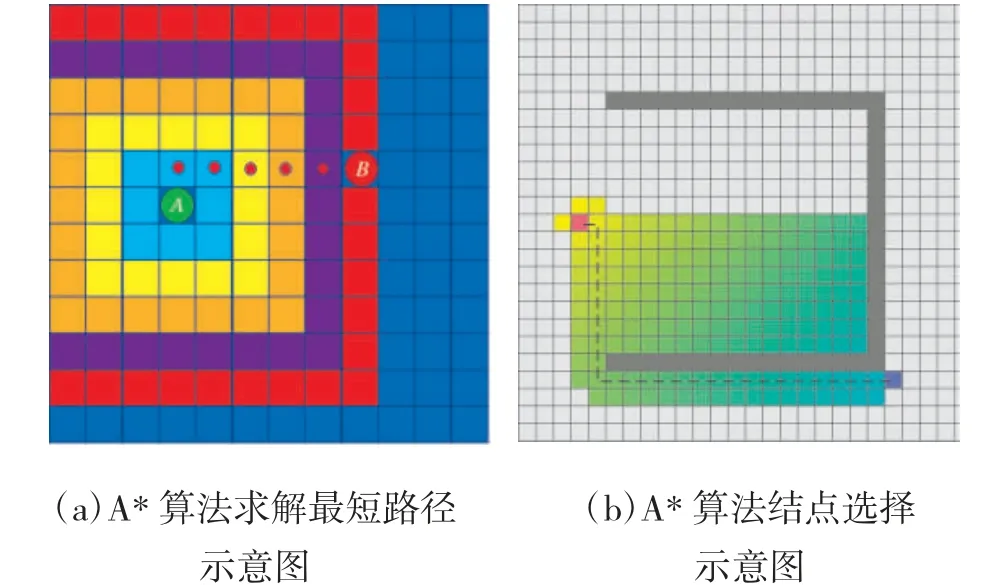
图1 A*算法示意图
通过曼哈顿函数进行评估选择最优邻接点也称为启发式搜索。A*算法在进行当前点的最优邻接点选取时,使用曼哈顿函数评估,而曼哈顿函数计算的是起始点和目标点之间的网格数,然后乘以固定系数,作为每个邻接点的对比值。图2 显示了两个不同位置的曼哈顿函数所对应的区别,图2(a)中,当邻接点在起点A 上方时,邻接点与目标点B之间的曼哈顿距离评估值为4 M(M 为单个网格距离);图2(b)中,当邻接点为右下侧时,邻接点与目标点B 之间的曼哈顿距离评估值为5 M(M 为单个网格距离)。所以应该选择上方的邻接方格作为最优邻接点。在寻找A 点的邻接点时,上侧的邻接点到目标终点B 的曼哈顿权值小于右下角邻接点到目标终点B 的曼哈顿权值,故可对A 方格的8 个邻接方格中的曼哈顿权值进行比较,选取权值较小的邻接点作为前进的方向,曼哈顿权值较大的邻接方格则直接忽略不进行下一步的扩展。

图2 不同位置曼哈顿函数评估图
当起点和目标点离的较远时,每个作为起点的方格都要进行8 次邻接点与目标终点之间的网格计算,且每次计算时起点都不同,当数据量较大时,就需要较多的时间来完成计算,从地理信息角度来看,A*算法仍有较大的优化空间。
2 GeoHash 函数评估
地理信息系统(GIS)[10]中,对地理位置信息有一种快速查找索引方式——GeoHash,GeoHash 是将对象所在的经纬度位置转化为Base32 字符串值,并将GeoHash 值赋给对象所在的网格。由于GeoHash值是按照一定的规律来进行计算的,所以在使用A*算法求解最短路径时,可通过对比网格的GeoHash值来替代曼哈顿权值的计算[11],省去邻接网格与目标网格进行曼哈顿函数计算的过程,从而在大数据量的情况下,能够优化计算时间,大大提高A*算法的计算速度。
2.1 GeoHash 算法
在GIS 中,某一对象所在的位置,均使用经纬度来进行标记,处理网格时,通过采用GeoHash 索引值对一个对象所在的具体位置进行描述。例如,需要对经纬度数据为(121.420 168,31.200 381)进行GeoHash 值描述时,可以通过数值转换获得GeoHash 值,这个GeoHash 值代表的不是一个点的位置,而是一块区域位置,经纬度数值精度越高,则区域范围越小;反之,精度越低,所代表的区域范围越大。
由于经纬度的精度不同,GeoHash 算法得到的值长度也不相同,为了和最短路径相结合,使得计算出来的路径线路符合实际的道路方向,采用与地图街道级别相同视野的精度作为讨论的标准,故采用经纬度精度为小数点后6 位小数的道路图作为讨论对象。在最短路径算法的实现过程中,均以经纬度精度为6 位小数作为GeoHash 的算法精度进行处理,对于经纬度为(121.420 168,31.200 381)计算GeoHash 值时,则得到wtw36zz 这样的GeoHash 值。
在精度为6 的情况下,经纬度转换为GeoHash值可分为4 步:
第1 步:对经纬度范围以(-90,90)和(-180,180)进行对半取值,以经度为例,value=113.918 646,大于中间值为1,小于中间值为0。这个区间如何得来的呢?要知道经度的范围是[180,-180],那么中间值就是0,判断是在[180,0]还是[0,-180],如果在[180,0],就是1,然后缩小区间。查看当前经纬度所在区间,前半区间为负区间,值为0,后半区间为正区间,值为1,递归计算。记录经纬度所在区间值,经度获取的二进制数值为110101100101011111,纬度获取的二进制数值为10101100010111111。
第2 步:将经纬度对半划分区间得到的二进制数进行组合,以奇数为纬度,偶数为经度进行组合,得到一长串二进制字符串。图3 计算出的二进制字符串为:111001100111100000110011011111 11111。
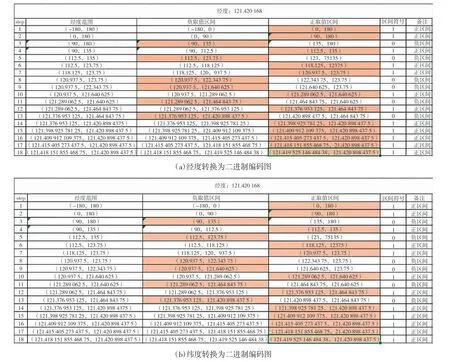
图3 经纬度二进制编码转换图
第3 步:将获取到的二进制字符串以每5 个数为一组,将每一组转换成十进制数字。
第4 步:将取得的十进制数字参照Base32 编码转为对应的字符,将得到的字符连起来即为wtw36zz。
按照Base32 的字符集取值,最终的GeoHash 的结果为wtw36zz。

图4 十进制数字与Base32 编码对应关系图

图5 二进制编码转换为Base32 编码
2.2 GeoHash 对比原理
每个方格的GeoHash 值是根据方格所在位置的经纬度进行计算的,随着经纬度的变化,方格的GeoHash 值也呈规律性变化,由于GeoHash 值使用Base32 值的字符串来表示,所以方格之间的距离远近可以通过方格的GeoHash 值来进行判断。图6 为上海的一块区域,可以通过对比方格的GeoHash 值来查看方格之间的距离关系。
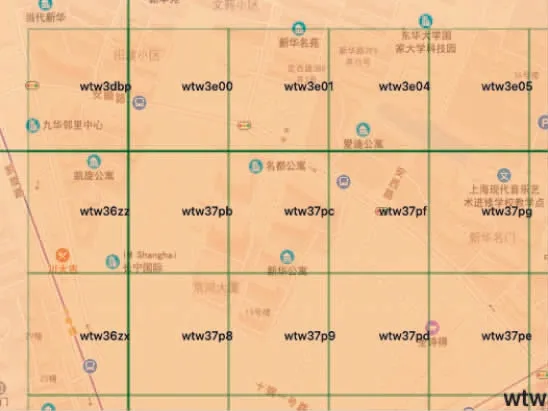
图6 GeoHash 索引
为方便查看,首先取第2 行来进行对比,(2,1)方格区域的GeoHash 值为wtw36zz,当经度增加时,(2,2)方格区域的GeoHash 值为wtw37pb,(2,3)方格区域的GeoHash 值为wtw37pc,(2,4)方格区域的GeoHash 值为wtw37pf,(2,5)方格区域的GeoHash值为wtw37pg。第2 行左侧依次到右侧,第1 个方格与第2 个方格比较,去除前面相同的wtw3 部分,经度越大,则其不同部分的第1 位数值越大,也就是7>6;第2 个方格与第3 个方格比较,去除前面相同的wtw37p 部分,后面的c>b,第4 个方格的f>c,第5个方格的g>f;然后选取整个区域第3 列来比较纬度变化情况,(3,3) 方格区域的GeoHash 值为wtw37p9,当纬度增加时,(2,3)方格区域对应的GeoHash 值为wtw37pc,c>9,(1,3)方格区域所对应的GeoHash 对应的值为wtw3e01,去除前面相同的wtw3,第4 位的e>7。遍历图中所有方格,GeoHash值都遵循一个相同的变化规律,那就是:随着经纬度的增加,其对应的方格所在的GeoHash 值,是随着Base32 的字符顺序逐级增加的,而且当个位数不够增加时,则在更高一位进行递增。图6 中,从经纬度最小的左下角wtw36zx(121.420 034,31.199 44)逐位递增到右上角wtw3e05(121.425 318,31.201 909),由此可以得出,在经纬度的精度确定的情况下,经纬度所对应的方格的GeoHash 值的规律是随着经纬度的增加,其GeoHash 值越大。因此,在进行A*算法时,可以通过GeoHash 值对比来确定最优邻接点。
2.3 GeoHash 作为评估函数的A*算法
从下页图7 可以看到,(a)中起点A 的GeoHash值为wtw37pb,目标点B 的GeoHash 值为wtw3e05,当选择起点A 的上方邻接点时,其GeoHash 值为wtw3e00,与目标点相同的部分有wtw3e0,共有6 位相同数;而(b)中选择下方的邻接点时,其GeoHash值为wtw37p8,与目标点B 的GeoHash 值wtw3e05只有4 位相同数,而且wtw3e00 与wtw37p8 相比较,第5 位的e 从Base32 上的编码上更接近于B 点GeoHash 值wtw3e05,所以(a)中上方的邻接点更接近于目标点B,由此可判断上方邻接点相对于下方邻接点为最优邻接点。右侧的邻接点(wtw37pc),与上方的邻接点在最短路径的距离上是相同的,求解最短路径的目的是找到最短路径,故上述任一点均可选择。
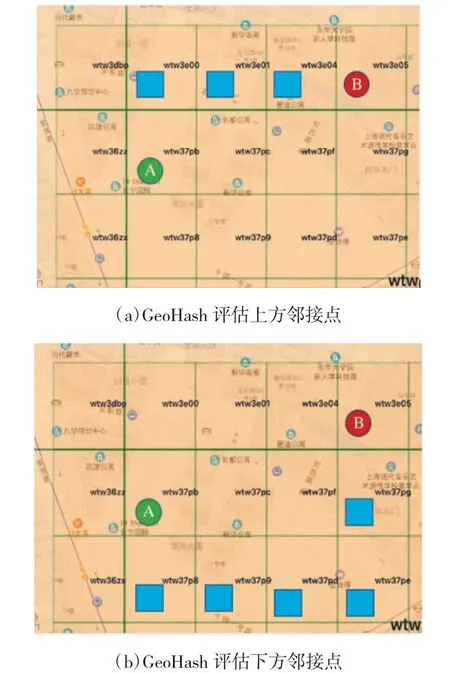
图7 不同位置曼哈顿函数评估图
由于经纬度是固定存在的位置信息,且不会发生改变,所以在查找最短路径时,可根据起始点的位置和目标点的位置,确定这两点的GeoHash 值,比较其GeoHash 值相同的部分以及不同的部分,确定其大小关系,进行查找最优邻接点时,对比邻接点的GeoHash 值与目标点的GeoHash 值,越接近(Base32 编码为顺序)目标点的GeoHash 的方格,则作为最优邻接点的候选点。GeoHash 是固定字符值,可直接进行字符比较,无需像曼哈顿评估函数那样计算当前邻接点和目标节点之间的方格数,可大大提升计算效率。
以下为使用GeoHash 值作为最优邻接点评估函数的A*算法过程,如图8 所示。
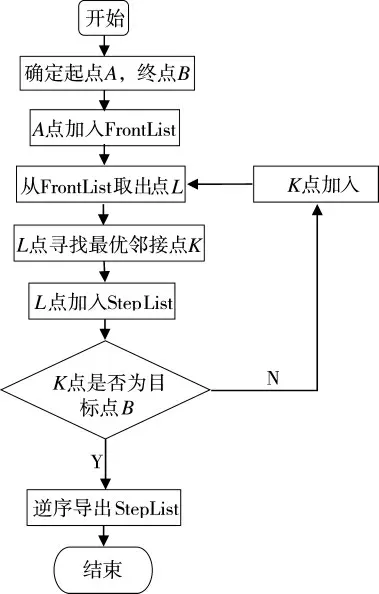
图8 GeoHash 值作为最优邻接点评估函数的A*算法过程
1)首先将A 点作为待处理节点存入FrontList集合中,FrontList 包含所有需要进行扩展但是还没有进行扩展的节点集合。
2)以FrontList 作为链表,将里面的每个节点作为新的起点L,寻找起点所有可到达的邻接方格,并将查询到的最优邻接点存在FrontList 中,最优邻接点根据邻接方格的GeoHash 值与目标点的GeoHash值对比进行判断,与目标点的GeoHash 值相同部分最多的方格即为最优邻接点方格。将L 点从FrontList 中删除,并将L 点存入到StepList 列表中。
3)循环执行步骤2。当然,有一种特殊情况需要处理,就是当使用L点作为起点查找邻接点K,再以邻接点K 查找邻接点时,L 点也会作为K 点的邻接点被查找到,这种情况下,需要把L 点排除,也就是说已经保存在StepList 或者FrontList 的点不能再次作为邻接点进入FrontList,否则会形成一个死循环。
4)当查找到的邻接点为目标点B 时,跳出循环,逆向查找起始点序列,得到最短路径。
从GeoHash 的编码规则来看,GeoHash 算法和曼哈顿函数的原理是一样的,曼哈顿函数以当前点与目标点之间的方形区域网格数作为评估标准,网格数越少的邻接方格作为最优邻接点;而GeoHash算法以当前点GeoHash 编码值与目标点GeoHash值作为评估标准,相同位数越多的邻接方格作为最优节点。在具有GeoHash 值的网格进行最短路径分析过程中,两个网格GeoHash 值字符相同的位数越多,则两者之间的方形区域网格数越少,也就代表两者距离越近。GeoHash 是以索引值的形式对坐标位置定义,是已经存在的数据,其优势在于节省了以曼哈顿距离函数作为评估标准时,对每次的最优邻接点求解时,依次计算邻接点与目标点之间的网格计算过程。
因为GeoHash 算法是针对于地理信息系统中经纬度的索引算法,使用GeoHash 算法对A*最短路径算法进行邻接点评估,适合存在实际地理位置也就是有经纬度的情况下,对于只存在网络节点和权值的拓扑网络,没有实际的评估意义,当然也可以将拓扑网络根据其权重进行地理位置模拟以及GeoHash 值计算,从实际工作复杂度和工作效率上来说意义不大。
[1]苏浩,李钦富,蔡俊.A*算法在基于道路网的路径规划中的应用[J]. 中国电子科学研究院学报,2010,5(4):419-422.
[2]胡恩祥,汪春雨,潘美芹.基于密度峰值剪枝后的最短路径聚类算法[J].应用科学学报,2020,38(5):792-802.
[3]肖自兵,屈耀红,袁冬莉.基于障碍信息的高效A-Star 航路规划算法[J].火力与指挥控制,2018,43(9):71-75.
[4]卫珊,王凌,王斌锐,等.A*算法的改进及其在AGV 路径规划中的应用[J].自动化仪表,2017,38(11):51-54.
[5]贺丽娜,楼佩煌,钱晓明,等.基于时间窗的自动导引车无碰撞路径规划[J].计算机集成制造系统,2010,16(12):2630-2634.
[6]罗子涵,彭旷,戴铭酉,等.基于改进分层A*算法的雨天车辆导航方法[J].计算机应用,2020,40(s2):210-214.
[7]岳秀,张超峰,张伟,等.基于A-Star 和改进模拟退火算法的航迹规划[J].控制工程,2020,27(8):1365-1371.
[8]王中玉,曾国辉,黄勃.基于改进双向A*的移动机器人路径 规 划 算 法[J]. 传 感 器 与 微 系 统,2020,39(11):141-143,147.
[9]YU K,QU C Y.Prediction and optimization of sharing bikes queuing model in grid of Geohash coding[J].Measurement&Control,2020,53(7-8):1250-1266.
[10]SHAO Z F,HUQ M E,CAI B W,et al.Integrated remote sensing and GIS approach using Fuzzy-AHP to delineate and identify groundwater potential zones in semi-arid ShanxI Province,China [J].Environmental Modelling &Software,2020:134.
[11]WANG C B,WANG L,QIN J,et al.Path planning of automated guided vehicles based on improved A-Star algorithm [C]//2015 IEEE International Conference on Information and Automation:2015 IEEE International Conference on Information and Automation(ICIA),in conjunction with 2015 IEEE International Conference on Automation and Logistics,Lijiang,Yunnan,China,2015.
