暖机对航空发动机性能模型的影响分析
2021-08-06钱仁军宋汉强李本威朱飞翔
钱仁军,宋汉强,李本威,朱飞翔,张 赟
(1.海军航空大学,山东 烟台 264001; 2.海军研究院,上海 200436)
1 引言
涡扇发动机在启动成功后,按照规定需先进行暖机操作,即将高压转子转速保持在一定转速,并维持一段时间,再将发动机由慢车运行到最大状态。对应飞机的起飞流程,即在起飞前,需先将飞机运行到暖机位进行暖机,然后行驶到起飞位准备起飞。暖机的存在影响了飞机出动程序和出动路线的规划,严重制约了飞机的出动效率,已经成为提高飞机出动效率的瓶颈问题。
已有研究表明,发动机不暖机直接运行到最大状态,相比暖机后叶尖间隙有所增大[1]。而发动机性能与叶尖间隙密切相关,叶尖间隙的变化会直接影响到部件的效率和流量,并进一步影响整机性能和油耗[2]。台架数据也表明,发动机不暖机直接运行到最大状态与暖机后的最大状态在性能上存在差异。
航空发动机具有制造成本高和试验费用高的特点[3],直接在发动机本体上进行暖机对整机性能的影响试验,不仅试验费用非常昂贵,同时由于暖机对发动机结构的影响还可能导致对发动机造成额外损伤。发动机性能模型仿真技术已经成为避免以上问题的有效手段[4]。利用发动机性能模型替代真实发动机进行仿真研究,可以获得不同环境参数和不同状态下发动机的总体性能,以及一些台架试车无法测量的参数。
发动机模型建模方法主要有解析法和试验测定法[5]。解析法又称为部件法,是利用部件特性数据通过气动热力学和共同工作方程建立的模型[6]。试验测定法是利用不同条件下发动机测得的试验数据,通过系统辨识方法建立模型,因此试验测定法建立的模型又称为辨识模型[7-8]。相比部件级模型,辨识模型对试验数据要求更高,其试验成本和试验难度也都高于部件级模型。
考虑到不暖机直接将发动机运行到最大状态可能对发动机造成的损伤,无法对发动机进行长时间或者不同环境下的多次不暖机试车,无法获得足够的不暖机试验数据,因此,无法通过建立辨识模型对发动机输入条件进行泛化。故本文采用部件法建立发动机的性能模型。
发动机部件级建模方法最早是由NASA Lewis研究中心提出[9-10],并在90年代结合面向对象的设计思想,进一步推出了推进系统数值仿真计划(NPSS)[11]。国内在20世纪90年代后陆续开始采用变比热法进行部件级建模,其建模方法至今在新型发动机建模领域仍有广泛应用。盛柏林等[14]沿着某型涡桨发动机的气路结构进行了部件级建模,并对比了发动机设计点数据和模型性能参数计算结果,验证了模型的有效性。王元等[15]对变循环发动机建模方法进行了研究,在涡扇发动机性能模型基础上重新构建了风扇和外涵道模型,并利用NASA试验数据验证了模型有效性。王逸维[16]建立了一种三轴拉力式对转桨扇发动机的仿真模型,其核心机建模采用的是三轴涡轴部件级模型,并基于该模型对桨扇发动机进行了性能评估。以上不同类型发动机性能模型的核心均为利用气动热力学描述发动机工作的物理过程,并结合发动机共同工作方程,完成发动机性能模型的构建。
本研究采用变比热法对某型涡扇发动机进行了部件级建模,并利用台架测试数据验证了模型的有效性。将发动机暖机与不暖机2种情况下的实测数据与模型计算值进行对比,分析了暖机对发动机性能模型的影响。
2 发动机部件模型
部件的计算模型是指已知输入参数,通过气体动力学和工程热力学计算出部件的输出参数。沿着涡扇发动机的气体流路,对风扇、压气机、燃烧室、高压涡轮、低压涡轮、混合室、加力燃烧室和尾喷管等部件进行建模,并在尾喷管得到发动机性能的输出参数。将发动机各部件的计算模型与发动机共同工作方程相结合,就得到发动机的性能模型。本文所用涡扇发动机部件截面如图1所示。

图1 涡扇发动机截面示意图
2.1 风扇模型
定义风扇特性数据中等转速线上增压比πc0对应的压力比函数[17]为:
(1)
式中:πmin为该转速线上最小增压比;πmax为该转速线上最大增压比。
1) 增压比πcL、效率ηcL和空气流量Wa2cor的插值计算
(2)

(3)
(4)

(5)
由插值结果的换算流量Wa2cor,求得Wa22:
(6)
(7)

(8)
压气机的部件模型具体计算过程与风扇的计算过程相似,不同的是需要增加压气机的引放气。
2.2 燃烧室模型
(9)
式中,σb为燃烧室总压恢复系数。
2) 油气比fb和燃烧效率ηb的计算
根据能量平衡和质量平衡公式:
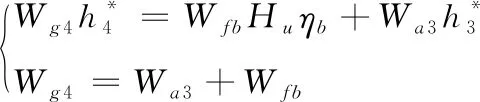
(10)
得到油气比fb计算公式:
(11)
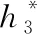
3) 燃油流量Wf的计算
Wf=Wa3fb
(12)
2.3 高压涡轮模型


(13)

(14)
(15)
根据换算流量求解出实际流量Wg45,进而求得高压涡轮功率LTH:
(16)
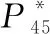

ψ45,ideal=ψ4+Rgln(1/πTH)
(17)
计算求出落压比πTH:
πTH=[exp((ψ45,ideal-ψ4)/Rg)]-1
(18)
(19)
低压涡轮具体计算过程与高压涡轮的计算过程相似,不同的是需要改变冷却空气量。
2.4 外涵道模型
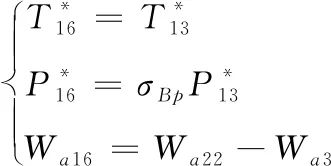
(20)
式中σBp为外涵道总压恢复系数。
2.5 混合室模型
1) 出口油气比f6和出口流量Wg6的计算
根据出口燃油流量Wf6=Wg5f5/(1+f5),出口空气流量Wa6=Wg5/(1+f5)+Wa16,可以求出油气比f6:
f6=Wf6/Wa6
(21)
出口燃气流量Wg6:
Wg6=Wg5+Wa16
(22)
(23)
(24)
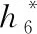
3) 内、外涵入口静压P5和P16的计算
根据流量公式和流量函数,可求得入口绝热指数k5和速度系数λ5。将速度系数λ5和绝热指数k5代入压比函数公式:
π(λ)=(1-(k-1)/(k+1)·λ2)k/(k-1)
(25)
求出内涵入口静压P5:
(26)
外涵冷流入口的速度系数λ16和静压P16计算过程与内涵相同。
流量连续方程:
(27)
动量守恒方程:
(28)
2.6 加力燃烧室模型

开加力时,计算过程与主燃烧室相同;不开加力时,计算过程为:
(29)
式中,σab为加力燃烧室总压恢复系数。
2.7 尾喷管模型
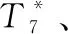
喷管模型为收敛—扩散喷管,其流动过程为绝能过程,相关气流参数:
(30)
2.7.1设计点状态

(31)
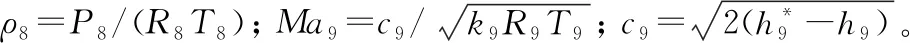
2.7.2非设计点状态

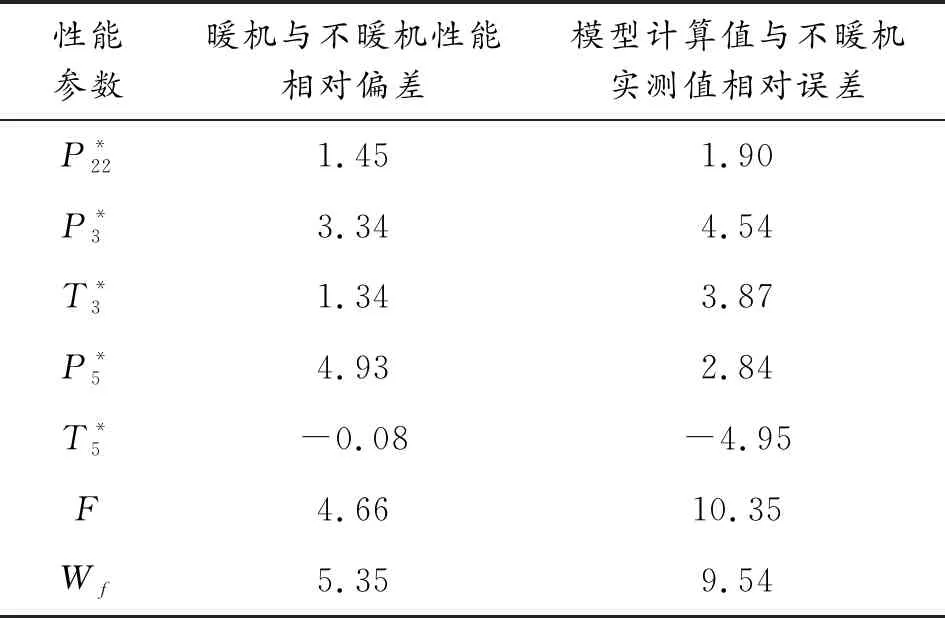
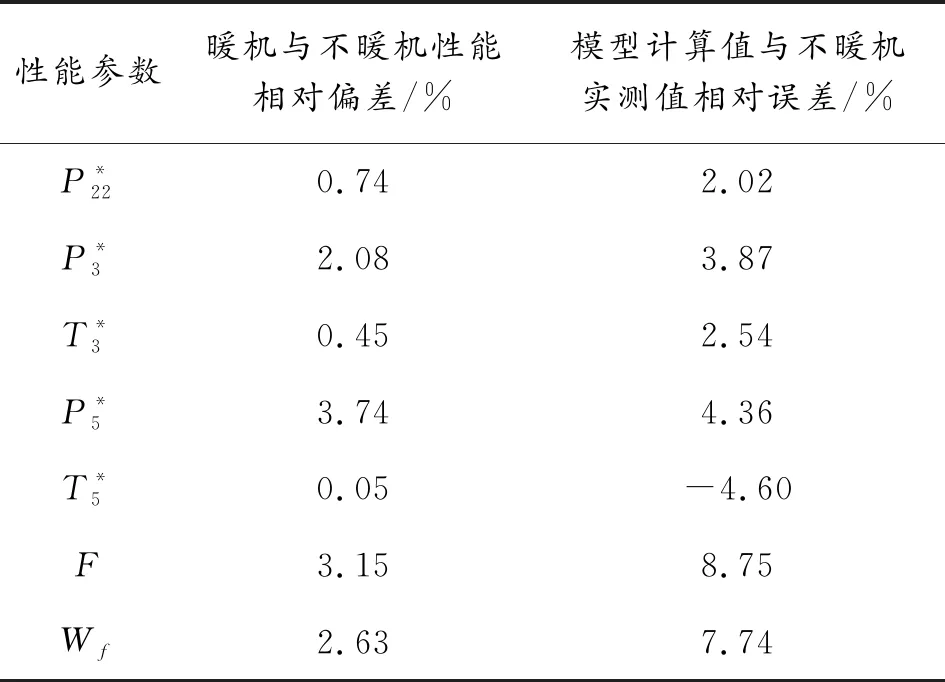
1)P8 重新计算出口静温T9,继而得到出口气流速度c9: c9=Wg9/[P9/(R9T9)A9] (32) (33) 2)P8≥PH ① 理想完全膨胀 此时A9=A9,ideal,P9=PH。计算过程同设计点相同。 ② 不完全膨胀 ③ 过度膨胀 此时A9>A9,ideal,且在出口将会形成激波。重新迭代计算T9和h9,并计算激波前后的压力为: (34) 当P9y>PH时,不考虑斜激波的损失,可以近似认为激波前气流参数就是喷管出口参数。当P9y 2.7.3发动机性能参数计算 发动机推力: F=Wgc9-WaV+(p9-pH)A9 (35) 单位推力: FS=F/Wa (36) 耗油率: (37) 根据发动机共同工作关系,发动机在稳态工作过程应满足的流量、功率和静压平衡方程为: 高压涡轮流量平衡: (Wa3+Wfb-Wg4)/Wg4=0 (38) 高压涡轮与压气机的功率平衡: (LTH-LcH)/LcH=0 (39) 低压涡轮流量平衡: (Wa22+Wfb-Wg45)/Wg45=0 (40) 低压涡轮与风扇的功率平衡: (LTL-LcL)/LcL=0 (41) 混合室入口内涵与外涵的静压平衡: (P5-P16)/P5=0 (42) 尾喷口的进口总压平衡: (43) 发动机部件模型和发动机共同工作方程共同组成了发动机的数学模型,发动机的共同工作点本质就是共同工作方程组的解。因此,发动机数学模型的求解问题就可以转换为对6个平衡方程所组成的非线性方程组求解问题。发动机非线性模型求解方法通常有牛顿-拉夫逊法和N+1残量法,本文选择牛顿-拉夫逊法求解该发动机数学模型: (44) 图2 发动机模型求解示意图 选择该型发动机正常暖机后中间状态的台架试车数据作为参考对象,将模型输入参数中的大气环境设置为台架测试环境,验证上述发动机模型的精度和准确性。将3台发动机台架数据和对应测试环境下的模型计算值进行对比,计算结果相对误差如表1所示。 表1 发动机中间状态模型计算值与实测值相对误差 % 从表1中可以看出,性能模型计算值与发动机实测值最大误差分别为5.26%、5.75%和4.91%,性能模型的最大误差在5%左右,符合一般情况下的建模精度要求。将表1中各性能参数的相对误差绘制如图3。 从图3中可以看出,3台发动机性能参数的相对误差分布基本一致,说明了所建模型的通用性。其中,大部分性能参数都是模型计算值大于实测值。这是由于在建模过程中进行了诸多假设,如:不考虑流道中气体与各部件之间的热交换,假设气体是完全气体且为一维定常流动等,使得模型的计算过程忽略了发动机实际工作过程产生的一些损失,因此,性能模型的计算结果普遍都偏大。燃油流量和涡轮后温度比实测值偏小,同样是由于计算过程忽略了实际工作中诸多损失,从而导致了性能模型可以用更少的燃油产生了更多的推力。 暖机与不暖机2种情况下发动机叶尖间隙会有所差别,不暖机情况下的叶尖间隙大于暖机后的间隙[1]。不暖机产生的间隙变化会直接导致发动机的部件特性发生变化,进而影响发动机的整机性能。 由于暖机与不暖机是针对飞机起飞过程产生影响,而起飞过程中发动机处于最大状态,因此,本文以发动机最大状态性能讨论暖机影响。 分别对3台发动机的暖机影响进行台架试车试验,获得发动机暖机与不暖机的性能数据。首先对发动机进行冷推,即发动机在启动后不暖机直接从慢车一路缓推到最大状态,得到不暖机的性能数据。然后将发动机油门收回,将发动机状态降到暖机状态进行暖机,暖机完成后再次将油门推到最大状态,得到暖机后的性能数据。用得到的台架数据进一步计算出暖机与不暖机性能偏差,计算公式为: (45) 式中:Yheating, j为发动机暖机后性能参数实测值;Yunheating, j为发动机不暖机性能参数实测值;j为发动机实测性能参数个数。将3台发动机暖机与不暖机2种情况下的最大状态性能实测值进行比较,并将不暖机实测值与模型计算值进行比较,其误差如表2、表3和表4所示。 表2 发动机A最大状态相对误差 % 表3 发动机B最大状态性能相对误差 % 表4 发动机C最大状态性能相对误差 % 从表4中可以看出,性能模型计算值与不暖机实测值相对误差较大。在发动机建模的过程中,暖机与不暖机2种情况下发动机的物理过程一样。但是,由于在建模过程中对发动机进行的诸多假设和简化处理,使得所建模型只能描述一个状态,这使得所建模型与真实发动机性能之间存在一些差异,不能描述暖机与不暖机本身存在的性能偏差,导致不暖机情况下模型计算值与发动机实测值相对误差变大,其最大相对误差分别为9.43%、9.54%和8.75%,此时原有发动机模型不能准确反映发动机的整机性能。 1) 正常暖机情况下发动机模型精度较高。以3台发动机的台架试车数据作为参考对象,将模型输入中的大气环境设置为对应发动机台架测试环境,对比发动机中间状态的模型计算值与3台发动机暖机后实测值,其最大误差分别为5.26%、5.75%和4.91%。性能模型的最大误差在5%左右,符合一般情况下的建模精度要求,验证了发动机模型的准确性。 2) 模型性能参数计算值与发动机不暖机实测性能相对误差较大。由于在建模过程中对发动机进行的诸多假设,使得所建模型与真实发动机性能之间存在一些差异,未能描述不暖机与暖机本身存在的性能偏差。不暖机情况下模型计算值与3台发动机实测值最大相对误差分别为9.43%、9.54%和8.75%,此时原有发动机模型不能准确反映发动机不暖机情况下的整机性能。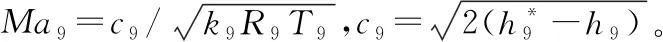

3 发动机共同工作方程


4 模型仿真与验证

5 暖机对性能模型的影响

6 结论
