毫米波大规模MIMO混合预编码优化交替最小化算法

王 婷，吴君钦

（江西理工大学 信息工程学院，江西 赣州 341000）

0 引言

未来无线通信网络预计实现1 000 倍信息容量的增长，因此无线网络的容量必须呈指数增长，才能满足高数据速率的需求[1]。通过大规模多输入多输出（MIMO）信道编码技术或通过缩小小区覆盖面积的方法，只能提高有限的系统容量[2]。当前蜂窝系统中的频谱紧缺是提升系统容量的主要问题，因此未充分利用的毫米波得到了研究者的广泛关注。毫米波的频谱范围为30～300 GHz，波长较小（1～10 mm），带宽可达到10 GHz，因此允许在收发器处配置大规模天线阵列用于提供较高的波束成形增益。另外，如果结合MIMO 技术合成高方向性波束可以降低毫米波产生的巨大路径损耗和降雨衰减。因此，可将其作为5G蜂窝系统中新频谱的主要候选[3]。但高硬件成本与高功耗使得毫米波系统无法像传统MIMO 技术为每一根天线配置单独的射频链路[4]。

为了解决该问题，近年来大量学者综合数字预编码和模拟预编码的特点提出混合预编码架构，通过移相器将高维模拟预编码与低维数字基带预编码相结合，可以大大减少射频链路数以及系统功耗，并保持较好的系统性能[5]。同时，毫米波系统的预编码结构设计可以分解为两个子问题，即预编码和解码问题[6]。而频谱效率的最大化可通过最小化最佳全数字预编码器和混合预编码器之间的欧几里德距离来近似[7]。这使得混合预编码器的设计问题成为具有移相器施加的单位模数约束的矩阵分解[8]。

针对上述特殊问题，在文献[7]中修改了毫米波大天线阵列的空间结构，将其转化为稀疏重构问题，并通过正交匹配追踪算法求解，降低了计算复杂度。然而这种限制模拟预编码可行空间集的解决方案，在简化单位模数限制的模拟器件设计的同时也会导致系统性能的损失，此外提前获取阵列响应向量的信息也会带来额外的开销。文献[9]中采用基于流形优化的交替最小化算法，称为MO⁃AltMin，其将单位模数成分嵌入复平面中的多个圆的乘积中，对数字预编码与模拟预编码进行嵌套循环更新，这种方法虽然提高了系统性能，但算法复杂且求解过程中涉及Kronecker 乘积，在大矩阵下具有极高的复杂度，因此无法在实际中应用。在此基础上，文献[9]中同时提出了通过引入数字预编码器的正交特性，使用提取相位来实现模拟预编码器更新的算法，称为PE⁃AltMin。然而，PE⁃AltMin 算法涉及矩阵的奇异值（SVD）分解，其计算复杂度会随着系统射频链路的增加而增加，频谱效率也会有所损失，属于一个次优方案。最后在文献[10]中不采用近似的欧氏距离，而使用基于梯度的方法直接最大化可实现频谱效率的方案，该方案在提高频谱效率的同时也具有很高的计算复杂度。因此在非凸的单位模数约束下，低复杂度高性能的混合预编码设计还有待进一步研究。

基于上述分析，本文提出了一种基于黎曼最陡下降（RSD）法的改进流形交替最小化算法（RSD⁃AltMin）。所提出的算法遵循交替最小化算法的基本思想，该算法不需要预先确定模拟预编码器的候选集，并使用FRF和FBB结合交替优化的单回路结构，解决了MO⁃AltMin 算法中FRF和FBB交替优化的嵌套循环结构而导致的收敛速度慢的问题。同时，改进梯度计算方法使用黎曼最陡下降避免了MO⁃AltMin 算法中Kronecker 乘积，从而有效地降低了算法的计算复杂度，并且拥有近乎全数字预编码的频谱效率。

1 系统模型

1.1 系统模型

考虑如图1 所示的单用户（点对点）毫米波MIMO 系统，其中，Ns数据流由Nt个发射天线发送和Nr个接收天线接收。发射器和接收器处的射频链数量分别表示为和，其中，Ns≤≤Nt和Ns≤≤Nr。因此，接收信号可以表示为x=FRFFBBs，其中s是Ns×1 具有的符号向量。

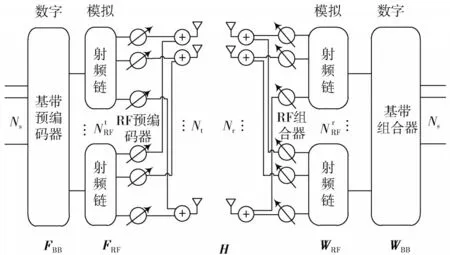
图1 毫米波大规模MIMO 系统混合预编码器

由于混合预编码器由一个Nt×模拟射频预编码器FRF和一个×Ns数字基带预编码器FBB组成，并施加归一化传输功率约束，即。因此，在窄带信道用户端经过解码器的接收信号可以表示为：

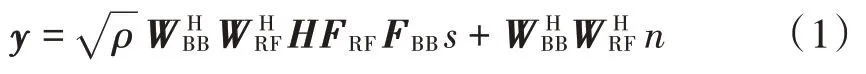
式中：ρ代表平均接收功率；H为信道矩阵；WBB是接收处数字基带解码器；WRF是接收处Nr×射频模拟解码器；n表示独立同分布（i.i.d）并且满足CN的噪声向量。为简单起见，假设发射机和接收机都具有完美信道状态信息。实际上，可以通过接收机处的信道估计准确有效地获得信道状态信息，并通过有效的反馈技术在发射机处进一步共享信道状态信息[11]。当传输符号遵循高斯分布时，可实现的频谱效率可以表示为：

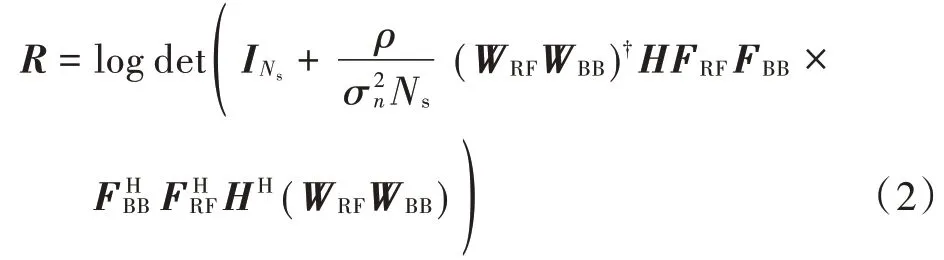
此外，模拟预编码器用移相器实现，移相器只能调整信号的相位。因此，FRF和WRF的所有非零相都应满足单位数模约束，即

1.2 信道模型

由于毫米波具有巨大的空间路径损耗和降雨衰减，其传播坏境的特征很好地体现在集群信道模型上，即Saleh⁃Valenzuela 模型。该模型将毫米波信道矩阵描述为：

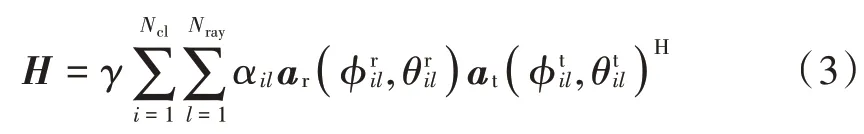
式中：γ=；Ncl和Nray表示簇的数量和每个簇中的射线数量；αil表示第i个传播簇中第l个射线增益，假设αil是独立同分布（i.i.d），遵循分布CN和这是满足=NtNr的归一化因子；另外，和代表接收和发射阵列响应向量，其中和分别代表信号到达和离开的方位角和仰角。考虑到的均匀正方形平面天线阵列（USPA）。因此将对应于第i簇中第l射线的阵列响应向量可以写成：

式中：d和λ分别是天线间距和信号波长，0 ≤p≤和0 ≤q≤是2D 平面中天线索引。虽然此天线阵列模型用于系统仿真，但所提出的混合预编码器算法也适用其他的天线阵列。

1.3 毫米波宽带正交频分复用系统

毫米波系统具有高损耗、高带宽的特点，而采用正交频分复用技术可以用于对抗毫米波系统中由于多径传播引起的快衰落，并且提高频谱利用率。因此对于宽带正交频分复用系统混合预编码的研究具有实际意义。

在传统正交频分复用多输入多输出（MIMO⁃OFDM）系统中（载波频率低于6 GHz），其混合预编码在频域内先对每个子载波进行数字预编码，再进行快速傅里叶逆变换（ITTF），最后再进行模拟预编码。这种特殊预编码方式也可以在宽带毫米波MIMO⁃OFDM 系统中使用，由于模拟预编码在ITTF 之后，而ITTF 操作会将所有的子载波信号组合在一起，所以在毫米波MIMO⁃OFDM 系统中所有的子载波信号只能共享一个公共的模拟预编码[12]。在这个限制下，系统解码后每个子载波的接收信号可以表示为：

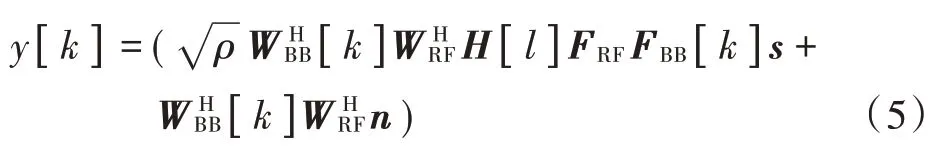
式中：k∈[0,K-1]是子载波索引；H[k]是第k个子载波的频域信道矩阵，表达式为：

式中：γ=是归一化因子；K是子载波总数。

2 混合预编码

2.1 问题描述

混合毫米波预编码器设计可以转化为频谱效率表达式最大化的问题，在文献[7]中指出，毫米波系统的频谱效率最大化可以近似转化为最小化混合预编码和全数字预编码器之间的欧几里德距离。相应的问题公式如下所示：

式中：Fopt代表最优全数字预编码器；无约束最优预编码和解码器分别由V和U的第Ns列组成，V和U是由信道的奇异值分解（SVD）导出的酉矩阵，即H=UΣVH；FRF和FBB是要优化的模拟和数字预编码器。

此外，用于减轻多径衰落影响的多载波技术正交频分复用系统的扩展问题公式可以定义为：

式中：L是子载波的总数；l∈[0,L-1]是子载波索引；FRF[l]和FBB[l]分别表示第l个子载波的最佳数字预编码器和基带预编码器。

2.2 算法描述

为了简化算法流程，首先介绍窄带毫米波系统。公式（7）本质可以看作矩阵分解问题，其涉及两个矩阵变量FRF和FBB，又因为FRF的所有非零元素都应满足单位数模约束，使得联合优化这两个变量变得非常复杂。交替最小化算法可以有效地解决以上问题，其核心思想为：在固定FRF和FBB的同时交替求解FRF和FBB。所提出的算法遵循交替最小化算法的思想，优化算法结构和改进梯度算法，具体算法如下：

受FRF上的元素单位数模约束，即，可将FRF的矢量化表示为vec(FRF)∈，形成复杂的倾斜流形OB(m,C)，具体表达式如下：

式中：m=注意OB(m,C)相当于m个复圆的乘积。因此，上述问题的表述变成了一个关于复杂斜流形和欧几里德空间的问题，在概念上被转化为搜索空间上无约束优化问题。由此，忽略式（7）被重新表述为：

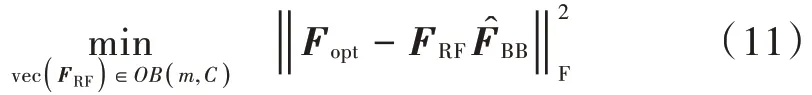
这种基于矩阵的G(FRF) 计算方法不同于依赖Fopt的矢量化和FBB的Kronecker 乘积的MO⁃AltMin 算法：

因此，梯度计算方式将基于Kronecker 乘积改变为基于矩阵相乘，大大降低了计算复杂度。接下来，通过将∇f(x)投影到切线空间TxOB(m,C)上，得到x处的黎曼梯度为：

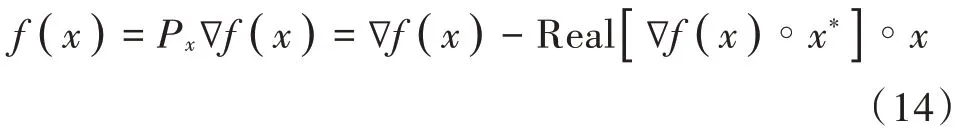
式中Px是投影到TxOB(m,C) 上的投影算子。最后，第k次迭代xk更新为xk+1=Rk(-αk ξk)，其中，αk是步长，ξk∈TxOB(m,C)是从梯度f(x)导出的方向，ξk的推导取决于所使用的算法，例如黎曼最陡下降和黎曼共轭梯度[13]。Rx:TxΜ→Μ:ζ↦Rx(ζ) 称为在x处的收缩，并将切线空间TxΜ映射到Μ上，具有一个局部优化条件，该条件保留了x处的梯度。这种情况使用循环结束后，通过将FBB=归一化为FBB，从而满足式（7）中约束的要求。

现在，通过式（11）进一步导出正交频分复用的宽带系统梯度计算扩展公式。相对于FRF的欧几里德梯度计算公式为：

基于上述，提出基于RSD 算法具体步骤如下：

输入：最优预编码器Fopt

步骤1：初始化x0；

步骤2：迭代次数k=0,1,2,…；

步骤3：将xk逆矢量化为

步骤5：使用式（12）计算欧几里德梯度∇f(xk) ；

步骤6：计算黎曼梯度ξk=

步骤7：找到步长αk，并更新xk+1=

步骤8：k=k+1，返回到步骤3；

步骤9：输出FRF=vec-1(xk+1) ；

步骤10：输出FBB=

此算法步骤适用于窄带系统也适用于OFDM 系统。值得注意的是，与MO⁃AltMin 算法相比，该算法中和FRF的更新是相互结合的，实现了算法的快速收敛。

3 复杂度分析

所提出算法需要计算式（12）中的欧几里德梯度，是影响算法计算复杂度的主要因素，而梯度计算复杂度为在文献[9]中所提出的MO⁃AltMin 算法，主要的计算复杂度在于式（13），公式涉及Kronecker 乘积，其计算复杂度为而PE⁃AltMin 算法由于其每次迭代都进行SVD 计算，其计算复杂度为综合以上复杂度分析，MO⁃AltMin 的计算对于大规模MIMO 系统来说复杂度极高，是所提出的RSD⁃AltMin 算法的十几倍。在高数据流及高射频数的计算复杂度所提出算法比PE⁃AltMin 算法低，在毫米波大规模MIMO 系统中具有实际价值。

4 仿真结果及分析

本节在毫米波大规模MIMO 系统中对所提出基于RSD 的交替最小化算法性能进行了仿真分析。仿真参数设置为：传播环境为Ncl=5 的簇环境，Nray=10 为每簇射线数，具有拉普拉斯分布的方位角、到达角和偏离仰角，平均角度均匀分布在[]0,2π 上，角度扩展为10°。实验假设L=128 的多载波情况，并且天线阵列以半波长距离分离，所以模拟结果使用平均超过1 000 信道实现。所有的实验都是在一台4.0 GHz、64 GB 内存的英特尔酷睿i7 电脑上用Matlab 编程实现。

为验证算法在低信噪比（Signal⁃to⁃Noise Ratio，SNR）下频谱效率的优越性，图2 将所提出的算法与MO⁃AltMin 算法、OMP 算法、PE⁃AltMin 算法和最优全数字预编码器在不同参数下进行了比较。

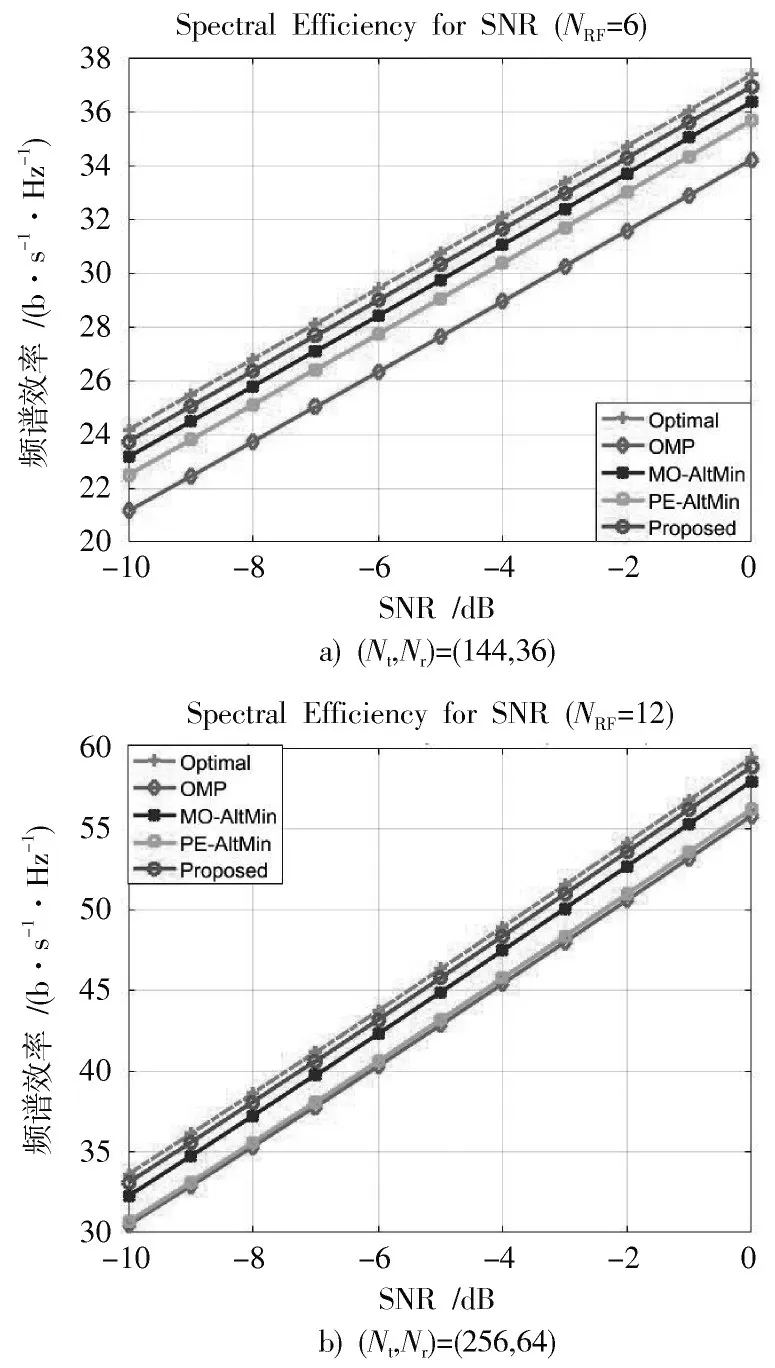
图2 相同信噪比下不同预编码算法频谱效率比较

图2a）显示出天线阵列数(Nt,Nr)=(144,36)时，射频链路数NRF=6、数据流Ns=4 时，相同信噪比下不同混合预编码方案所获得的频谱效率的比较。由图2a）可知，OMP 算法的频谱效率最低，MO⁃AltMin 算法与PE⁃AltMin 算法次之，而所提出的算法即使在射频链路有限的情况下也能够逼近最优的数字预编码器。图2b）将天线数设置为(Nt,Nr)=(256,64)，在保持数据流Ns=6，增加射频链路数NRF=12。由图2b）对比图2a）可看出，所有算法的频谱效率都有所提高，而提出的算法更接近最优数字预编码的频谱效率，这是OMP 算法、MO⁃AltMin 算法及PE⁃AltMin 算法无法实现的。

为进一步验证系统在高射频数下，系统性能的高频谱效率，图3 将提出的算法与MO⁃AltMin 算法、OMP 算法、PE⁃AltMin 算法及最优全数字预编码器在不同射频下的频谱效率进行了比较。

图3a），图3b）分别显示出了天线阵列数为(Nt,Nr)=(144,36)和(Nt,Nr)=(256,64)，在SNR=0 dB、低数据流Ns=6 时，不同的混合预编码的频谱效率随着NRF的变化情况。由图3 可以看出，PE⁃AltMin 算法、MO⁃AltMin 算法的频谱效率随着NRF数量的增加几乎没有得到改善，而OMP 算法由于简化单位模数限制的模拟器件设计，导致初始系统性能损失较大，但随着射频链路的增加，OMP 算法可以比PE⁃AltMin 算法的频谱效率更高。本文所提出的算法比上述三算法有着更好、更稳定的系统性能，随着NRF数量的增加，频谱效率在不断地接近最优数字预编码器。

图3 相同信噪比不同RF 数预编码算法频谱效率比较

图4设置天线阵列数为(Nt,Nr)=(256,64)，数 据流Ns=8 时，对所提出的算法与OMP 算法、PE⁃AltMin 算法及最优全数字预编码器在不同射频数NRF下算法处理时间进行了对比。此外，由于MO⁃AltMin 算法的处理时间是其他算法的几十倍，无法进行比较，将其忽略。

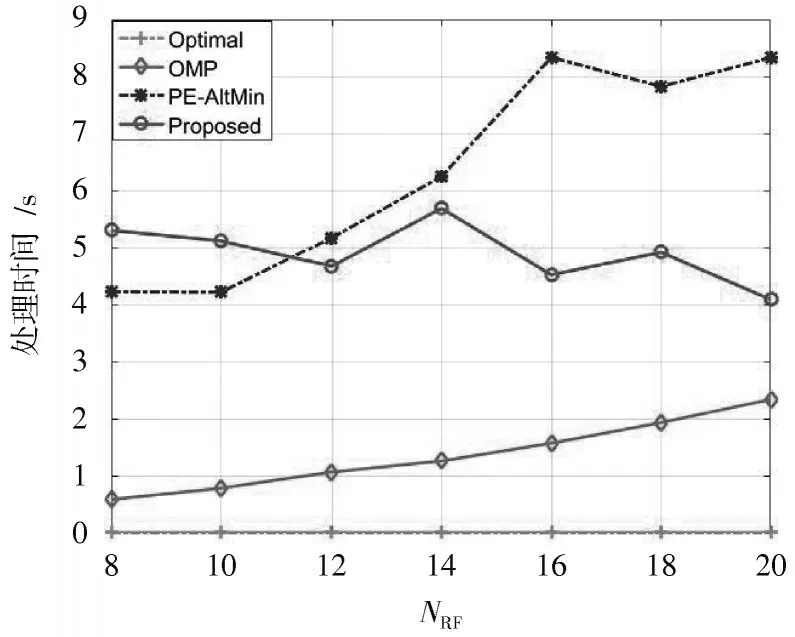
图4 不同预编码算法处理时间比较

由图4 可知，OMP 的处理时间最低，因为OMP 算法只需要进行基本的搜索，不需要进行迭代优化。在低射频数时，PE⁃AltMin 算法比所提出算法要低，而随着射频数的增加，PE⁃AltMin 算法的处理时间比所提出的算法要长，与文中上一节复杂度分析结论一致。在实际的毫米大规模MIMO 系统中，射频数不会太低，所以所提出的算法相对而言更具有优势。

5 结语

考虑现有的混合预编码设计方案的复杂度过高及系统性能损失较高，本文提出了基于RSD 的交替最小化算法（RSD⁃AltMin），使用数字预编码器与混合预编码器结合交替优化的单回路结构，避免了传统算法循环嵌套结构，加快了收敛速度。改进了梯度计算方法，使用RSD 法降低了计算复杂度。此外，考虑到实际应用，又将算法进一步扩展到采用正交频分复用的宽带系统实验。仿真结果表明，所提出的算法结构简单，计算复杂度远低于MO⁃AltMin，比PE⁃AltMin 算法有着更快的处理速度，系统性能高于现有的传统算法，更满足实际需求。未来可进一步扩展到多用户场景下的混合预编码系统中。