一种强干扰背景下间歇采样转发干扰抑制算法

李思文，王国宏，张 亮，张翔宇

（1.海军航空大学 信息融合研究所，山东 烟台 264001；2.中国人民解放军92635 部队，山东 青岛 266041）

0 引言

现代战争对雷达的电子干扰，通常利用干扰机完成。干扰机工程实现完全的收发隔离难度很大[1]，所以一般采用天线分时工作来避免收发自激。但是因为干扰机采用数字射频存储装置[2]（Digital Radio Frequency Memory，DRFM），会面临在完全读写时最小转发时延大于雷达脉宽，影响干扰效果。文献[3]为减小干扰信号转发时延并兼顾匹配性，设计了间歇采样转发干扰。干扰信号经雷达匹配滤波输出高密度相干假目标群，且部分假目标导前真实目标，欺骗兼压制雷达。间歇采样转发干扰有三种典型样式：直接转发（Interrupted⁃Sampling Direct forwarding Jamming，ISDJ）、重复转发（Interrupted⁃Sampling Repetitive Forwarding Jamming，ISRJ）和循环转发（Interrupted⁃Sampling Loop Forwarding Jamming，ISLJ）干扰，对其干扰特性分析和样式变种[4⁃5]的研究较多，干扰抑制研究相对较少。文献[6⁃7]通过识别来对抗间歇采样转发干扰，但在自卫式干扰条件下，干扰与真实回波时域完全重叠，即使辨别出干扰类型，仍需进行抑制处理。针对该问题，文献[8]利用分数阶滤波提取真实回波，但真实回波与干扰信号在最优阶次下仍有部分混叠，强干扰背景下恢复信号包含许多干扰分量，抑制效果不太理想。文献[9⁃10]从信号本身特性出发，利用真实回波和干扰信号分段脉压差异，设定干扰剔除门限消除部分干扰，然后再通过脉内、脉间积累实现干扰抑制，但算法基于经验确定干扰剔除门限，不合理的门限设定会导致过剔除或欠剔除，影响抑制效果。

针对上述问题，以自卫式干扰下LFM 脉冲压缩雷达抗三种典型间歇采样转发干扰为背景，提出一种强干扰背景下的干扰抑制算法。首先，根据不同参数构造ISDJ 参考信号，利用余弦距离最小准则估计干扰参数；其次，利用雷达发射信号和估计的干扰参数，设计两种线性正则字典，分别为正交字典和联合字典；然后，利用联合字典将回波细分为真实回波、干扰和噪声能量点，通过剔除干扰能量点，完成干扰信号初步抑制；最后，通过正交字典构造变换基，利用压缩感知算法从初步抑制回波中重构真实回波。

1 干扰切片特征分析

自卫式干扰下，设干扰机为点目标，不考虑回波时延[8⁃12]，真实回波零中频复数形式为：

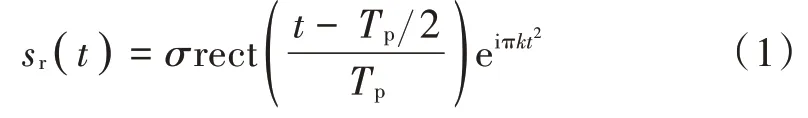
式中：σ为回波幅度；Tp为脉宽；k为调频斜率。根据间歇采样转发干扰产生方法，采样脉冲串[3]为：

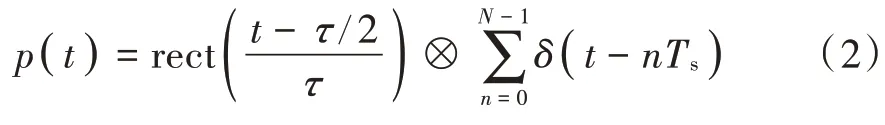
式中：τ为采样脉宽；Ts为采样周期；N=为采样脉冲个数。利用p(t)采样雷达信号，得到：

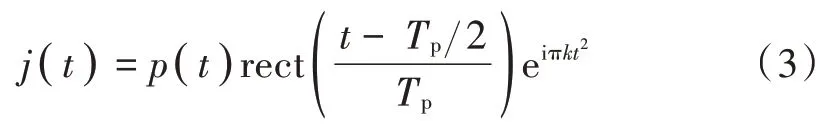
控制j(t)转发时延、次数，分别得到ISDJ、ISRJ、ISLJ 为：

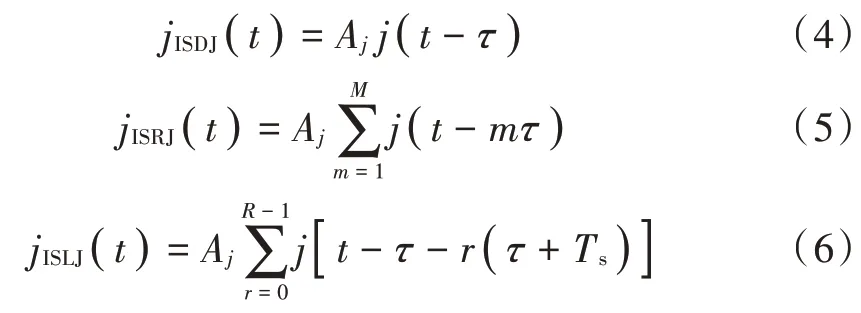
式中：Aj为干扰幅度；M，R分别为ISRJ、ISLJ 对j(t)的转发次数，M=R=min(M,N)，min(·)表示取最小值。图1对比真实回波给出了三种间歇采样转发干扰切片组合示意图，同样序号的切片信号形式一致。可以看出，干扰切片与对应的真实回波切片均为LFM 信号，调频斜率相同，初始频率不同，该差异可为干扰抑制提供依据。

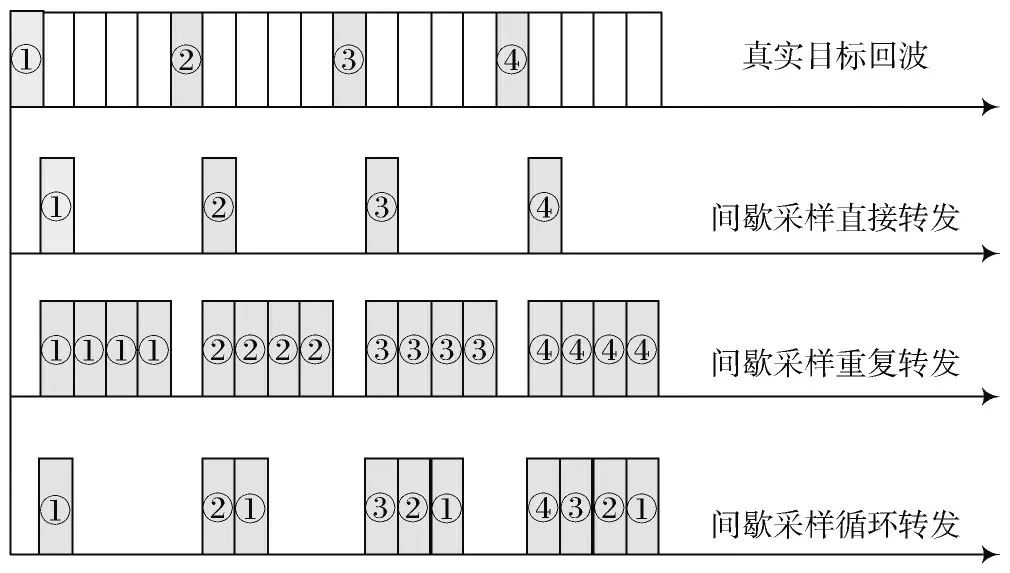
图1 切片组合示意图

2 干扰抑制原理

由第1 节可知，干扰切片与对应的真实回波切片存在初始频率上的差异，利用信号处理工具将回波切片变换为冲击函数（本文称其为能量点），分析受干扰回波能量点分布。线性正则变换（Linear Canonical Transform，LCT）作为分数阶傅里叶变换的广义形式，可使用LFM信号处理[11]。频率意义下，连续信号x(t)的LCT定义为：

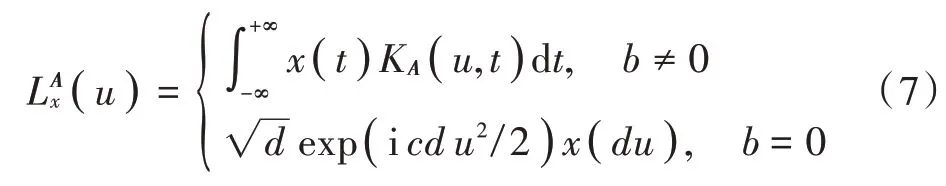
式中：A为参数矩阵，A=[a,b;c,d]，约束ad-bc=1，KA(u,t)为核函数，表示式为：

由文献[6⁃10]可知，真实回波脉宽Tp与采样周期Ts、采样周期Ts与采样脉宽τ存在整数倍关系，切片化真实回波可表示为：

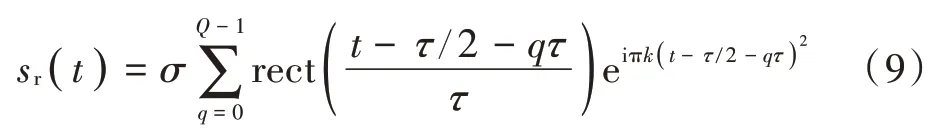
式中Q=为切片个数。令LCT参数=-k，将式（9）代入式（7）得到切片化真实回波LCT 为：

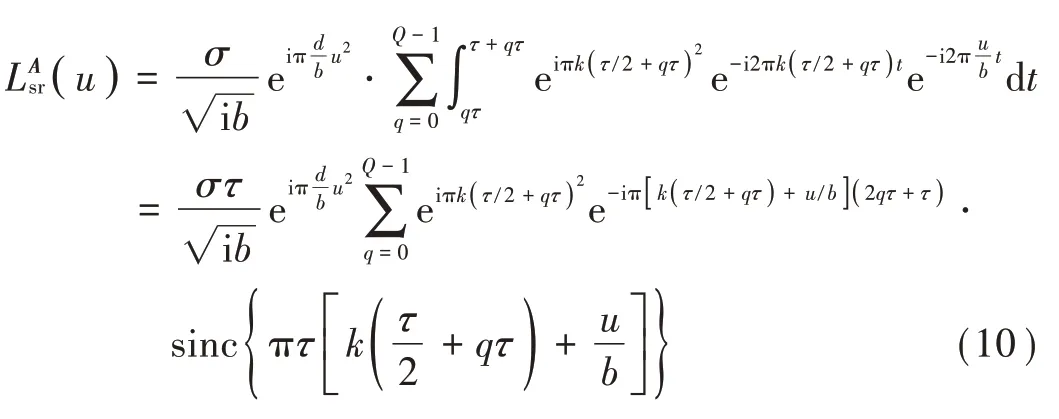
可以看出，切片化真实回波LCT 由Q个辛格函数组成，峰值均为对应LCT 域位置为：

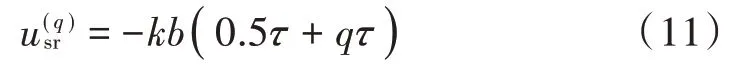
根据LCT 时移、频移性质[12]，容易得到切片化ISDJ、ISRJ、ISLJ 干扰LCT 表达式为：

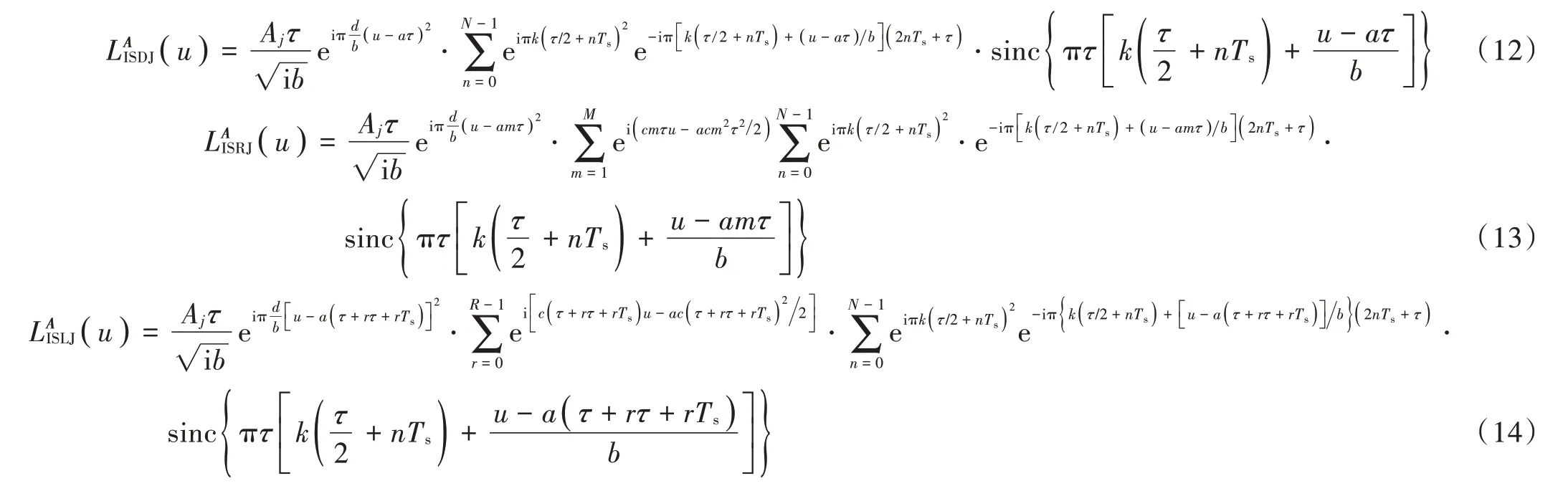
可以看出，切片化ISDJ、ISRJ、ISLJ 干扰LCT 分别由N，NM，NR个辛格函数组成，峰值均为对应LCT 域位置为：

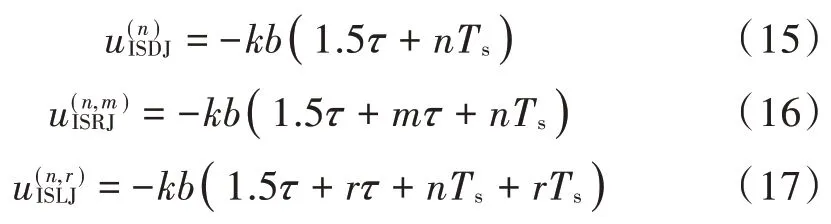
综合式（10）～式（17），图2 给出了切片化回波LCT示意图。可以看出，干扰能量点与真实回波能量点存在幅度和分布上的差异，剔除干扰能量点，即可实现干扰初步抑制，同时由于干扰能量点LCT 域位置与真实回波能量点位置不同，剔除干扰的同时不会破坏真实回波。经初步抑制，回波中的干扰分量大幅减少，构造合适的变换基，利用少量的观测值、观测矩阵，通过求解优化问题可高概率重构真实回波[13]。

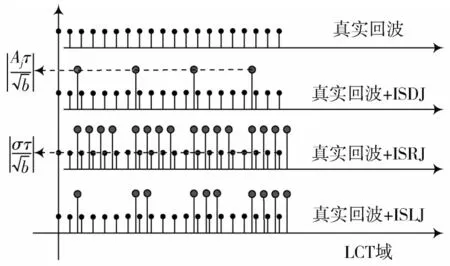
图2 切片化回波LCT 示意图

3 实现方法

第2 节在具体实现上有3 个问题需要解决：一是如何估计干扰采样周期和采样脉宽，以对回波进行切片化处理；二是如何得到切片化回波LCT，如何构造合适的变换基；三是干扰能量点的剔除规则如何确定。下面介绍具体实现方法。

3.1 基于余弦相似度的干扰参数估计方法

对于特定雷达信号，干扰采样周期和采样脉宽存在一定的参数范围。余弦距离（Cosine Distance，CD）常用于度量2 个向量余弦相似程度[14]。向量夹角越小，相似度越高，CD 值也越小。由式（5），式（6）可知，ISRJ、ISLJ 均可由ISDJ 线性表示，根据式（2）～式（4）构造参考信号，通过设定不同干扰参数，计算回波与参考信号CD，其最小值对应的参数即为干扰真实参数。

3.2 线性正则字典构造方法

文献[15]基于离散分数阶傅里叶变换核矩阵构造分数阶正交字典。本文利用Pei 型离散LCT 核矩阵[16]设计LCT 联合字典和正交字典，然后再利用LCT 正交字典构造变换基，具体步骤为：

步骤1：设计参数矩阵A，元素满足=-k，约束ad-bc=1。

步骤2：确定时域、LCT 域采样间隔Δt，Δu及对应采样点数2N+1，2M+1，对连续LCT 离散化处理，得到：

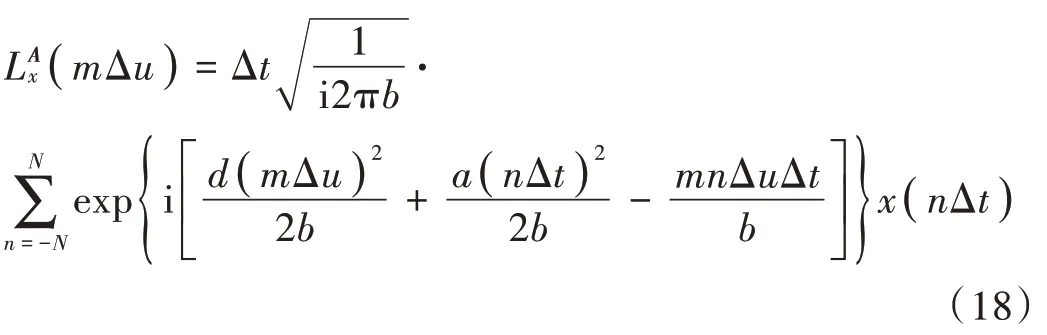
步骤3：式（18）可进一步表示为：

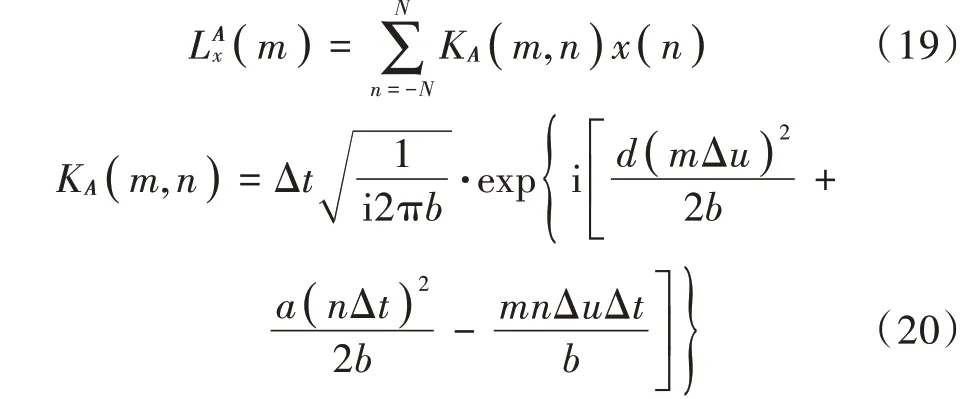
步骤4：为使KA(m,n)满足可逆性，要求：

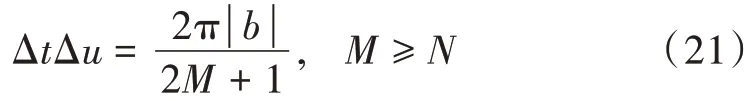
步骤5：将式（21）代入式（20），归一化处理得到：

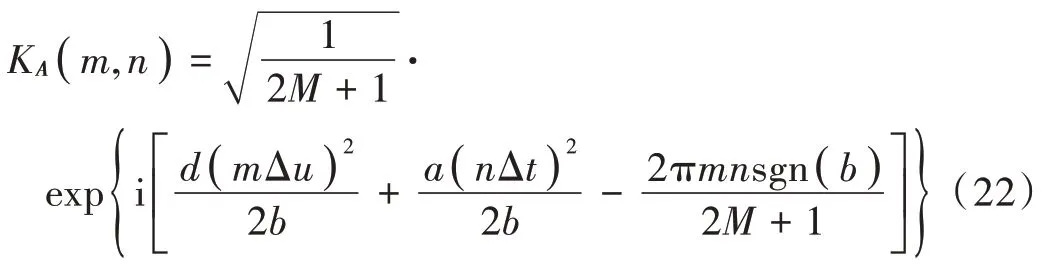
式中KA(m,n)即为LCT 正交字典，其共轭转置矩阵为重构真实回波时使用的变换基。根据3.1 节估计的间歇采样脉宽τ，确定时域、LCT 域采样点数，构造Q个正交字典，对角排列得到LCT 联合字典，计算回波信号在联合字典下的表示系数可得切片化回波LCT。

3.3 基于中位数绝对偏差的干扰剔除方法

为识别剔除干扰能量点，引入中位数绝对偏差（Median Absolute Deviation，MAD）。MAD 是一种较方差、标准差更为稳健的离差统计测量，常用于检测样本中的异常值。样本X的MAD 定义为：

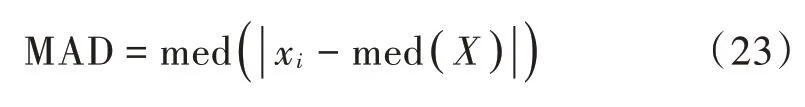
式中：med(·) 表示求中位数；xi为样本值。为提高MAD适用性，式（23）需修正为：

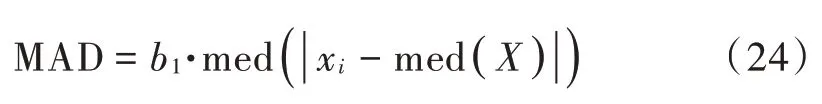
式中：b1为常数，b1>0，当样本服从正态分布[17]时，b1取值1.482 6。将切片化回波LCT 视为样本X，样本值xi满足式（25）则判定为干扰能量点。

综上所述，图3 给出了干扰抑制流程，该流程对ISDJ、ISRJ、ISLJ 均适用。

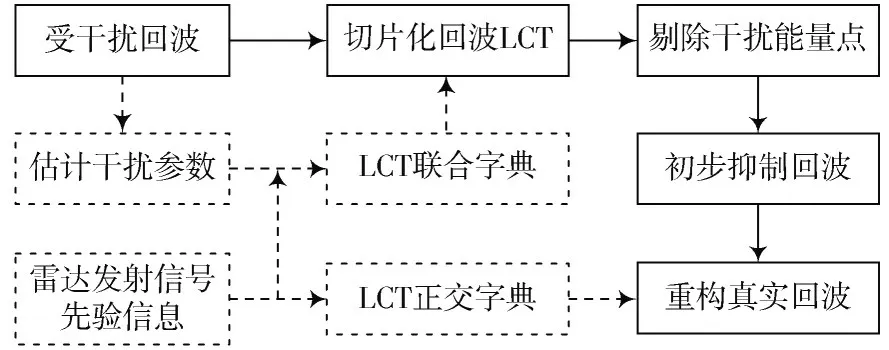
图3 干扰抑制流程

4 仿真结果与分析

4.1 参数设置

雷达发射信号为LFM 脉冲信号，脉宽80 μs，带宽10 MHz，采样频率20 MHz，真实回波幅度为1 V。间歇采样转发干扰采样周期为20 μs，采样脉宽为4 μs。图4由上至下依次给出雷达信号、ISDJ、ISRJ、ISLJ时域波形。

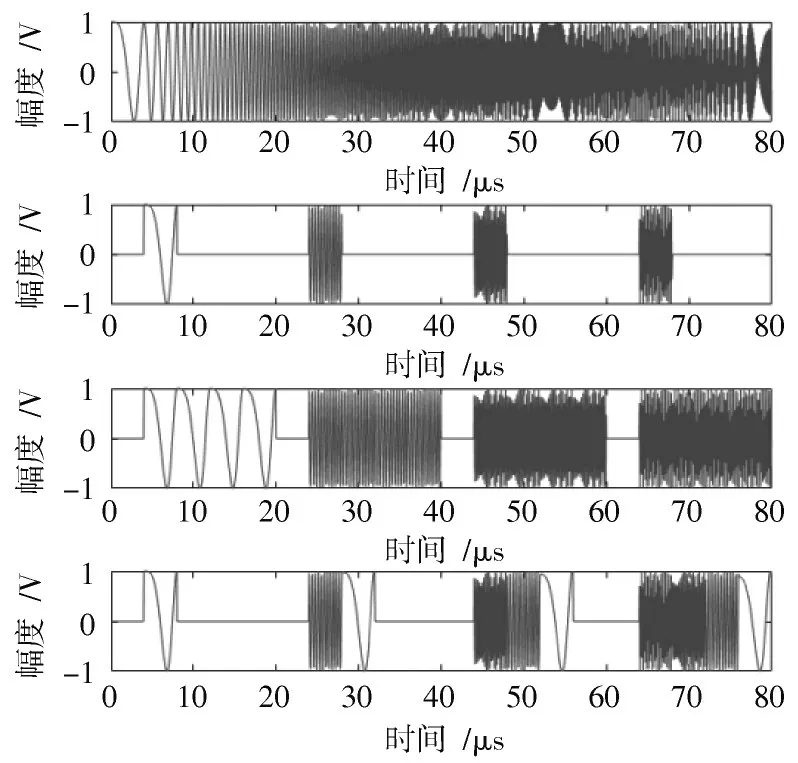
图4 干扰信号时域波形

4.2 算法可行性仿真分析

以抑制ISRJ干扰为例，设SNR为-5 dB，JSR为30 dB，搜索范围均为2～40，图5 给出了干扰参数估计结果，CD 最小值对应采样周期为20 μs，采样脉宽为4 μs，与仿真参数一致。

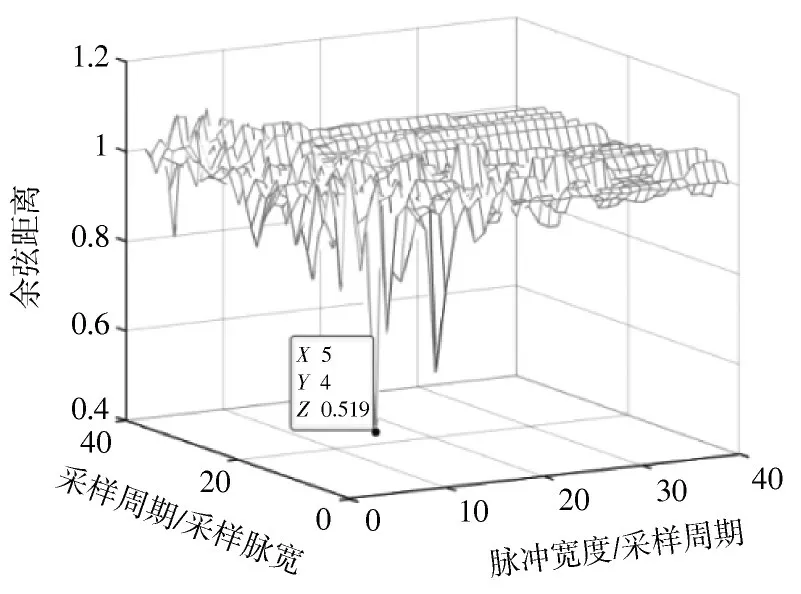
图5 干扰参数估计结果

利用3.2 节方法构造LCT 正交字典和联合字典，分别如图6，图7 所示。不同于LCT 正交字典，LCT 联合字典由20 个小字典对角排列而成，小字典个数与回波切片个数一致。

图6 LCT 正交字典

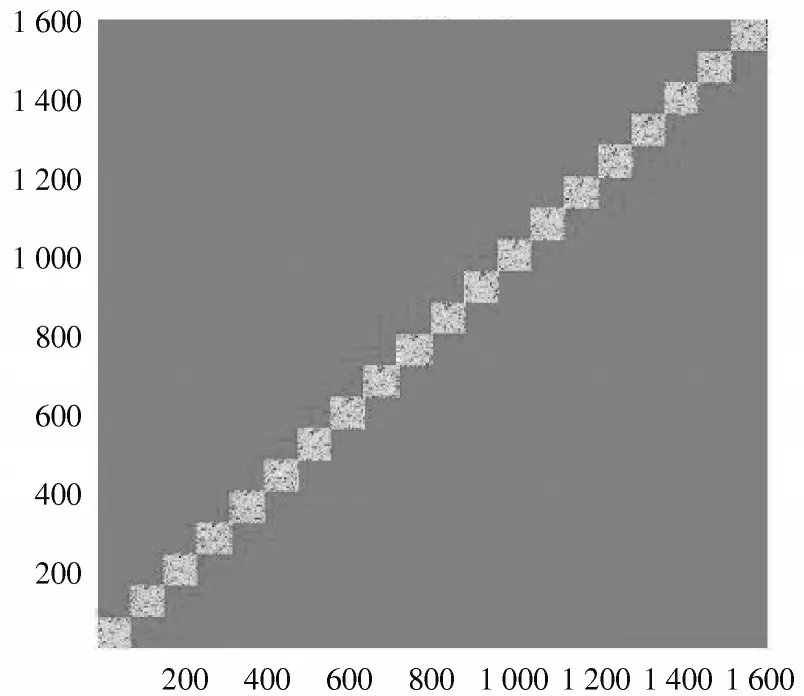
图7 LCT 联合字典

计算回波在联合字典下的表示系数，得到切片化回波信号LCT，如图8 所示。可以看出，强干扰背景下切片化回波信号LCT 存在明显的干扰能量点，干扰能量点个数与切片个数一致。根据3.3 节式（24），式（25）剔除干扰能量点，结果如图9 所示，对比图8 可知干扰能量点得到有效剔除。

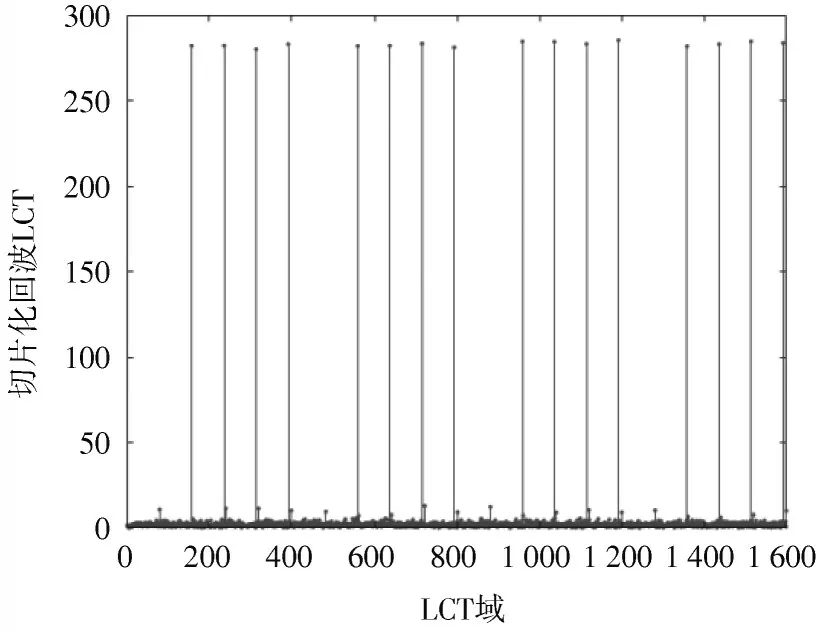
图8 切片化回波LCT

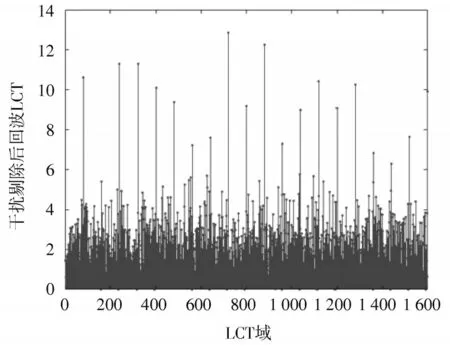
图9 自适应干扰剔除后切片化回波LCT

图10 给出了干扰剔除后回波时域波形，回波信号呈现LFM 特征。根据图6 的LCT 正交字典构造变换基，利用正交匹配追踪算法（Orthogonal Matching Pursuit，OMP）[18]从初步抑制回波信号中恢复真实回波，结果如图11 所示，恢复信号与真实回波高度相似。

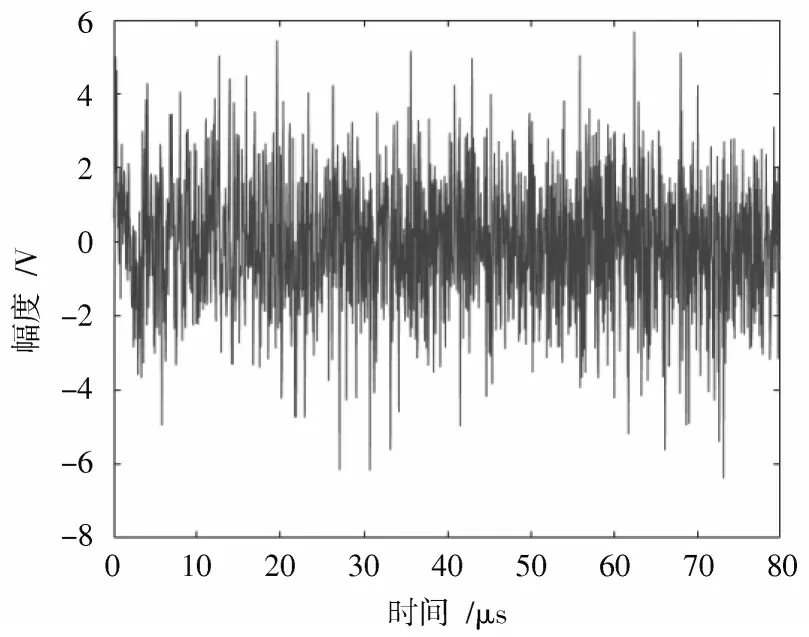
图10 自适应干扰剔除后回波信号

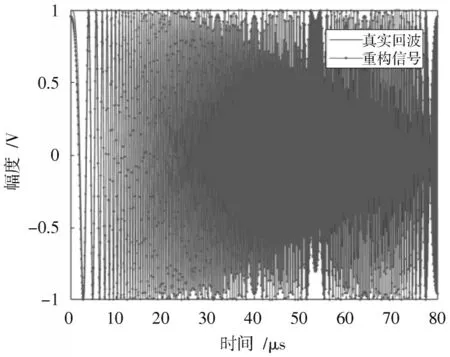
图11 真实回波重构效果

4.3 算法效能分析

为评估余弦距离最小准则干扰参数估计效能，定义干扰参数估计准确率（Jamming Parameters Estimation Accuracy，JPA）为：

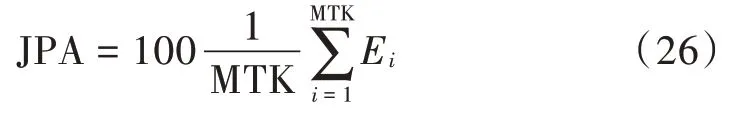
式中：JPA 的单位为百分比；MTK 为蒙特卡洛次数。若估计的干扰参数与真实参数一致，令Ei=1，否则Ei=0。设SNR 为-5 dB，JSR 取值为15～60 dB，间隔1 dB，运行蒙特卡洛仿真500 次，图12 给出了JPA 随JSR变化曲线，不同JSR 条件下JPA 均接近100%。

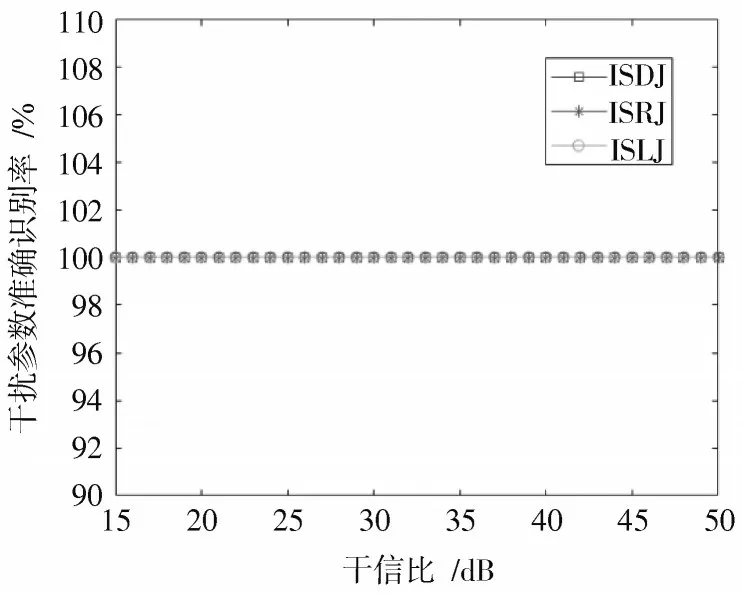
图12 JPA 随JSR 变化曲线

分析算法对三种间歇采样转发干扰抑制程度，定义平均干扰抑制率（Mean Suppression Rate，MSR）为：

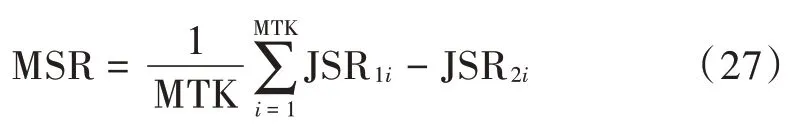
式中：JSR1i为第i次蒙特卡洛抑制前干信比；JSR2i为抑制后干信比。SNR、JSR、蒙特卡洛次数同上，图13 给出了MSR 随JSR 变化曲线，不同JSR 条件下，所提算法对三种间歇采样转发干扰均能达成一定干扰抑制效能，且对不同干扰样式抑制程度相差不大。同时可以看出，MSR 与JSR 近似呈线性关系，说明算法能够较好地适应JSR 变化。

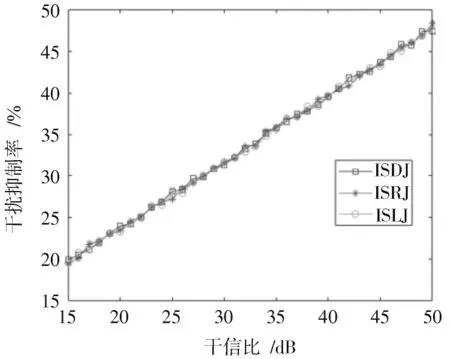
图13 MSR 随JSR 变化曲线

5 结语

间歇采样转发干扰由雷达信号切片拼接而成，不同拼接方式生成不同的干扰样式。本文利用干扰切片与真实回波切片初始频率差异，提出一种基于LCT 字典的间歇采样转发干扰抑制算法，算法基本思想是将回波区分为真实回波能量点和干扰能量点，通过剔除干扰能量点，完成干扰初步抑制，再利用压缩感知算法重构真实回波。仿真结果表明，所提算法能够有效抑制强干扰背景下的三种间歇采样转发干扰样式，从干扰参数识别准确率、干扰平均抑制率2 个指标验证了算法效能。