最优覆盖校内巡逻车配备方案及其评估模型
2021-08-06王泽松王梓天万后鹏秦泽青
王泽松,王梓天,万后鹏,秦泽青
(1.湖北大学计算机与信息工程学院,武汉430062;2.湖北工业大学计算机学院,武汉430062)
1 问题分析
我们以某校为例,考虑该校的实际情况,同时假设该校突发事故发生现场均在图1的道路上。该校三个重点部位的坐标分别为:(5112,4806)、(9126,4266)、(7434,1332)(见图1红点部位,蓝色部分为水域,相邻两个交叉路口之间的道路近似认为是直线)。

图1 数据生成全景图
该校拟增加一批配有先进通讯设备的校园巡逻车。假设学校内校园巡逻车的平均速度为15Km/h,遇到紧急事故开往事故现场的平均速度为30Km/h。校园巡逻车配备及巡逻方案要尽量满足以下要求:
D1:校园巡逻车在接到校园报警电话后四分钟之内赶到现场的不低于90%;而赶到重点部位的时间必须在三分钟之内。
D2:使巡逻效果更显著。
现需要建立数学模型解决以下问题:
(1)若要求满足D1,该校最少需配备多少辆校园巡逻车?
(2)请给出评价巡逻效果的评价指标,并给出满足D1且尽量满足D2条件的校园巡逻方案。
(3)你认为还有哪些因素、哪些情况需要考虑?给出相应的解决方案。
对于如何求在满足D1条件时,校园所需配备巡逻车的最少数量,我们可先将路口与道路信息从坐标轴中提出,转化为带权无向图结构,用节点表示路口,边表示道路,各边权重则代表着道路的长度。针对要求D1,我们通过时间与巡逻车速度的信息,将对时间的限制变成了对距离的限制,从而,问题一的概念发生了如图2的改变。
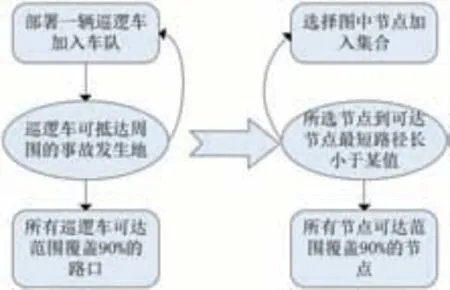
图2 概念转化图
接下来,我们所需解决的,也就是“找到最少节点集,其可达覆盖至少90%的节点”的问题。为了使巡逻效果更显著结合我们对巡逻车在实际工作中工作方式的理解,在巡逻效果的评估上,我们给出三个参考因素。
(1)整体覆盖率
我们认为首先应该提及的就是巡逻车队整体的作用覆盖率。这是由于巡逻路径对整体作用范围的影响是直观的,故整体的覆盖率可以直接体现一套巡逻方案中,策划者对巡逻路径所作安排的优劣。
(2)应答时效
鉴于事件的发生方式完全随机,我们优先考虑极端情况,即突发事件发生时,巡逻车到达事发地点所需行驶的距离达到巡逻路径上的最大值,并将此时巡逻车赶到事发地点的用时记作应答时效tmax,我们认为该数值可以反映巡逻方案对极端紧急情形的应对能力。
(3)巡逻路径长度
基于节能环保,倡导绿色生活的宗旨,我们希望在满足需求的情况下,巡逻车消耗最少的电量,即行驶最短的距离,因此,将巡逻路径的总长度纳入考虑因素,其可以反映巡逻方案在节能上的作用效果。在三项参考因素的基础上,我们根据各因素的重要性为其分配权值,并融合得到评分指标γ。
2 模型的假设
根据本文提出的问题和以上的问题分析,我们做了如下模型假设:
(1)在问题一中,假设巡逻车的位置均位于交叉路口。
(2)在问题一中,假设重点部位等不在道路上的点近似到最近的交叉路口及道路上。
(3)在问题一中,经计算,图中两交叉路口间连线距离小于2000m的概率为99%(4分钟内均可到达),故假设面积覆盖率等价于交叉路口的覆盖率。
(4)在问题二中,假设巡逻车在处理事故时耗费时间为无穷大,且事件总并发数小于等于巡逻车数量。即巡逻车到达事件处理地点后不可移动,仅能解决当前位置的事故。
(5)在问题二中,对于巡逻车路径的移动我们假设在同类型的区域内从一个交叉路口移动到另一个交叉路口的时间相同,且由于不同区域之间距离较远,从效率角度假设巡逻车不会跨区域进行巡逻。
3 符号说明
本文常用符号见下表,其他符号见文中说明。
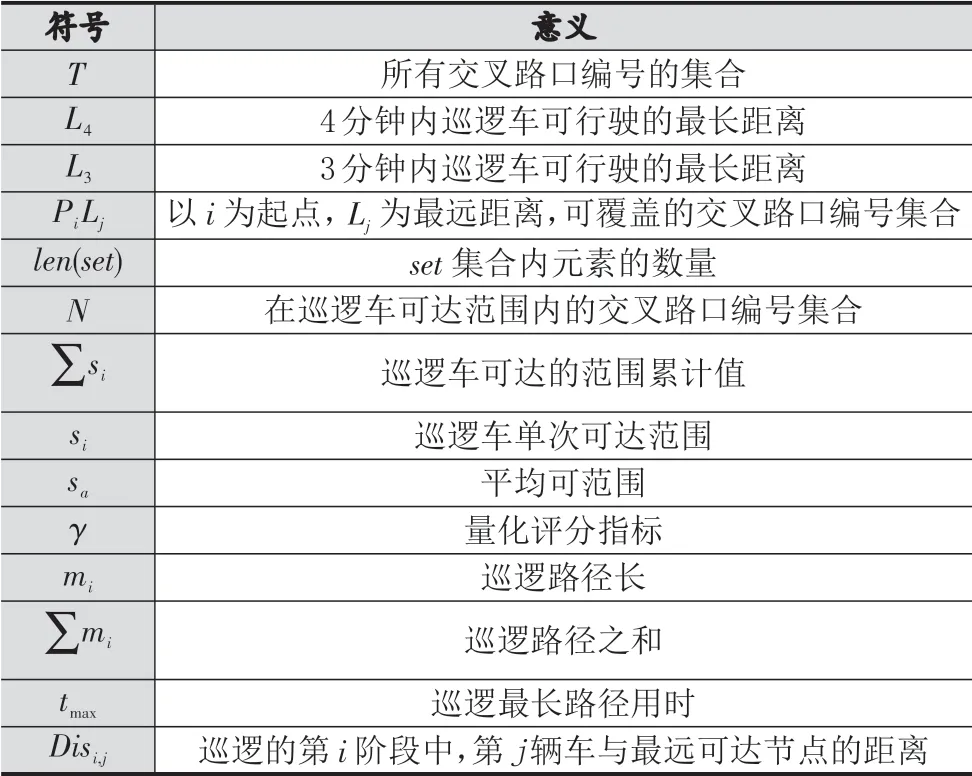
表1
4 模型的建立与求解
文献[1]中利用了退火算法进行路径优化调度,文献[2]基于博弈论对巡逻策略展开了研究。不同于它们,本文采用蒙特卡洛算法进行模拟巡逻轨迹,并结合图论算法达到模型的自优化效果。
4.1 问题一的建模与求解
问题一中需要求出满足D1条件时,需要部署的最少巡逻车数目,为解决该问题,我们使用蒙特卡洛法与弗洛伊德法,建立了最小消耗覆盖模型。本小节的主要内容是最小消耗覆盖模型的建立、模型的求解与分析、问题一的回答。
(1)最小消耗覆盖模型的建立
本模型主要采取了“覆盖”的思想,通过将路口与道路信息转化为图,进而把4分钟内“赶到现场不低于90%”转化为“4分钟内巡逻车活动覆盖面积大于校园的90%”。在求解最小巡逻车数目的过程中,利用蒙特卡洛模拟算法来随机模拟巡逻车的初始位置,再通过使用弗洛伊德算法求出任意两节点间的最短路径,可以得到每辆巡逻车可覆盖的面积,经由假设3,巡逻车可达面积的覆盖率可等价于巡逻车可达交叉路口的覆盖率,单次蒙特卡洛模拟的简化流程如图3所示。
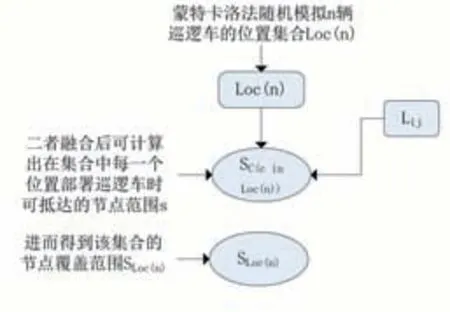
图3 单次蒙特卡洛模拟的简化流程
蒙特卡洛算法在大规模的随机数列与复杂系统中的模拟有着杰出的表现,例如在电力系统中的评估[3-4]、水质概率预报[5]、证券定价[6],等等。因此,我们认为其模拟的巡逻车初始位置与真实环境具有高度相似性。
在蒙特卡洛模拟过程中,为得到最小且符合要求的巡逻车数len(N),我们还需要加上约束条件:
①四分钟之内赶到现场的不低于90%:
以4分钟内巡逻车可以行驶的距离为度量指标,利用弗洛伊德算法计算每辆巡逻车可以覆盖的交叉路口数,使覆盖总数大于交叉路口数的90%。
②重点部位的时间必须在三分钟之内赶到:
以三个重点部位为圆心,以内巡逻车可以行驶的距离为度量指标。分别计算三分钟内可以到达这三点的交叉路口集合,最终巡逻车的位置应该包含这些集合中的点。
(2)模型的求解与分析
①计算方法的设计
在求解最小消耗覆盖模型时,我们首先将约束条件转换为公式表达:
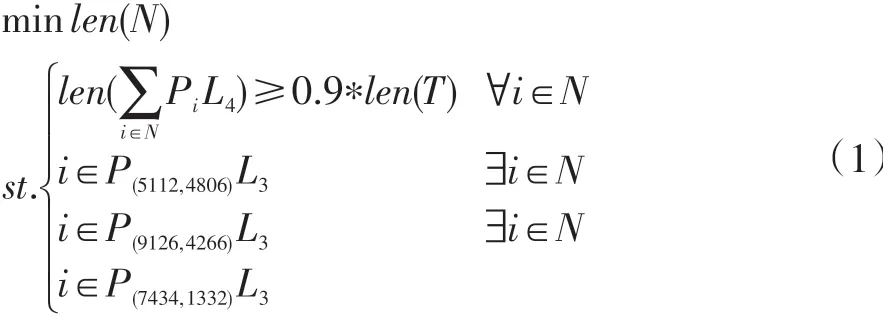
基于建模过程中提到的单次蒙特卡洛模拟,我们将其结合弗洛伊德算法,应用在图结构上,并写出完整算法,如图4所示。
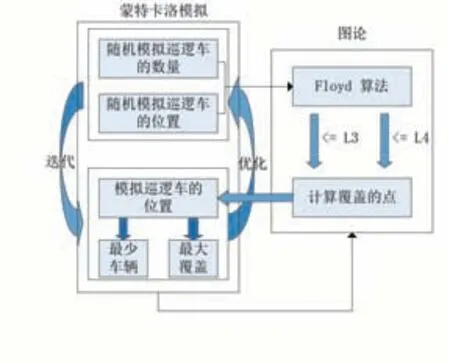
图4 问题一算法流程图
单辆巡逻车的覆盖范围的计算如表2所示。
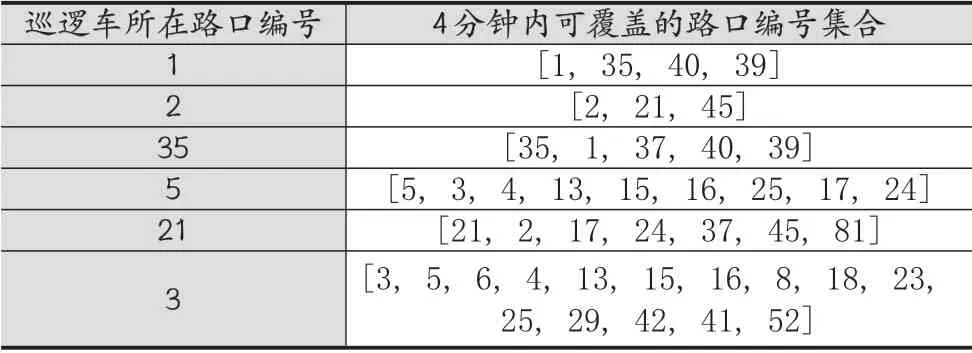
表2 单车辆覆盖范围示例
由于约束条件的存在,我们需要针对三个重点检测地进行特别处理,从3分钟内可覆盖它们的节点中进行单独选取,以保证模拟的巡逻车位置能满足条件,及时赶到重点地点。可及时抵达三处重点检测地的节点编号集合如表3所示。
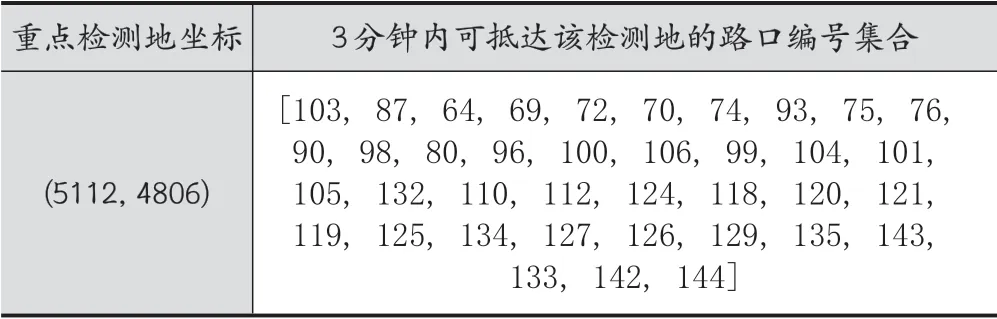
表3 可及时抵达重点检测地的路口编号集

续表
②结果分析
最终,所用车辆最少时,巡逻车所在交叉路口的编号分别为[140,94,40,290,137,261,217,49,12,260,250,25,105,213,180,43,300,10,305,116,8]。此时蒙特卡洛模拟结果如图5所示。图中,红色的点代表巡逻车所在的位置,红色加绿色是紧急情况发生4分钟内能覆盖到的范围,由图可见,21辆巡逻车的覆盖范围大于90%,且可在3分钟内前往重点地段。
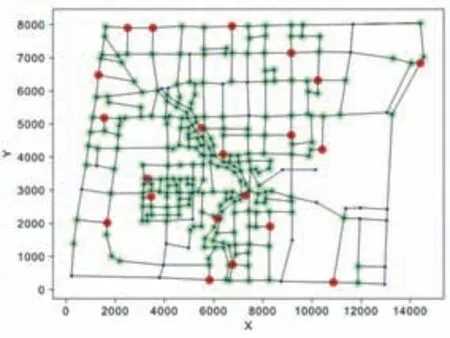
图5 最终蒙特卡洛模拟结果
③问题一的回答
经计算得出,满足要求D1时,该校最少需配备21辆校园巡逻车。
4.2 问题二的建模与求解
问题二要求给出评价巡逻效果的评价指标,并给出效果显著的巡逻方案。结合我们对问题二的分析中提出的影响因素,我们建立CTL模型来帮助我们评价巡逻效果,进而计算出一个可供方案间比较的评分数值,择出分数最高的巡逻方案进行选用。本小节的主要内容为CTL模型的建立、模型的求解与分析、问题二的回答。
(1)CTL模型的建立
在问题二的分析中我们已经提到需要考虑的三个影响因素,C(整体覆盖率)、T(应答时效)、L(巡逻路径长度),在它们的基础上,我们构建CTL模型来对巡逻方案进行评估,求解评分数值γ。
下面给出C、T、L的定义与推导:
C:整体覆盖率
根据不同点间平均路径的差异,我们将巡逻点分为不同的区域。基于假设5,我们可知相同区域内巡逻车是同时移动的。每当所有巡逻车到达新的交叉路口时,记录下当前的三分钟内所有巡逻车可达位置的范围si,取多次范围si求和。
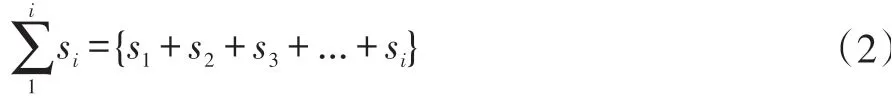
利用∑1i s i,对巡逻方案中不同阶段的s i求均值得到该巡逻方案的平均覆盖范围s a,同时对于巡逻车的位置进行多次重置,回到起始点,且巡逻车每次从相距自身最近的三个交叉路口中选择一个作为下次访问的路口,保证计算的范围具有普适性。

我们用区域里覆盖范围内交叉路口数除以本区域内所有路口数Ta作为整体覆盖率。
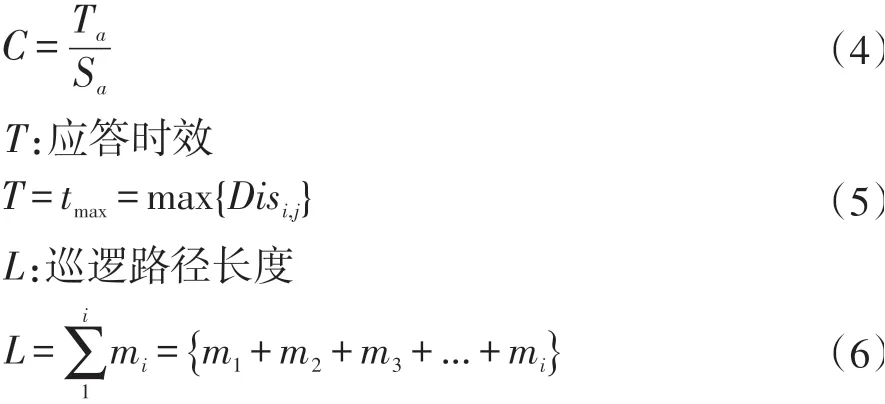
为找出三种因素中的在评价过程中的重要性关系,我们利用AHP层次分析法对这三项指标进行分析,进而得到定量的评价指标γ。
在拥有评价指标后,我们继续使用蒙特卡洛模拟不同的巡逻方案,从中选择覆盖率高于90%,且γ值最小的方案。
(2)模型的求解与分析
依据节点间平均距离的差异,我们将地图分为两块区域,如图6所示。区域1代表低密度区域,也就是正方形区域,区域二代表高密度区域,也就是三角形区域。
在对三项指标进行AHP分析之后,得到的判断矩阵如下:

对矩阵进行一致性检验,我们得到了指标情况CR<0.10,所以该判断矩阵A的一致性可以接受,同时我们使用算术平均法求得权重。

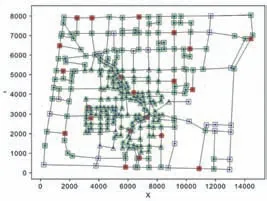
图6 分区
根据计算的结果,我们得到定量的评价指标如下:
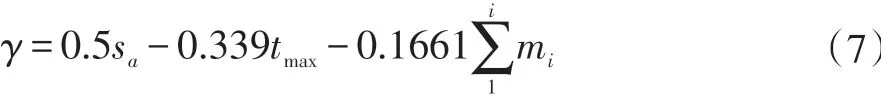
将各参数的值进行归一化后代入计算我们就能得到量化的巡逻效果评价指标。
我们利用蒙特卡洛法进行了1000000次随机模拟,每次巡逻车随机移动至与当前路口相邻的路口,我们控制每个区域里的覆盖率大于90%,且γ值最小,计算出了最佳巡逻方案,在最佳方案下,两区域的评分与覆盖率如表4所示。

表4 计算结果
(3)问题二的回答
我们使用经由CTL模型生成的γ作为方案评价指标,并给出在此指标下表现最优的方案。
4.3 问题二的分析与求解
在前两问的分析中,我们认为巡逻车处理事件的用时为无穷大,由此避免了某一巡逻阶段中,单巡逻车处理了多个突发事件的情形发生;同时我们也假设了,事件总并发数不超过巡逻车数目,且仅会发生一次,解决后不再复发,从而将情况控制在了巡逻车可处理范围内。然而在实际维护治安的过程中,处理治安事件的时间不一定为无穷大,往往巡逻车赶到目标地点后,仅花费短暂时间即可解决事件并离开;事件并发数目也不总是如我们所愿,以至于巡逻车能轻而易举地摆平校园内的所有突发事件。
(1)对于不同用时事件进行分类处理
在考虑到巡逻车处理用时不总为无限长后,我们对事件的类型进行分类分析,对于少部分处理事件所需时间为无穷的事件,我们采用之前的分配方案,同时对于在短时内可以处理的事件我们则需对其进行新的优化处理。
为了便于分析,我们假设事件分为两种,一种事件处理时间为无限长,巡逻车到达事件发生地点后无法移动。第二种事件处理事件为无限短,即认为巡逻车到达后事件即解决,巡逻车可立即前往一下事发地点。同时我们认为不同类型的事件发生时应存在某种特定比例。
我们用以下的情形来模拟:
车辆总数不变记为n,并发事件数q等于车辆总数也为n,当事件并发时每次出现的处理时间无限长事件数ql占全部事件数的一半,当总数为奇数时,ql向下取整。全部事件解决后车辆重新分布规划,随后发生新一次事件并发。我们意图展现出在事件过量发生时整个系统具备的稳健性,我们记录下每一次并发后所有事件解决的总范围并要求在问题1的要求下的总巡逻范围至少要达到总面积的60%,并以此分析出在车辆不足场景下巡逻轨迹以及巡逻点的生成规律是否受到影响。
(2)对于高事件并发数情形的应对
在前两问的背景下,事件发生的次数我们认为不超过巡逻车辆数,并且再一次发生后事件不再更新。实际上事故可能会不断发生,于是我们认为事故每隔一段时间会继续发生,直至超过巡逻车可以处理的最大值。由于事件的并发数的失控,我们需要容错率更高的部署方案,因此,巡逻车不再只部署在各交叉路口,将其转移到事故多发地的中心加以应对,如此,巡逻车在解决事件后可迅速赶往下一处事件发生地。
我们首先将所有事件发生地点进行聚类,把各簇中心视作事件发生地。同时由于簇中心数显著小于车辆总数,车辆可根据簇的密度前往各聚类中心。每当一次事件解决完成后,重新进行一次聚类过程直至所有的事件决完成。相较于前两问的情况,此情况下事件发生的位置处于动态变化之中,需要对车辆的运动过程进行实时的分析。鉴于我们单次并发产生的事件数较少,经多次实验,我们发现使用Mean-Shift算法可以得到最好的聚类效果。我们以轮廓系数作为标准评价几种分类算法,轮廓系数定义如下:
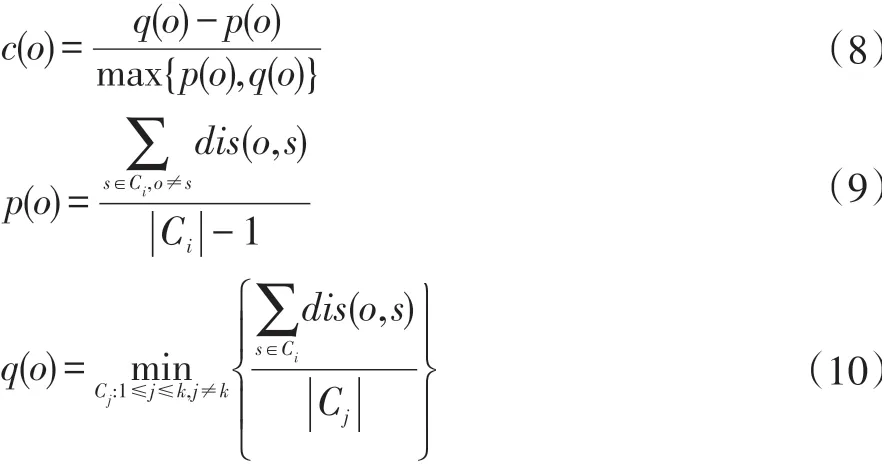
式中:
O代表C i中的对象,p(o)代表o与C i中剩余对象的均值,q(o)代表o与Ci中其他点的平均距离,c(o)代表O的轮廓系数。
最终公式如下:

各聚类方法效果如表5所示。
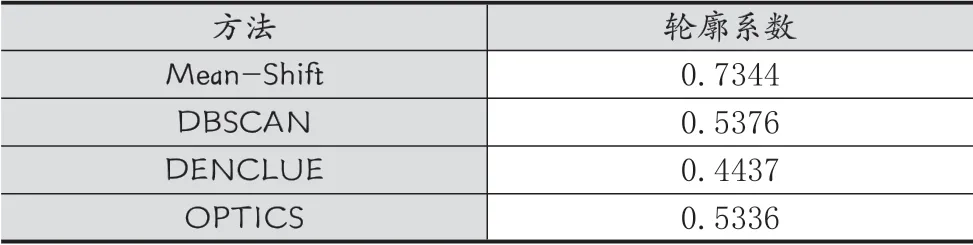
表5 各聚类方法效果
5 模型的评价与推广
5.1 模型的优点
针对问题1:
我们结合了蒙特卡洛模拟和图论中的弗洛伊德算法,用蒙特卡洛算法模拟巡逻车的初始位置与数量,以弗洛伊德算法求得的最短路径为指标计算巡逻车在不同时间段内可覆盖的最大范围。最终生成了巡逻覆盖图清晰且直观地展现了采取本策略可达到的预期成效。
针对问题2:
由于在实际的巡逻过程中,车辆处于运动状态。我们选取了整体覆盖率、应答时效和巡逻路径这三个方面作为优化巡逻路线的三个评价指标并采取了层次分析法对其进行了附权。我们依照路口密度将校园进行了分区并求解最优,最终校园百分之九十以上的路段都会被巡逻到,发生紧急情况时可做到全覆盖。
针对问题3:
为了设计出更符合实际场景的巡逻过程,我们将巡逻过程进行了两方面的扩充,首先将巡逻处理的事件种类做了扩充,此外还考虑了事件并发的重复过程,使得整个模拟环境由静态转为动态。最终我们发现在这样一个动态模拟的环境下,需要优先对生成的数据进行聚类分析,经多次实验我们找到了聚类效果最好的Mean-Shift算法,实现了动态分析最优巡逻路径。
5.2 模型的缺点
针对问题1:
部分路口之间的距离大于2000,在求覆盖率时忽略了这些细微因素的影响,直接用交叉路口的覆盖率代替了面积覆盖率。
针对问题2:
层次分析法附权带有稍许主观色彩,在有真实数据支撑的情况下可以用熵权法来修订参数。
针对问题3:
由于事件并发数数量的限制,聚类算法分析结果的可靠性有待提升。
5.3 模型的推广
本模型可用来指定校园巡逻策略,可以通过图的形式清晰直观地展示成效。同时随着评价体系的建立,本模型可对校园已经采取的巡逻策略进行评估,便于后期的改进。同时本模型还考虑了在处理事件类型不同且事件多次并发情况下的巡逻路径分析策略,可为不同的事件提供不同的方案,通过在不同条件下及时进行对路径的调整得到最佳的动态巡逻策略。
