例谈如何使题目的设问更自然
2021-08-05付军
付 军
(安徽省六安皋城中学 237000)
笔者是初中的一名数学教师,近日在陪同初三学生学习的过程中,遇到了这样一道题目,通过教学中学生的探究与作答,与出题人给于的参考答案进行对比,发现了一些问题,引发了笔者的一些思考.
一、原题重现
例1 (浙江省宁波市中考题)若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.

(1)已知△ABC是比例三角形,AB=2,BC=3,请直接写出所有满足条件的AC的长;
(2)如图1,在四边形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAC=∠ADC.求证:△ABC是比例三角形.
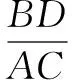
二、参考答案重现
解(1)因为△ABC是比例三角形,且AB=2、AC=3,
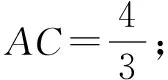
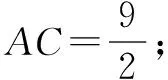
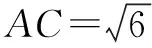
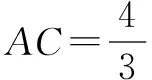
(2)因为AD∥BC,所以∠ACB=∠CAD,
又因为∠BAC=∠ADC,所以△ABC∽△DCA,
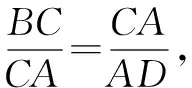
因为AD∥BC,所以∠ADB=∠CBD,
因为BD平分∠ABC,所以∠ABD=∠CBD,
所以∠ADB=∠ABD,所以AB=AD,
所以CA2=BC·AB,
所以△ABC是比例三角形;
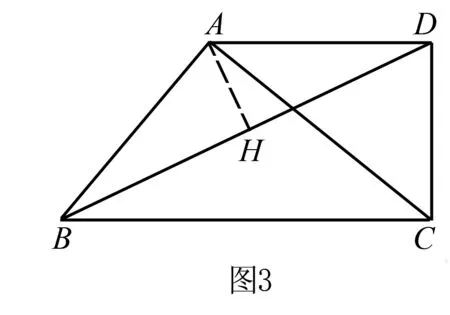
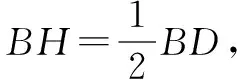
因为AD∥BC,∠ADC=90°,所以∠BCD=90°,
所以∠BHA=∠BCD=90°,
又因为∠ABH=∠DBC,所以△ABH∽△DBC,

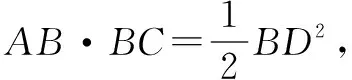
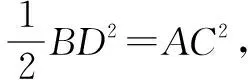
三、题型分析
此题目类型属于近些年比较流行的“新定义”型.所谓“新定义”型问题,主要是指在问题中定义了初中数学中没有学过的一些概念、新运算、新符号,要求学生读懂题意并结合已有知识、能力进行理解,根据新定义进行运算、推理、迁移的一种题型.通过该题目的三个设问来看,笔者认为,出题人的意图应该是给定“比例三角形”这样一个没有学过的一些概念,从而在学生理解概念的基础上,设置了三个问题.第一个问题意在考查“比例三角形”简单应用;第二个问题意在考查如何判定“比例三角形”;第三个问题需要结合辅助线的添加以及相似三角形的相关知识,意在考查“比例三角形”的灵活运用.
四、问题呈现
笔者所在学校的学生为电脑摇号分班,班级两极分化现象较为严重.学生们在做这道题目时,大部分同学只能完成前两个问.对于第三个问,学生做起来有一定难度.为了使题目有区分度,出题人这样设置三个问题无可厚非.但笔者发现成功做出第三问正确答案的同学,几乎都没有选择参考答案提供的方法.这引起了笔者的思考,是学生们的思维方式有问题还是第三问的设问有问题?下面将学生的做法呈现如下:
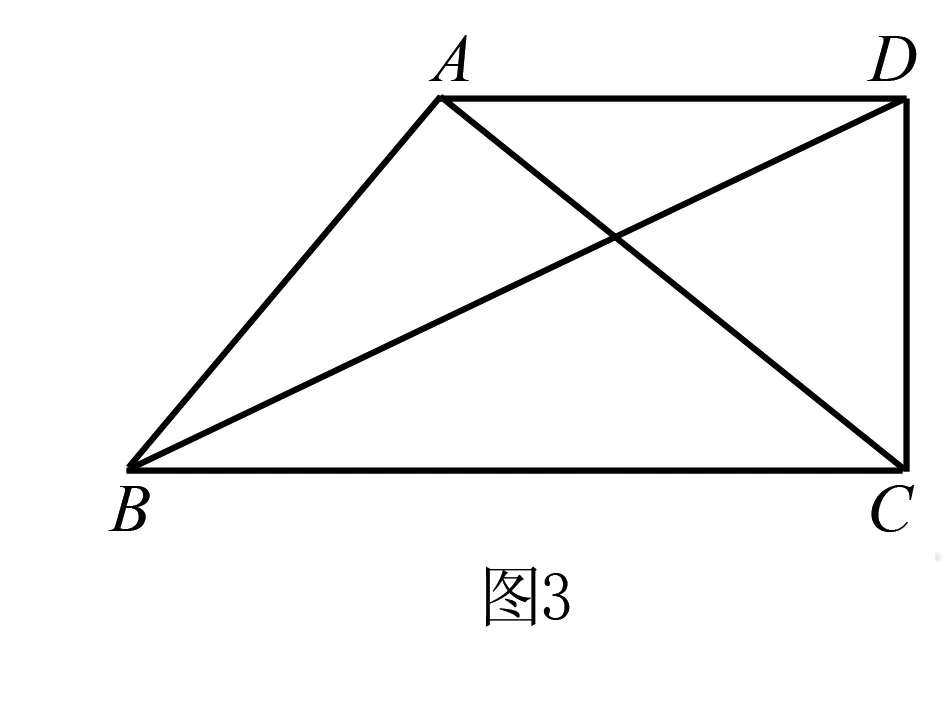
设AD=AB=a,DC=b.
在Rt△ADC中,根据勾股定理可得AC2=AD2+DC2=a2+b2;
在Rt△ABC中,根据勾股定理可得BC2=AC2+AB2=2a2+b2;
在Rt△BCD中,根据勾股定理可得BD2=BC2+CD2=2a2+2b2.
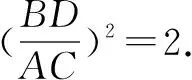
这种做法很明显比参考答案更简洁,学生也更容易理解,但问题在于如果用这样方法的话,解答过程中和“比例三角形”这个概念关系不大,甚至可以跳脱出这个题目,单独将第三问设立为一个独立问题:
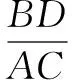
五、笔者思考
一道题目的设问,梯度上应该是由易到难,层层递进.几个设问之间也应该是相互呼应,考查方向明确而且符合学生的认知水平.基于以上考虑,笔者认为,此题第三个设问,如果改成
“(3)如图2,在(2)的条件下,当∠ADC=90°时,求的值.”是否更自然,合理一些?这样的更改的话,如果学生依然沿用“勾股定理”的解法,解答如下:
设AD=AB=a,DC=b.
在Rt△ADC中,根据勾股定理可得AC2=AD2+DC2=a2+b2;
在Rt△ABC中,根据勾股定理可得BC2=AC2+AB2=2a2+b2;
发现无法解答,进而在思维困惑下,重新回归题目,发现设AB=x,BC=y.
利用第二个设问的结论,可以得AC2=AB·BC=xy,
在Rt△ABC中,根据勾股定理可得BC2=AC2+AB2.
这样设问使得题目更连贯也更符合学生的认知,而且此题的答案是黄金分割知识中的黄金数,因而可以在此基础带领学生们进一步探究AB和BC的交点O的特殊性.第四个设问也应运而生:交点O是否为线段AB的黄金分割点?交点O是否为线段BC的黄金分割点?
笔者认为,“解题”的目的不仅是为找到正确答案,更重要的是搞清问题的来龙去脉,建立学习的整体结构,发展数学核心素养.“理解数学一理解教学一理解学生”,让学生在学习的过程中逐步达成“获得数学的基本思想’的目标,提高数学素养,发展思维能力.问题之解此中来,“问题”与“解”才更有价值.
