基于Orcaflex 的海上升压站浮吊耦合动力分析
2021-08-05邓映雪沈侃敏
梁 宁,邓映雪,李 磊,沈侃敏
(1.中国电建集团华东勘测设计研究院有限公司,浙江杭州 311122;2.浙江海洋大学船舶与海运学院,浙江舟山 316022)
海上风能是重要的清洁能源之一,近年来国内外对海上风能的开发呈井喷之势。而海上升压站是海上风电工程的核心设备,海上风机产生的电能将由该设备完成升压后通过高压海底电缆传输至陆地,因此在海上风电场的建设中,升压站上部组块安装的顺利与否对整个工程的进程有着至关重要的影响。
目前国内外海上风电多位于几米至几十米水深的近岸海域,海上升压站基础多采用导管架式结构,上部组块常利用驳船运输至作业海域进行锚泊固定,而后利用浮式起重船进行升压站上部组块浮吊安装。但由于受风浪流载荷作用,起吊前驳船是否走锚对升压站的安装至关重要,同时也是安装作业中最核心的技术难点。而目前科研人员大多关注海上升压站的安装技术以及总体布置、结构强度等问题。如王建楹等[1]以某300 MW 海上升压站为例,开展总体结构布置研究,通过对复杂海洋环境下的输电设备、平台设置以及平台结构的融合研究,提出了升压站模块化结构布置的设计思路,达到了整体布置合理可行、运维安全便捷的设计目标。毕远涛[2]对大丰H3 海上升压站的安装技术开展了详细研究,针对结构施工环节遇到的各种技术难题,参考常用措施提出了相应的解决方法,并经实际施工验证有效可行。
本文主要计算在风浪流载荷作用下,运输驳船是否会发生走锚情况。文章首先利用SESAM/HydroD 软件进行船体水动力分析,求解船体附加质量、势流阻尼、波浪力RAO 以及位移RAO 等参数,而后将水动力参数输入到Orcaflex 中开展船体-系泊的时域耦合动力分析,计算船体六自由度响应和系泊缆张力,并根据API RP 2SK 规范进行校核,为海上升压站的安装提供依据。
1 数值计算
1.1 模型参数
升压站运输采用某甲板驳由南通码头基地运输至广东某海域进行海上吊装,该船采用锚泊定位方式,作业水深30 m,由振华30 进行升压站浮吊安装。船体基本参数如表1 所示,起吊作业工况如表2 所示,船体湿表面模型和质量模型由SESAM/GeniE 建立,Panel 模型如图1 所示。

表1 甲板驳基本参数Tab.1 Basic parameters of covered barg

表2 起吊作业工况Tab.2 Working condition of hoisting

图1 甲板驳panel 模型Fig.1 Panel model
1.2 环境工况
考虑到浮吊安装方便,驳船锚泊方案如图2 所示。此时浮吊船正对于驳船船宽方向,升压站上部组块起吊后立即撤掉驳船,浮吊船沿船长方向移至导管架结构即可安装。计算环境条件参考作业海域海洋水文资料,具体计算海况如表3 所示。其中船体系泊的耦合动力分析在Orcaflex 中进行,计算中流力系数和风力系数参考OCIMF 发表的超大型油船风载和流载计算方法[3]。
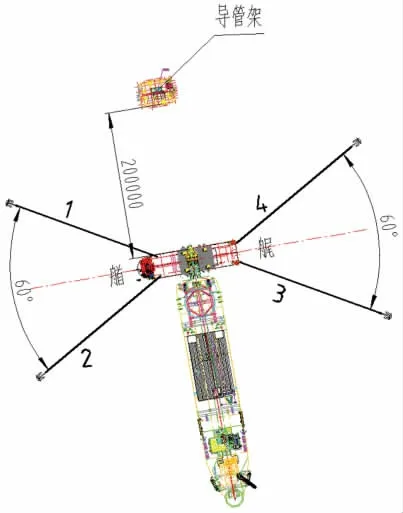
图2 锚泊布置情况Fig.2 The arrangements of mooring

表3 作业海况Tab.3 Sea conditions
根据海洋水文资料中实际载荷作用方向,取浪向为125°和147.5°,流向为156°和198°,风向为192.7°,计算载荷组合工况如表4 所示。

表4 计算工况Tab.4 Computational conditions
1.3 限制条件
驳船工作锚缆选取依据GB/T33364-2016 海洋工程系泊用钢丝绳,系泊缆属性如表5 所示。

表5 锚缆属性Tab.5 Properties of anchor cable
锚缆安全系数参考API RP 2SK 规范[4],短时期锚泊计算下,完整工况锚索的安全系数取2,锚的安全系数为1。本设计中锚的规格为7 t,锚抓力系数为12,因此最大抓力为84 t,因此锚缆张力应小于84 t(最大抓力84 t 乘以安全系数1),否则会出现走锚问题[5]。
2 计算结果
船体锚泊的耦合动力分析基于Orcaflex 软件计算求解,计算中缆绳预张力约10 t,其中波谱类型选取JONSWAP 谱,并考虑风、浪、流环境力综合作用进行锚泊状态下的运动时域分析,得到锚缆的受力时历曲线,最后按照3 h 回归周期[6-7]获得锚缆的最大张力和船体运行响应。
如图3 所示,船体3 个平移运动自由度(横荡、纵荡及垂荡)的幅值响应算子远大于旋转运动3 个自由度(横摇、纵摇及首摇)的幅值响应算子,因此可论证船体的平面运动响应为铺管过程的限制条件。

图3 船体运动幅值响应算子(RAO)Fig.3 RAOs of ship motion
纵荡对波浪比较敏感的频率区间小于0.8 rad·s-1,迎浪和随浪工况对纵荡影响最大,横浪向影响几乎为零;横荡对波浪比较敏感的频率区间小于1.2 rad·s-1,横浪工况对横荡影响最大,而迎浪和随浪向影响几乎为零;对于首摇运动,迎浪、随浪和横浪向频响函数始终为零,而艏斜浪和尾随浪方向响应的敏感频率区间为0.3~1 rad·s-1,峰值出现在0.6 rad·s-1。
表6 所示为锚泊计算所得各工况下锚缆的最大张力。对比工况LC1 和LC2 或LC3 和LC4 数据可知,锚缆最大张力与海流力作用方向基本一致(LC1 和LC3 流力方向为156°,与锚缆#3 布置方向基本相同;LC2 和LC4 流力方向为198°,与锚缆#4 布置方向基本相同)。因此本计算中流致拖曳力是锚缆张力的控制因素,同样的结论也可以对比LC1 和LC3 或者LC2 和LC4 数据可得,改变波浪入射方向对最大受力锚缆无影响[8]。

表6 各工况锚缆最大动态张力Tab.6 Maximum dynamic tension of anchor cable with various conditions
由表6 可知,风浪流载荷作用下各工况各锚缆最大张力为45 t,出现在125°波浪、156°海流以及192.7°风载作用时,此时#3 受力最大。此时最大锚缆受力载荷小于缆绳破断拉力173 t,因此缆绳可以正常工作。而此时根据API RP 2SK 规范要求,本设计选取的锚的最大抓力为7×12×1=84 t,锚缆张力远小于锚的最大抓力,因此该甲板驳锚泊状态下不会出现走锚问题。
图4 所示为各工况下最大张力锚缆的时域动态张力曲线。图示可知,锚缆最大张力均为瞬态最大张力,最大张力为一个或若干峰值,张力大小在某一平衡位置上下循环往复振荡,这与船体的大幅值平面运动相符[9]。同时由图4 和表6 可知,LC1 和LC3 时的锚缆张力比LC2 和LC4 要大。结合表6 结论可知流致拖曳力是本锚泊作业的主控环境条件,而波流同向时能大大增加锚缆的受力,因此实际作业时的风浪流是否一致是施工作业人员要特别注意的额外条件。
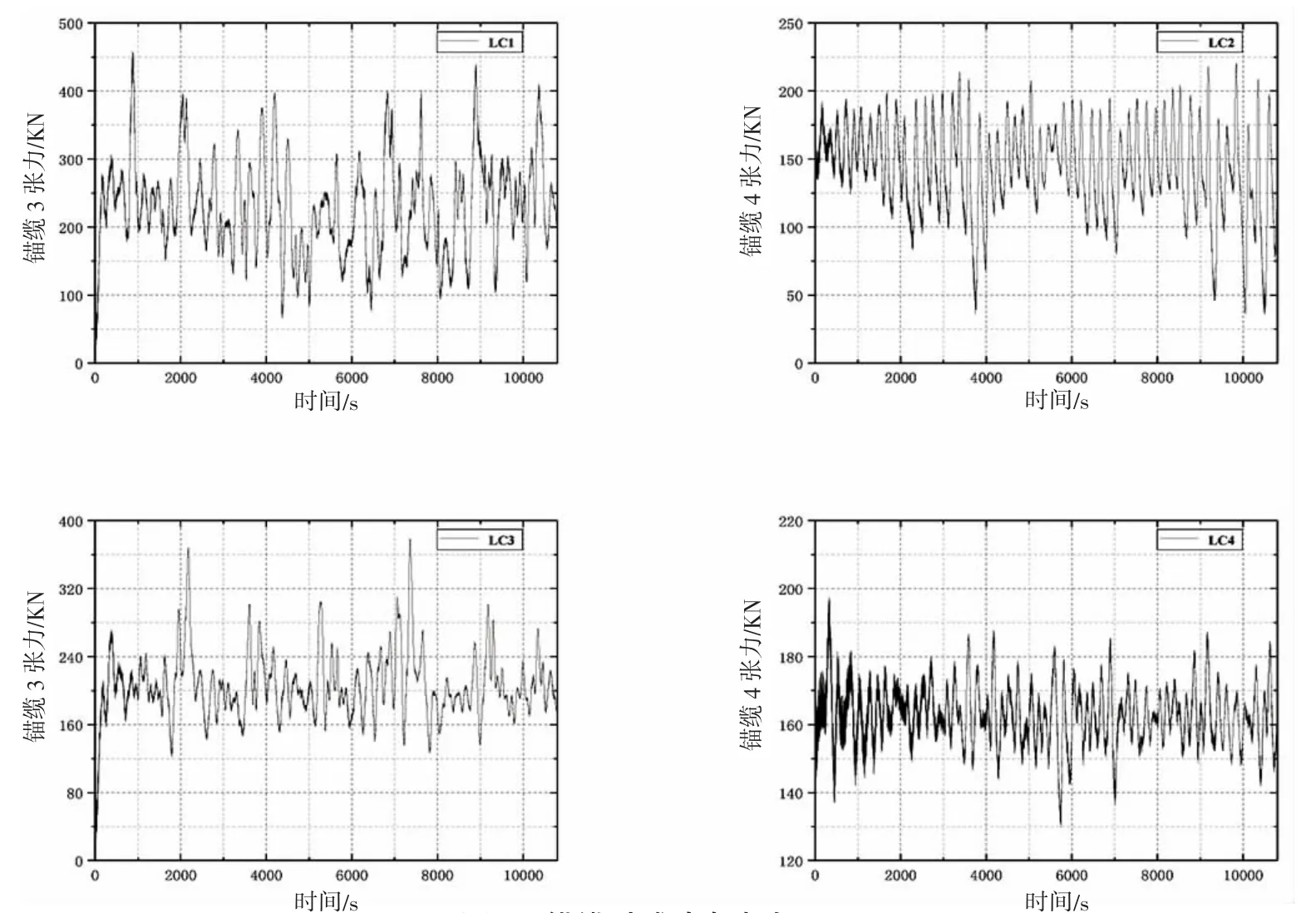
图4 锚缆时域动态张力Fig.4 Time domain dynamic tension of anchor cable
3 结论
针对阳西海上升压站运输起吊过程中的走锚问题,本文基于当地水文观测资料,建立合理的起吊数值模型,通过开展浮体——锚泊系统的耦合动力计算,得到船体六自由度运动响应和锚缆时域动态张力,计算获得如下重要结论:
(1)各工况中锚缆最大张力大小随环境条件变化。由计算结果可知,缆绳张力随流向和浪向的改变而变化,当流向和浪向相一致时缆绳张力较大,且最大张力亦在该工况;当流向和浪向相反时会降低锚缆张力,出现受力抵消现象,因此实际施工中应注意风浪流同向问题。
(2)本设计中的缆绳和锚的型号满足作业要求。根据计算结果可知,各工况下最大锚缆张力45 t,出现在LC1 中的3 号锚缆,而此时最大张力小于锚缆最小破断张力和锚的最大抓力,因此满足要求,不会出现走锚问题。
