基于改进粒子群优化算法的船舶航向控制

樊灵美，陈 林，王恒家，王化明

(1.浙江海洋大学船舶与海运学院，浙江舟山 316022；2.浙江海洋大学东海科学技术学院，浙江舟山 316000)

通过整定PID 控制器的3 个参数实现控制系统收敛速度快、超调量小和鲁棒性能强等优势。虽然PID控制器有3 个控制参数可以调整，但找到一组合适的PID 参数仍然不是一件非常简单的事情。早期提出的整定方法一般是在离线的情况下整定，不能及时地在线调整参数。

自动舵是渔业船舶控制系统中一个不可缺少的重要设备，随着对航行安全及营运需求的增长，人们对自动舵的要求也日益提高。由于渔业船舶运动的复杂性，渔业船舶动态特性具有大惯性、大时滞、非线性，受到的环境影响是随机和难以预测的，并且传统的自适应控制等控制方法无法有效控制未建模动态系统，从而影响了传统舵和自适应舵的控制效果。为了解决上述问题，需要进一步将智能控制技术引入到自动舵控制技术中，研究混合型的智能自动舵，PID 与遗传算法结合以及PID 与粒子群算法结合等，以适应渔业船舶航向控制的高要求。

大自然与科学技术相辅相成，大自然的生物特性和演化过程带给科学家们很大的灵感，所以利用各种优化方法来解决PID 参数优化问题应运而生。例如N.Metropolis 教授观察固体内部粒子随温度的升高变为无序状的现象相似于一般组合优化问题而提出的模拟退火算法[2]，模仿自然免疫系统功能的一种智能方法人工免疫系统依据鸟群寻找栖息地的活动规律提出的PSO 算法等。总而言之，结合生物智能优化思想进行优化是解决粒子退化问题的主要方法之一，一般利用模拟退火算法、模糊控制算法、改进人工免疫算法和PSO 优化算法等以及这些算法的混合来优化PID 控制参数[3]。

PSO 优化算法就是把船舶航向控制过程中每一个运动状态变量看成没有大小和重量的粒子，模拟群体中个体和群体之间相互协作与竞争，利用信息共享的模式，使得个体与群体都向着好的方向发展。以一定的速度来决定方向和距离，此运动速度的动态调整主要依据于个体的运动经验和群体的运动经验[4]。因此，PSO 优化算法对船舶运动状态的真实变量有积极的作用。

考虑到粒子群迭代次数和搜索过程中目标函数对PID 参数值有一定的影响，因此主要研究改变迭代次数和目标函数来比较对应的PID 参数，根据不同PID 参数对应不同的控制效果，实现控制系统最优化的效果。

1 船舶航向控制数学模型

1.1 船舶响应型数学模型

因为船舶自身体积庞大、外形复杂多样且实验的成本非常大，继而不能在理论水平上准确计算出船舶的流体力导数，所以需依靠船舶运动数学模型实验来计算船舶流体力导数。船舶航向控制数学模型一般有响应型数学模型和水动力数学模型，其中水动力数学模型分为只在静水面操纵的分离型数学模型和用整体的观点来计算船体的流体动力的整体型数学模型。由于水动力数学模型的参数过多，而且大部分参数值用回归公式或经验公式才能计算出，导致大多数船舶模型的参数值存在误差。响应型数学模型只需要2 个参数且可以在运行过程中动态调整参数，所以采用船舶响应型数学模型作为实验模型[5]。一阶响应型数学模型(野本谦作的Nomoto 模型)和二阶响应型数学模型是响应型数学模型的两大分支，Nomoto 模型具有动态调整的特性，在船舶航行控制的过程中根据舵角发生的变化及时调整控制规律，使船舶能够准确航行到预定航向。

公式(1)是Nomoto 模型的船舶运动方程式：

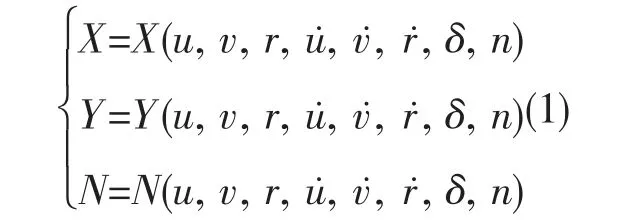
上式中，u,v,r 是船舶平面运动的基本变量，u,v 表示移动速度，r 代表转动角速度，它们的时间导数分别用表示；舵角用来δ 表示；螺旋桨转速为n；流体动力X、Y 和力矩N 是它们的非线性函数[3]。

一般来说流体动力导数采用无量纲的形式便于准确数据处理。下面是一些基本的度量单位：

长度L0-L(船长)

速度V0-V(航速)

时间t0-L/V

质量m0-(1/2)ρL3

力F0-(1/2)ρV2L2

力矩M0-(1/2)ρV2L3

其中ρ 是水密度。

使用野本谦作的Nomoto 模型进行船舶运动控制仿真实验有2 大优势：

(1) 模型简单，各项表示的参数可从模型实验中直接得到，计算方便。

(2) 处于低频范围时，低频频谱和高频频谱十分接近。

下面是Nomoto 模型需要船舶参数：航速V，船宽B，两注间长L，满载吃水T，Cb代表方形系数，重心距中心距离表示Xc，排水量为Δ，Aδ代表舵叶面积。

采用如下公式(2)“育龙”轮数学模型的传递函数：

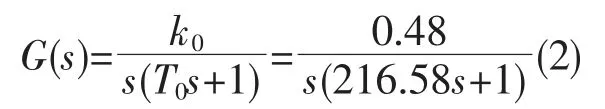
其中，T0为时间常数，k0为常数。

1.2 舵机伺服系统数学模型

舵机作为船舶控制航向的核心设备，能够保障船舶在海上安全稳定航行，船舶在海上的航行位置及方向主要依靠于舵机伺服系统。船舶舵机伺服系统是船舶的执行机构，主要由一个伺服机构来驱动[6]。舵机可分为气动式、液压式和电动式。电动式舵机凭借质量小，结构简单，体积小和成本低的优点而被广泛认识及运用。一般来说，舵机数学模型可以表示为如下公式(3)的一阶惯性环节[7]：

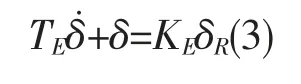
其中，TE为舵机时间常数，一般取2.5 s为舵角的时间导数；δ为舵角；KE为舵机控制增益，一般为1；δR为控制舵角。

1.3 海浪干扰模型

海浪的干扰是船舶在海上航向控制的主要干扰之一，主要包括高频波浪干扰力和波浪漂移力，它用一种简单的白噪声驱动的传递函数来模拟，如下公式(4)的二阶振荡环节传递函数[3]：

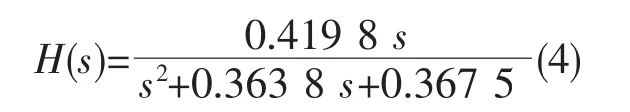
其中取白噪声能量为10，采样周期为1 s。波浪干扰力分为一阶干扰力和二阶干扰力。传递函数输出一种相当于6 级风作用下的海浪干扰化角，船舶相当于一个低通滤波器，直接模拟在船舶模型上使船舶运动航向控制模型得到的值更加准确[8]。

研究表明：在PSO 全局寻优的基础上分别控制无波浪条件下船舶航向控制和有波浪条件下船舶航向控制，比较得出在有波浪的条件下得出的曲线更接近于船舶运动的真实状态的值[9]。

1.4 PID 控制器

船舶航向控制在船舶运动的前提，在船舶航向控制中，船舶操纵占据了船舶航向控制的重要地位，然而传统的操纵方式已经无法保障当今船舶航行的安全性和经济性，所以把船舶的操纵性能提升的任务迫在眉睫。船舶安装自动舵帮助船舶操纵性能的提高，自适应PID 舵随着伺服机构原理发展起来[10]。

早期控制领域提出的PID 反馈控制器现在仍然处于控制的主要地位。因为PID 控制技术不需要被控对象的精确数学模型，只需要对象的响应特性就能控制，所以它广泛使用于船舶控制领域。计算机控制首先采样各时刻的输出与输入的偏差值，然后来计算控制量，而且采样后的PID 控制算法的值需要离散化后才能使用，最后把得到的控制量运用到控制对象中。其控制理论非常简单：利用偏差来消除偏差，属于线性控制策略中的一种控制。

常规PID 控制算法主要解决线性的控制系统，但在真实情况下船舶运行工况往往发生变化。从理论层面来说，船舶一般处于非线性运动状态下，一般是来源于两个方面：船舶纵向速度的变化和流体力导数的非线性存在。性能佳和整定优良是当今常规PID 控制器参数不具备的特性，所以常规PID 控制器容易造成超调量较大、调节时间较长和系统的控制品质不佳，而且它不具备在线调整参数的功能，限制了控制效果，所以在此基础上设计出了非线性的PID 控制，然后得出非线性控制参数的值，再加入粒子群寻优。

图1 为常规PID 控制的原理框图。

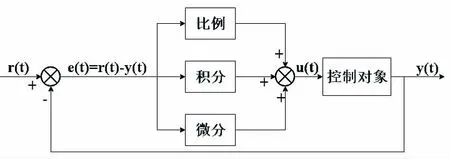
图1 常规PID 控制的原理框图Fig.1 General PID control principle block diagram

2 PSO-PF 算法原理

常规的PID 控制算法对于非线性和多峰值复杂函数的优化问题无法处理，但是粒子滤波方法可以解决这些问题。原因是它的原理比较容易、需要调节的参数较少和控制效果明显，再加上它不受限于控制系统模型特性与噪声分布。粒子滤波目标就是在有干扰的观测信号中大约推断出所需状态信号值，即随着时间演变不断测量系统观测信号，在一定滤波准则的基础上，来达到系统状态的最优化估计，所以考虑将这种粒子滤波方法用于船舶航向控制上，让船舶航向控制更加准确。

粒子滤波主要应用在跟踪和定位这两个领域，船舶航向控制就是利用这两个特性。但是粒子滤波的粒子退化问题是我们在船舶航行控制中不容忽视的问题，随着迭代次数的增加，粒子多样性就开始减少。为了解决粒子退化的问题，我们一般可以采用以下一些方法：重采样方法，裂变自举粒子滤波，高斯滤波与粒子滤波相结合以及基于智能优化算法的粒子滤波[11]。

基于智能优化的粒子滤波主要是保留那些好的粒子，使其他粒子能向好的粒子域分布，以至于增加了粒子分布的多样性，也能使最后得到的适应值比较准确。粒子群优化算法(PSO)是一种模拟群体中个体和群体之间相互协作与竞争的粒子滤波，利用信息共享的模式，使得个体与群体都向着好的方向发展，增强系统的抗干扰能力且系统无超调。

鸟类寻找栖息地与船舶行驶到预定位置的方式很相似。PSO 算法起源于他们观察到鸟类这样的群体行为，然后进行建模与仿真，PSO 算法不但保留了对个体的进化算法还拥有了基于群体的全局搜索方法。PSO算法基于“群体”和“进化”且优化过程依据粒子适应值的大小[4]。

粒子飞行速度和位置以公式(5)(6)来调整：

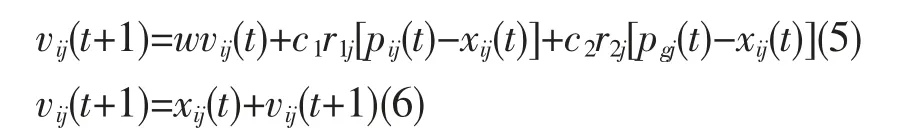
其中下标i 表示粒子i，j 表示粒子所在的位置是第j 维；t 代表第t 代；c1，c2为取值在0～2 间的加速常数，c1和c2分别表示为调节粒子飞向个体和全局最优位置方向的步长，数值越大算法收敛速度越快；w 代表惯性权重，w 在粒子寻优的范围内不是一个固定的值，它的范围一般取0～1，初始时一般取值稍大一些，利于获得全局范围内最优解，而在后期一般取稍小一点的值，有利于在局部区域内获得更好的最优解；r1～U(0,1)，r2～U(0,1)是2 个取值均匀的相互独立的随机函数；上式vij∊[-vmax,vmax]目的是不允许粒子离开n 维搜索空间。PSO 算法具体方法如下：首先设置所有粒子数目用字母m 表示，第i 个粒子位置为Xi=(xi1,xi2,…,xin)，速度为Vi=(vi1,vi2,…,vin)。每一次迭代粒子的速度和位置的变化通过2 个极值进行不断地更新，其中一个极值是个体最佳适应值Pi=(pi1,pi2,…,pin)；另一个是粒子种群目前所在位置的最优解的全局最佳适应值，一般可以表示为G=(g1,g2,…,gn)。在优化结束之前，粒子本身的位置和速度不是固定的，需要不断地更新自己的速度和位置[12]：

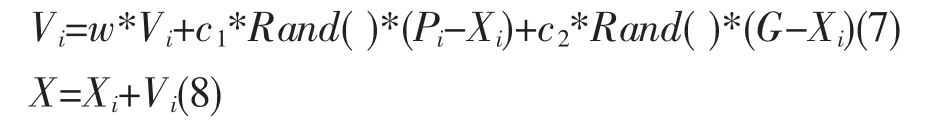
上式中，Rand 是随机数，一般取0～1；c1和c2统称为学习因子，一般情况下学习因子c1=c2=2。w 是惯性系数。

3 目标函数

达到目标函数的时间长短是衡量系统控制性能强弱的指标，不同的目标函数有属于自己的最佳优化值。在船舶航向的控制系统中，出现设定航向与实际航向偏差较大时，通过施加一定的舵角可以减小航向的偏差，但与此同时增加了船舶航行时的阻力及船速损失变大。因此，需要将舵角和航向偏差都考虑在内。故而在公式(9)(10)(11)中寻求最佳的目标函数来最快的达到预期控制效果[3]。

其中航向偏差e 为控制器输入；w1为权值0.1。该目标函数只考虑了航向偏差，增加了船舶航行时的阻力及船速损失变大，未考虑到舵角的影响因素。

为了达到快速、经济、安全航行的目的，船舶航向的偏差应尽可能小，舵角的变化应尽量小，由此采取下列公式(10)：

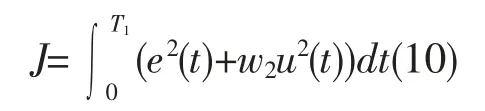
上式(10)中，其中航向偏差e 作为控制器输入；w2为加权系数，w2取值为0.1；u 为控制器输出。

考虑到航向角误差会影响到航向精确度，所以采用航向角误差时间积分性能指标，目的是获得更高的航向控制精度[6]，并且对控制器输入也加入加权系数。采取下列公式(11)的二次型性能指标：

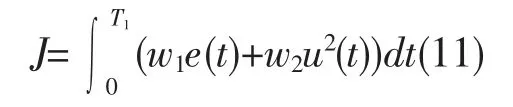
上式(11)中，w1，w2都为0.1 的加权系数值。w1e(t)表示航向角误差的时间积分性能指标；w2u2(t)表示航向角实际输出的平方时间积分性能指标，目的是防止航向角输出过大，降低了工作强度，使得船舶航平缓地趋近期望值。目标函数是粒子群优化算法必不可或缺的一个部分。

4 约束条件

航向保持时，希望航向偏差尽量小，舵角变化不要太频繁，同时要求转首角速度小于某个上限。约束条件描述为：

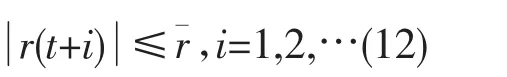
航迹保持时，除了希望航迹和航向偏差小、舵角变化不要太频繁、转首角速度满足(12)外，还要求满足航向偏差在某个范围内：

其中，Ψs为设定舵角。

5 仿真实验与分析

为了验证上述PID 航向控制器对船舶航向的控制是否有良好的效果，通过MATLAB 做仿真实验。设置加速常数c1=c2=2；粒子规模数20；惯性权重的取值wmin=0.4，wmax=0.9；粒子在n 维搜索空间中最小位置是[0，0，0]与最大位置是[10，0.1，100]；粒子飞行速度取值范围[-1,1]；最小适应度为0.1；迭代次数取100次；w1和w2取0.1。采用“育龙”轮Nomoto 模型：航速为15 kn、船宽为20.8 m、两注间长为126 m、满载吃水为8 m、方形系数0.681、重心距中心距离0.25 m、排水量14 278.12 m3、舵叶面积18.8 m2。输入舵角为5 的阶跃响应，在数学模型中设置人工整定常规比例系数Kp=3，积分系数Ki=0.002，微分系数Kd=40。目标函数采用公式(11)来进行仿真，参数值如表1 所示。

表1 船舶模型参数Tab.1 Parameters of ship model

下图由MATLAB 仿真船舶航向控制得出的曲线。船舶航向控制由船舶响应型数学模型、舵机伺服系统、海浪干扰模型和PID 控制器构成，再加上粒子群寻优算法(PSO)。该船舶运动数学模型能够快速稳定得出3 个参数的最佳适应值。通过sinmulink 仿真得出图2、图3、图4 和图5：

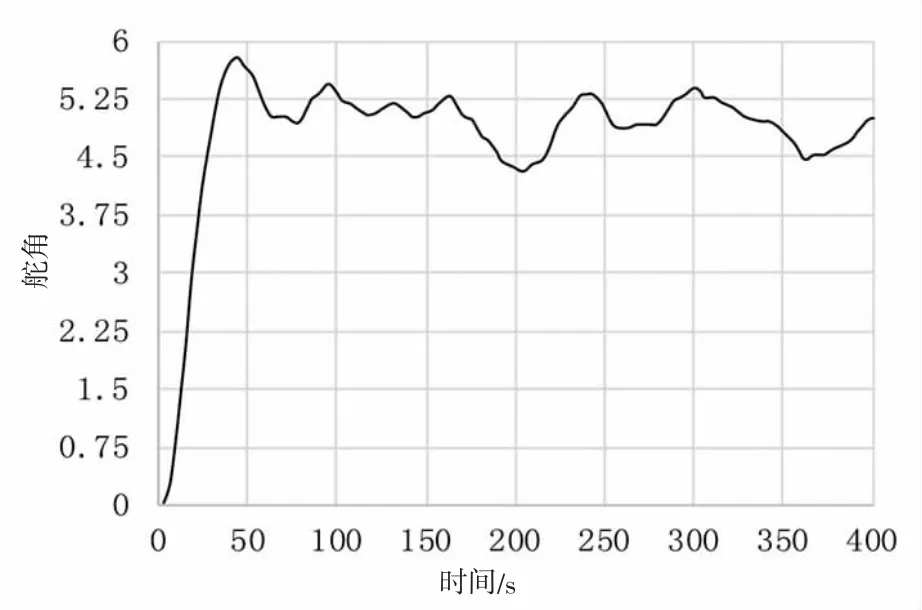
图2 航向阶跃响应曲线Fig.2 Course step response curve

图3 舵角输出曲线Fig.3 Rudder angle output curve

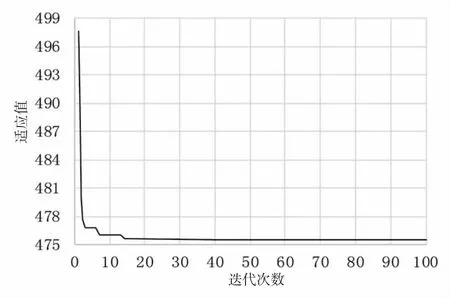
图4 最优个体适应值Fig.4 Optimal individual fitness value

图5 Kp、Ki 和Kd 优化曲线Fig.5 Kp,Ki and Kd optimize the curve

观察上列图形可得出，图2 航向阶跃响应出现了超调，输入舵角是5，航行阶跃曲线峰值几乎达到了6，超调量较大，而且收敛所需的时间长。图3 中的舵角输出曲线在白噪声的干扰下，曲线波动较大。图4最优个体适应值在迭代次数20 时就可达到全局最佳适应值475.541 5。图5 可以得出全局寻优后的参数：比例系数Kp=3.093 1，积分系数Ki=0，微分系数Kd=59.169。

猜想迭代次数的大小是否影响PID 的参数的值。用表2 来比较不同的迭代次数而得到相应的全局最佳适应值和PID 的参数。

由表2 可知，Bestf 为个体最优适应值；Fzbest 为全局最佳适应值。迭代次数在90 之后，3 个参数值达到稳定值。根据表2 的数据分析比较，可得出图6、图7 和图8。

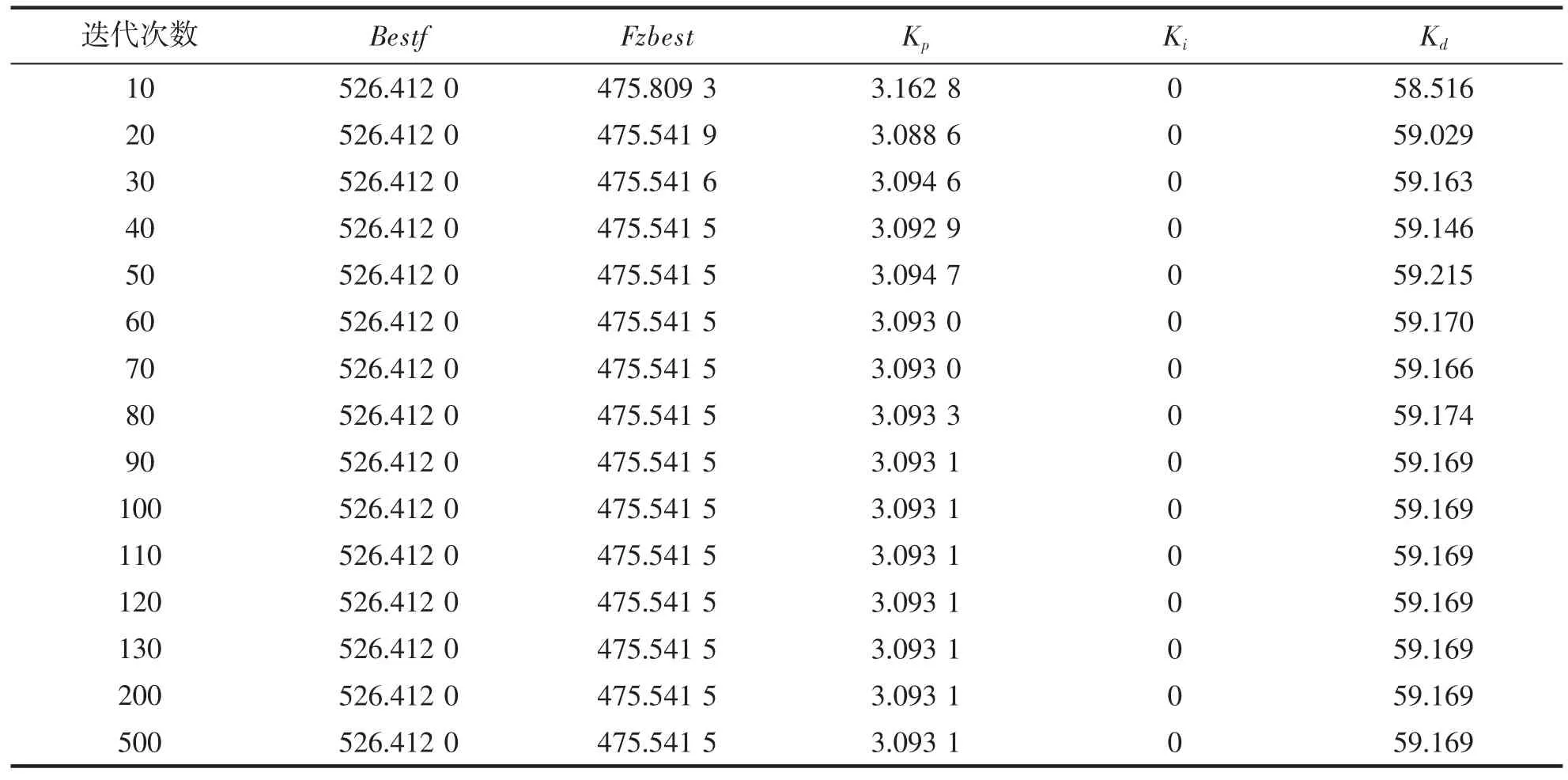
表2 迭代次数对应的PID 参数Tab.2 The PID parameter corresponding to the number of iterations

由图6、图7 和图8 可知，PID 3 个控制参数比例系数Kp，积分系数Ki和微分系数Kd变化范围很小，并且在迭代次数90 之前，比例系数Kp与迭代次数成反比关系，积分系数Ki几乎保持不变，微分系数Kd与迭代次数成正比关系。迭代次数到达90 时，比例系数Kp=3.093 1、积分系数Ki=0.00 和微分系数Kd=59.169 0 这3 个参数值几乎都到达稳定值，在迭代次数90 后的PID 参数几乎没有发生变化。

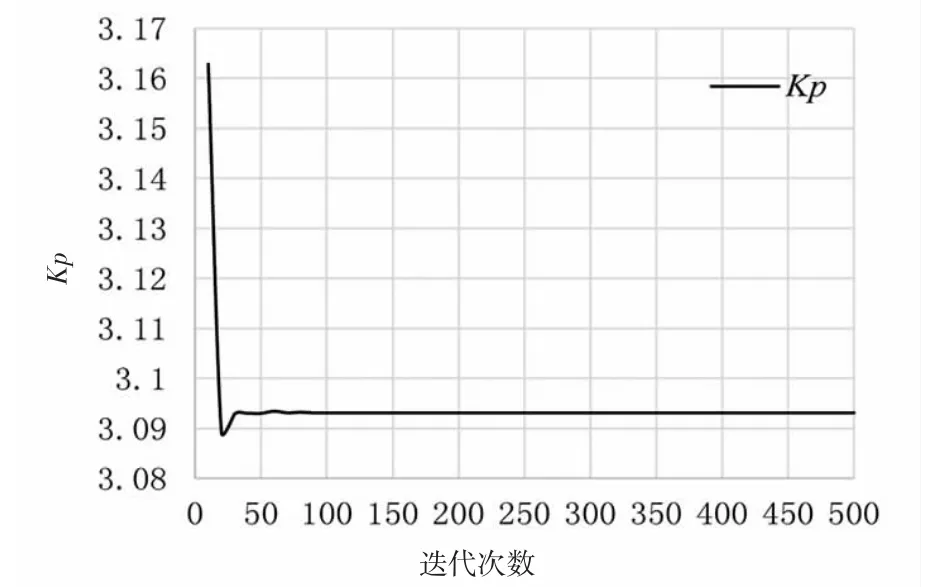
图6 Kp 随迭代次数变化的曲线Fig.6 The curve of Kp changing with the number of iterations

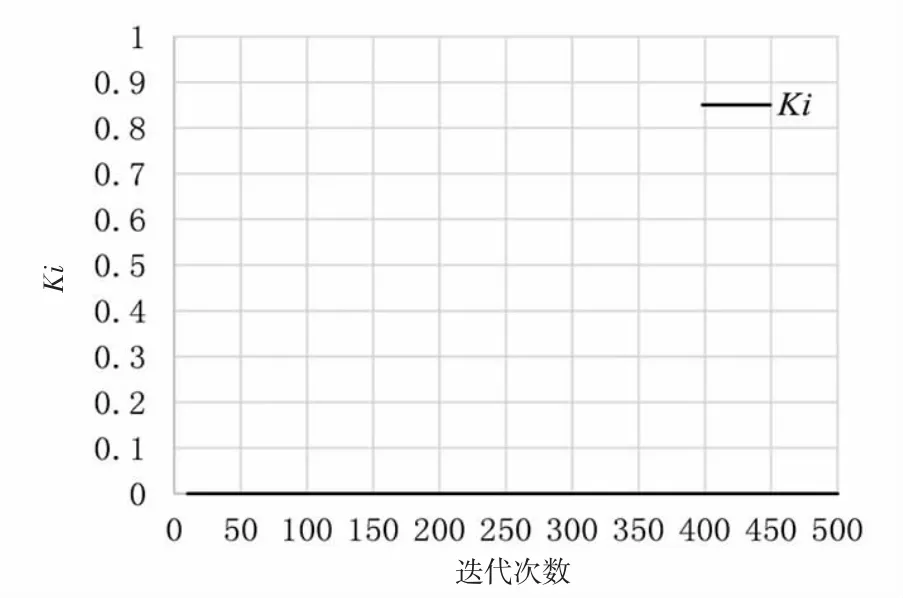
图7 Ki 随迭代次数变化的曲线Fig.7 The curve of Ki changing with the number of iterations

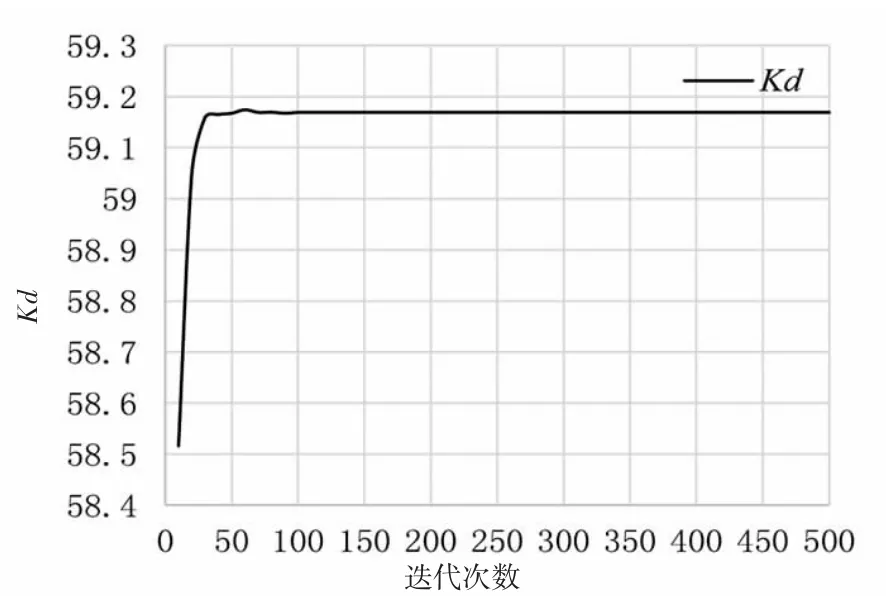
图8 Kd 随迭代次数变化的曲线Fig.8 The curve of Kd changing with the number of iterations

迭代次数90 时候能够更快更准确地到达输入的舵角。为了节约时间来快速达到最优控制参数，可以选用迭代次数为90 的PID 控制常规参数Kp=3.093 1，Ki=0，Kd=59.169 来比较之前的航向阶跃响应(对比图2)。

图9 分别为人工整定和改进PSO 的控制参数得出的航向阶跃响应曲线。图9 中明显可以得出，当迭代次数达到90 次时，经过改进粒子寻优算法(PSO)得到的比例系数Kp=3.093 1，积分系数Ki=0，微分系数Kd=59.169 的值和常规的参数值比例系数Kp=3，积分系数Ki=0.002,微分系数Kd=40 对船舶进行航向控制比较，改进粒子寻优算法(PSO)更快地达到初始航向舵角5，而且比较稳定，未出现超调，人工整定得出的曲线超调量十分大。并且在之后的航行中，改进粒子寻优算法(PSO)航向偏差范围比人工整定的曲线波动范围小，更快的达到收敛。所以得出结论：当迭代次数在90 的时候更稳定，未出现超调，迭代次数设为90 次时为航向控制效果最佳。

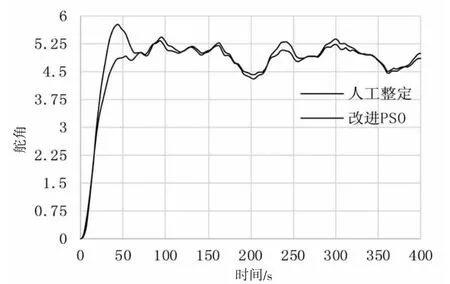
图9 航向阶跃响应(最优迭代次数=90)Fig.9 Heading step response(optimal number of iterations=90)

虽然最佳的迭代次数已经得出：当迭代次数为90 时，得到最优的航向控制效果。不同的目标函数有属于自己的最佳答案，由此观察目标函数的改变，参数的大小是否发生改变。表3 是更换不同目标函数而得出的不同的PID 参数的值：

表3 不同目标函数的比较Tab.3 Comparison of different objective functions

其中w1=w2=0.1。从表格中的数据可发现，目标函数改变，PID 的控制参数发生变化。所以得出结论：PID 控制参数受目标函数的影响，对于不同的目标函数，PID 控制参数值变化较大，全局最佳适应值的变化也较大。

6 结论

基于Nomoto 型船舶运动模型，运用舵机伺服系统、海浪干扰模型和PID 控制器来设计航向控制，并且在该航向控制中加入全局寻优算法(PSO)，建立三自由度船舶扰动模型。研究不同的迭代次数对航向控制的具体影响，观察航向控制参数的变化。发现迭代次数90 之前，Kp随着迭代次数的增加而减小，成反比关系；Ki几乎保持不变；Kd随着迭代次数的增加而增加，成正比关系。到达90 时，Kp、Ki、Kd到达稳定值。迭代次数90 时候能够更快更准确地到达输入的舵角。最佳迭代次数在90 时，能够较好的控制船舶的航向。根据目标函数的改变但PID 参数发生变化可以得出结论：PID 控制参数受目标函数的影响，不同的目标函数PID 控制参数不同，全局最佳适应值也不同。