线性插值在分配飞机整流罩气动载荷中的应用

刘 伟

（中航西安飞机工业集团股份有限公司，陕西 西安 710089）

0 引言

飞机上的整流罩常由面板和骨架组成，主要是对内部的各个设备起包络、气动维形的作用，不参与全机受力，属于次承力结构，在对结构强度进行设计时，主要考虑气动载荷的分布，惯性载荷可以忽略不计[1-3]。现成的针对如何将理论计算或风洞测压试验的气动载荷施加到有限元模型上的商业软件较少且通用性不好，一般都是通过编程对气动数据进行后置处理或对CAE软件进行二次开发，目前常用的方法是选取与设计工与工况似的气动载荷，将分布气动载荷积分转换为节点力，再遵循静力等效原则，采用三点排或多点排方法转换到有限元节点上[4-5]。

该文根据飞机的运动参数，筛选出整流罩的设计工况[6]，采用线性插值方法将各压力点的气动数据精确插值到设计工况，将每个气动网格离散为多个网格，形成密网格；按照分布等效原则，将气动载荷直接等效到有限元模型上，省略分布力转换为节点力的中间过程，解决了通用性问题，提高了工作效率。

1 计算方法

为了获取精确的整流罩气动载荷，将整流罩视为外挂物，按照规范求解飞机在不同高度、速度以及受载情况下带外挂物时全机的运动参数，并对其进行插值计算，得到整流罩的总气动载荷，筛选出整流罩严重载荷情况作为设计工况，依据压力分布数值计算数据或风洞测压试验数据，采用线性插值方法将各压力数据插值到设计工况，形成密气动网格，再转换到有限元模型上。

1.1 计算假设

为了尽可能精确地得到有限元模型上的气动分布载荷，计算需要基于以下3个假设：1）相邻节点的压力系数线性分布。2）气动外形与有限元模型一致。3）气动外形光滑、无突变。

压力系数线性分布是插值计算的基础，气动外形光滑、无突变以及与有限元模型一致是保证精度的前提。

1.2 设计工况选取

选取整流罩的严重载荷情况时，一般会忽略惯性载荷，只考虑气动载荷，应该考虑以下2个方面：1）3个方向合力及矩的极值。2）组合力及矩的极值。

以上2个方面共包括28个严重载荷情况，在实际工程中，考虑到整流罩的实际承载情况，大多数严重工况的载荷是可以忽略不计的。

1.3 设计工况插值

整流罩压力分布数据一般是通过计算压力分布数值或通过风洞测压试验获得的，不同的计算软件、风洞得到的数据格式不一致。常见的格式见表1和表2。

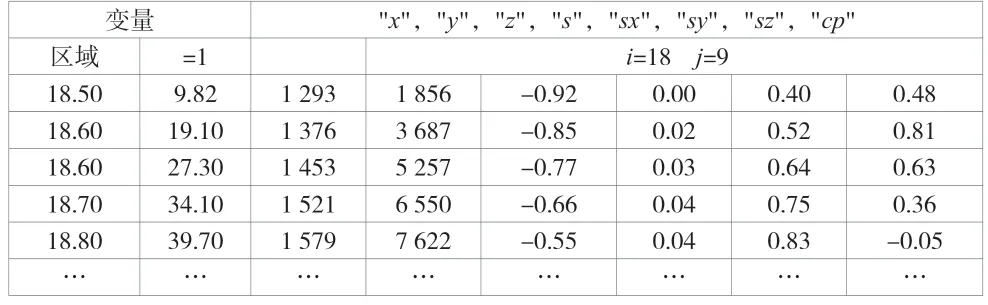
表1 压力分布数值计算结果

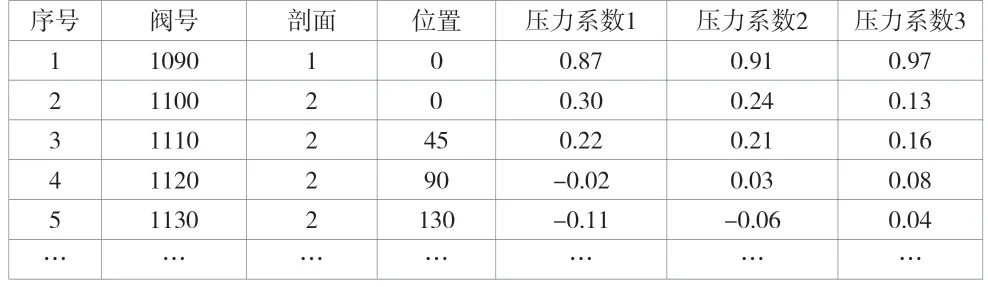
表2 风洞测压试验结果

表1和表2只是一些典型的数据格式，为了便于数据管理，对数据进行插值计算，统一气动数据的格式，每个压力点按照侧滑角、攻角、马赫数以及舵面偏角等组成数据矩阵并进行线性插值，得到整流罩在设计工况下的压力分布，各压力点的典型数据矩阵见表3。

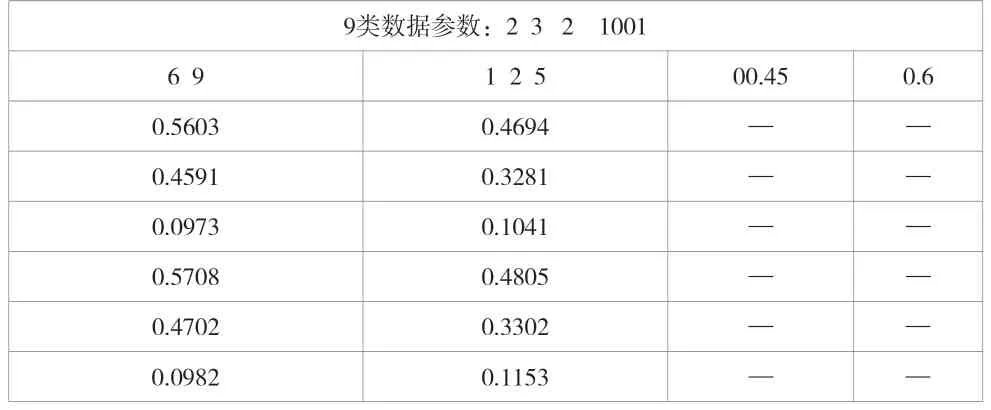
表3 压力点典型数据矩阵

表3中，“9类数据参数：2 3 2 1001”代表ID为1001的压力点由2个侧滑角、3个攻角以及2个马赫数组成数据类型为9的数据矩阵；“6 9”为侧滑角；“1 2 5”为攻角；“0.45 0.6”为马赫数；其余数据为压力系数。

1.4 离散气动数据

压力分布数值计算（CFD）得到的数据是以网格为基准而给出的，可以根据前期的划分将CFD分为若干数据块（包括I行×J列个数据点），代表不同的飞机部件或部件的一部分，每个数据块可分为I个小块，代表I行；每个小块都包括J行数据，代表J列（如图1所示），图1呈现了上面描述的CFD数据的特点。每行数据包括网格坐标、网格面积以及网格3个方向的法向量和压力系数。CFD数据自身的特点为该文的插值方法提供了数据基础。气动数据离散的基础是每个数据块可以严格的按I行J列进行数据排列，每行数据都包括满足计算要求的数据。将每个气动网格离散为多个网格，分为行的离散和列的离散，就是将每一行（列）相邻的2个点看作一组数据的起点和终点，按照空间距离进行线性插值，得到一组全新的数据，如图1所示。

图1 气动网格离散示意图

Jn代表数据块中J列第n个压力点，In代表数据块中I行第n个压力点，k1代表在每一行（列）相邻的2个点之间的空间直线上等距离增加k1个点，以k表示k1个点中任意一个点，即k＝1，2，3，....，k1，如图1所示，每个增加点对应的数值信息的计算方法如公式（1）～公式（8）所示。

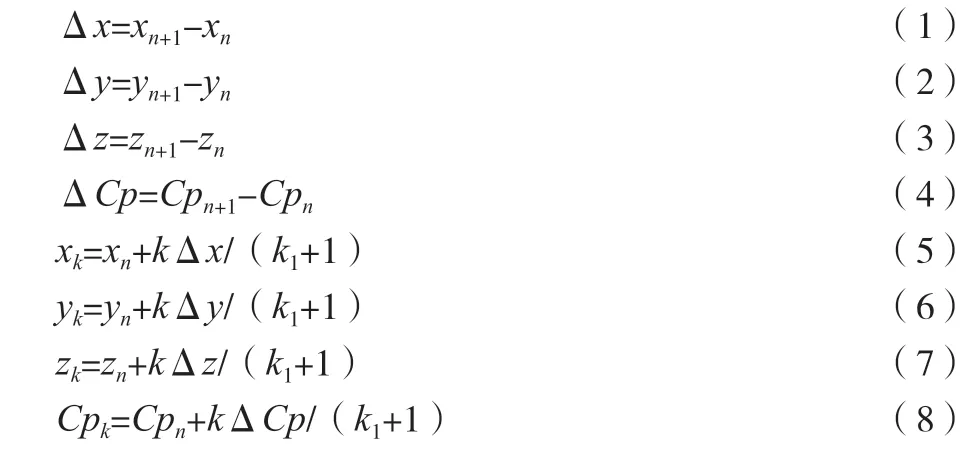
式中：xn、yn和zn为第n个压力点的坐标；xn+1、yn+1和zn+1为第n+1个压力点的坐标；xk、yk和zk为第k个压力点坐标；k为插值点编号；Cpn为第n个压力点的压力系数；Cpn+1为第n+1个压力点的压力系数。

以In点为起始，位置坐标每增加（Δx、Δy、Δz）/（k1+1），压力系数就增加ΔCp/（k1+1），直至In+1点，组成了一个In点到In+1的等差值数列，共k1+2个点，每两个点的坐标、压力系数差值为（Δx、Δy、Δz、ΔCp）/（k1+1）。

每行的点按上述离散方法进行离散，得到了一个全新的二维数组。列的加密和行的加密一样，可以将加密后的I行J列数组看成一个J行I列的数组，依旧对行进行离散得到最终的数组。上述CFD数据加密方法的核心是认为行（列）相邻点的压力系数是线性分布的，从而进行线性加密，为下一步计算做好准备。

1.5 等效到有限元模型

需要关注的有限元模型提供的信息包括每个网格的组成节点、每个节点的坐标。每个网格的组成节点信息关系到最后结果的输出格式（与该文无关，不再赘述）。每个节点的坐标信息是下一步计算的关键信息，任意节点记为节点k，坐标表述为（xk、yk、zk）。

求解任意节点坐标（xk、yk、zk）和离散后的每个压力点坐标（xc、yc、zc）的空间距离L，如公式（9）所示。

该处遵循的是编程的循环逻辑，给出判断标准距离L1，如果某一个压力点和有限元节点的距离L≤L1，那么就将压力点对应的压力赋值到有限元节点上，依次循环，直到找出最小距离对应的压力点。

完成上述步骤后，该文的核心算法就已经完成，可以描述为首先对CFD数据进行线性加密；其次，根据空间距离判断，将距离任意有限元节点空间最近的CFD数据网格点的压力系数赋值到有限元节点上。

2 验证

上述计算方法很容易编写成程序，为了验证程序的可靠性和该方法的可行性，使用程序对飞机的整流罩气动载荷进行分配，将分配结果与某数据处理软件的处理结果进行对比，部分压力点的对比如图2所示，应力云图如图3和图4所示，合力对比见表4。

表4 整流罩气动载荷合力

图2 部分压力点压力

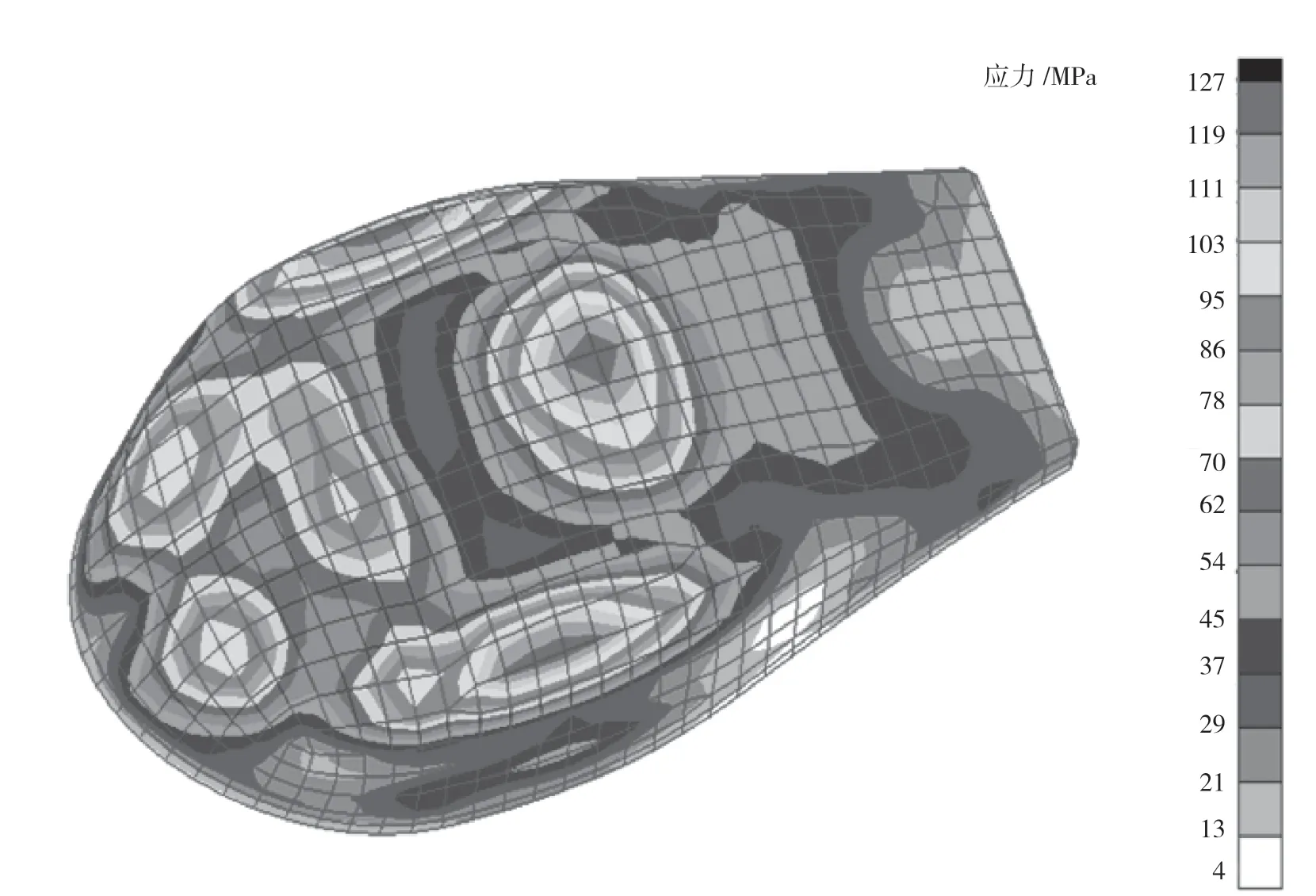
图3 线性插值应力云图

图4 某软件应力云图

从上述结果可以得出：2种载荷分配方法的单点压力平均误差约为4%，应力分布云图基本一致，主要力素合力误差约为3%，近似满足静力等效、分布等效原则。

3 结论

对该文研究的气动载荷分配方法进行程序化处理后，可以处理整流罩各种常用的压力分布数值或风洞测压气动数据，输出各CAE分析工具能够读取的载荷数据，且通用性较好，可以方便、快捷地用于类似整流罩结构的气动载荷分配，具有一定的工程实用价值。

但同时也面临一个问题，该方法只解决了整流罩强度分析所需要的载荷，后期还需要根据情况对整流罩罩强度试验加载载荷划分加载区域，将其转化为集中力，方便人为地对其进行不断迭代处理，下一步需要不断完善，从而实现试验加载载荷程序的功能。