一种单模光纤双高斯耦合透镜的设计与优化

李巍伟，陈 江，肖玉华，刘志栋，涂建辉

（兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000）

0 引言

激光冷却原子技术在真空计量与时间频率标准等精密测量领域有广泛的应用。利用单模光纤的柔性传输特性简化光路是冷原子装置小型化和集成化的必要选择[1-2]。单模光纤的模场直径一般为5～10µm，仅为多模光纤的十分之一[3-4]，由此增加了激光束和单模光纤之间的耦合难度，使耦合效率的提升成为冷原子装置小型化必须解决的重要问题。

耦合效率是耦合进单模光纤的能量与总能量的比值，耦合的实质是高斯光模场与单模光纤中激光传输模场之间的模式匹配[5]。在耦合面的同一空间位置，这两个模场均为类高斯分布，它们的振幅和相位越相近耦合效率越高。在实际的单模光纤耦合光路中，不仅模式匹配难以达到理想的匹配值，还因为单模光纤纤芯细，耦合透镜的衍射和像差会使高斯光的模场产生振幅衰减和不规则的畸变，造成耦合效率的损失。

耦合透镜的像差是限制单模光纤耦合效率提升的重要因素[6]。目前单模光纤普遍使用工艺成熟，成本低廉的球面镜作为耦合透镜，球面像差为主要像差，会严重影响耦合效率。如果不考虑像差因素，只考虑模式匹配，理论上理想耦合效率能超过80%[7]，但在实际中，单透镜的耦合效率往往只有20%～30%[8]，其原因除了实际透镜难以达到理想模式匹配的要求外，还有耦合透镜的像差和衍射效应引起的耦合效率损失[9]。像差中球面像差和彗差等初级像差会显著降低单模光纤的透镜耦合效率[4]。

针对耦合透镜的像差使得单模光纤耦合效率无法提高的问题，一种解决方案是采用非球面镜替代球面镜，通过矫正球差可以提升近20%[10]的耦合效率；另外，国外有研究者使用微透镜阵列作为耦合透镜，解决透镜球面像差问题，但是该方案存在微透镜设计和加工工艺复杂，制造成本高的问题[11-13]。由此发现，将一般用于矫正大视场、可变焦照相机和望远镜中像差的双高斯结构用于消除小视场、定焦距耦合透镜组的像差具有良好的效果。本文设计并优化一种双高斯耦合透镜，应用于铷冷原子装置中耦合传输波长780 nm、模场直径为5µm的单模光纤，期望用球面透镜基本消除像差对于耦合效率的影响，为单模光纤耦合透镜的设计和使用提供参考。

1 设计与优化方法

本文对双高斯透镜的设计与优化目标是消除球差等初级像差，抑制衍射效应，找到最佳的匹配焦距，给出耦合效率最高的设计方案。优化设计的思路是先在合理的范围内给定一组结构参数作为初始设计参数，对其进行迭代优化，得到一个像差最小的方案，计算其耦合效率；然后在焦距取值范围内通过改变光学面间的介质厚度，连续改变透镜组等效焦距，计算不同焦距点的耦合效率；最后得到一个耦合效率最高的方案。

采用ZEMAX软件设计了一个双高斯物镜作为铷冷原子装置的光纤耦合透镜，通过优化减小透镜组像差的方式提升高斯光与单模光纤的耦合效率。如图1所示，激光从物面至像面，一共经过12个光学面，用数字0，1，…，11表示，其中0和11面分别为物面和像面，4面为光阑面，1、2、5、6、8、9面为三组胶合透镜介质面，3、7、10为空气介质面。这些光学面的曲率半径和厚度作为双高斯透镜的结构参数，决定着透镜组的各种光学特性。本文的工作便是设计与优化这些结构参数。

图1 双高斯透镜结构图Fig.1 Schematic of double Gaussian lens

双高斯透镜的等效焦距是透镜组最重要的光学特性参数，设计和优化前须将透镜组视作一个单透镜确定其取值范围。图2为高斯光束通过单透镜耦合进单模光纤中的过程，其中l为物距，l'为像距，ω0为入射光束腰半径，ω'0为出射光束腰半径。

图2 单透镜耦合光路图Fig.2 Single lens coupling opticalpath

用F表示透镜焦距，λ表示激光波长，f表示高斯光的共焦参数，这些变量满足以下关系式[14]：

根据模式匹配，要得到较高的耦合效率，激光与单模光纤应该满足以下条件[7]：首先，光纤端面与出射光束腰位置重合；其次，耦合端面光斑半径小于光纤模场半径；最后，光束发散角小于光纤的数值孔径。此时，透镜焦距满足式（3）：

式中：d为光纤模场直径；ω(l)为透镜入射面上的光斑半径。焦距的取值范围可以作为透镜组设计和优化的边界条件。

根据ZEMAX操作手册并参考双高斯结构的设计可以提前给定一组在合理范围内的结构参数。但是，这样的初始结构参数具有随意性，一般像差很大，等效焦距也不在取值范围内，耦合效率极低，须进行预处理，即采用ZEMAX的光路自动优化设计功能将其等效焦距调整到式（3）的取值范围中，再对结构参数进行迭代优化来减小透镜组的像差。

在ZEMAX光路自动优化设计的过程中，因为采用了线性数值近似[15]，且求的是评价函数的极小值，所以算法收敛的结果是在初始结构附近找到一个评价函数变小的解，而这个解往往只是评价函数的极小值而非最小值。对此，本文对透镜组结构参数进行了分步迭代优化，以保证优化结果接近像差最小值。

将结构参数分成光学面曲率半径、玻璃厚度和空气厚度三类分步进行迭代优化。首先将光学面曲率半径作为变量，设置等效焦距为满足边界条件中的某一个值，运行优化程序，得到一个在该焦距下评价函数较小的设计方案。然后通过改变空气厚度得到一组光学面曲率半径和玻璃厚度相同、焦距不同的方案，比较它们的中心点点列图的方均根半径（RMS），找出中心点RMS最小的方案，再选出中心点RMS最小的焦距，将空气厚度、玻璃厚度设置为常数，物面、光阑面、像面之外的光学面的曲率半径设为变量进行优化迭代，进一步得到像差更小的方案，将其作为新的初始结构参数。重复上述过程，寻找新的RMS最小方案，其中玻璃厚度实际变化范围小，经过几次迭代后可将其视作与空气厚度相同的参数再进行迭代优化，收敛速度会更快，直到中心点RMS小于衍射光斑半径且不再减小，说明系统的像差足够小了，此时也同时得到一个能使像差最小的等效焦距。在此过程中，因为部分方案的焦距不同，不能直接使用评价函数作为像差大小的衡量标准，用中心点RMS来衡量系统像差的大小更为合理。

为了进一步探究透镜组的光学成像特性，用光学传递函数与包围圆能量分析函数对优化后的透镜组进行分析和评估。其中透镜光学传递函数从频率的角度能反映光学系统的成像特性，通过比较中心物点和边缘物点的光学传递函数图像的重合程度，可以反映透镜组不同物点位置的成像一致性。包围圆能量函数用来衡量光束经过透镜组后衍射光斑能量分布的情况。利用ZEMAX软件计算高斯光束和单模光纤传输模场的耦合，得到双高斯透镜的耦合效率，运算如式（4）[7]：

式中：PF为激光传输进入光纤中的光功率；PS为激光到达耦合端面的总光功率；U（r）和E（r）分别是激光在光纤中的传播模场和经过透镜变换后高斯光束的模场分布。

因为迭代优化后的像差足够小，但耦合效率不一定最高，所以还必须调节结构参数来改变等效焦距以进一步提高耦合效率。在这个过程中，为了避免结构参数改变过大，不再改变光学面的曲率半径，仅改变空气厚度和玻璃厚度，分别计算对应的耦合效率，直到找到耦合效率最高的等效焦距点，验证其像差是否足够小，否则须将此时的方案作为新的初始方案重新进行迭代优化，寻找最高耦合效率。

2 设计应用

针对铷冷原子装置耦合光束的特点，首先计算耦合透镜的焦距取值范围。光路中激光波长λ=780 nm，入射光斑半径ω（l）=1.00 mm，使用的光纤为保偏单模光纤，数值孔径NA=0.13，模场直径d≈5µm。将数据代入式（3）可以求得双高斯透镜组的等效焦距：F≤10.00 mm。因为耦合是一个汇聚光的过程，所以可以将0～10.00 mm作为等效焦距的边界条件。

参考光学设计手册和一般双高斯物镜设计方案，设定玻璃介质的厚度为2.000～20.000 mm、空气介质的厚度为0～1 000.000 mm作为边界条件，玻璃型号采用一般标准，除非在边界条件内的解不合理，否则不更改其型号。初步给定一组在合理范围内的双高斯透镜的原始参数，如表1所列。

表1 双高斯透镜原始参数Tab.1 Theoriginalparam etersof the double Gaussian lens

此时的等效焦距为16.30 mm，不在边界条件的取值范围内，必须对其进行预处理，将结构参数全部设置为变量，目标等效焦距设定为8.00 mm。表2是经过预处理后的结构参数。

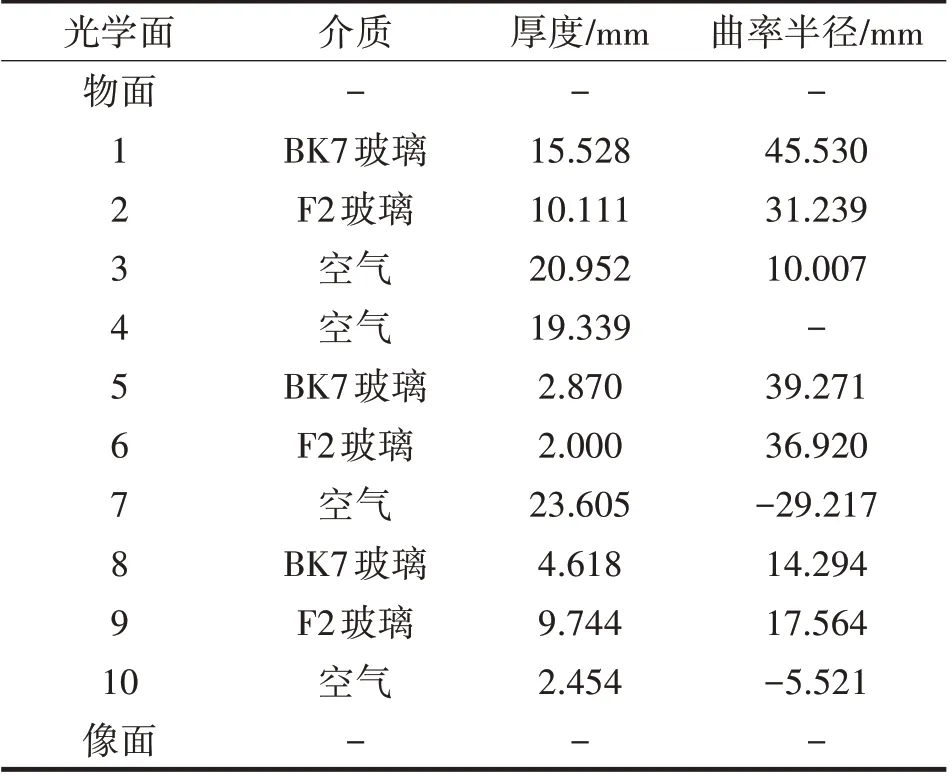
表2 双高斯透镜初始参数Tab.2 Initialparamentersof double Gaussian lens

先选定在透镜组的等效焦距取值范围内的一个焦距点8.00 mm作为透镜组初始结构预处理的目标等效焦距。将所有参数设置为变量，运行ZEMAX软件的优化程序，可以得到双高斯耦合透镜的初始设计方案。

对设计方案进行迭代优化，先不改变各光学面的曲率半径，仅将空气厚度（3、4、7、10面）4个参数设置为变量，改变透镜组的等效焦距，考查透镜组的像差大小。其次不改变透镜组的空气厚度与等效焦距，仅将9个光学面的曲率半径设置为变量进行优化，重复该过程，在进行空气厚度优化时将玻璃厚度（1、2、5、6、8、9面）也设置为变量进行迭代优化，直到中心点RMS不再减小。

图3是其中一个优化过程中RMS随等效焦距的变化曲线。由图3可知，随着等效焦距的增大，RMS一直在减小，当等效焦距为10.00 mm时，中心点RMS半径最小。连续几次优化过程均为等效焦距是10.00 mm的情况下中心点RMS最小，直至中心点RMS不再变小。此时结构参数如表3所列。由表3可以看出，10.00 mm的方案经过迭代优化以后，所有的参数比初始参数有了很大的变化。

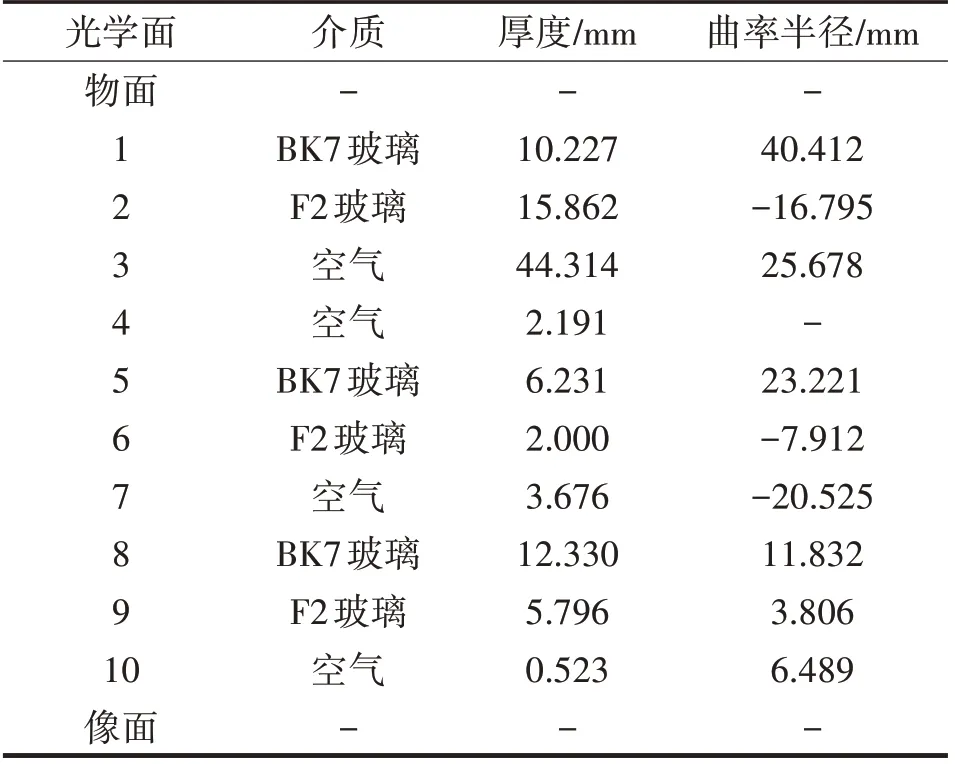
表3 双高斯透镜的优化参数Tab.3 Optimalparam entersof double Gaussian lens

图3 RMS随等效焦距的变化曲线Fig.3 Variation of RMS w ith equivalent focal lengh

为了更直观地比较成像质量的改善情况，计算了优化后透镜组的点列图，追迹了中心和透镜边缘3个点的光线，如图4所示。

由图4可以看出，中心像点弥散很小，RMS为0.009µm，远小于优化前，且弥散点分布均匀集中，没有畸变，成像质量提高明显；不同位置物点的点列图成像基本一致，说明不仅是球差，其他由入射光位置引起的彗差和像散等其他像差也被很好地矫正了。

图4 优化后的透镜组点列图Fig.4 Optim ized spotdiagram of lensgroup

图5为中心物点和边缘物点（归一化）对应的子午（T）和弧矢（S）共4条光线的光学传递函数曲线。从图中可以看出，各条光线的函数曲线在10-4精度内完全重合，且随频率的增大而平滑下降。这说明在透镜入射面上不同位置入射的光成像特性一致性良好，在实际光路中即使光束与透镜组轴线有小角度的偏差也不会增加透镜组的像差，有利于实验光路的搭建与调试。

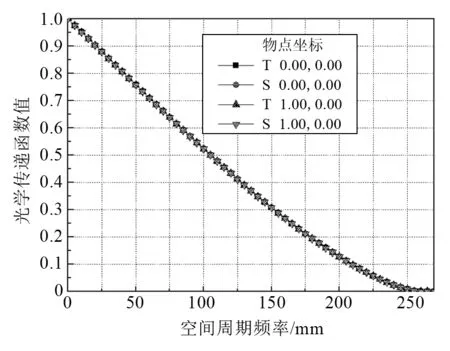
图5 中心物点和边缘物点对应的子午和弧矢共4条线的光学传递函数曲线Fig.5 The optical transfer function curve of four lines corresponding to themeridian and sagittalof the center and edge objectpoints

进一步分析了归一化视场中（0.00，0.00），（1.00，0.00），（0.00，1.00）三个物点发出的光线为主光线的包围圆能量示意图。从图6中可以看出，在10-4精度内，不仅六条追迹光线的函数曲线完全重合，并且与标准衍射光斑的函数曲线也完全重合，说明该光学系统已经接近衍射极限，基本消除了透镜像差对光纤耦合效率的影响。由于单模光纤的模场直径一般小于10µm，由图6可知，单模光纤的耦合效率极难高于90%，这与理论计算相吻合。

图6 归一化视物中3个物点的主光线的包围圆能量示意图Fig.6 The energy of the surrounding circle of themain light of three objectpoints in the normalized view

图7是在迭代优化过程中，等效焦距为10.00 mm方案的耦合效率随中心点RMS变化的情况。从图中可以看出，随着像差的不断减小，透镜组的耦合效率不断提高，当像差比较大时（RMS大于2µm），减小像差能使透镜组的耦合效率迅速提升。因此只要在改变焦距的过程中像差不太大（RMS小于0.5µm），即可以认为像差没有对耦合效率产生影响，透镜组的耦合效率迅速提升；当像差减小到一定程度后（RMS小于1µm），耦合效率不再有明显的提升。

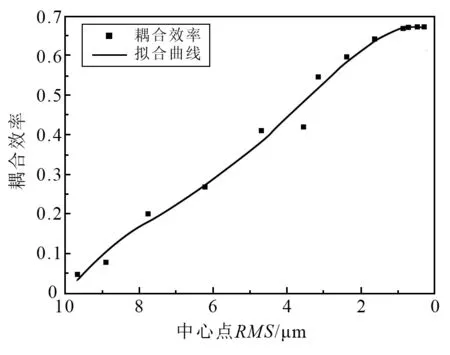
图7 等效焦距为10.00 mm的耦合效率随RMS的变化曲线Fig.7 The change of coupling efficiency w ith RMS when the equivalent focal length is10.00 mm

对优化的方案进行调整，耦合效率随着等效焦距的减小先增大后减小，在等效焦距为6.80 mm时达到最大值82.07%，如图8所示。此方案的RMS为0.121µm（远小于0.5µm），如图9所示。图8表明，此时耦合效率因为像差的增大而造成的损失可以忽略不计，因此无须再对6.80 mm的方案进行迭代优化，此方案可以作为双高斯透镜组的最终设计方案。

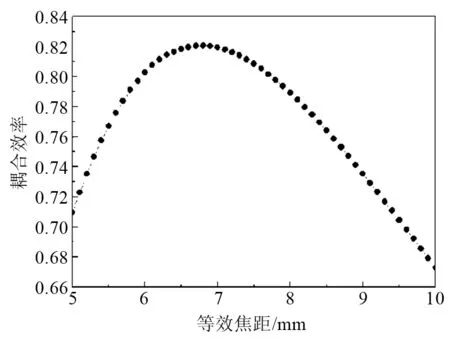
图8 耦合效率随等效焦距的变化Fig.8 Variation of coupling efficiency w ith equivalent focal length

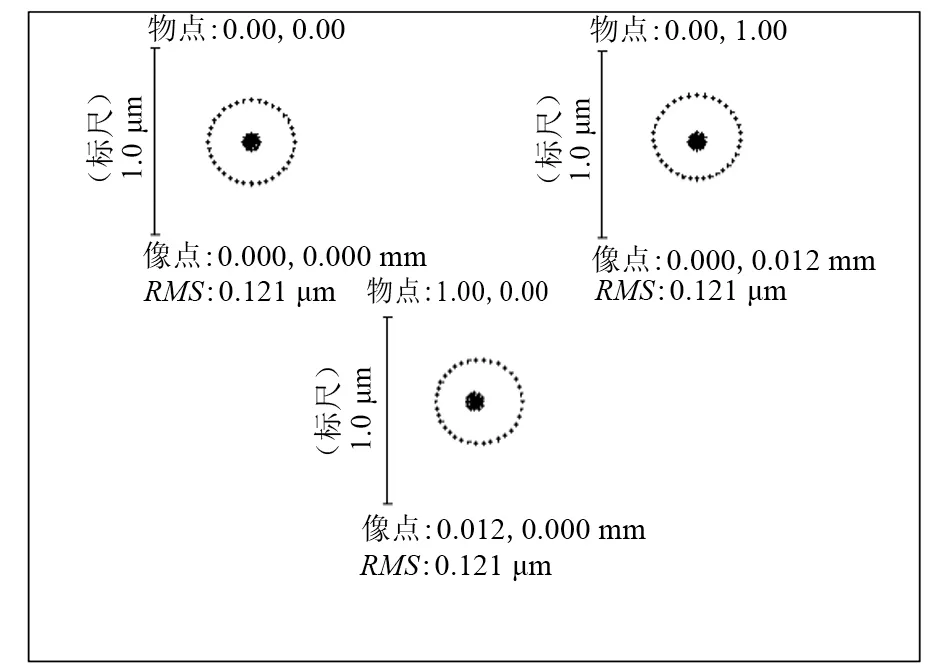
图9 耦合效率最高的透镜组点列图Fig.9 Optim ized spotdiagram of lensgroup w ith the highest coupling efficiency

图9是6.80 mm等效焦距时的点列图，其追迹的物点与图4的相同。对比图9和图4可以看出，经过结构参数调整，透镜组的像差虽然有了明显的增大（评价函数上升到10-5量级），但是仍保持在一个较低的水平，不同物点的点列图RMS值仍保持一致且无畸变，说明透镜组中心点与边缘成像的一致性未遭破坏。

表4是增加了透镜尺寸后等效焦距为6.80 mm的方案的结构参数，与表3相比，表4中介质厚度和第1个光学面的曲率半径不同，其他参数均相同。其原因是从10.00 mm的方案调整到6.80 mm的方案，主要是通过调整各介质的厚度实现的，但是只改变介质厚度无法使焦距发生如此大的变化，所以将第1个光学面的曲率半径也作为调整参数之一。由图9可知，这样的微调不会使透镜组的像差变差而影响成像的一致性，但是会对透镜的衍射效应产生影响，如图10所示。对比图6和图10可以看出，在像点中心2.50µm范围内的光斑能量占比更高，相当于衍射光斑被压缩了。

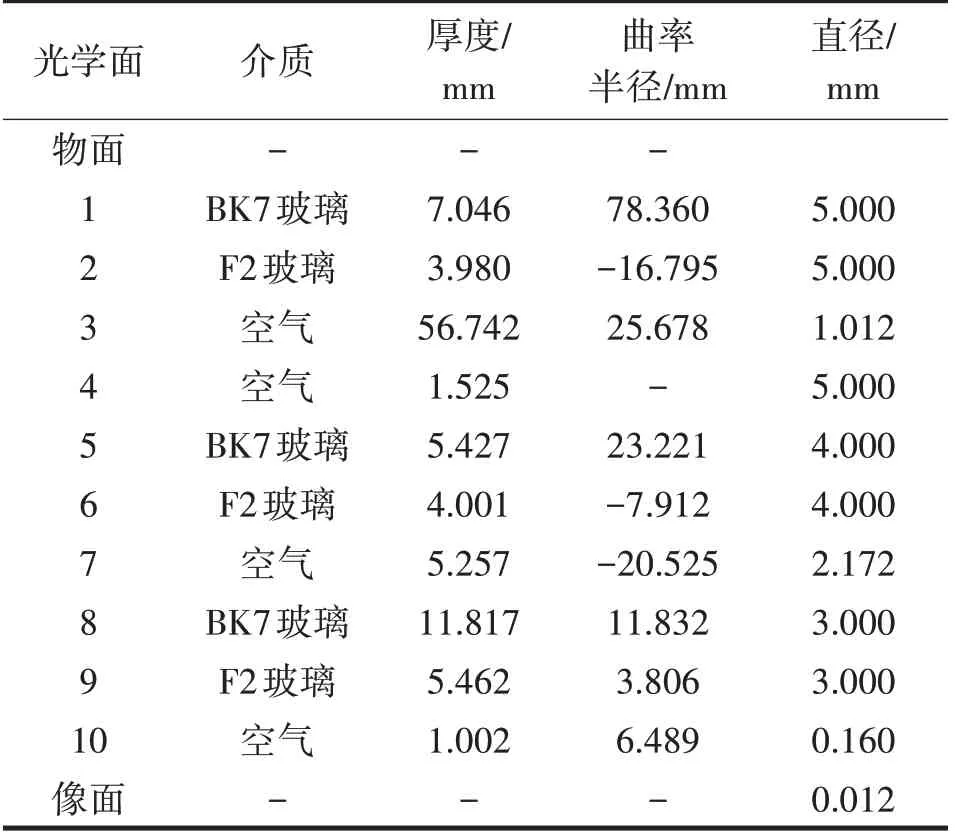
表4 双高斯透镜的最终参数Tab.4 Finalparam entersof doub le Gaussian lens

图10 耦合效率最高的包围圆能量示意图Fig.10 Schematic diagram of enclosed circle energy w ith the highestcoupling efficiency

3 结论

（1）为了消除像差的影响，得到耦合效率更高的单模光纤耦合透镜，提出一种双高斯透镜作为单模光纤耦合透镜的方案，光斑半径为1.00 mm的高斯光经6.80 mm的透镜组压缩至小于2.5µm后，耦合进模场半径为5.00µm的单模光纤。经过理论计算，其理想耦合效率为82.07%。

（2）对该方案的像差大小进行评估，得到10-5量级的评价函数和0.121µm的中心点RMS，基本消除了像差对耦合效率的影响。

（3）一般光学透镜通过先确定等效焦距和像差分配，再经过复杂的计算确定初始结构参数，然后分别对各种像差进行矫正和优化，与其相比较，利用透镜位置的变化调整焦距，再调整光学面的曲率半径来校准像差的方法，对透镜的设计与优化更为简单实用，对初始结构参数和等效焦距的要求不是很严格。本方法可以为单模光纤耦合透镜的设计和使用提供参考。

后续工作主要是开展透镜组的公差分析，通过实验验证进一步解决衍射效应对单模光纤耦合效率限制问题，以期能将耦合效率提升至90%以上。