不同温度下锂离子电池正极材料LiCoO2的第一性原理研究*

陈志强，崔 磊，杨丽娟

(宿迁学院 信息工程学院，江苏 宿迁 223800)

0 引 言

锂离子电池(LIBs)是最常用的便携式电子设备的储能装置(如移动式手机、笔记本电脑、电动工具和电动汽车等)[1-2]。在很大程度上，LIBs推动了移动革命，满足了人们对“移动生活”日益增长的需求。近年来，为了提高能量密度，降低LIBs的成本，大量的研究旨在为开发出新型正极材料并投入商业应用，比如LiMn2O4、LiFePO4、LiNi1-x-yCoxMnyO2、LiNi0.80Co0.15Al0.05O2(NCA)和xLi2MnO3·(1-x)LiMO2(M=Ni、Co、Mn等)[3-7]。其中，LiMn2O4、LiFePO4、NCM和NCA已被用于电动汽车(EV)和大型储能系统[8]。特别是LiFePO4在锂离子的脱出与嵌入过程中无体积变化，高温下不释放活性氧等特点应用更为广泛，而通过引入石墨烯对LiFePO4进行复合改性，以提高LiFePO4的倍率性能、克服碳包覆给LiFePO4的能量密度带来负面影响的研究也越来越多[9]。与其它正极材料相比，LiCoO2拥有众多独特的优势，包括高锂含量/电子导电率、高电化学稳定性、高密度及较长的循环寿命等[10]。正是由于这样的特点，LiCoO2即使已经诞生近30年，仍然是便携式电子产品市场上的主要正极材料。此外，LiCoO2在充电过程中通过提高上截止电压，还显示出能进一步提高能量密度的巨大潜力，比如LiCoO2在4.45 V下的能量密度为740 Wh/kg，在4.55 V下增加到840 Wh/kg，这几乎与与富锂正极相当。而考虑到LiCoO2的致密度远大于富锂正极的事实，基于LiCoO2的LIBs显示出更高的体积能量密度，这是作为便携式设备电源的压倒性优势。

由于锂钴优良的电化学性能，LiCoO2成为锂离子电池中应用最广泛的正极材料之一[11]。与其它正极材料(如LiFePO4、LiMnO2)生产的电池相比，使用LiCoO2正极生产的电池，虽然具有更佳的容量、更高的反应活性，但其热稳定性明显更差。这使得其在高温运行(>130 ℃)的情况下，LiCoO2电池更容易发生热失控或过充现象。因为在高温下，LiCoO2分解出氧气，而氧气随后会与电池内的有机物质发生放热反应。安全问题作为锂离子电池应用过程中的一个重要问题，随着更多的锂离子电池为获得更高的能量密度，电极材料变得高度氧化，并可能通过放热或吸热相变而降解[12]。为了提高可充电锂电池的热稳定性，了解正极材料在不同充电状态和温度下的热力学性质变得越来越重要[13]。

第一性原理计算已经被证明可以有效地预测各种材料的性质，包括嵌入电压、Li空位有序化、Li扩散、复杂过渡金属有序化以及电子输运路径等[14]。然而，在高功率下，电池由于高电流水平下的快速充电和放电产生了更多的热量，特别是当电池尺寸增大且许多电池相互连接形成系统时，导致一系列热力学问题出现。因此在研制大型锂离子电池时，应考虑温度对材料性能的影响。近年来，基于DFT的第一性原理计算在LIBs材料基态性质分析和预测中具有重要意义，目前已被广泛应用于材料电学和热力学性质的研究[15-17]。然而，大多数DFT研究只考虑了0 K下的热力学性质，并不包括在中等或高温下发生的物理和化学过程。由于温度对电池材料性能的影响，基态计算的预测性能与环境温度下实测的实际性能存在一定的差异[18]。例如，正极材料LiMn2O4在室温下具有立方结构，而第一性原理计算结果仅再现其低温下的正交结构[19]。LIBs电极材料在有限温度下的相变对电池的性能起着至关重要的作用，包括在高温或低温下中间相引起的电极材料的失效。另一方面，电池电压的准确预测与电极材料的吉布斯能量函数密切相关[20]。因此，为了准确描述LIBs正极材料的性能，需要对固定温度下的热力学参数进行估算。一定温度下振动配分函数对于热力学性质的研究具有重要意义，它的计算可以通过材料的晶格振动模型来获得。赵玉娜等[21]用第一性原理的方法研究了Li2NH的晶格动力学和热力学性质；刘波[22]采用基于密度泛函理论的第一性原理方法对层状二元锂过渡金属氧化物LiMn0.5Ni0.5O2、LiMn0.5Co0.5O2和LiCo0.5Ni0.5O2进行了系统地研究，结果表明采用不同的交换关联函数计算的声子色散曲线和热力学性质结果类似；周清清[23]采用基于DFT的广义梯度近似(GGA)中的PW91方法对LiNi0.5Co0.2Mn0.3O2进行第一性原理计算，结果表明温度和倍率是影响电池性能的关键因素，随温度和倍率的增加，电池首次放电比容量降低，电压平台降低。

层状LiMO2(M=Co、Mn、Ni)及其混合相是LIBs中广泛应用的正极材料，了解其热力学性质是研究LIBs的稳定性和容量的基础。本文旨在利用声子谱和晶格振动原理来计算锂离子电池正极材料LiCoO2的热力学性能。在计算过程中，首先，采用中子散射实验研究了晶体振动谱；其次，基于DFT，运用VASP计算出了Li、LiCoO2和脱锂后Li□CoO2声子谱；最后，获得了它们的熵和振动自由能等。此外，研究了晶格振动能对LiCoO2材料热力学参数的影响，并以LiCoO2/Li半电池为例，研究了振动自由能及脱锂电势改变量与温度之间的关系。

1 实 验

1.1 计算原理

在晶体材料中，存在着一种“晶格振动”的微观现象。该现象的存在是由于在晶体结构中，各原子之间存在着相互作用力，即每个原子振动时均会相互关联并通过传递能量，使整个晶格发生振动。本文的计算原理便是在“晶格振动”的基础上来了解锂离子电池正极材料LiCoO2的热力学参数。其基本原理描述如下：以晶体结构中存在N个原子为例来进行说明，其中以原子A处在晶体结构中的平衡位点，记为Rn，当晶体振动时，A原子将会偏移平衡位置，将此时该原子的位移矢量记为Un(t)，那么此刻A原子的位置即为Rn′=R+Un(t)。若当晶体结构振动幅度较小时，以与平衡位置的偏离程度作为总量，而分量则表示的是位移矢量，若晶体中有N个原子，便会形成3N个分量，写成ui(i=1，2…,3N)。N个原子晶系的势函数V可以表示为

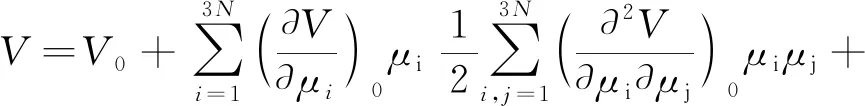
(1)

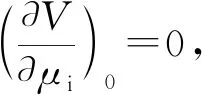
(2)

此时体系的势能函数只保留至μi的二次方程(简谐近似)。

1.2 模拟计算方法

DFT作为解析晶体材料物化性质的常用手段，在绝热条件下可以发挥出很高的应用价值，但理想条件下的模型研究，使得某些关键的热力学参数偏离了实际值，同时也让材料的进一步研究陷入了困局。基于此，为了更加精准模拟出材料处在不同温度下的热力学参数(电子熵、晶格振动自由能、晶格振动熵)，本文对目前存在的一些热力学模型进行修正，从而对材料在不同温度下所反映出的物理、化学性质进行准确预测，主要采用第一性原理计算声子谱的直接法、线性响应法来进行研究。

1.3 晶格振动谱的实验方法

晶体振动谱描述的是晶格振动频率与波矢之间的关系，也称为格波色散关系。当光子或中子进入晶体结构时，会与格波(频率为w的频率波)发生碰撞，从而出现能量交换的过程，导致光子或中子的散射。目前常见的晶格振动谱的实验测定方法分为中子散射和光子散射。其中光子散射实验中由于光子与声子能量差别较小，导致测量难度较大，而中子散射实验中不存在这一问题，因此本文选择中子散射实验。

中子散射的基本理论为：当动量和能量固定的光子束轰击晶体材料时，会与晶体原子核发生碰撞，在撞击过程中也会遵循动量守恒和能量守恒定律，由于入射中子的动量和能量是已知的，而从晶体表面散射出的中子的动量和能量也是可以测定的。若是选定某一方向的中子进行分析，便可以利用能量守恒和动量守恒方程(式(3))计算出该特定波矢的声子能量。因此只要将所有方向的中子散射谱搜集起来一一测量，便可以获得整个晶格振动谱。

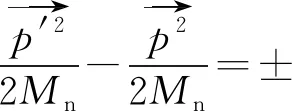
(3)

此外，中子轰击原子核的过程同样也遵循准动量守恒关系

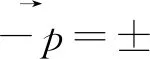
(4)

图1为中子三轴谱仪示意图。从图1可知，中子源为产生中子的核心，由反应堆制造出的慢中子流作为轰击粒子；单色器和分析器都是利用布拉格散射原理筛选出特定能量的中子，当检测的材料为单晶时，需要将样品旋转到一定角度才能获得有效数据；准直器在中子三轴谱仪中作为一种可选择性使用的配件，它由一排平行可以吸收中子的薄片组成，当中子流强度过大时，可以允许一定角度的中子通过，其一般被置于单色器和样品或样品和分析器之间。

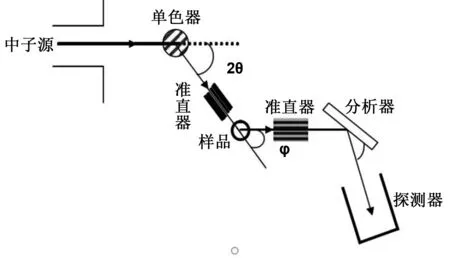
图1 中子三轴谱仪示意图Fig 1 Schematic diagram of neutron triaxial spectrometer

2 结果与讨论

2.1 锂原子的声子谱测试

为清楚地展现出晶格振动对锂离子系统脱锂电势的相关影响效果，进行了测试处理，确定了锂原子的声子谱参考标准，分别利用 ASP+Phonopy 与 PWscf对锂原子的声子谱进行了测试，结果如图2所示。

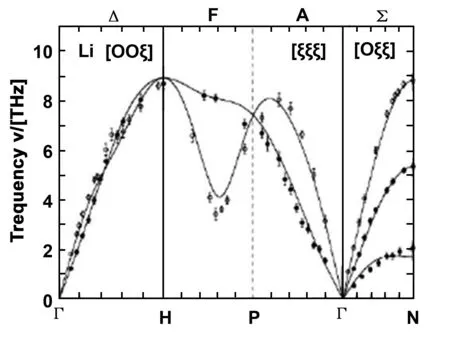
图2 锂原子的声子谱Fig 2 Phonon spectrua of lithium atom

基于所得到的单个锂原子的声子谱，确定倒空间路径为：Г→H→P→Г→N。进一步选取相同的倒空间路径，分别用 VASP+Phonopy 及 PWscf 软件进行测试，得到不同测试软件中的锂原子声子谱，结果如图 3所示。

从图3呈现的测试结果可以看出，在VASP+Phonopy 与 PWscf这两种不同的测试软件下，所得到锂原子声子谱结构具有较大差异，其中Г→H、H→P中的差异最显著。在VASP+Phonopy 的测试结果中存在分裂情况，且Г→H 区域3 条声子支发生了简并现象，但并未同时发生；在PWscf的测试结果中，Г→H 区域3 条声子支几乎完全重合，但在H→P 区域明显分离，分别呈现不同的变化效果。对比图2中的标准化图谱，可以发现VASP+Phonopy的测试结果更加契合标准图谱，即对于简单结构的声子谱计算，VASP+Phonopy能够得到更加准确的计算结果。

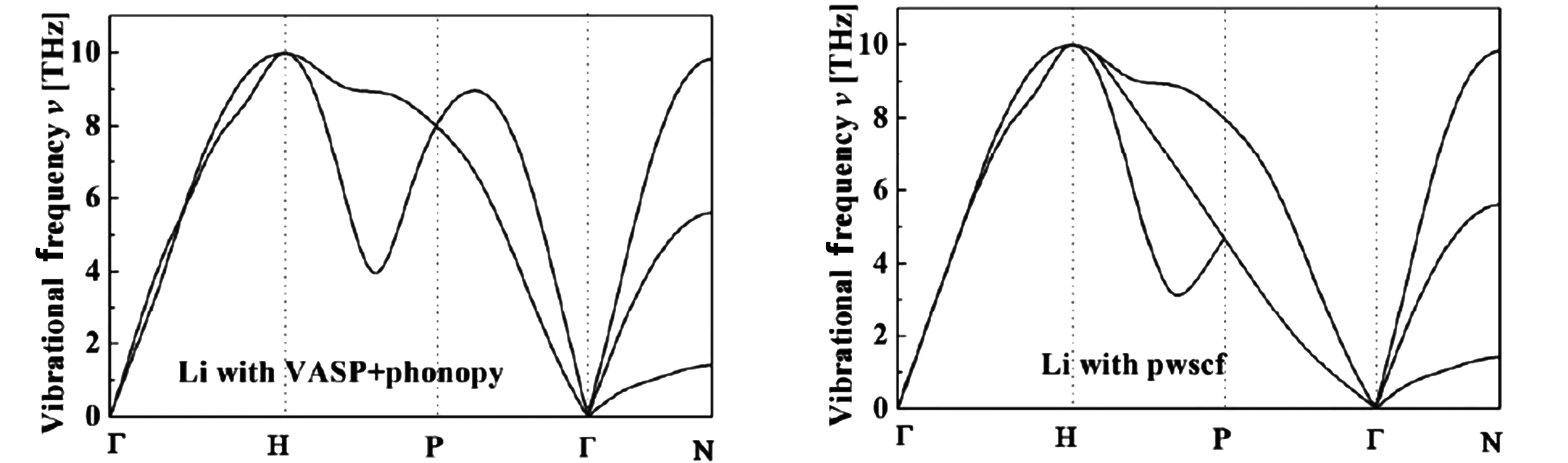
图3 不同测试软件中的锂原子声子谱Fig 3 Phonon spectra of lithium atom in different testing software

2.2 赫姆霍兹自由能对脱锂电势的影响

从第一性原理进行考虑，运用 VASP 软件计算热电材料性能具有较好的效果与优势，在一般情况下，其计算电极材料的平均脱锂电势如式(5)和(6)所示。

(5)

ΔG=GLix2MO2-GLix1MO2-(x2-x1)GLi

(6)

其中，f为法拉第常数；GLix2MO2和GLix1MO2分别为脱锂前后电极材料的吉布斯自由能。

在一般情况下，ΔG=ΔE+PΔV-TΔS≈ΔE-TΔS。同时，对处于稳定状态下的电极材料，ΔV变化量非常小，其相对几电子伏的基态能量的ΔE也是很小，所以可以忽略不计。然而通过DFT所计算出来的是0 K下的基态能量(TΔS)，因此在进行脱锂电势计算时，可以通过放弃考虑材料热力学性质对其的影响，来对计算公式进行简化以方便计算，但这同样也会对最终的计算值与实验值产生偏差，简化公式可表示为

(7)

为保证实验结果的有效性，将通过计入晶格振动产生的热力学量，对脱锂电势与相关热力学量的联系进行重新考虑，尽量将计算误差缩小化。而在计算吉布斯自由能差值时，不仅可以通过公式：ΔG=ΔE+PΔV-TΔS来进行计算，而且还可以考虑通过公式：ΔG=ΔE+PΔV进行计算。同时在合理地忽略了PΔV的取值后，可以近似得到：ΔG≈ΔF。因此，就可以建立起计算吉布斯自由能与赫姆霍兹自由能的联系，即将计算吉布斯自由能转化为计算赫姆霍兹自由能。

在分析一定温度下的所选电极材料的相关热力学性质时，会使用准谐近似(QHA)对赫姆霍兹自由能进行描述，其公式可以表达为

F(V,T)=E(V)+Fele(V,T)+Fvib(V,T)

(8)

其中，F(V,T)为赫姆霍兹自由能；E(V)为0 K时未计入零点振动能的基态能量；Fele(V,T)为在V状态和T温度(一般为低温)下，电子的热力学贡献；Fvib(V,T)为晶格的振动自由能，其计算过程可根据玻色-爱因斯坦统计法表示为

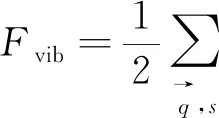
(9)

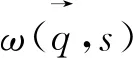
考虑材料的晶格振动引起的热力学量后，晶格振动前后的综合脱锂电势可以表达为

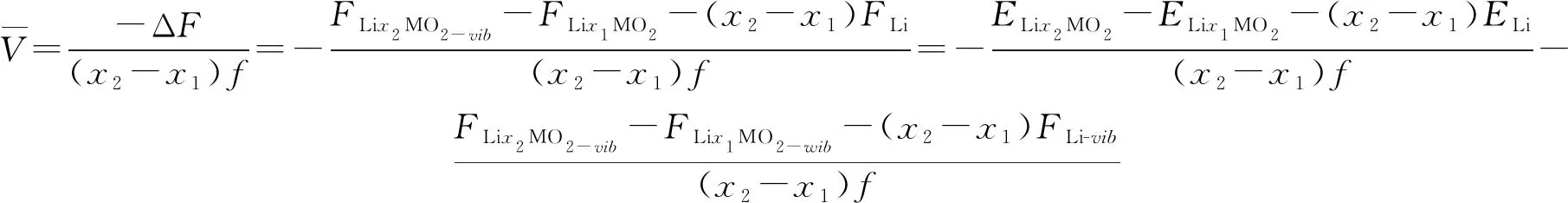
(10)

式(10)前半部分为晶格振动前的脱锂电势值的表达式，后半部分为晶格振动对脱锂电势影响的表达式。所以，在考虑了晶格振动影响热力学量变化的因素后，进一步确定出脱锂电势的改变量的表达式为

(11)

图4为Li、LiCoO2及Li□CoO2振动自由能及脱锂电势改变量与温度的关系。从图4(a)可以看出，从晶格振动色散谱得到的振动自由能与温度的关系呈现的变化趋势与F=U-TS中所反映的变化关系相同。即从零点振动能(0 K)开始，随着温度的不断上升，Li、LiCoO2及Li□CoO2的振动自由能取值逐渐减少，呈下降趋势，且三者的变化趋势一致。图4(b)为将零点时的能量贡献纳入考虑范围，计算出的LiCoO2/Li半电池系统在不同温度下工作效应的插层电位结果。由图4(b)可知，随着温度逐渐升高，插层电位逐渐降低。尽管温度效应的改变对潜在修正量的变化幅度影响不大，但呈现在电池系统的性能变化却非常明显。

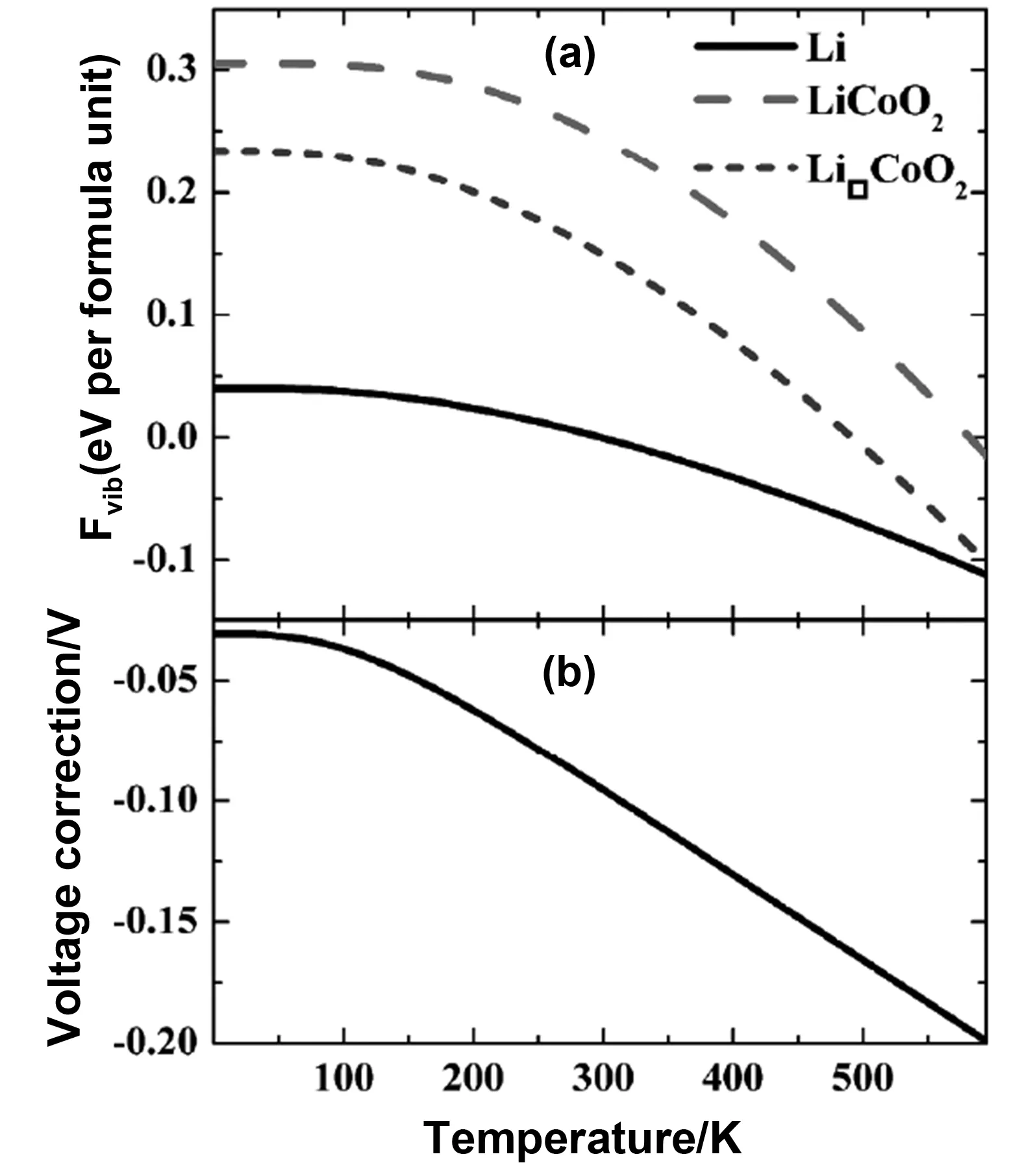
图4 Li、LiCoO2及Li□CoO2振动自由能及脱锂电势改变量与温度的关系Fig 4 Temperature dependence of vibration free energy and delithiation potential of Li,LiCoO2 and Li□CoO2

3 结 论

基于DFT，通过第一性原理计算研究锂离子电池正极材料LiCoO2的热力学性能，探究晶格振动及赫姆霍兹自由能对锂离子电池系统性能的相关影响。结论如下：

(1)晶格振动会对锂离子电池系统主要性能造成显著影响，且是不可被忽略的。通过VASP+Phonopy 软件对锂原子声子谱进行测试，结果表明锂原子声子谱结构存在分裂情况，且Г→H 区域3 条声子支发生了简并现象，但并未同时发生。

(2)计算并绘制了关于Li、LiCoO2及Li□CoO2的温度与赫姆霍兹自由能的关系，并根据温度变化所产的生不同影响对之前的脱锂电势进行了修正。研究发现从零点振动能(0 K)开始，随着温度的不断上升，Li、LiCoO2及Li□CoO2的振动自由能取值逐渐减少，呈下降趋势；且晶格振动会因温度的逐渐升高导致脱锂电势逐渐降低，进而致使电极材料的容量下降。