加筋土坡坡顶极限荷载的研究

乔丽平，杨 超

（1、深圳市龙岗地质勘查局 深圳518172；2、深圳市岩土综合勘察设计有限公司 深圳518172；3、五邑大学土木建筑学院 广东江门529020）

加筋土坡与无筋土坡相比具有施工高效、承载力高、造价低等优点，因此在工程中得到广泛应用。当加筋土坡处于极限破坏状态时，其坡顶所能承受的极限荷载是人们在设计中很关心的一个指标。对此，不少学者作了大量的理论分析和试验验证工作，WU［1］在墙顶用气袋施加荷载的方法对一高3 m的加筋土挡墙进行了破坏荷载试验；ZHAO［2］采用滑移线法对加筋土结构（加筋土坡、挡墙，加筋地基）的破坏荷载进行了研究；Richard 等人［3］运用大型室内试验揭示了土工格栅加筋土坡在坡顶荷载作用下的变形和破坏规律，并与未加筋土坡进行了对比分析；陶连金等人［4］通过足尺模型试验和FLAC 数值模拟，合理预测了土工格栅加筋边坡的坡顶极限荷载；高文华等人［5］在克服模型尺寸效应的前提下，建立了可用于分析和模拟室内足尺加筋土坡破坏机制的数值计算模型；胡耘等人［6］采用模型试验揭示了土工织物加筋黏性土坡坡顶加载的极限荷载规律；彭芳乐等人［7］应用传统塑性极限分析上限定理，导出了加筋砂土挡墙极限荷载上限解，并用模型试验结果进行了验证；雷胜友等人［8］对加筋砂土挡墙极限荷载及墙面横向位移进行了模型试验。

本文采用极限分析法分别应用传统塑性理论和广义塑性理论，推导了加筋土坡坡顶极限荷载的解析解，并与前人的试验结果进行比较。

1 基于传统塑性理论极限法的加筋土坡坡顶极限荷载

为简化计算，假设加筋土坡坡顶极限荷载均匀分布，假定以一过坡脚的斜平面为加筋土坡的破裂面。

1.1 外功率

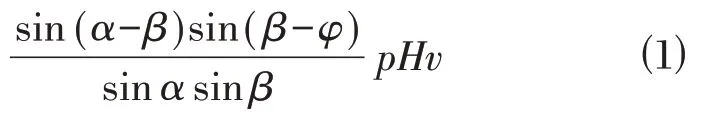
式中：γ为填土容重（kN∕m3）；H为坡高（m）；α为加筋土坡倾斜角；β为破裂面与水平方向的夹角；φ为填土内摩擦角；v为速度间断面上的速度间断量。

1.2 内能耗损率

内能耗损率包括土体的能量损耗率和筋材上的能量损耗率。沿着整个破坏面的土体能耗为：

如图1⒝所示，筋材上的能量损耗为［11］：

图1 基于传统塑性理论计算及筋材破坏Fig.1 Based on Traditional Plastic Theory Calculation and Reinforcement Failure

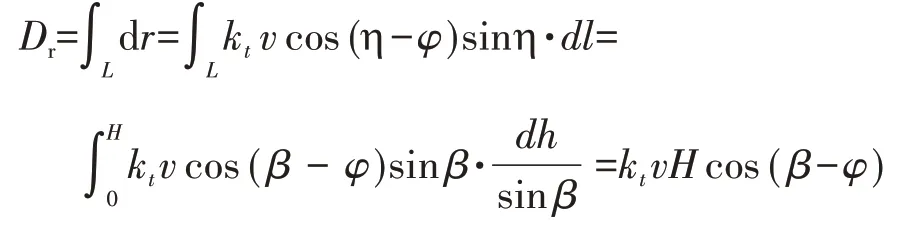
式中：η为筋材倾斜角；v为速度间断面上的速度间断量；kt为单位截面上的筋材拉伸强度，对于均匀分布的筋材，kt=nT∕H，其中T为筋材拉伸强度（kN∕m）；n为加筋层数。

将式⑴、式⑵代入虚功原理方程并整理得：

此时p取最小值。通过式⑷采用迭代法求出β，代入式⑶即可得到加筋土坡坡顶极限荷载p的最小值。

2 基于广义塑性理论极限法的加筋土坡坡顶极限荷载

2.1 外功率

广义塑性理论认为［9-13］：刚体平动时位移速度与刚体平面成φ∕2 夹角；转动破坏时，对数螺旋面上的位移速度矢量与对数螺旋面的切线间夹角为φ∕2 常量，即有=tan（φ∕2）。如图2⒜所示，外功率为：

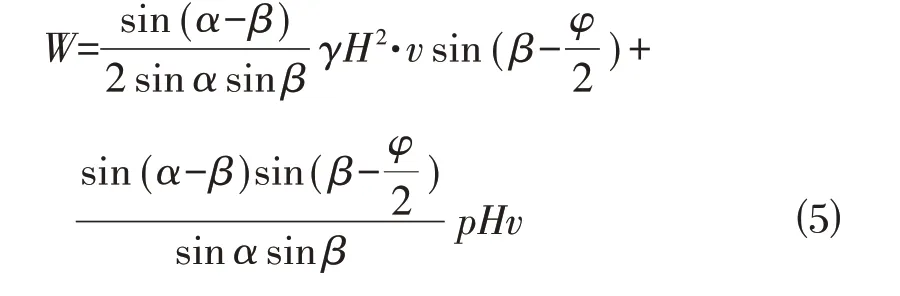
2.2 内能耗损率

土体沿破坏面的能量损耗率为：

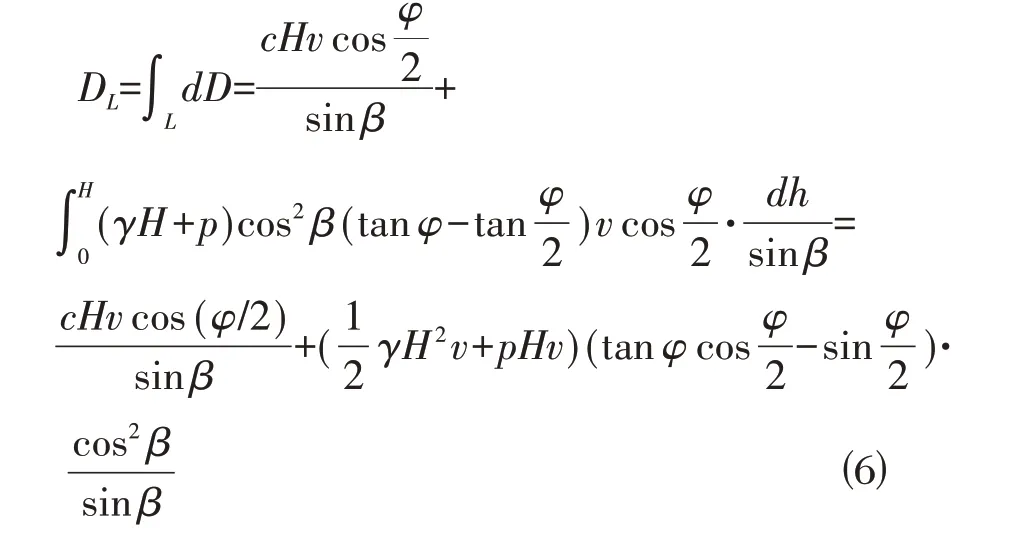
式中有关符号的定义同前。

如图2⒝所示，筋材沿整个破坏面的能量耗损率为：

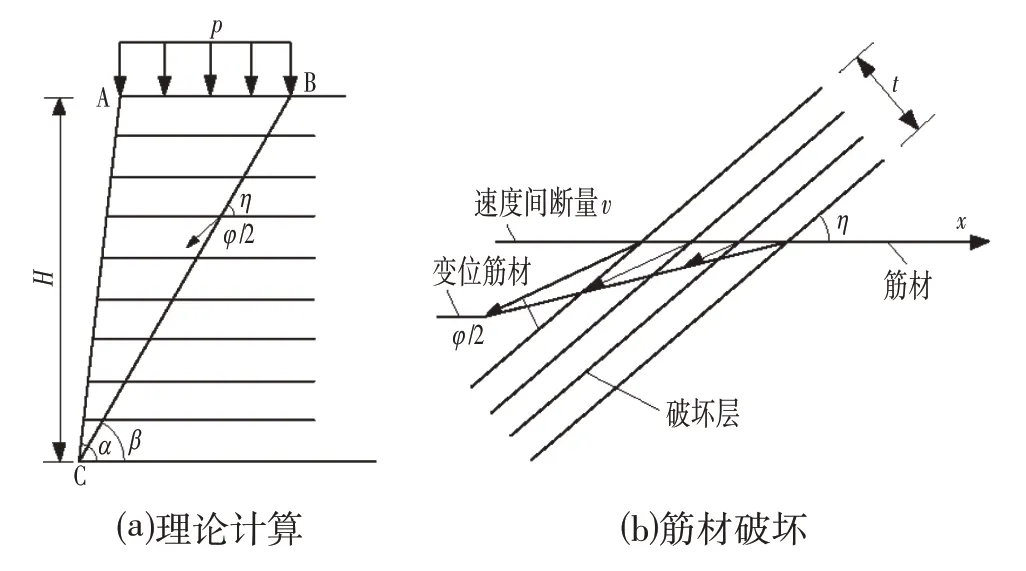
图2 基于广义塑性理论计算及筋材破坏Fig.2 Based on Generalized Plasticity Theory Calculation and Reinforcement Failure

将式⑸～式⑺代入虚功原理方程并整理得：

此时p取最小值。通过式⑼采用迭代法求出β，代入式⑻就可得到加筋土坡坡顶极限荷载β的最小值。

3 算例分析与讨论

3.1 砂性土（c=0）加筋土坡

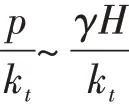
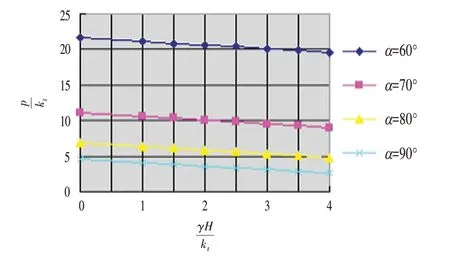
图3 传统塑性理论下曲线（φ=40°，c=0）Fig.3Schematic with Classical Plasticity Theory（φ=40°，c=0）

⑵当kt一定时，随着H的增大，p越小，即随着坡高的增加，坡顶所能承受的荷载越来越小，这与实际情况是一致的；

⑶当H一定时，p随着kt的增大将越来越大。但当kt增大到一定程度时，p逐渐趋于一定值。说明只增加筋材并不能一直提高土坡的承载能力，当加筋达到一定条件时，即使再增加筋材，也不能提高土坡的承载能力；

分析式⑻可以发现，当填料为砂性土时，由于φ较大，会导致式⑻中的分母项为负值，此时公式失效。分析其原因，是由于在运用广义塑性理论求土体能耗时，假定当土体处于极限状态时，保持体积不变，即不存在剪涨现象［9］，从而忽略了剪涨能耗对摩擦能耗的抵消作用。事实上当填料为砂性土时，是存在剪涨现象的。因此，当填料为砂性土时，建议不采用式⑻，而采用式⑶进行计算。

3.2 粘性土加筋土坡

文献［1］曾做了加筋土挡墙的破坏试验：墙高3 m，挡墙倾斜角α=90°，铺设了12 层无纺土工织物，其拉伸强度为T=6 kN∕m，墙顶采用气袋施加均布荷载；填料为粘性土，其重度为γ=18.9 kN∕m3，由CU 试验得c=82.74 kPa，内摩擦角φ=12.6°。分别采用式⑶、⑷和式⑻、⑼计算了该墙的破坏荷载，相应的计算值pcr与试验值如表1所示。

表1 加筋土坡坡顶极限荷载Tab.1 Ultimate Load on Top of Reinforced Soil Slope

由表1 可知：①两种方法计算得到的极限荷载相差不大（方法2略偏小），均与试验值较接近，说明当填料为粘性土时两种方法都是可行的；②分别采用两种方法求得的坡顶极限荷载相差不大，说明尽管传统塑性理论极限法在理论上有缺陷，但采用该方法计算得到的坡顶极限荷载基本可靠。而且采用这种方法忽略了摩擦能耗的复杂计算，大大简化了计算过程，尽管理论上不完善，但却非常实用。

4 安全系数取值的讨论

显然，实际工程中不能直接按式⑶、⑷或式⑻、⑼计算，应对其中的参数c、φ进行折减。

5 结语

⑴本文应用两种塑性理论，采用极限分析法推导了加筋土坡坡顶极限荷载计算公式，对于粘性土加筋土坡计算结果相差不大，均可作为加筋土坡设计时的参考，而对于砂性土加筋土坡则建议采用式⑶、式⑷进行计算。

⑵在应用广义塑性理论求土体能耗时由于假定土体不存在剪涨性，使得基于广义塑性理论极限法导出的公式对砂性土失效。

⑶本文对安全系数取值的讨论只是一个初步的工作，为使之更符合实际情况，可进一步进行相关研究。