压铸AZ91D镁合金表面涂层中Al2O3与TiO2金属间化合物的第一性原理研究

肖 睿，徐绍勇

(1.国家知识产权局专利局专利审查协作广东中心，广东 广州 510663；2.湖北理工学院 机电工程学院，湖北 黄石 435003)

0 引言

目前，镁合金被认为是实现汽车轻量化的最佳金属替代材料[1]。在汽车工业领域，由于镁合金同时具有减震性能优良、阻尼系数高的特点，主要用于制造离合器、发动机缸体和方向盘骨架等[2]。然而，镁合金存在硬度低、耐磨性差和防腐蚀性能低的缺陷，限制了其进一步发展[3]。当前，提高镁合金表面性能的方法主要包括自身材料改变法与表面涂层法。国内外关于表面涂层法的报道较多，主要集中在涂层与基体的结合强度、涂层的微观组织、不同工艺下硬度与耐腐蚀性观察分析研究。Al基复合涂层是提高镁合金表面硬度最常见的一种方法。王纯等[5]在AZ91D镁合金表面制备了一层Al层，与基体结合良好，无明显缺陷，涂层耐腐蚀性较好。马壮等[6]在AZ31B镁合金表面制备了Al2O3纳米涂层，使材料的耐磨损性能较母材提高了2.7倍，耐腐蚀性能与母材基体相比有明显提高。Celik等[7]在AZ31B镁合金表面制备了不同成分含量的Al2O3-TiO2复合陶瓷涂层，发现材料的硬度与耐腐蚀性均能大幅度提高。然而，从金属间化合物角度出发，探索不同体系涂层的晶体结构的研究较少。因此，本文以Al2O3-TiO2复合陶瓷涂层为分析对象，从晶体结构出发，采用第一性原理平面波赝势法，系统地研究Al2O3与TiO2金属间化合物的弹性性能、热力学性质和电子结构，为今后铝基复合材料提高镁合金表面硬度和耐蚀性提供一定的理论参考。

1 计算方法与模型

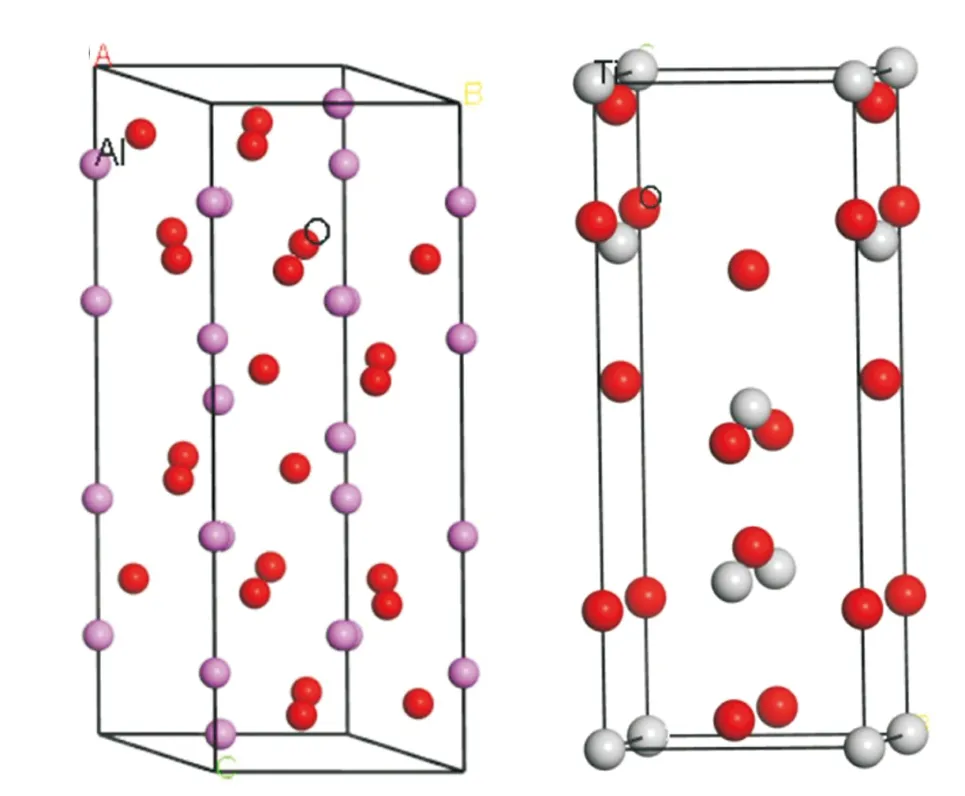
Al2O3的晶体结构为六方晶系，晶胞参数分别为a=b=4.7607 Å，c=12.9947 Å，α=β=900°，γ=1200°，空间群为R-3H；TiO2的晶体结构为四方晶系，晶胞参数分别为a=b=3.776 Å，c=9.486 Å，α=β=γ=900°，空间群为I41。TiO2的晶体结构模型如图1所示。采用基于密度泛函理论的Castep程序包[8]计算Al2O3和TiO2的形成热、结合能、电子结构和弹性性质。计算中，首先采用第一性原理GGA中的PW91方案[9]对原始胞进行结构优化，再对优化后的结构进行能量计算、弹性常数与电子结构的计算，其中Al2O3的平面波截断能为340 eV，K点为6×6×2，TiO2的平面波截断能为410 eV，K点为3×3×2，迭代收敛精度为1×10-6eV。利用Dmol程序计算不同温度下的热力学性质，用GGA中的PBE形式表示NVT电子交换能函数[10]，利用Fine网格散点和Smeating Energy进行能量快速收敛。对TiO2进行结构优化时，截断能为340 eV，K点设置为7×7×3，采用LDA下的CA-PZ方案进行结构优化，采用Fine网格散点和Smeating Energy进行能量快速收敛。

2 计算结果及讨论

2.1 形成热与结合能

计算参数直接决定了计算结果的准确性。为了保证本文计算参数的可靠性，首先对不同的晶格进行优化，将优化后的晶胞参数与实验参数进行比较，以得到准确的计算参数。经过优化计算，获得了Al2O3和TiO2的晶格参数(见表1)。由此可以看出，Al2O3晶胞的理论计算值与Finger[11]等的实验值误差为1.1%，TiO2晶胞的理论计算值与Schoberger[12]等的实验值误差为0.6%，误差范围<2%，说明本文选取的计算模型和计算参数可信。

表1 Al2O3和TiO2的晶格参数 Å

形成热与结合能是反映物质生成的难易程度及其稳定性的重要指标。合金形成热的计算公式为：

(1)

计算发现，Al,O和Ti晶体单原子能量的计算值分别为：-56.401 3，-430.107 2，-1 603.849 8 eV。Al2O3和TiO2的形成热与结合能见表2。合金形成热反映金属间化合物形成的难易程度。当形成热小于0时，说明化合物能稳定存在，而且绝对值越大时，说明这种金属间化合物越容易生成。由表2可知，Al2O3和TiO2可以稳定存在，且Al2O3比TiO2更易形成。

表2 Al2O3和TiO2的形成热与结合能

合金结合能的计算公式为[17]:

(2)

2.2 电子结构

Al2O3与TiO2的态密度图如图2所示。从图2中可以发现，在Al2O3的态密度分布图上，-20～-15 eV与-7～0 eV的价带区主要由O的d轨道贡献，-5～-1 eV的价带区，是由Al的p轨道贡献，导带区是由Al的d轨道贡献(见图2(a)(c)(e))。在TiO2的态密度分布图上，-57～-55 eV的价带区由Ti的p轨道贡献，-33～30 eV的价带区由Ti的s轨道贡献，-20～-15 eV与-5～0 eV的价带区由O的p轨道贡献，导带区由Ti的d轨道贡献(见图2(b)(d)(f))。另外，由图2还可以看出，对于Al2O3，费米能级EF处的态密度主要由O的d轨道贡献；对于TiO2，费米能级EF处的态密度贡献主要来自O的p轨道。此外，TiO2相态密度图相能带的宽度较大，离域性较强，成键较强；进一步分析得到，TiO2相对Al2O3较为稳定。

(a) Al2O3(b) TiO2

(a) Al2O3的氧原子分波态密度 (b) TiO2的氧原子分波态密度

(c) Al2O3的铝原子分波态密度 (d) TiO2的钛原子分波态密度

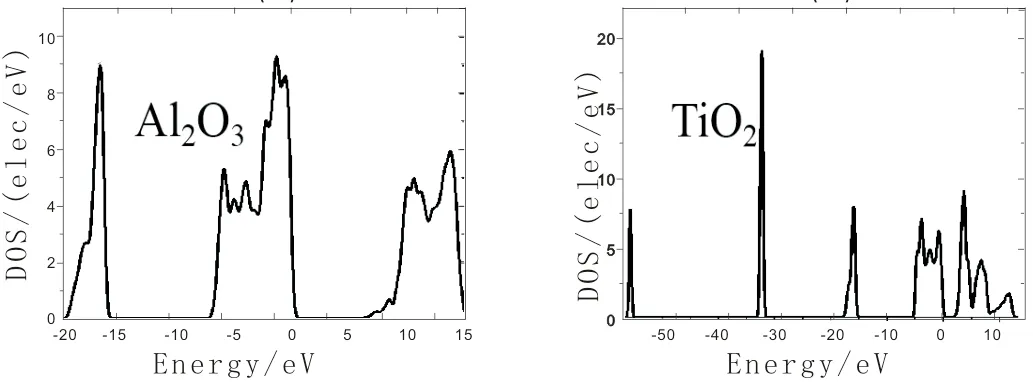
(e) Al2O3的总体态密度 (f) TiO2的总体态密度

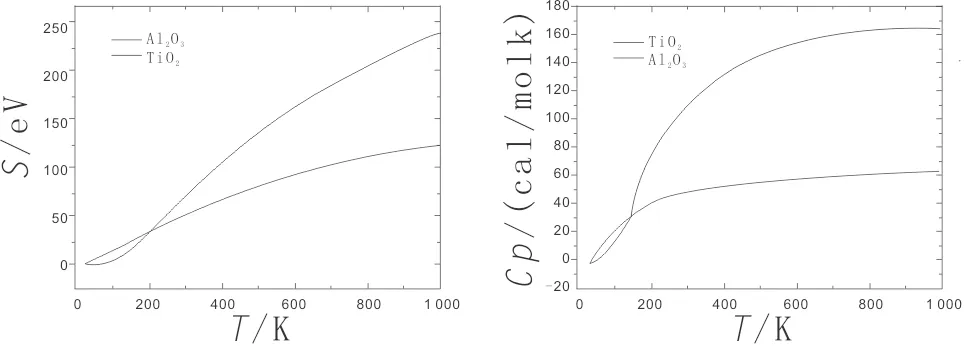
(a) 熵 (b) 热容

(c) 形成焓 (d) 吉布斯自由能

2.3 热力学性质

Al2O3和TiO2相的热力学性质如图3所示。由图3可知，这2种不同合金的热力学基本规律是相同的。在温度为0～1 000 K时，吉布斯自由能随着温度升高不断下降。对于Al2O3合金，在温度低于700 K时，吉布斯自由能为正值，表明在这个温服范围内Al2O3难以自发形成，热结构不稳定。对于TiO2合金，在温度低于425 K时，吉布斯自由能为正值，表明在这个温度范围内TiO2难以自发形成，热结构不稳定。在温度为700～1 000 K时，Al2O3和TiO2的吉布斯自由能均为负值，当温度升高时，2种金属间化合物的吉布斯自由能均在减小。在温度为700～950 K时，在相同温度下，TiO2相的吉布斯自由能始终最小。吉布斯自由能越小，相结构热稳定性越好[13]，表明TiO2在温度为700～950 K时的热结构稳定性比Al2O3好；在温度高于950 K时呈现不同的规律。

2.4 弹性性质

Al2O3作为六方晶系结构，有5个独立的弹性常数。TiO2作为四方晶系，有6个独立的弹性常数。Al2O3和TiO2的弹性常数Cij见表3。

表3 Al2O3和TiO2的弹性常数

弹性常数一般被用来判断合金的稳定性。同时，根据弹性常数Cij可以计算材料的力学性能。对于不同晶系材料，其评价标准不同，具体如下。

2)对于四方晶体，其力学稳定性的标准为[15]：C11-C12>0，C11+C33-2|C13|>0，2(C11+C12)+4C13+C33>0。

据表3可以推断，Al2O3和TiO2均满足相应的力学稳定性判断条件，表明Al2O3和TiO2的晶体结构是稳定的。

根据VRH算法，可以通过弹性常数Cij依次计算得到材料的常用弹性模量，例如：体积模量B、剪切模量G、Poisson比ν和杨氏模量E。具体计算式如公式(3)～(6)，计算结果列于表4。

(3)

(4)

(5)

(6)

这里重点探讨材料的常见力学性质包括硬度与脆性。一般可以通过弹性常数计算材料的各种模量来判断材料的力学性能。通常，杨氏模量和剪切模量越大，材料的硬度越高。Al2O3和TiO2的模量见表4。

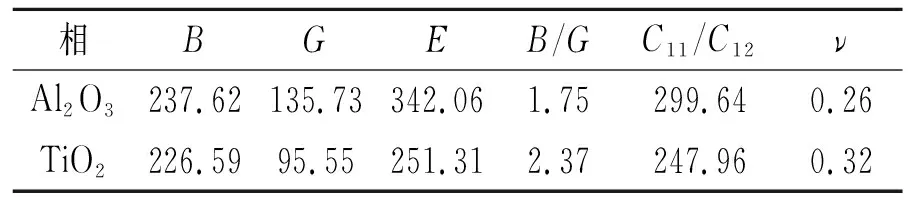
表4 Al2O3和TiO2的模量

由表4可见，Al2O3的剪切模量和杨氏模量均比TiO2的大，表明Al2O3是一种硬质相。此外，根据Jhi 等[16]的观点，材料的硬度与弹性模量存在正比例关系，弹性常数越大，材料的硬度越高。从表4中可知，Al2O3的大于TiO2的，其结果与前面模量预测结果一致。

材料的延性可以通过体积模量与剪切模量之间的比例关系间接得到。当B/G<1.75时，材料呈脆性，否则呈延性。计算所得Al2O3和TiO2的B/G分别为1.75和2.37，可预测Al2O3与TiO2均为塑性相。泊松比ν常用来评估材料结构抗剪切的稳定性参量，ν值越大，对应材料结构的塑性越好。因此，从表4可以看出，Al2O3的塑性较好。另外，C11/C12也是评估材料力学性能的一个重要参量，值越小，材料的塑性就越好。从表4进一步分析发现，这和B/G预测结果一致。

3 结论

本文研究了压铸AZ91D镁合金表面涂层中Al2O3和TiO2相的形成热、结合能、电子结构、热力学性质和弹性性质，发现Al2O3比TiO2相对容易形成，而TiO2相对Al2O3较为稳定；与Al2O3相比，TiO2结构稳定的原因是成键性较强；在700 ～950 K温度范围内，TiO2相的吉布斯自由能较小，其热结构稳定性好；Al2O3较TiO2相比塑性较好。