新情境题狂练

2021-08-04

新世纪智能(数学备考) 2021年6期

一、单项选择题

1.1943年19岁的曹火星在平西根据地进行抗日宣传工作,他以切身经历创作了歌曲《没有共产党就没有中国》,后毛泽东主席将歌曲改名为《没有共产党就没有新中国》.2021年是中国共产党建党100周年.仅从逻辑学角度来看,“没有共产党就没有新中国”这句歌词中体现了“有共产党”是“有新中国”的( )

A.充分条件

B.必要条件

C.充要条件

D.既不充分又不必要条件

2.2020年11月中国国际进口博览会在上海举行,本次博览会设置了“云采访”区域,通过视频连线,帮助中外记者采访因疫情影响无法来沪参加进博会的跨国企业首席执行官或海外负责人.某新闻机构安排4名记者和3名摄影师对本次进博会进行采访,其中2名记者和1名摄影师负责“云采访”区域的采访,另外2名记者和2名摄影师分两组(每组记者和摄影师各1人),分别负责“汽车展区”和“技术装备展区”的现场采访.如果所有记者、摄影师都能承担三个采访区域的相应工作,那么所有不同的安排方案有( )

A.36种 B.48种

C.72种 D.144种

3.2020年12月31日,国务院联防联控机制发布,国药集团中国生物的新冠病毒灭活疫苗已获药监局批准附条件上市,其保护效力达到世界卫生组织及药监局相关标准要求,现已对18至59岁的人提供.根据某地接种年龄样本的频率分布直方图(如下图),估计该地接种年龄的中位数为( )

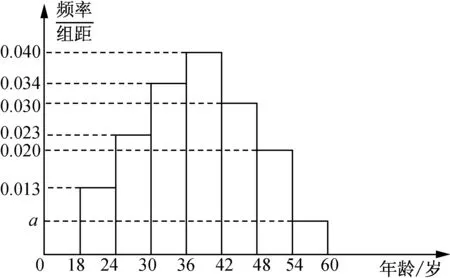
(第3题)

A.40 B.39 C.38 D.37

4.在新冠肺炎疫情期间,为有效防控疫情,某小区党员志愿者踊跃报名参加值班工作.已知该小区共4个大门可供出入,每天有5名志愿者负责值班,其中1号门有车辆出入,需2人值班,其余3个大门各需1人值班,则每天不同的值班安排有( )

A.30种 B.60种

C.90种 D.120种

5.调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图,则下列所有正确结论的编号是( )

注:90后指1900年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.

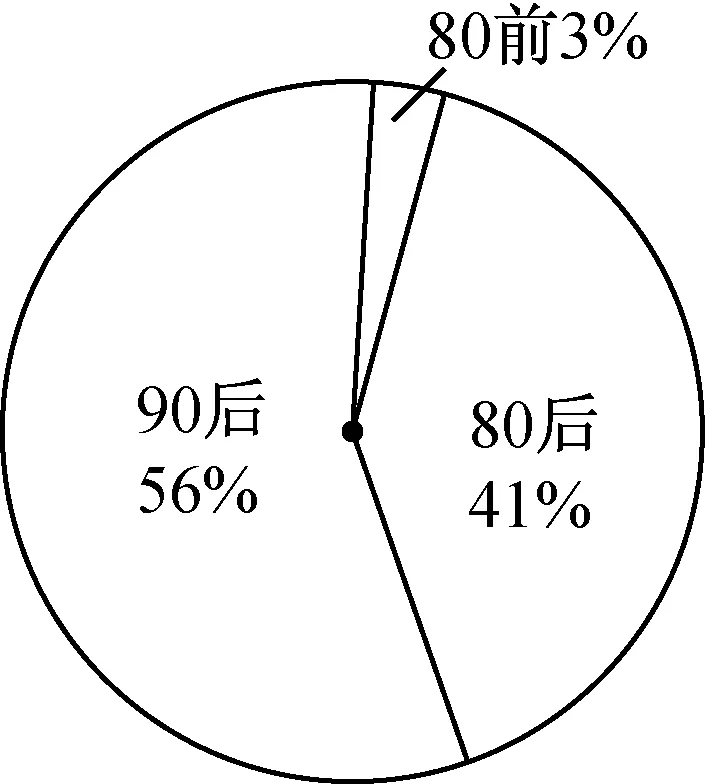
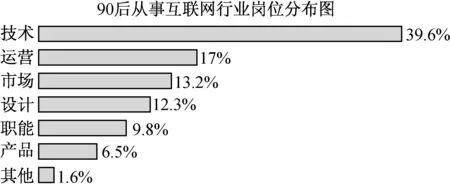
(第5题)

①互联网行业从业人员中从事技术和运营岗位的人数占总人数的三成以上；

②互联网行业中从事技术岗位的人数超过总人数的20%；

③互联网行业中从事运营岗位的人数90后比80前多；

④互联网行业中从事技术岗位的人数90后比80后多.

A.①②③ B.①②④

C.①③④ D.②③④

6.“阿基米德多面体”也称为半正多面体,是由边数不全相同的正多边形为面围成的多面体,它体现了数学的对称美.如图,将正八面体沿交于一顶点的三条棱的三等分点截去一个三棱锥,共可截去六个三棱锥,得到一个八个面为正六边形,六个面为正方形的“阿基米德多面体”,则异面直线AB与CD所成角的大小是( )

(第6题)

A.30° B.45°

C.60° D.120°

7.中国古代制定乐律的生成方法是最早见于《管子·地员篇》的三分损益法,三分损益包含两个含义:三分损一和三分益一.根据某一特定的弦,去其,即三分损一,可得出该弦音的上方五度音；将该弦增长,即三分益一,可得出该弦音的下方四度音.中国古代的五声音阶:宫、徵(zhǐ)、商、羽、角(jué),就是按三分损一和三分益一的顺序交益、连续使用产生的.若五音中的“宫”的律数为81,根据上述律数演算法可推算出“羽”的律数为( )

A.72 B.48 C.54 D.64

8.蟋蟀鸣叫可以说是大自然优美、和谐的音乐,殊不知蟋蟀鸣叫的频率x(每分钟鸣叫的次数)与气温y(单位:℃)存在着较强的线性相关关系.某地观测人员根据下表的观测数据,建立了y关于x的线性回归方程yˆ＝0.25x＋k,则下列说法不正确的是( )

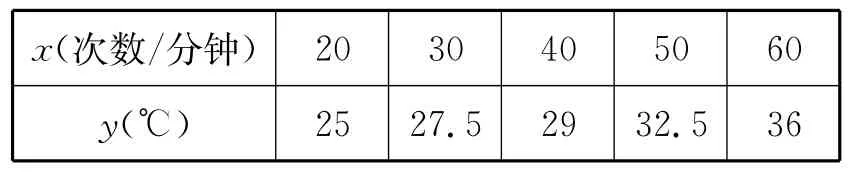
x(次数/分钟) 20 30 40 50 60 y(℃) 25 27.5 29 32.5 36

A.k的值是20

B.变量x,y呈正相关关系

C.若x的值增加1,则y的值约增加0.25

D.当蟋蟀52次/分鸣叫时,该地当时的气温预报值为33.5℃

9.某流行病调查中心的疾控人员针对该地区某类只在人与人之间相互传染的疾病,通过现场调查与传染源传播途径有关的蛛丝马迹,根据传播链及相关数据,建立了与传染源相关确诊病例人数H(t)与传染源感染后至隔离前时长t(单位:天)的模型:H(t)＝ekt＋λ.已知甲传染源感染后至隔离前时长为5天,与之相关确诊病例人数为8；乙传染源感染后至隔离前时长为8天,与之相关确诊病例人数为20.若某传染源感染后至隔离前时长为两周,则与之相关确诊病例人数约为( )

A.44 B.48

C.80 D.125

10.19世纪下半叶集合论的创立,奠定了现代数学的基础.著名的“康托三分集”是数学理性思维的构造产物,具有典型的分形特征,其操作过程如下:将闭区间[0,1]均分为三段,去掉中间的区间段记为第一次操作；再将剩下的两个区间分别均分为三段,并各自去掉中间的区间段,记为第二次操作；……如此这样,每次在上一次操作的基础上,将剩下的各个区间分别均分为三段,同样各自去掉中间的区间段.操作过程不断地进行下去,以至无穷,剩下的区间集合即是“康托三分集”.若使去掉的各区间长度之和小于则操作的次数n的最大值为( )

A.4 B.5 C.6 D.7

11.劳动力调查是一项抽样调查,2021年的劳动力调查以第七次人口普查的最新数据为基础抽取相关住户进入样本,并且采用样本轮换模式,劳动力调查的轮换是按照“2-10-2”模式进行,即一个住户连续2个月接受调查,在接下来的10个月中不接受调查,然后再接受连续2个月的调查,经历四次调查之后退出样本.调查进行时保持每月进入样本接受第一次调查的新住户数量相同.若从第k个月开始,每·个·月·都有的样本接受第一次调查,的样本接受第二次调查,的样本接受第三次调查,的样本接受第四次调查,则k的值为( )

A.12 B.13 C.14 D.15

A.(0,e-2) B.(0,e-2]

C.(0,e-1) D.(0,e-1]

二、多项选择题

13.对于数列{an},若存在正整数k(k≥2),使得ak＜ak-1,ak＜ak＋1,则称ak是数列{an}的“谷值”,k是数列{an}的“谷值点”,在数列{an}中,若an＝,下列数不能作为数列{an}的“谷值点”的是( )

A.3 B.2 C.7 D.5

14.意大利画家达·芬奇的画作《抱银貂的女人》中,女士脖颈上黑色珍珠项链与主人相互映衬呈现出不一样的美与光泽.达·芬奇提出:固定项链的两端,使其在重力的作用下自然下垂,项链所形成的曲线是什么? 这就是著名的“悬链线问题”,后人给出了悬链线的函数解析式:f(x)＝acosh其中a为悬链线系数,coshx称为双曲余弦函数,其函数表达式为coshx＝相应地,双曲正弦函数的表达式为sinhx＝.若直线x＝m与双曲余弦函数C1与双曲正弦函数C2的图象分别相交于点A,B,曲线C1在点A处的切线l1与曲线C2在点B处的切线l2相交于点P,则下列结论正确的为( )

(第14题)

A.cosh(x-y)＝coshxcoshy-sinhxsinhy

B.y＝sinhxcoshx是偶函数

C.(coshx)′＝sinhx

首先需要厘清一个问题，错误是否与瑕疵等同？如何进行区分？笔者以为可以从以下几个方面进行延展：首先是侵犯的形态方面，错误的严重性高于瑕疵的严重性，错误较为严重，瑕疵较为轻微；其次是违规的程序方面，错误在程序违反方面存在种类性，分为程序性错误和实体性错误两种，而瑕疵更多地是针对实体方面的内容；再次是产生的后果方面，错误较瑕疵而言更具有严重性……

D.若△PAB以A为直角顶点的直角三角形,则实数m＝0

三、填空题

15.春天是鲜花的季节,水仙花就是其中最迷人的代表之一.数学上有个“水仙花数”,它是指一个三位数,要求各位数字的立方和等于其本身.水仙花数共有4个,其中仅有1个在区间(150,160)内,我们姑且称它为“水仙四妹”,则在集合{142,147,152,154,157,“水仙四妹”}的6个整数中,任意取其中的3个整数,则这3个整数中含有“水仙四妹”,且其余两个整数至少有一个比“水仙四妹”小的概率是________.

16.在等腰三角形ABC中,AB＝AC＝2,顶角为120°,以底边BC所在直线为轴旋转围成的封闭几何体内装有一球,则球的最大体积为________.

17.我国古代人民早在几千年以前就已经发现并应用勾股定理了,勾股定理最早的证明是东汉数学家赵爽在为《周髀算经》作注时给出的,被后人称为“赵爽弦图”.“赵爽弦图”是数形结合思想的体现,是中国古代数学的图腾,还被用作在北京举行的第24届国际数学家大会的会徽.如图,大正方形ABCD是由4个全等的直角三角形和中间的小正方形组成的,若＝a,＝b,E为BF的中点,则用a,b表示＝________.

(第17题)

四、解答题

18.西尼罗河病毒(WNV)是一种脑炎病毒,通常是由鸟类携带,经蚊子传播给人类.1999年8—10月,美国纽约首次爆发了WNV脑炎.在治疗上目前尚未有什么特效药可用,感染者需要采取输液及呼吸系统支持性疗法,有研究表明,大剂量的利巴韦林含片可抑制WNV 的复制,抑制其对细胞的致病作用.现某药企加大了利巴韦林含片的生产,为了使生产效率提高,该药企负责人收集了5组实验数据,得到利巴韦林的投入量x(千克)和利巴韦林含片产量y(百盒)的统计数据如表:

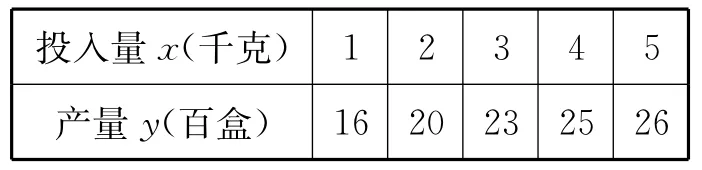
投入量x(千克) 1 2 3 4 5产量y(百盒) 16 20 23 25 26

由相关系数r可以反映两个变量相关性的强弱,|r|∊[0.75,1],认为两个变量相关性很强；|r|∊[0.3,0.75),认为两个变量相关性一般；|r|∊[0,0.3),认为两个变量相关性较弱.

(1)计算相关系数r,并判断变量x,y相关性强弱；

(2)根据上表中的数据,建立y关于x的线性回归方程为了使某组利巴韦林含片产量达到150百盒,估计该组应投入多少利巴韦林?

参考公式:相关系数r＝线性回归方程中,

19.随着生活质量的提升,家庭轿车保有量逐年递增,方便之余却加剧了交通拥堵和环保问题,绿色出行引领时尚,共享单车进驻城市.菏泽市有统计数据显示,2020年该市共享单车用户年龄等级分布如图1所示,一周内市民使用单车的频率分布扇形图如图2所示.若将共享单车用户按照年龄分为“年轻人”(20岁～39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,将一周内使用的次数为6次或6次以上的经常使用共享单车的称为“单车族”,使用次数为5次或不足5次的称为“非单车族”.