玩转高考真题
——概率篇
2021-08-04苏玖
苏 玖
真题再现 (2020·浙江卷16)一个盒子里有1 个红球、1 个绿球、2 个黄球共4个除颜色外相同的球,每次拿1 个,不放回,拿出红球即停,设拿出黄球的个数为ξ,则P(ξ=0)_______,E(ξ)______.
思维延伸先确定ξ=0 对应的事件,再求对应概率的结果;第二空,先确定随机变量,再求对应概率,最后根据数学期望公式求结果.
改编1
可以改编为求方差,于是有:
一个盒子里有1 个红球、1 个绿球、2 个黄球共4 个除颜色外相同的球,每次拿1 个,不放回,拿出红球即停,设拿出黄球的个数为ξ,则D(ξ)=______.利用方差公式的变形形式很快求解,由于展开化简可以得用它求解方差可以减少计算量.
改编2
真题中的黄球可以推广到n 个,于是有:
一个盒子里有大小、形状、质地相同的1 个红球,1 个白球,n个黄球(n≥ 2),每次从中任取一个球,不放回,直到取到红球为止,记取到黄球的个数为ξ,求ξ的概率分布列,数学期望和方差.
先利用挡板插空方法求出总的排法,第二步求红球前放k个黄球,然后将1 个白球放入前k+1个空位上,第三步求出红球前有k个黄球的概率,第四步利用期望与方差公式求解.
改编3
如果有两个白球,可以改编为:
一个盒子里有大小、形状、质地相同的1 个红球,2 个白球,3 个黄球,每次从中任取一个球,不放回,直到取到红球为止,记取到黄球的个数为ξ,求ξ的概率分布列,数学期望和方差.
求解本题的关键:一是求出这些球的总的排列数,二是正确求出红球前有k个黄球的排列数,白球可以放的位置有多少,这样就可以确定红球前有k个黄球的概率.
改编4
如果有m 个白球,n 个黄球,又可以得到:
一个盒子里有大小形状相同的1 个红球,m个白球,n个黄球,每次从中任取一个球,不放回,直到取到红球为止,记取到黄球的个数为ξ,求ξ的概率分布列,数学期望和方差.
求解本题的关键:首先从m+n+1 个位置选一个位置先放红球,再选出m个位置放白球,余下n个位置放黄球,求出所有的排列数;其次就是研究红球前有k个黄球的排列数,对于每一种红球与黄球的排列,利用插空法一个一个放入白球,每放入一个白球就多产生一个空挡,这样就可以求出黄球在红球前的排列数,即可求出相应的概率.
改编5
如果红球的个数为2 个,白球和黄球个数2 个或2 个以上,又可以得到:
一个盒子里有大小形状相同的2 个红球,2 个白球,3 个黄球,每次从中任取一个球,不放回,直到取到红球为止,记取到黄球的个数为ξ,求ξ的概率分布列,数学期望和方差.
抓住问题的本质,第一个红球前黄球的个数对应的排列数求法,第一个红球前黄球个数依次为0,1,2,3,但对于每一种情况,又要考虑白球的排列问题,在红球前白球的个数也是随机变量,即可以放0 个白球、1 个白球、2 个白球,利用排列组合知识即可求解.
改编6
对于随机变量的分布列也可以设置参数,满足一定条件,研究新的问题.
已知随机变量X的分布列为:
其中a,b,c为常数且成等差数列,求随机变量X数学期望的取值范围和方差的最大值.
利用分布列的性质和等差数列,将三元问题转化为一元(如用c表示a,b)问题,并求出c的取值范围,将数学期望和方差建立关于C的函数,最后利用函数知识求解.
改编7
也可以把等差数列改为等比数列,于是有:
已知随机变量X的分布列如表所示:
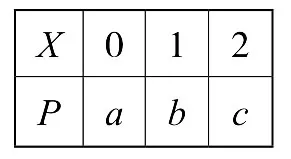
X 0 1 2 P a b c?
若4a,b,c成等比数列,则D(X)的最大值为( )
先建立a,b,c的方程组,再写出方差的表达式,观察变量之间的关系,再寻求求解策略.

做中悟道:从浙江的一道填空题出发,从如下几个层次进行改编,一是改编问题的方式,即将求数学期望改编为求方差,这样既复习数学期望公式,又复习方差知识;二是红球个数为1,对另两种颜色球的个数进行推广,如改编题2-4;三是增加红球个数为2 个,再研究分布列、数学期望与方差,这样问题的难度有所增加,需要有一定的数学思维能力才能完整解答;四是结合生活生产的实际情境和统计知识,如分层抽样方法,相当于先求出各种颜色球的个数,再利用古典概型求出分布列;五是在分布列中设置参数,结合代数相关知识求数学期望与方差的范围或最值问题,如改编题7,8.
点拨解析
真题:因为ξ=0 对应事件为第一次拿红球或第一次拿绿球,第二次拿红球,所以随机变量ξ=0,1,2,所以
改编1:由方差公式及真题解析的过程知,其中µ=Eξ(ξ),因此所以随机变量的方差为
改编2:ξ的所有可能取值为0,1,2,…,n.1 个红球,1 个白球,n个黄球排成一列有种排法.设第1 个红球前有k个黄球,k=0,1,2,…n,此时可看作将n个黄球排列后,红球只有1 种放法.n个黄球和1 个红球产生(n+2)个空档,选1 个位置放白球,有种排法.所以P(ξ=k)=分布列略.
改编3:ξ的所有可能取值为0,1,2,3.1 个红球,2 个白球,3 个黄球排成一列有=60种方法.
设第1 个红球前有k个黄球(k=0,1,2,3),其中这些排列中,在红球和黄球排列好后,有五个空挡.(1)我们从中选两个空挡各放一个白球,共有种方法,(2)选一个空挡放两个白球有=5种方法这样共有15 种方法.
P(ξ=k)=k=0,1,2,3.ξ的分布列略.
改编4:ξ的所有可能取值为0,1,2,,…n.1 个红球,m个白球,n个黄球(共m+n+1 个球)排成一列有种排列方法.
其中红球前有k个黄球(k=0,1,2,…,n)的排法是:
在红球和黄球排列好后,有(n+2)个空挡,选一个空档放一个白球,这时产生(n+3)个空挡,选一个空挡放白球,…,依次下去,共有(n+2)(n+3)…(n+m+1)种方法.
但是m个白球完全相同,无顺序性,所以共有种方法.
所以红球前有k个黄球的概率为P(ξ=k)=其中k=0,1,2,…,n.
分布列略,数学期望E(x)=
方差D(X)=
改编5:ξ 的所有可能取值为0,1,2.2 个红球2 个白球3 个黄球排成一列可以理解为,从7 个位置选2 个位置放红球,再从剩下5 个位置选2 个放白球,余下3 个放黄球,共有=210种方法.
(1)ξ=0,摸到红球前没有黄球,第一个红球前白球个数为0,1,2.所以有=84种方法.
(2)ξ=1,摸到红球前有1 个黄球,第一个红球前白球个数为0,1,2.所以有=63种方法.
(3)ξ=2,摸到红球前有2 个黄球,第一个红球前白球个数为0,1,2.所以有=42种方法.
(4)ξ=3,摸到红球前有3 个黄球,第一个红球前白球个数为0,1,2.所以有=21种方法.
所以P(ξ=0)=
改编6:由概率分布的性质得a,b,c∈ [ 0,1],a+b+c=1.①
又因为a,b,c为成等差数列,所以有2b=a+c②.
(1)E(X)=a+2b+3c=+2c,因为所以因此
改编7:依题意,有则b2=4c(1−b−c),即(b+2c)2=4c.
注意到E(X)=b+2c,E(X2)=b+4c,则D(X)=E(X2)−(E(X))2=(b+4c)−(b+2c)2=(b+4c)−4c=b.由基本不等式,得从而D(X)的最大值为当且仅当时取等号.故选项C 正确.
