裂缝对太阳能储热圆棒混凝土热性能的影响
2021-08-04朱慧君刘光鹏
朱慧君,匡 荛,刘光鹏
(东南大学 能源与环境学院,南京 210096)
目前,太阳能储热材料主要分为显热材料、潜热材料和化学材料[1-3]。显热材料包括液体材料(如熔盐、导热油等)和固体材料(如砂、岩石、高温混凝土等)[4-5]。混凝土的化学性能稳定、储热能力好、工作范围宽,并且每储热1 kW的成本在所有储热材料中最低,因此成为太阳能热发电的理想储热材料之一[1,6-7]。
混凝土在生产过程中会产生裂缝,这是无法避免的原始性缺陷。裂缝的主要影响因素有温度、原材料、塑性收缩裂缝等[8]。高温储热混凝土在放热过程经历较大的温度变化,热应力将是影响裂缝进一步发展的最主要因素。温度的大幅度变化造成裂缝处的热应力增加甚至超过极限开裂值,将会二次破坏混凝土的内部结构[9-10]。目前,对于混凝土裂缝的研究主要是定性分析。唐世斌等[11]通过对混凝土导热过程中热应力进行特征分析,得到温度梯度与热膨胀不匹配时热应力极容易导致混凝土开裂,同时开裂过程与导热系数密切相关;XIN J D等[12]通过实验研究了温度变化和约束程度对早期混凝土开裂行为的影响,建立约束程度与温差的关系,评估混凝土开裂的风险;BERTELSEN I M G等[13]在实验室规模上评估了混凝土中纤维对表面开裂程度的影响,得到纤维特性对控制裂纹形成有积极影响;RAJEEV P等[14]通过开发有限元模型,量化参数研究混凝土砖材料性能和热负荷的影响,发现砖内外表面温差与裂缝宽度呈正相关性;SHEN L等[15]基于热力学原理和混凝土破坏塑性,提出了一种在室温下具有特征性的热力学耦合模型,研究在裂缝热阻的效应下混凝土应力分布的情况。但是,对于裂缝的具体形状和尺寸与混凝土内部裂缝的温度梯度关系,仍未有定量研究。
考虑到前期研究主要围绕矩形裂缝[16],所以笔者以储热圆棒混凝土为例,对比研究存在弧状裂缝和弦状裂缝时的混凝土放热特性,并从裂缝的圆心角、宽度和位置进行数值分析,给出裂缝温差(放热过程中某时刻裂缝中的最大温差)在放热过程中的变化曲线。利用拟合函数确定裂缝温差峰值与裂缝参数的关系,从定量角度分析混凝土在热应力极限情况下裂缝参数的安全范围,为预防和控制混凝土裂缝的研究提供参考。
1 计算模型
1.1 数值模型
图1为所研究对象的数值模型均以裂缝的内边界作为裂缝特征位置,其中:φ为裂缝圆心角,(°);δ为裂缝宽度,mm;x为裂缝位置特征长度,mm。
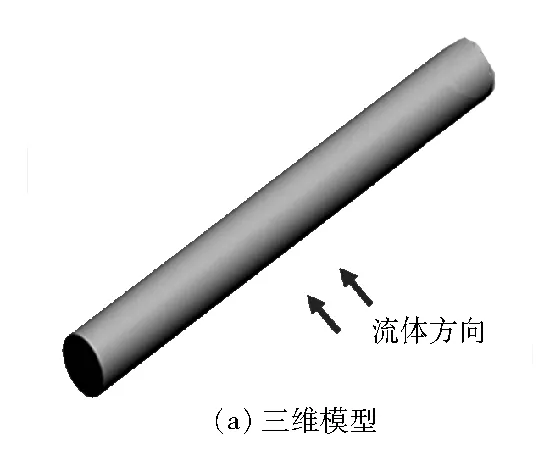
图1 数值模型
传热介质为导热油,横掠混凝土圆棒进行热交换。由于混凝土的导热系数低,可忽略其轴向温度变化,将三维模型简化成二维模型。研究在放热条件下,不同圆心角、宽度和位置的裂缝对混凝土内部温度分布的影响,以及裂缝处温差变化对混凝土热应力的影响。从储热模块到外部环境没有热损失,因为模块通常采用良好的隔热。
1.2 计算条件
假定放热过程中各工质的物性参数为常数,材料物性参数见表1[17],在典型工况下进行数值模拟。混凝土初始温度为390 ℃,导热油的进口温度为290 ℃、流速为0.004 m/s,经计算可得对流传热系数为32.97 W/(m2·K)。在低温导热油冷却高温混凝土的过程中,混凝土的温度随时间不断变化,属于非稳态传热过程,所以选用瞬态热分析法进行计算,时间设置为2 000 s。
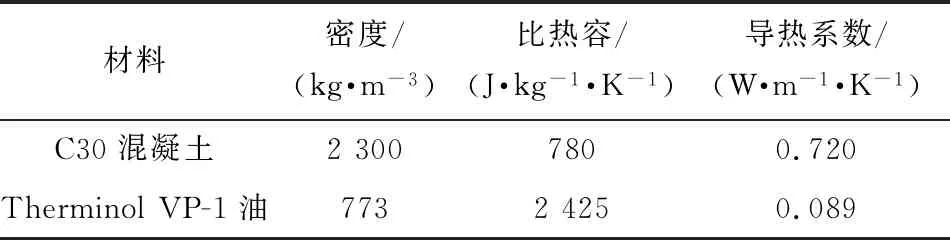
表1 材料物性参数
2 理论分析
2.1 传热机理
混凝土放热过程中,包含导热、对流和辐射。根据刘光鹏等[16]的研究结果,在混凝土裂缝中,对流传热量、辐射传热量远低于导热传热量,因此在研究中以导热为主。将非稳态导热微分方程应用于该问题,方程为:
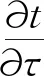
(1)
式中:t为温度,℃;τ为时间,s;a为热扩散系数,m2/s。
2.2 热应力的理论计算
理想条件下混凝土无裂缝,内部温度均匀变化时,热应力可处于稳定的安全值。但是,由于在原混凝土制造过程中,内部冷却不易均匀,储热混凝土中,必定存在裂缝。高温放热过程中,混凝土内部温度梯度大,裂缝处的温差由于空气热阻的存在而明显高于其他部位,因此裂缝处由温差引起的热应力也将更大。当裂缝局部的热应力大于混凝土的极限热应力时,混凝土会在裂缝处二次开裂,降低传热效果,甚至危害设备运行安全。
根据混凝土结构的二维温度应力的计算过程,最大温度应力σmax[18]为:
(2)
式中:H(τ)为与时间有关的应力松弛系数,取0.327;α为线膨胀系数,K-1;Δt为裂缝温差,K;μ为泊松比,取1.5;kr为约束程度函数,采用完全约束时为1;C为阻力系数;E为弹性模量,Pa;L为圆棒长度,m;B为圆棒直径,m。
选取C30混凝土作为研究对象,混凝土圆棒的直径为80 mm,线膨胀系数为1×10-5K-1,弹性模量为3.0×104MPa。根据GB 50010—2010《混凝土结构设计规范》查得,混凝土30 d龄期的抗拉强度为2.01 MPa。
裂缝温差决定混凝土裂缝处的热应力,而热应力是决定高温储热混凝土是否会二次开裂的直接因素。当混凝土内部最大裂缝温差为24.105 K时,内部热应力达到2.01 MPa,此时混凝土进一步开裂。但不同圆心角、位置和宽度的裂缝对于混凝土热应力的影响尚不清晰,需要对其进行数值模拟计算,得出混凝土的温度分布,这有助于对储热模块放热性能进行优化。
3 结果与分析
3.1 裂缝圆心角的影响
从具有计算意义的小圆心角(5°)开始选取10个圆心角,设置裂缝的宽度为2 mm、位置特征长度为20 mm进行模拟,以期得到裂缝圆心角对于混凝土温度分布的影响。图2为圆棒混凝土放热2 000 s的温度分布。


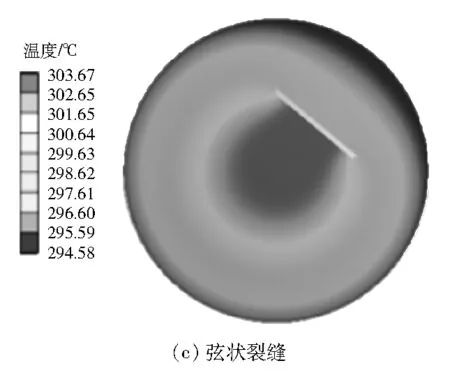
图2 混凝土放热2 000 s的温度分布
由图2可得:无裂缝时,圆棒混凝土中心温度最高,沿半径方向逐渐降低;存在裂缝时,混凝土仍以导热方式向外发散热量,但由于裂缝内空气热阻的存在,热量传递的路径发生变化,高温中心向裂缝移动,更多的热量直接由内部的混凝土传递给流体,不经过裂缝;相比于裂缝外边界,内边界的导热路径更长、热阻更大,因此内边界温度高于外边界温度。
图3为不同圆心角时圆棒混凝土的裂缝温差随时间的变化。
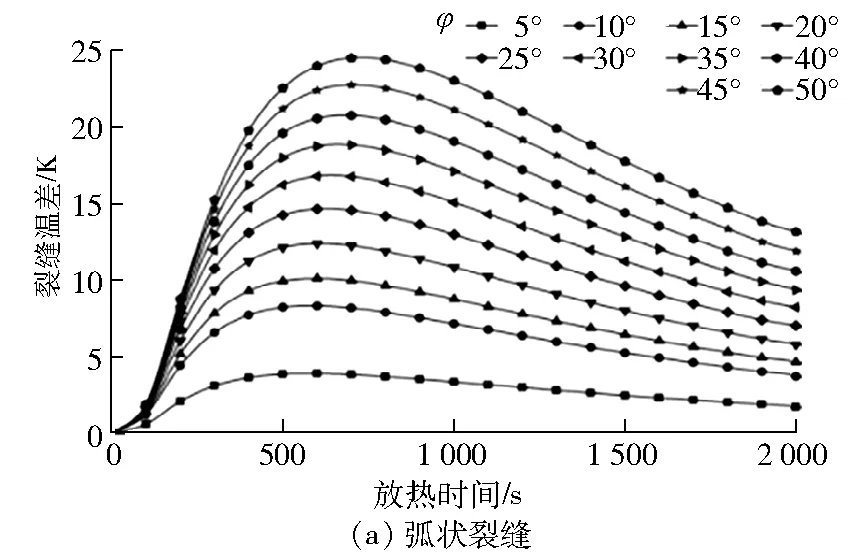
图3 不同圆心角时裂缝温差随时间的变化
由图3可得:随着放热的进行,两类裂缝处的温差均先呈现快速增长,到达峰值后逐渐缓慢降低。这是由于裂缝中空气热阻远大于混凝土导热热阻,热量大多直接通过混凝土传导至外界。与内边界相比,裂缝外边界向外界导热路径更短,热量快速散失后稳定在低温;内边界由于有更长的导热路径,热量散失缓慢并且稳定。当圆心角变大时,弧状裂缝的弧度变长,裂缝温差呈现递增趋势。圆心角从5°到10°时,裂缝温差整体增加了5 K左右,增加较大;圆心角为10°~50°时,各区间裂缝温差变化仅约为2 K。在放热过程中,弧状裂缝和弦状裂缝的温差变化趋势一致,但弧状裂缝温差略大于弦状裂缝温差,原因是对于相同的圆心角,弧状裂缝两侧的传导路径差值比弦状裂缝的更大。
3.2 裂缝宽度的影响
选取裂缝的圆心角为35°、特征位置长度为20 mm,研究裂缝宽度对裂缝温差的影响。图4为不同裂缝宽度时裂缝温差随时间的变化。由图4可得:随着放热时间的增加,裂缝温差全部呈现先快速增加至峰值而后缓慢降低的趋势。这与图3曲线的趋势一致,其原因也相同。

图4 不同裂纹宽度时裂缝温差随时间的变化
3.3 裂缝位置的影响
选取裂缝的圆心角为35°、宽度为2 mm,研究裂缝位置对裂缝温差的影响。图5为不同裂缝位置特征长度时裂缝温差随时间的变化。
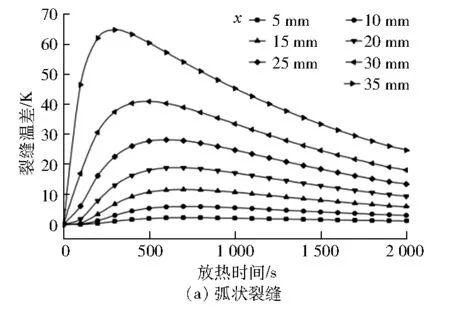
图5 不同裂缝位置特征长度时裂缝温差随时间的变化
由图5可得:针对弧状裂缝,当裂缝位置特征长度≤5 mm时,裂缝温差基本没有变化,是因为裂缝足够靠近储热圆棒中心,热量沿半径方向从裂缝内外边界向储热棒表面传递的路径长度相差不大;当裂缝位置特征长度>5 mm时,裂缝温差波动明显。随着放热的进行,裂缝温差均呈现先增加后下降的趋势,并且裂缝位置特征长度越大,裂纹温差增加的幅度越大,主要原因是裂缝中存在空气热阻,会阻碍混凝土连续地导热,更多的热量将改变导热路径,避开裂缝,通过混凝土沿半径方向向表面传递。裂缝内边界的导热路径较长,放热缓慢;裂缝外边界的导热路径较短,放热迅速。这会导致放热过程中裂缝温差分布差异明显。当圆心角不变时,裂缝距离储热圆棒中心越远,意味着弧状裂缝的弧长更大,由于位置和弧长的叠加效果,裂缝两侧导热的不均匀性增大,所以裂缝距离储热圆棒中心越远,裂缝温差及其增加幅度越大。与弧状裂缝相比,弦状裂缝在放热过程中的裂缝温差整体更小,是因为弦状裂缝两侧导热路径的差距比弧状裂缝的小。
3.4 裂缝参数与热应力的关系
为进一步研究裂缝参数对混凝土热应力的影响,模拟得到裂缝参数对裂缝温差峰值的影响(见图6)。由图6可得:圆心角、裂缝宽度和裂缝位置特征长度对裂缝温差峰值的影响均呈正相关性,但在不同参数条件下,弧状裂缝的裂缝温差峰值均大于弦状裂缝的裂缝温差峰值。裂缝温差对热应力有直接影响,当裂缝处的热应力超过极限会导致混凝土再次开裂,降低混凝土圆棒的热性能,并且影响其正常使用。为探究裂缝参数与裂缝温差的函数关系,进而定量分析混凝土极限热应力对应的安全裂缝参数范围,在数值模拟的基础上拟合出裂缝的圆心角、宽度和位置特征长度与裂缝温差峰值Δtmax的函数关系式。
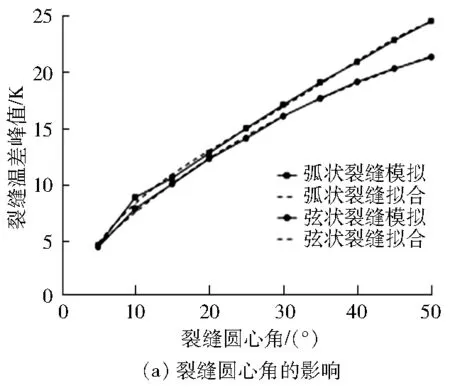
图6 不同参数对裂缝温差峰值的影响
(1)裂缝圆心角与裂缝温差峰值的关系式。
弧状裂缝Δtmax为:
Δtmax=9.9×10-5φ3-0.011φ2+
0.776φ+0.72
(3)
弦状裂缝Δtmax为:
Δtmax=4.306φ3-0.008φ2+
0.709φ+0.625
(4)
(2)裂缝宽度与裂缝温差峰值的关系式。
弧状裂缝Δtmax为:
Δtmax=2.546δ+13.818
(5)
弦状裂缝Δtmax为:
Δtmax=2.368δ+12.824
(6)
(3)裂缝位置特征长度与裂缝温差峰值的关系式。
弧状裂缝Δtmax为:
Δtmax=0.002 44x3-0.08x2+
1.797x-5.47
(7)
弦状裂缝Δtmax为:
Δtmax=0.001 77x3-0.05x2+
1.389x-4.32
(8)
所选用的混凝土的极限裂缝温差为24.105 K,通过计算得到该案例裂缝参数的安全范围(见表2)。

表2 裂缝参数的安全范围
4 结语
通过理论分析和数值模拟研究裂缝的圆心角、宽度和位置与温差的关系,并给出了温差和热应力的函数关系,定量分析了影响混凝土进一步开裂的因素,得到的主要结论为:
(1)随放热的进行,裂缝温差呈现先增大后递减的趋势,且随着裂缝的圆心角、宽度和位置特征长度的增大,变化得更剧烈。
(2)混凝土放热过程中,裂缝温差整体上与裂缝的圆心角、宽度及位置呈正相关性;但是,当裂缝位置特征长度≤5 mm时,裂缝温差基本无变化。
(3)相同裂缝参数条件下,弧状裂缝与弦状裂缝的裂缝温差的变化趋势基本一致,但弦状裂缝的裂缝温差峰值略低于弧状裂缝的裂缝温差峰值。
(4)针对该混凝土圆棒,通过公式拟合和定量分析得到:对于弧状裂缝,不开裂的要求是圆心角为0°~48.67°,宽度为0~4.04 mm,裂缝位置特征长度为0~23.43 mm;对于弦状裂缝,不开裂的要求是圆心角为0°~62.98°,宽度为0~4.76 mm,裂缝位置特征长度为0~24.29 mm。
