ALNS算法求解带软时间窗同时取送货的PCVRP问题

李 琳，陈 莹

(沈阳航空航天大学 理学院，沈阳 110136)

车辆路径问题(Vehicle Routing Problem,VRP)在物流行业有着很大的应用价值。庞燕等[1]总结了VRP的变体及其求解方法。在文献中，大多数VRP的变体问题假设配送中心具有足够数目的车辆可以满足所有客户的需求。在这类问题中，规划配送路线时，所有的客户都要被服务。但在实际生活中，存在不同客户可能存在不同的优先级和利润、每个客户不需要在特定的某天被强制访问、现有的车辆不能一次性满足所有客户的需求等情况。因此本文研究奖金收集车辆路径问题(Prize Collecting Vehicle Routing Problem,PCVRP)。PCVRP中由于实际配送条件的限制导致现有的车辆不能一次性满足所有客户的需求，只能服务部分客户。被服务的客户会给予车辆一定的奖金，被访问客户的总需求至少达到一个预定值。它的目标是使总运输成本最小化，同时使所有车辆收集到的奖金最大化。

目前对PCVRP的研究较少，对PCVRP需要进行更加深入的研究。文献[2-6]是基于带容量约束的VRP(CVRP)模型建立的PCVRP模型。其中文献[2-4]的目标函数是最小化总行驶距离和使用的车辆数目、最大化奖金收集。Long等[2]提出了一种基于Pareto的进化算法求解PCVRP。Li等[3]对建立的PCVRP模型，提出了两级自适应变邻域搜索算法，将PCVRP转化为等价的旅行商问题(TSP)，并对提出的算法进行了评价。Tang等[4]针对PCVRP问题，提出了基于循环转移的超大规模邻域迭代局部搜索算法。对100个客户的问题进行计算并验证了算法的可行性。文献[5-6]在上述基础上增加了未被服务客户对车辆的惩罚。Anurag等[5]提出了一种混合边缘重组方法求解PCVRP，基于CVRP的11个标准算例对算法进行了验证。Christos等[6]设计了分支剪切算法求解PCVRP，使用真实案例评估了有效不等式的有效性。现有文献中对PCVRP的求解侧重于启发算法，其中Li等[3]使用自适应变邻域搜索算法求解了200个客户的PCVRP问题，Tang等[4]使用大规模邻域搜索算法求解了100个客户的PCVRP问题。自适应大邻域搜索算法(Adaptive Large Neighborhood Search,ALNS)是从大邻域搜索算法(LNS)扩展而来的[7]，既满足自适应机制，也对大规模的问题有较好的求解效果。文献[8-10]分别使用ALNS对VRP的不同变体求解，结果表明ALNS求解VRP的不同变体时速度更快、结果更好。

目前的文献中PCVRP的模型基本只存在送货需求。为了更符合实际配送条件，本文在现有的PCVRP模型基础上加入了时间窗约束和同时取送货需求，建立了单目标带软时间窗同时取送货的奖金收集车辆路径问题(PCVRPTWSPD)的模型。在原有的目标函数中加入了时间窗惩罚，设计了ALNS算法对PCVRPTWSPD模型进行求解。为验证本文算法的有效性，对solomon算例[11]进行改造，构造12组不同规模的PCVRPTWSPD算例，实验结果表明ALNS在此类问题的求解时寻优能力更强。

1 模型的建立

1.1 问题描述

本文研究的模型是单目标的PCVRPTWSPD，目标函数为最小化总成本与收集到奖金间的差值。总成本包括车辆总行驶成本、车辆使用成本、时间窗惩罚。模型为单配送中心，拥有数量已知的同质型车辆，车辆的容量为C。假设车辆匀速行驶，速度为v。车辆的集合为K={1,2,…,m},∀k∈K，单位运行成本为W，每辆车的使用成本为F。客户点的集合为V={1,2,…,n}，客户总数为N。0表示配送中心。cij表示客户i和客户j之间的距离。di和gi表示客户i的送货和取货需求，pi表示车辆在客户i收取的奖金。被访问客户的总需求至少达到一个预定值Q，即至少有Q个客户被服务。本文被服务的客户以随机的方式选取。车辆从配送中心出发最终回到配送中心。eti和lti表示规定最早到达客户i的时间和最晚到达客户i的时间。ti表示车辆实际到达客户i的时间。如果tilti，车辆仍可以对客户i进行服务但需要接受相应的惩罚。f1和f2表示车辆早到的惩罚费用和晚到的惩罚费用。sti表示车辆在客户i的服务时间。

1.2 数学模型

(1)

s.t.

(2)

(3)

(4)

(5)

(6)

(7)

(8)

xijk∈{0,1};

(9)

yik∈{0,1};

(10)

式(1)为目标函数。式(2)表示车辆从配送中心出发时载货量不超过车辆的容量限制。式(3)表示预先给定的客户需求必须被满足。式(4)表示在客户点完成取送货之后车辆载重不超过车辆最大容量。式(5)和式(6)表示每个客户点最多只能被一辆车访问一次。式(7)避免出现子回路。式(8)表示车辆从客户i到达客户j的时间。式(9)和式(10)为决策变量，如果车辆k由客户i行驶到客户j，则xijk为1，否则为0；如果车辆k服务客户i，则yik为1，否则为0。

2 求解算法

本文使用ALNS对模型求解。其基本思想是输入一个初始解，根据权重选择一组destroy和repair方法对初始解进行破坏重建得到新解。判断新解的质量对新解进行评分，根据评分对destroy和repair方法的权重更新，直到满足终止条件输出最优解。

2.1 初始解

一个高质量的初始解可以提高ALNS的收敛速度，在较短的时间内得到更好的解决方案。本文使用插入法[9]构造初始解。本文建立的模型带软时间窗约束，因此在生成初始解时优先考虑行驶距离最小的客户点，允许时间窗存在偏差。其基本思想是随机选取被服务的客户，在被服务的客户集M中随机选择一个客户点v1，设L为M中未被选取的客户点集合，计算v1到L中各点的距离，选择与v1距离最小的客户点插入。如果超过车辆的最大装载(即不满足约束(2)和(4))，则将客户点插入到新的路线中。循环前面的步骤直到集合L为空。

2.2 destroy和repair方法

为增强算法的寻优能力，本算法为每组destroy和repair方法分配了权重ρ，该方法可以在较短的时间内有效地使用邻域变换方法，并提高算法的收敛速度。在迭代过程中，根据每组destroy和repair方法被分配的权重在所有方法的权重和中的占比φj，选择其中一组对当前解x进行邻域变换。φj越大，对应的这组destroy和repair方法被选到的概率越大。即ρ越大，对应的这组destroy和repair方法被选到的概率越大。每组权重占比φj的计算方法如公式(11)。参考Li等[3]的内容，根据本文模型特点设计了5组destroy和repair方法。

(11)

(1)路径内插入(inner-insertion)：随机选择一条配送路线m。删除m中的一个客户点v并插入到m的其他位置。

(2)路径间插入(outer-insertion)：随机选择两条配送路线m1和m2。在m1和m2中分别随机删除一个客户点vm1和vm2,将vm2随机插入到m1中，vm1随机插入到m2中。判断两条新路径m1_vm2和m2_vm1是否满足约束(2)和(4)。如果m1_vm2或m2_vm1不满足，则新建一条路径，将vm2或vm1插入到新的路径中。

(3)路径间交换(outer-swap)：随机选择两条配送路线m1和m2。在m1和m2中分别随机选择一个客户点vm1和vm2，交换vm1和vm2的位置。判断两条新路径m1_vm2和m2_vm1是否满足约束(2)和(4)。如果m1_vm2或m2_vm1不满足，则新建一条路径，将vm2或vm1插入到新的路径中。

(4)路径间两交换(2-outer-swap)：随机选择两条配送路线m1和m2。在m1和m2中分别随机选择两个客户点vm1-1、vm1-2和vm2-1、vm2-2，交换vm1-1、vm1-2和vm2-1、vm2-2的位置。判断两条新路径m1_vm2-12和m2_vm1-12是否满足约束(2)和(4)。如果m1_vm2-12和m2_vm1-12不满足，则新建一条路径，将vm2-1、vm2-2或vm1-1、vm1-2插入到新的路径中。

(5)路径内交换(inner-swap)：随机选择一条配送路线m，在m中随机选择两个客户点v1和v2，交换v1和v2的位置。

2.3 权重更新

在迭代过程中会对得到的新解χ′进行评分。如果χ′是全局最优解，则得分为ω1；如果χ′优于当前解x，则得分为ω2；如果χ′被接受，则得分为ω3；如果χ′被拒绝，则得分为ω4。其中ω1>ω2>ω3>ω4。令ψ=max(ω1,ω2,ω3,ω4)，则根据公式(12)对每组destroy和repair方法的权重ρj进行更新。设初始权重为ρ=(1,…,l)。本算法ω1、ω2、ω3、ω4的取值参考Ropke[7]，即ω1=1、ω2=0.4、ω3=0.25、ω4=0.1。

ρj=λρj+(1-λ)ψ,λ∈[0，1]

(12)

2.4 接受准则和终止准则

当新解χ′产生后，需要判断它是否被接受。本算法借鉴模拟退火算法的接受准则：如果χ′优于x，则接受χ′。如果χ′劣于x，则以一定的概率p接受χ′，避免算法过早陷入局部最优。p的计算方法如式(13)所示。本算法采取的终止准则是把最大迭代数作为算法停止的标准。

p=eF(x)-F(x′)/T

(13)

2.5 算法步骤

最后得到ALNS的具体步骤如下：

Step 1:通过插入法得到一个初始解x，计算x的目标函数值，令当前最优解xb=x；初始化destroy和repair方法的权重ρ=(1,…,1)；

Step 2:通过公式(11)选择一种destroy和repair方法对x进行邻域变换，得到一个新解χ′；

Step 3:判断χ′的目标函数值是否小于xb的目标函数值，如果是则xb=χ′,x=χ′，否则转下一步；

Step 4:判断χ′是否优于当前解x，如果是，更新当前解x=χ′，否则转下一步；

Step 5:判断χ′是否满足接受准则，如果满足，则x=χ′，如果不满足x=x；

Step 6:更新ρ；

Step 7: 判断是否满足停止准则，如果满足，输出最优解xb，否则转Step 2。

3 仿真实验

现有文献中对PCVRP的研究只带有送货需求，还没有对带时间窗和同时取送货PCVRP模型的研究和求解，所以目前还没有PCVRPTWSPD算例对算法进行测试，为此本文构造了12组计算PCVRPTWSPD模型的算例。选取Solomon标准算例[11]中的RC101、RC104、RC107前10、25、50和100个客户点，根据周蓉等[12]扩展 Solomon算例的方法生成配送和取货需求，其他基础数据不变。将新生成的算例命名为Rcdp101、Rcdp104和Rcdp107。对单位配送成本、车辆早到和迟到的惩罚、车辆出行成本的设置参照邓爱民等[13]的参数设置。其中配送成本为W=1元/公里，车辆早到的惩罚为f1=3元/小时，车辆迟到的惩罚为f2=6元/小时，车辆出行成本为F=20元/辆。假设至少满足的客户需求Q=0.8N，即至少80%的客户被服务，被服务的客户给予的奖金在[1,10]内随机生成，即pi=rand(1,10)。

为验证算法的有效性，本文进行了3组实验。针对不同规模的算例，本算法的迭代次数取值为：大规模(100个客户点)算例的迭代次数是400、中规模(50、25个客户点)算例的迭代次数是300、小规模(10个客户点)算例的迭代次数是100。本算法使用Python3.7编程，在CoreI7 CPU@1.80GHz 1.99GHz的笔记本上运行。

实验1选取文献[14]的求解带软时间窗同时取送货VRP的算例，使用本文算法求解。针对文献[14-16]给出的计算结果从使用车辆数(NV)和车辆行驶距离(Z)两个方面与遗传算法[15]、模拟退火算法[16]和布谷鸟算法[14]运行结果进行比较。

表1列出了本文算法运行10次获得的平均值与遗传算法[15]、模拟退火算法[16]和布谷鸟算法[14]运行结果的比较。分别使用GA、SA、MCS、ALNS表示遗传算法[15]、模拟退火算法[16]、布谷鸟算法[14]和本文算法。其中将遗传算法[15]的计算结果作为标准1，其他算法列出的结果均是与遗传算法[15]的比值。加粗部分表示本文算法与其他算法的求解结果相比，本文算法的求解结果更好。

对于本文算法，从行驶距离方面看，只有R101/10和R101/25两个算例的求解结果没有其他算法好。其中C101/25的改进最大，与GA计算结果的比值为0.63，SA和MCS与GA计算结果的比值分别为0.99、0.98。在12个算例中更新了10个算例的最优解。在算例规模超过50个客户点时，从表1中可以看到本算法的计算结果比其他算法更好。从车辆使用数量上来看，除了算例R011/10，其他全部减少。综合比较可以得出，相较于其他3种算法，ALNS在寻优求解时可避免过早陷入局部最优，在求解大规模问题时优势明显，在合理的时间内算法的求解质量更好。

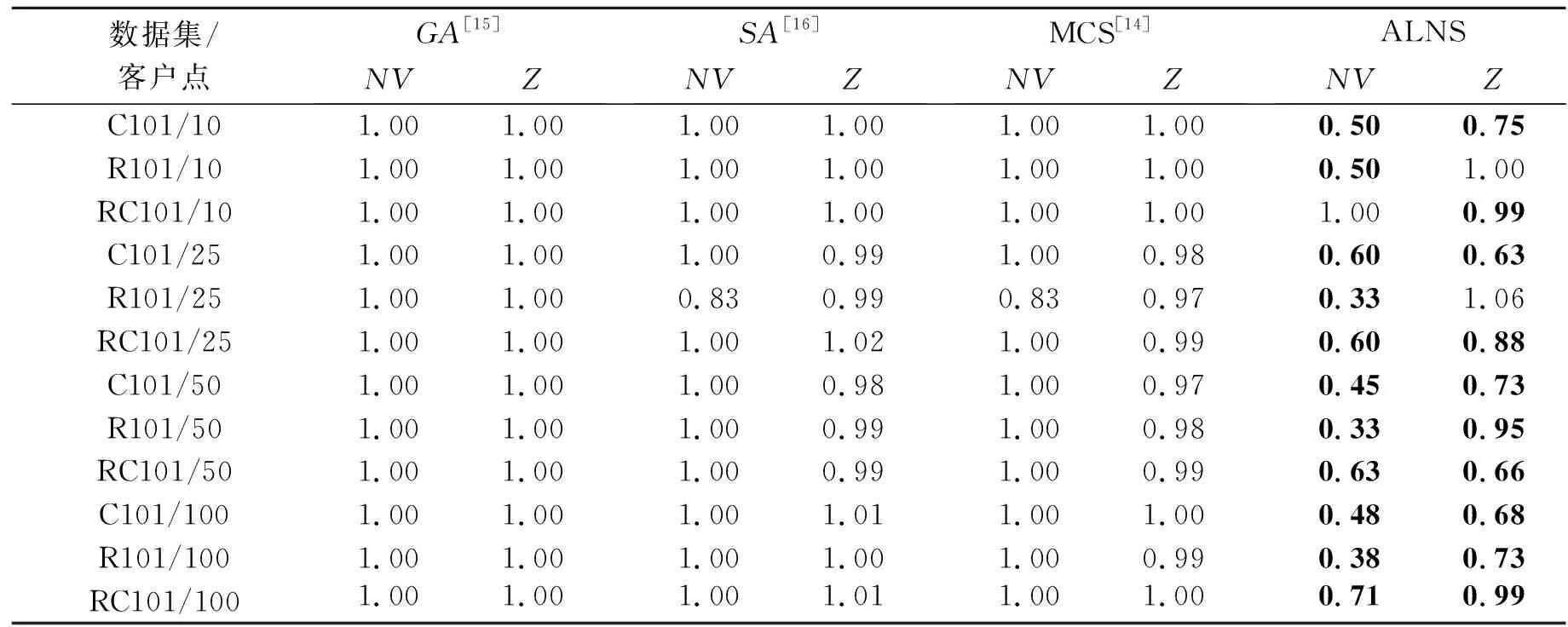
表1 ALNS与其他算法的结果对比

实验2选取本文构造的12组PCVRPTWSPD算例。使用本文提出的ALNS分别对随机生成的初始解和插入法生成的初始解进行改进。

表2是使用本文的ALNS对PCVRPTWSPD算例求解10次的平均值。ALNS-random表示使用本文提出的ALNS对随机生成的初始解改进的计算结果，ALNS-insert表示使用本文提出的ALNS对提出的插入法生成的初始解改进的计算结果。COST表示目标函数值，即总成本与收集到奖金的差值。TIME表示算法的运行时间。P表示ALNS-insert计算结果与ALNS-random计算结果的比值。若比值大于1，说明ALNS-random的计算结果更好，若比值小于1，说明ALNS-insert的计算结果更好。从表2中可以得到对于两种生成初始解的方法，算法运行时间相差不多，并且运行时间较短。对于100个客户点的算例也可以在较短的时间内得到解决方案。观察P值可以得到对于PCVRPTWSPD的12组算例，使用插入法生成初始解在较短的时间内得到的解决方案更有效。随着算例规模的增加，P值逐渐减小，即ALNS-insert的计算结果比ALNS-random的计算结果有效。也就是说本文提出的插入法可以提供一个高质量的初始解来提高ALNS的收敛速度，在较短时间内得到更好的解决方案。

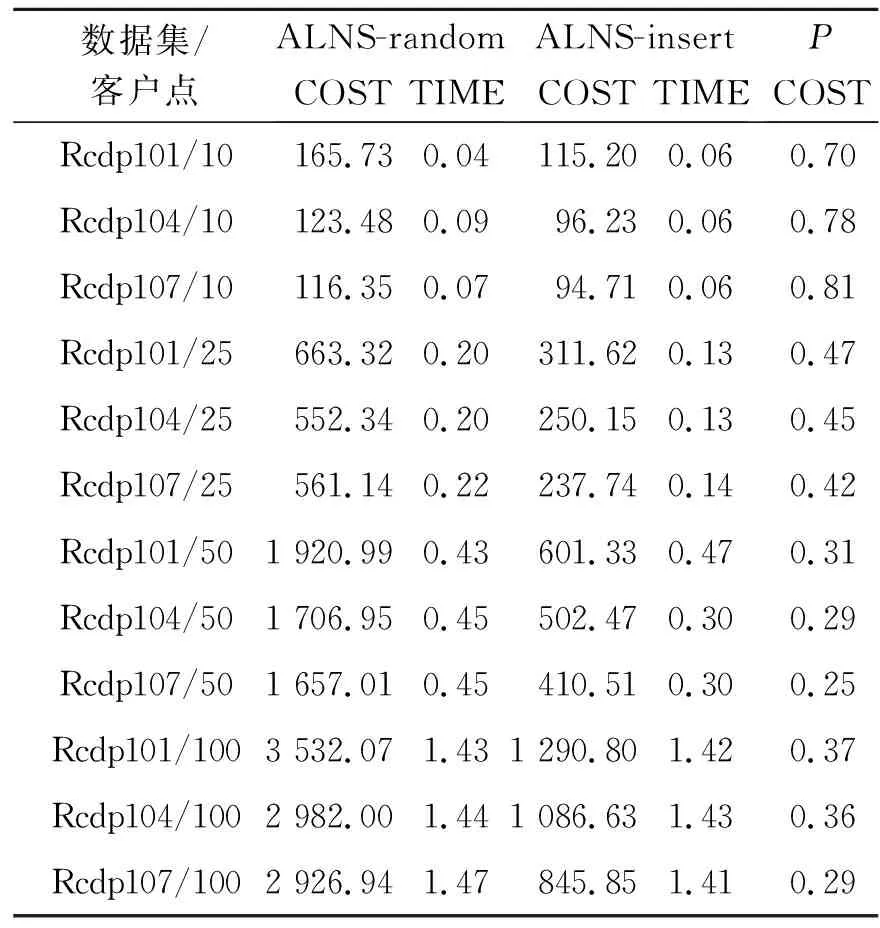
表2 ALNS改进两种方法生成的初始解

表3 PCVRPTWSPD实验计算结果比较

实验3对于本文构造的12组PCVRPTWSPD模型的算例，分别使用禁忌搜索算法、遗传算法、离散粒子群算法和本文算法进行求解。为验证本文算法的有效性，其中禁忌搜索算法、遗传算法和离散粒子群算法的初始解均根据本文的插入法生成。

表3是使用4种算法对PCVRPTWSPD算例求解10次的平均值。TS、GA、DPSO、ALNS分别表示禁忌搜索算法、遗传算法、离散粒子群算法和本文提出的自适应大邻域搜索算法的计算结果。COST表示目标函数值，即最小化的总成本与收集到奖金的差值。加粗的部分表示每个算例的最优值。最后一列BEST(COST)表示ALNS求解每个算例的最优解。从表3中可以看出，对于10个客户点的算例，本文算法的计算结果虽然不是最优值，但可以达到其他算法的求解效果。随着算例规模的增加，其余的9组算例的最优值都是通过本文算法得到的。公式(min(TS,GA,SA)-ALNS/ALNS)×100%表示本文算法对每个算例的改进程度，式中TS、GA、SA、ALNS分别表示TS、GA、SA和本文算法的计算结果。对于算例Rcdp101/25、Rcdp101/50、Rcdp101/100分别改进了6.40%、27.56%、10.18%。对于算例Rcdp104/25、Rcdp104/50、Rcdp104/100分别改进了17.93%、28.09%、5.11%。对于算例Rcdp107/25、Rcdp107/50、Rcdp107/100分别改进了19.80%、15.27%、15.61%。综合分析可知本文算法对求解大规模的PCVRPTWSPD问题更有效，得到的结果更好。

综合上述3组实验的结果，可以得到本文提出的ALNS对解决大规模的PCVRPTWSPD存在优势，得到的解决方案更有效，验证了本文算法的有效性与合理性。

4 结论

本文研究了VPR的变体PCVRP，建立了单目标的PCVRPTWSPD的模型。设计了ALNS求解模型，采用插入法生成初始解，通过自适应策略选择destroy和repair方法对解改进，并以一定概率接受没有改进的解，避免算法过早陷入局部最优。构造了12组算例并对算法进行测试。实验结果表明ALNS对大规模算例有更好的求解效果，并能在小规模问题上达到其他算法的运算效果。未来可以在本文模型的基础上对根据实时交通信息建立动态的带软时间窗同时取送货的奖金收集车辆路径问题的模型，为城市物流配送提供更好的解决方案，更好地服务企业。