吊篮钢丝绳锁扣结构强度分析和安全性评估
2021-08-03谢家学田常录王志华
谢家学,田常录,王志华
(1.雄宇重工集团股份有限公司,江苏 无锡 214125;2.江南大学机械工程学院,江苏 无锡 214122;3.无锡雄宇集团吊蓝机械制造有限公司,江苏 无锡 214125)
1 前言
经过数十年的发展,吊篮设备已广泛地应用于高层建筑物外墙的施工和维护中。由于国内厂家技术人员的不断努力,吊篮的零部件和结构整体强度、操作性能以及安全性能都获得了极大改进和提升。
目前,一种专利产品“吊篮用钢丝绳锁扣装置”得到了广泛的应用,该产品为双楔套和双开口的对称设计,见图1(a)。该产品固定在吊篮中梁上,工作钢丝绳一端通过前面楔头固定,另一端穿过前梁端滚轮悬吊篮体;安全绳一端通过后方楔头固定,另一端穿过前梁端滚轮与安全锁连接固定。该产品不再需要固定钢丝绳的绳夹和相关固定螺栓等复杂零件,而是随钢丝绳拉力增加而自行锁死。该产品不仅极大地提升了吊篮安装和拆卸的工作效率,同时提高了吊篮操作的安全性,已获得广泛的应用和好评。最近,又有一些类似产品出现,其结构略有变化,典型的见图1(b)。鉴于该产品目前的大量应用情况,本文试对其进行结构强度分析和安全性能评估。
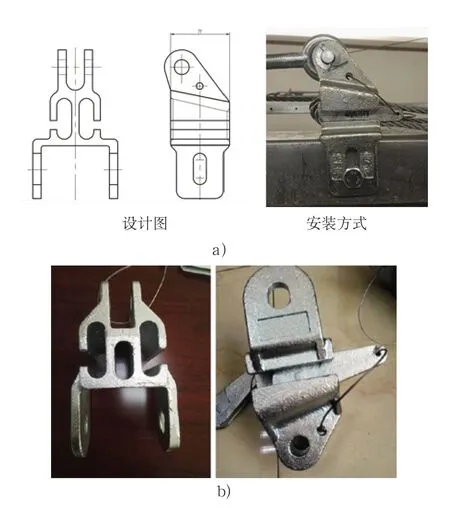
图1 吊篮用钢丝绳锁扣装置和工作安装方式
2 楔套受力分析
楔套受力如图2 所示。当楔头受力拉紧时,楔头和钢丝绳可看作一个整体相对于楔套向图示下方移动,P1,P2为楔头和钢丝绳作用于楔套的正压力,F1,F2为楔头和钢丝绳作用于楔套的摩擦力,T为楔套受中梁的作用力(楔套固定在中梁上),T数值上与钢丝绳作用在楔头的力相等,二者是一对平衡力。

图2 楔套受力分析
由楔套平衡可得
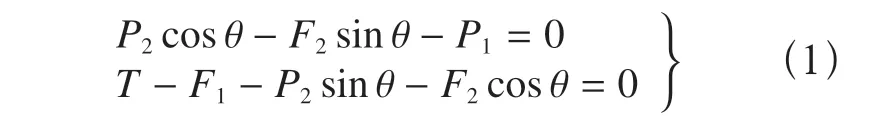
其中
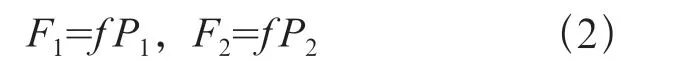
f为摩擦系数,θ为楔套倾斜一侧的倾角,解之可得
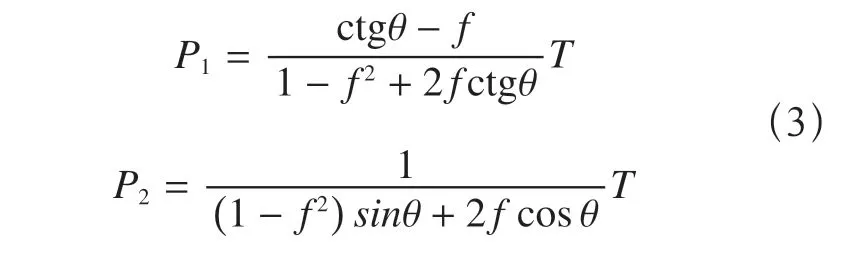
该专利产品楔套θ=13°,摩擦系数取f=0.2[1],代入数据可得楔套的受力与钢丝绳作用力T的关系

楔套受力的危险部位为内壁,根据该装置实际工作情况,下面分楔套双侧受力和单侧受力两种情形讨论。注意到P1和内壁受弯截面垂直,P2,F2为倾斜力,P2,F2在图2 所示的水平方面合力与P1是平衡力,所以计算内壁载荷只考虑P1即可。
3 楔套强度计算和实验测试
3.1 楔套双侧受力时的强度计算
该锁扣装置工作时,两个楔套内都有楔头,一个楔头受工作钢丝绳拉力,另一个楔头通过安全绳连接安全锁固定。所以工作时只有一侧楔头受工作钢丝绳作用力(篮体载荷),另一个楔头不受力。但当工作钢丝绳受力后,由于一侧楔套受力使内壁有向另一侧发生弯曲变形的趋势并夹紧另侧楔头,从而使另侧楔套也受力,此时结构实际上为双侧受力。由于一对P1是对称力,对内壁弯矩为零,内壁此时处于单向拉伸受力状态,见图3。
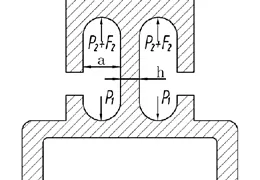
图3 楔套双侧受力情况
因而只有轴向应力,对于图1a 结构:
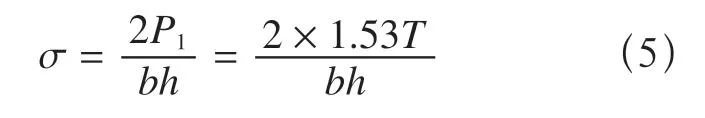
把楔套内壁厚度h=8mm 和宽度b=71mm(见图1,图3)代入,则可得到楔套内最危险部位应力随T的变化曲线,见图4。

图4 楔套双侧受力时最大应力与钢丝绳张力T之间的关系
对于标准吊篮,钢丝绳工作时张力T≈0.6t=6kN,由式(5)可计算得工作最危险部位(内壁)最大应力σ=33MPa,即图4 中方点。该产品楔套材料为35 号钢,屈服应力σs=315MPa,抗拉强度σb=530MPa,因而其工作安全系数为:

可见该产品安全系数很高,强度足够。
由图4 看到,当张力T≈5t=50kN 时,最大应力接近屈服应力σs=315MPa,此时材料接近屈服。
3.2 楔套双侧受力时实验测试
为了考察以上理论分析的结果,本文模拟该产品实际工况进行实验测试。实验在江南大学材料万能试验机上完成。图5 给出了楔套双侧受力情况下钢丝绳拉力T与试验机位移的曲线。

图5 楔套双侧受力的实验曲线
由图5 可以看出,当张力T≈4.8t=48kN 时内壁材料接近屈服,由于塑性变形较大使楔套口变大,楔头明显向外移动,试验机由于发生较大的位移而卸载(图5 右端)。此时楔套载荷已经达到设计极限值,但不会断裂破坏(抗拉强度σb=530MPa)。
3.3 楔套单侧受力情况时的强度计算
如果另侧楔套内没有楔头,此时只有一个楔套受力,内壁处于拉伸和弯曲组合载荷,受力情况见图6。

图6 楔套单侧受力情况
此时的弯矩为

抗弯模量为

最大应力发生在内壁右表面

把楔套内壁厚度h=8mm 和宽度b=71mm(见图6、图1)以及楔套孔尺寸a=18mm 代入,则可得到楔套内最危险部位应力随T变化曲线,见图7。

图7 楔套单侧受力最大应力与钢丝绳张力T之间的关系
对于标准吊篮,钢丝绳工作时张力T≈6kN,由式(8)可计算得工作最危险部位(内壁)最大应力σ=175MPa,即图7 中方点。该产品楔套材料为35 号钢,屈服应力σs=315MPa,抗拉强度σb=530MPa。因而其工作安全系数为

安全系数高于1.5。此时虽然也满足强度要求,但这种使用方法使安全系数由(6)式的9.5下降到1.5。由图7 看到,当张力T≈10kN 时,最大应力已接近屈服应力σs=315MPa,材料接近屈服,因而应该禁止采用这种安装(对侧楔套内没有楔头)方式。
3.4 楔套单侧受力实验测试
本文同样对楔套单侧受力工况进行了实验测试,图8 给出了楔套单侧受力情况下楔套实验时钢丝绳拉力T与位移的关系。

图8 楔套单侧受力的实验曲线
当张力T≈35kN 时内壁材料明显屈服,由于塑性变形较大使楔套口明显向一侧弯曲,受力一侧楔套口变大楔头明显向外移动,试验机由于发生较大的位移而卸载(图8 右端)。
4 两种结构形式楔套强度计算和测试对比
以上主要分析计算了图1(a)的结构形式,下面讨论类型结构的情况。对于图1(b)结构,楔套双侧受力时,内壁此时仍然处于单向拉伸受力状态,见图9。内壁也是只有轴向应力,不同之处为有一内孔,因为是双内壁受力,应力为

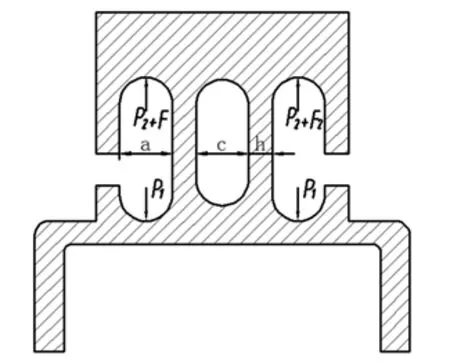
图9 楔套双侧受力情况
该楔套几何尺寸为:h=8mm,b=75mm,a=16mm,c=16mm,对于标准吊篮,钢丝绳工作时张力T≈6kN,由式(10)可计算得工作最危险部位(内壁)最大应力σ=15.3MPa。而图1(a)的结构最大应力σ=33MPa(见3.1 节),可见图1(b)结构更合理。
楔套单侧受力时,另侧楔套内没有楔头,内壁处于拉伸和弯曲组合载荷,受力情况见图10。

图10 楔套单侧受力情况
此时的弯矩为
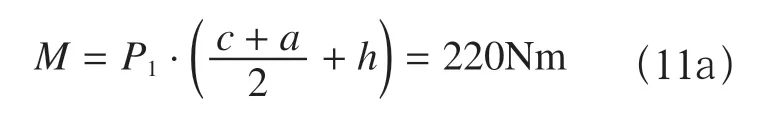
抗弯模量为

最大应力发生在内壁的右表面
而图1(a)的结构楔套单侧受力时最大应力σ=175MPa(见3.3 节),可见图1(b)结构抗弯性强度明显提高,结构更合理。
图11 给出了图1(b)结构楔套双侧受力情况下楔套实验时钢丝绳拉力T与位移的关系。

图11 楔套双侧受力的实验曲线
当张力T≈3.9t=39kN时内壁材料接近屈服,由于塑性变形较大使楔套口变大,楔头明显向外移动,试验机由于发生较大的位移而卸载。此时楔套载荷已经接近设计极限值,但不会断裂破坏(抗拉强度)。
综合以上分析可看出,无论楔套单侧或双侧受力情况下,图1(b)结构性能更好,尤其是其抗弯强度高。但图1(b)结构设计有缺陷,上方结构局部薄弱部位(外孔上部和靠近内壁处),应该补强,或者把开孔方向换为图1(a)的形式。
5 结论和讨论
由以上两种楔套理论计算和实验测试可知,标准吊篮在楔套双侧受力时,钢丝绳工作时张力T≈0.6t=6kN,图1(a)结构的内壁最大应力为σ=33MPa,图1(b)内壁最大应力σ=15.3MPa,强度足够;楔套单侧受力时,钢丝绳工作时张力T≈0.6t=6kN,图1(a)的结构内壁最大应力σ=175MPa,强度明显下降,图1(b)的结构内壁最大应力σ=27MPa,结构更合理。
以上分析的是两种极限状态,实际安装要求是双侧楔套内都有楔头,即接近楔套双侧受力的情况,但两侧力也不一定是相等的理想状态。工作时当一侧楔头受工作钢丝绳作用力,另侧楔套也必然受力,但另侧受力的大小取决于该侧楔头与安全绳固定的松紧状态,紧则力大,松则小,其数值需要根据松紧状态确定。更精确的计算需要考虑楔套和楔头变形协调条件来确定,或者考虑楔头、钢丝绳和楔套之间相互摩擦、接触做三维有限元分析。
根据以上理论分析和实验测试情况看出,现场工况非常接近楔套双侧受力相等的状况。也就是说,对于标准吊篮,内壁强度足够。但当一侧楔套内没有楔头时,即楔套单侧受力时,图1(b)结构的内壁强度仍然够,但图1(a)内壁最大应力偏大,建议现场禁止使用这种(一侧楔套内没有楔头)安装方式。
