基于支持向量机的气压辅助掘进条件下盾构隧道地表变形预测研究

李方毅，张晓平, *，许 丹，姜 军，周 智，沈 婕，王浩杰，张心悦

(1. 武汉大学土木建筑工程学院，湖北 武汉 430072； 2. 中铁十一局集团有限公司，湖北 武汉 430061； 3. 中铁建华南建设有限公司，广东 广州 511458； 4. 广州地铁集团有限公司，广东 广州 510330)

0 引言

全断面机械化盾构隧道施工方法以掘进速度快、机械化程度高、安全性能好、对环境影响小等显著优点逐渐成为城市地铁隧道施工的主流方法。采用盾构法进行地铁隧道施工过程中，难免会对周围地层产生扰动，进而诱发地表变形。当变形超过一定限度时，极易对隧道、周边建(构)筑物以及地下浅埋管线等造成不同程度的损伤破坏，诱发工程安全事故。因此，在盾构隧道施工过程中，选择合适的方法合理预测地表变形，进而提前采取加固措施，对有效防止过大地表变形造成重大工程安全事故显得尤为必要。

众多学者采用经验公式法[1-2]、理论分析法[3-4]、数值模拟法[5-6]等多种方法对盾构掘进诱发地表变形进行了研究。但经验公式法缺乏理论基础，无法将不同工况与经验公式联系起来； 而理论分析法和数值模拟法无法考虑现场工程地质条件和人工作业环境的高度复杂性，在计算参数选取方面存在固有缺陷。近年来，以人工智能为代表的盾构掘进诱发地表变形预测模型，以其在有效捕捉地表变形量与相关影响因子之间非线性关系方面的显著优势，已经逐渐成为预测盾构掘进诱发地表变形的有效手段[7]。孙钧等[8]使用人工神经网络对隧道开挖引起的地表沉降进行预测，论证了该方法的可行性和适用性。Suwansawat等[9]考虑隧道几何因素、地质因素、盾构运行因素等影响因素，使用人工神经网络成功预测最终变形量。田执祥等[10]认为人工神经网络在样本有限时预测精度不高，提出了基于支持向量机(SVM)的隧道变形预测方法。

支持向量机与人工神经网络相比，有效克服了神经网络易陷入局部最小值而非全局最小值的固有缺陷[11]。但目前支持向量机的超参数(如惩罚参数c和核函数参数g)选择大多通过反复试验获得，试错过程复杂，且难以保证得到最优结果。潘宇平等[12]使用交叉验证法获取了支持向量机超参数组合，但存在耗时过长等不足。Zhang等[13]使用粒子群算法优化支持向量机超参数，并对比分析了多种预测方法性能，但其研究中所使用的训练数据与预测数据均为随机选取，难以指导盾构隧道工程现场施工。袁志明[14]使用粒子群算法优化支持向量机超参数，预测了地铁基坑开挖导致的变形。俞俊平等[15]则使用PSO-SVM模型预测了边坡变形。但目前尚未有针对气压辅助掘进条件下的盾构隧道地表变形预测模型。

本文引入粒子群算法(PSO)对支持向量机(SVM)超参数进行优化，建立PSO-SVM预测模型。针对气压辅助掘进工法特点，考虑上覆黏土层厚度，优化输入参数，并改进上覆非均质土层模型参数计算方法。以广州地铁18号线陇枕出入场线为例，采用已掘进区间隧道地表变形数据对PSO-SVM模型进行训练，进而对未掘进区间隧道地表变形进行预测，并将预测结果与PSO-BP模型和SVM模型预测结果进行对比分析，以期为后续气压辅助掘进条件下的盾构隧道变形预测提供理论依据和技术支撑。

1 PSO-SVM预测模型

1.1 支持向量机原理

支持向量机是根据广义超平面理论，把样本点从低维空间映射到高维空间，在高维空间内进行线性回归，进而得到在原低维空间的非线性回归方法[16]。支持向量机目标为找到一个偏差为ε的函数fsv(x)。

(1)

式中：φ为权值矢量；x为输入矢量；i为矢量个数，i=1,2,…,n(n为输入个数)；xi∈Rn为对应输出值；yi∈R；K为核函数；b为阈值；ε为偏差。

支持向量机常用的核函数有多项式核函数、径向基核函数和sigmoid核函数等，本文采用径向基核函数，如式(2)所示。

(2)

式中σ为径向基核函数的宽带。

1.2 粒子群算法

粒子群算法(PSO)是一种受鸟类捕食行为启发所开发的算法[17]，算法首先初始化粒子群位置向量和速度向量，利用初始位置向量计算初始适应度值，然后通过迭代更新粒子位置与速度向量找到最佳适应度值。粒子速度和位置更新公式如式(3)和式(4)所示：

(3)

(4)

式(3)—(4)中：i表示第i个粒子；k为迭代次数；Xi为位置向量；Vi为速度向量；c1和c2为非负的常数，称之为加速度因子；r1和r2为分布在[0,1]之间的随机数；ω为惯性权重；Pt为单个粒子的个体最优极值；Pg为所有粒子的全局最优极值。

1.3 PSO-SVM预测模型

本文引入粒子群(PSO)算法来优化支持向量机(SVM)模型惩罚参数c和核函数参数g，使用这2个参数值代替粒子群算法中的位置向量。更新粒子群并通过适应度函数计算适应度值，迭代之后输出最优适应度值，以该适应度值下的参数组合作为SVM的参数来构建最优模型。

(5)

式中：n为每个子集中的样本数；ai为实测值；f(bi)为模型预测值；j表示第j个子集；k为子集个数。

2 模型输入参数优化

2.1 气压辅助掘进工法

在土压平衡盾构掘进中，若上覆土层气密性较好，为提高掘进效率，控制地表变形，可采用气压辅助掘进工法，即在保持盾构土舱压力恒定的前提条件下，通过土舱顶部的注入孔向土舱内注入压缩空气，使得土舱上部内形成稳压的气室，通过气压和土压共同作用来平衡隧道掌子面水土压力，如图1所示。在实际掘进过程中，碴土界面大约保持在土舱高度1/2处。

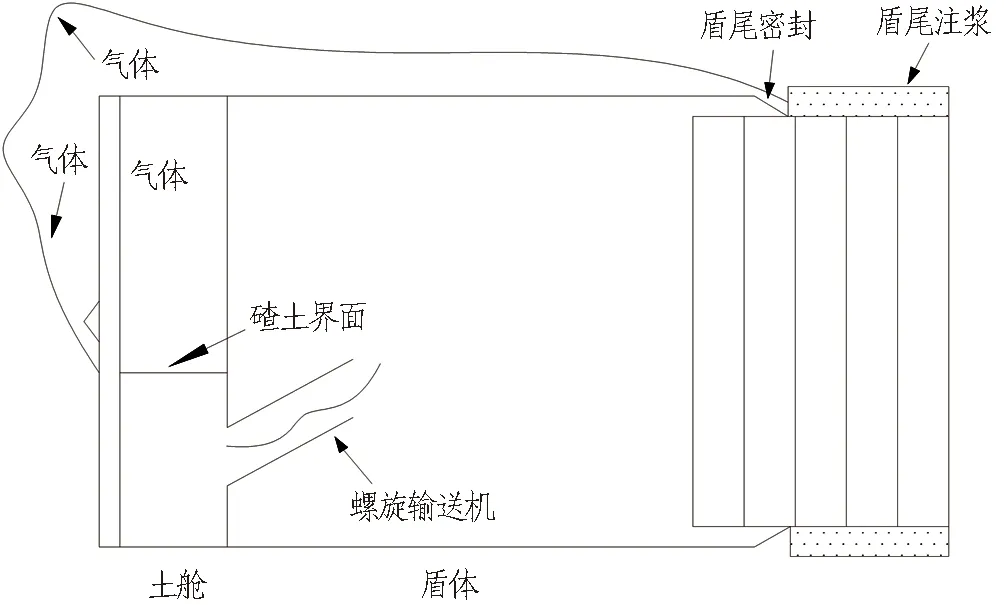
图1 气压辅助掘进工法示意图

气压辅助掘进主要有以下优点： 1)气压作用于掌子面，可以防止掌子面前方及上部地下水进入舱内，减少地下水流失，防止喷涌，有利于控制地表变形； 2)由于舱内碴土量少，气压减磨效果显著，可以充分减小刀盘转矩，减小总推力，降低刀具磨损； 3)可以有效防止刀盘结泥饼，保证掘进效率； 4)由图1可知，气压还会作用于盾尾同步注浆处，压实浆液，提高注浆质量。

但目前气压辅助掘进主要存在2个问题： 1)地层气密性对气压保持影响较大。目前认为该方法适用于上覆土层为粉砂质、黏土等气密性较好的土层，在砂砾、砂质等气密性较差的地层中保气效果较差。气密性较好的土层厚度也会影响气压稳定效果，若黏土层厚度较薄，气压可能击穿保气层，土舱从而与外部空间形成通道，地表出现漏气情况，产生较大变形，严重时可能会导致无法保压，致使地表发生塌陷[18]。因而在预测气压辅助掘进条件下盾构掘进引起的地表变形时需考虑上覆黏土层情况，而现有一般模型并未考虑该因素。2)气压辅助掘进下地表变形更为复杂。由于土舱上部为气压，气压取值一般为土舱某一点位处静水压力值，因而掌子面上部总存在气压大于水土压力的超压区。田勇坚等[19]提到，气压辅助掘进条件下，盾构切口到达时地表就会产生隆起。另外，广州地铁18号线陇枕出入场线采用气压辅助工法施工区间段3个隧道轴线上方测点变形曲线如图2所示，3个测点都在盾体通过时产生10 mm左右隆起变形，这说明带压气体会充填盾体与土体之间的空隙，不仅在刀盘切口到达之前，而且在盾体通过时也会导致地表产生隆起，这与纯土压掘进时的变形曲线不同[20]。

气压辅助掘进条件下，黏土层厚度、气压大小与变形关系密切，之前预测模型并未考虑这些因素对于地表变形的影响，因而需要优化之前模型的输入参数以提高工程适用性。

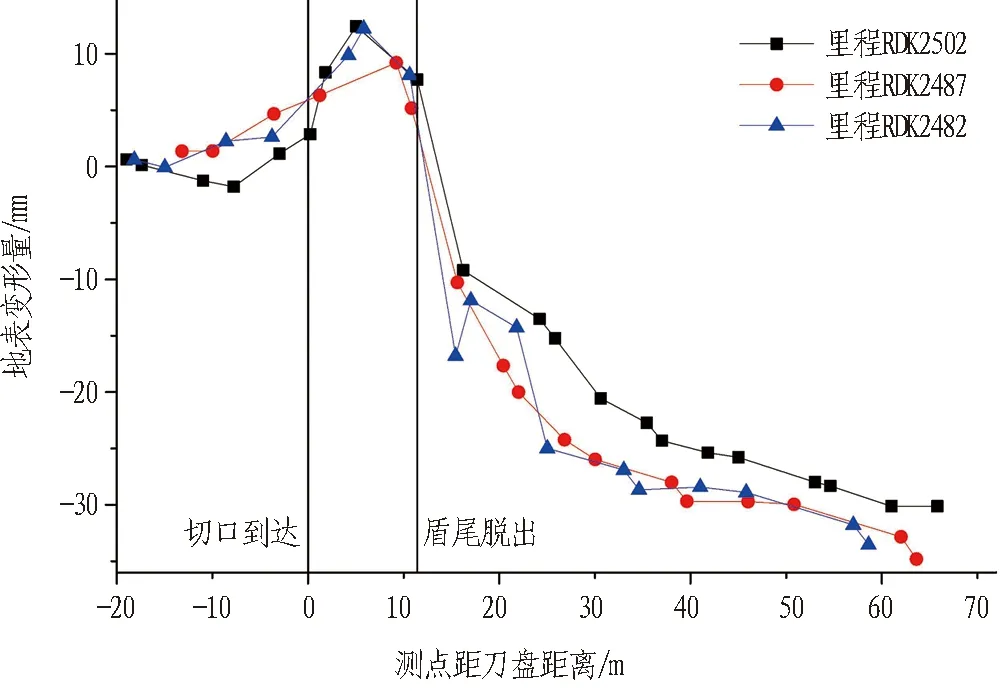
图2 气压辅助掘进条件下隧道轴线测点纵向变形曲线

2.2 模型输入参数优化

针对气压辅助掘进工法特点，优化PSO-SVM预测模型的输入参数。

1)隧道几何参数。隧道埋深与断面直径对地表变形影响较大，同一工程中断面直径为定值，因此选取隧道埋深H与断面直径D的比值H/D作为几何因素输入参数。

2)工程地质参数。如2.1节所述，黏土层是气压辅助掘进过程中的保气层，其厚度对于地表变形量有很大影响，之前预测模型中并未考虑该参数，因此在本文引入上覆黏土层厚度h这一参数作为预测模型的输入参数。

考虑上覆非均质土层物理力学性能会对地表变形产生较大影响，因此根据土层厚度对上覆土层标贯次数加权平均值N′、上覆土层黏聚力加权平均值c′、上覆土层压缩模量加权平均值E′ 3个参数进行处理，详细计算方法如下。

(6)

式中：n为土层种类总数；hi为第i层土层厚度；h为上覆土总厚度。

3)盾构施工参数。之前预测模型以土舱压力作为输入，并未考虑气压大小，而在气压辅助掘进条件下，气压对于变形的影响不可忽视，因而在本文模型中增加土舱上部气压这个输入参数。考虑到作用于掌子面前方及盾体上部土体的气压不仅在刀盘到达之前，而且在盾体通过地表测点时都会对测点变形量产生影响，因此取刀盘到达测点前至盾体通过测点时共10环气压平均值作为土舱上部气压Ap取值。

施工参数选取土舱上部气压Ap、同步注浆压力Gp、同步注浆量Gv、总推力F作为输入参数。

3 工程应用

3.1 工程概况

广州地铁18号线陇枕出入场线RDK2+703～RDK1+809自RDK2+703里程处一次始发，沿市南路自东向西前行364 m后接收，明挖186 m后自RDK2+153里程处盾构二次始发，继续沿市南路掘进。为合理控制地表变形，提高盾构掘进效率，广州地铁18号线陇枕出入场线自RDK2+522里程起采用气压辅助掘进工法。

隧道采用土压平衡盾构施工，盾体长12.88 m，开挖直径8.78 m，管片外径8.5 m，内径7.7 m，环宽1.6 m。隧道上覆土层自上而下分别为杂填土、淤泥质土、淤泥质粉细砂、粉质黏土、全风化泥质粉砂岩、强风化泥质粉砂岩、中风化泥质粉砂岩。详细地质剖面图和地层主要物理力学参数分别如图3和表1所示。

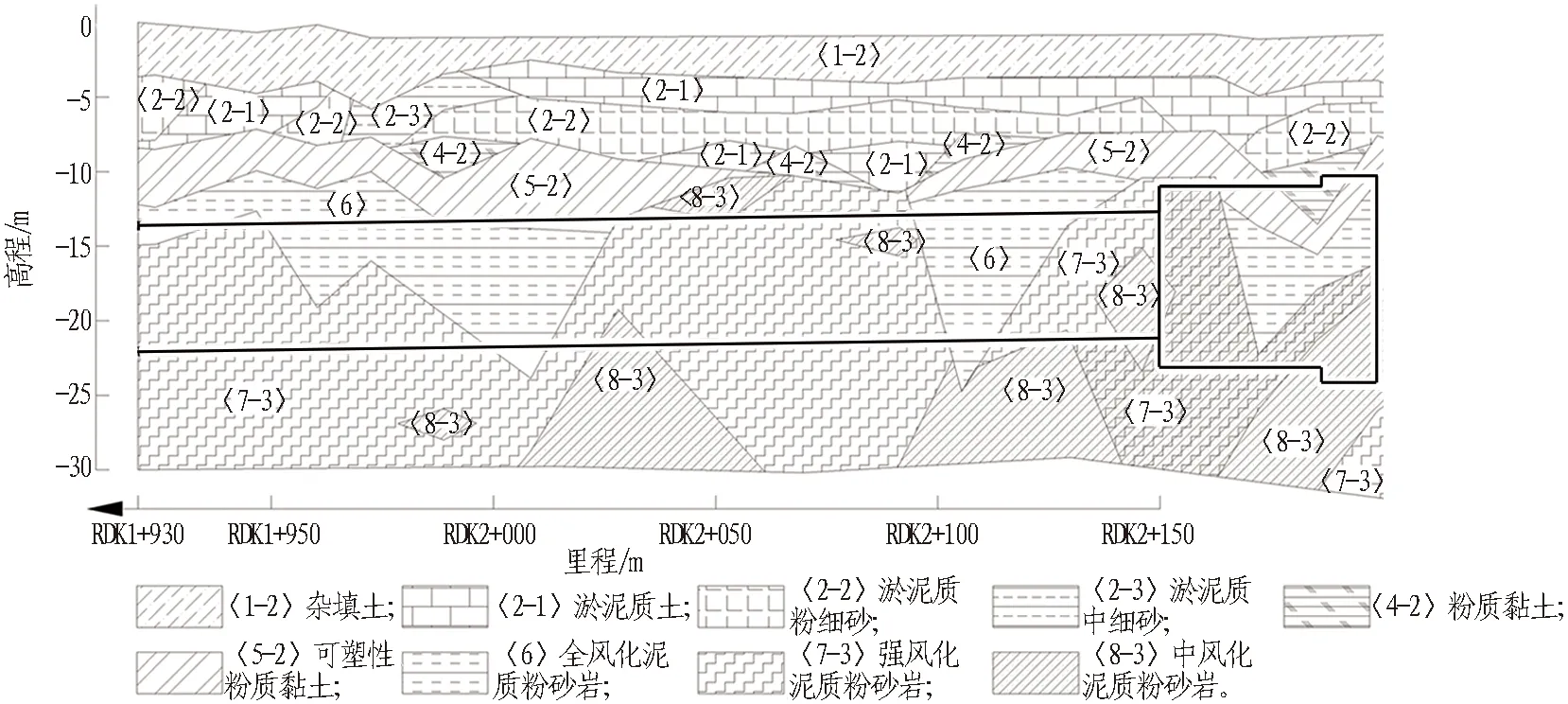
图3 地质剖面图

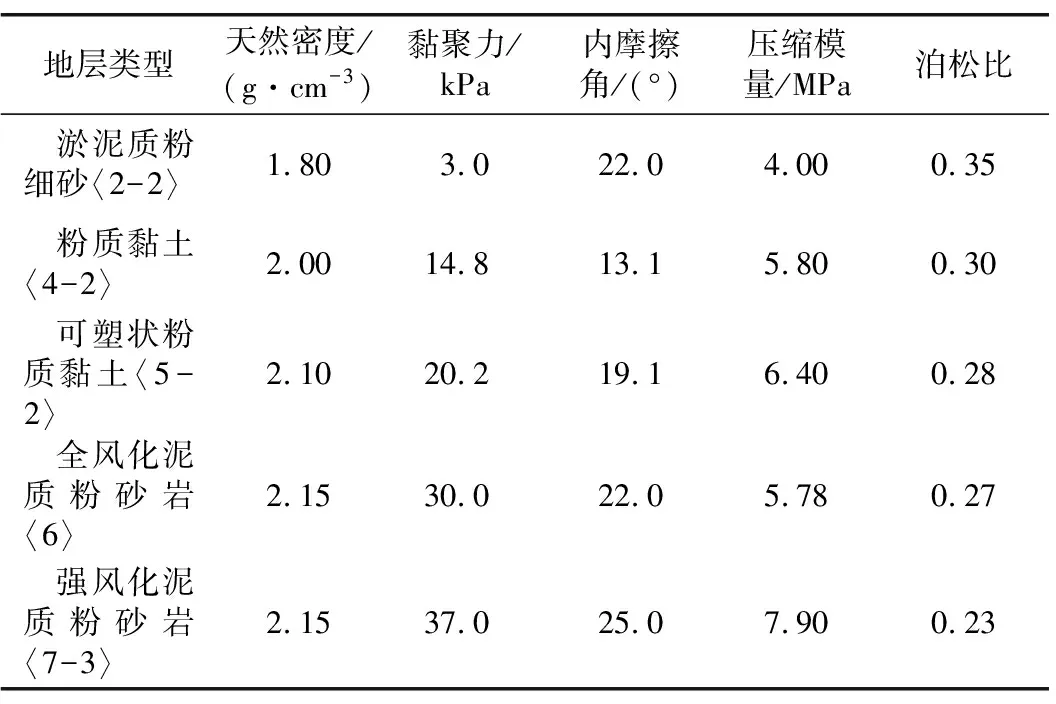
表1 地层主要物理力学性能参数

PSO-SVM预测模型数据为陇枕出入场线RDK2+522～RDK1+809段隧道轴线上方测点地表变形数据，该段采用气压辅助掘进工法，数据共计40组，其中，RDK2+522～RDK1+874段32组数据作为训练集构建PSO-SVM预测模型，RDK1+859～+809共8组数据作为预测集。本工程中输入参数上覆黏土层厚度h取为粉质黏土〈4-2〉和可塑状粉质黏土〈5-2〉厚度之和。原始输入参数分布范围如表2所示。为消除输入参数不同数量级对模型预测性能的影响，所有数据在训练预测前统一进行归一化处理。

(7)

式中：xmax为输入参数最大值；xmin为输入参数最小值。

表2 输入变量和输出变量的分布范围

3.2 超参数优化结果

使用粒子群算法优化支持向量机惩罚参数c和核函数参数g，2个超参数搜索区间均为0.001～10。经多次试验后，粒子群算法初始参数确定为： 粒子群规模为50，最大迭代次数为100，学习因子c1=c2=1.5，速度Vmax=-Vmin=0.5。为在前期进行全局搜索，后期进行局部搜索，惯性权重设置为线性递减，表达式如式(8)所示。

(8)

式中：ωmax和ωmin分别为初始和最终惯性权重值，取值分别为0.9和0.4；i为当前迭代次数；T为最大迭代次数，取值为100。

将广州地铁18号线陇枕出入场线RDK2+522～RDK1+809段隧道轴线上方测点地表变形数据前80%，即前32组，用于PSO-SVM模型的超参数确定。k折交叉验证法中的k取为4，将32组数据分为4份，每份8组地表变形监测数据，每次3份训练、1份测试。

为分析该混合算法的可行性，对每一次迭代后的最小适应度值进行统计追踪，结果如图4所示。当迭代次数超过60次之后，适应度值达到相对稳定状态。因此，本研究最终选取最小适应度值对应的惩罚参数c和核函数参数g值，即c=1.94,g=0.97。

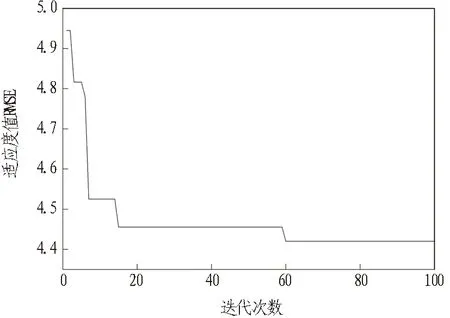
图4 模型适应度值进化曲线

3.3 模型预测结果

为了验证PSO-SVM预测模型的可靠性，取训练集数据(即前32组地表变形数据)对PSO-SVM模型进行训练，训练完成之后再次将训练集数据输入到PSO-SVM模型中，评估训练效果。若训练效果符合要求，则将预测集数据(即后8组地表变形数据)输入到训练完成的模型中进行预测。训练集、预测集的预测结果如图5所示。

训练集中的隧道地表变形量分布范围较广，实测值与预测值的绝对误差都较小，平均绝对误差MAE=0.51 mm。该结果说明PSO-SVM模型较好地捕捉到前32组地表变形数据与影响因子间的内在规律，以此为基础，将预测集(即后8组地表变形数据)参数输入到模型中，对前方开挖区间地表变形进行预测分析，结果表明： 预测值和实测值的平均绝对误差MAE=1.31 mm。

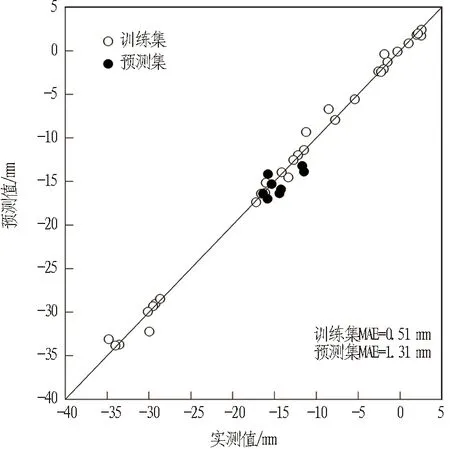
图5 训练集与预测集分布图

建立PSO-BP模型、SVM模型与PSO-SVM模型进行对比分析，该3种模型均针对气压辅助掘进工法优化了输入参数。对于模型超参数，PSO-BP模型为粒子群算法优化BP神经网络结构，最终确定1层隐含层和13个隐含层节点的结构； SVM模型参考Chen等[21]研究中的超参数取值，惩罚参数c=5.65和核函数参数g=0.06。各点预测结果如图6所示。3种模型预测效果对比如表3所示。由表3可知，较之于PSO-BP模型和SVM模型，PSO-SVM模型具有更高的地表变形预测精度。虽然PSO-BP模型个别点预测误差比PSO-SVM模型更小，但从预测值与实测值的均方根误差来看，PSO-SVM模型仅为1.54，而PSO-BP模型和SVM模型分别为6.39和4.20，由此看出PSO-SVM模型表现出更好的预测稳定性。

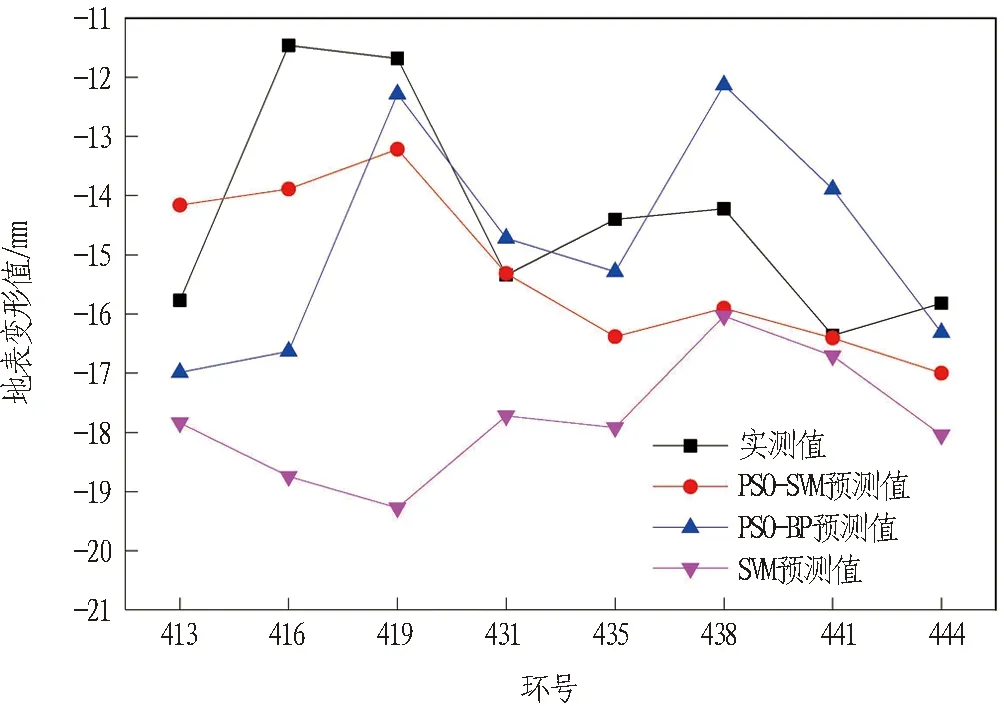
受地表环境影响，在419—431环未设置监测点。

图6 PSO-SVM、PSO-BP、SVM模型预测值与实测值比较

Fig. 6 Comparison of measured values and values predicted by PSO-SVM, PSO-BP, and SVM models

表3 3种模型预测结果对比

4 结论与讨论

1)本文引入支持向量机(SVM)理论，利用粒子群算法(PSO)对支持向量机的超参数组合进行优化，以交叉验证集的均方根误差平均值作为粒子群算法的适应度函数，获得了支持向量机最佳超参数组合，提升了模型的预测精度。

2)根据气压辅助掘进下地表变形特征，合理引入上覆黏土层厚度和土舱上部气压表征土层气密性和气舱压力对隧道地表变形的影响，针对上覆非均质土层改进模型参数计算方法，对PSO-SVM模型输入参数进行优化，使用该模型对广州地铁18号线陇枕出入场线某使用气压辅助掘进工法的盾构区间进行预测，结果表明该模型预测平均绝对误差为1.31 mm，可以较好满足工程实际需要。

3)基于平均绝对误差、最大绝对误差和均方根误差的对比分析，优化超参数后的PSO-SVM模型预测效果精度和稳定性整体优于PSO-BP模型和传统SVM模型，PSO-SVM模型表现出更为优越的工程适用性。

本研究优化了PSO-SVM模型的输入参数，虽在一定程度上考虑了气压辅助掘进工法对变形的影响，但气压影响与地层条件关联密切，对于地质参数的输入仍需进一步精细化研究。此外，本文模型对于该工程地表变形具有一定的预测精度，但数据样本来自同一工程，由于现场工况的复杂性，应尽量收集其他类似工程下实测数据，进一步提高该模型的适用性。同时，下一步可开发适用于该工法的动态与实时地表变形预测模型，以便更好地指导工程施工。