基于AFC数据的城市轨道交通限流优化模型研究

任秋阳

（北京交通大学，北京100044）

城市轨道交通作为城市公共交通的重要组成部分，不仅大大缓解了城市地面交通压力，而且对于促进生态保护有着突出的贡献。当前，我国的轨道交通业迎来了高速发展时期，很多一线城市都已经开通了地铁，并且，地铁网络的覆盖面积越来越广泛，极大地方便了人民群众的出行。但是近年来随着城市的人口数量急剧上升，城市轨道交通的运营出现了一系列如运营里程上升但线网密度较低、列车应对干扰能力较低进而影响乘客出行等问题，现今从管理层面提高运输效率已经成为轨道交通领域研究的重要内容。通过研究基于AFC数据的城市轨道交通限流优化模型可以有效缓解城市轨道交通出现的客流量分布极不均衡的现状，提高轨道交通的出行效率，进而对城市轨道交通的运输效率有所促进。王兴蓉等人[1]对客流需求不确定下城市轨道交通线路协同限流问题展开分析，降低了不确定需求对限流策略的扰动，但却增加了部分情境下的滞留人数。赵锴[2]与黄倩[3]两人均对单条线路的客流优化模型进行了研究，但均基于客流状态稳定，客流需求稳定的假设分析，使得在面对不确定因素时模型灵敏度较低。张正等人[4]分析了在大客流的背景下如何实现车站间协同限流的方法，采用流量平衡原理描述客流分布动态关系，但并未考虑车站客流OD结构的变化。李凌燕[5]分析了大客流在城市轨道交通路网上的传播与疏散，通过建立SIRS大客流路网传播模型讨论了应对大客流冲击的控制策略，但在相关分析中基于客流需求确定假设弱化了动态分析的过程。

本文基于AFC数据与以往高峰数据进行分析相比，对于客流需求有着更加精确的描述，考虑到了车站OD结构的变化，使模型在处理客流需求不确定时有着较好的灵敏度。同时模型基于多目标优化的思想，充分考虑城市轨道交通运输能力、客流需求两个因素。

1 城市轨道交通限流优化模型

1.1 问题描述

基于北京市地铁AFC数据，建立数学模型，首先可以实现在识别乘客路径基础上，描述客流量的时间变化以及客流结构的OD变化。在此基础上，需要结合城市轨道交通运输能力、客流需求等因素，建立模型分析最佳客流量的取值范围。

最后以城市轨道交通单一线路为例，建立目标函数。在考虑客流的动态变化的基础上，分析如何使得乘客滞留时间最小化、广义乘客出行时间最小化，最终实现同时考虑地铁系统与乘客需求的最优。

1.2 模型假设

所提出的模型基于以下假设：

（1）对于进站口到达乘客仅有限流与进入两种选择，不存在主观放弃城市轨道交通出行方式这一行为。

（2）乘客到站后以尽快登入列车为优先，不考虑乘客主观上选择滞留。

（3）不考虑站内布局与收费安检对进站客流量走行时间的影响，即乘客在限流结束后进入站台可即时到达车站站台。

（4）在列车运行时段内，列车的发车时间间隔严格执行计划时刻表，并认为列车准点率保持较高水平。

（5）换乘客流视作本线客流，换出客流为出站客流，换入客流为进站客流。

1.3 模型构建

基于上述符号，城市轨道交通限流优化模型优化问题（O）可构建为如下的多目标数学优化模型：其中关于目标函数的说明：

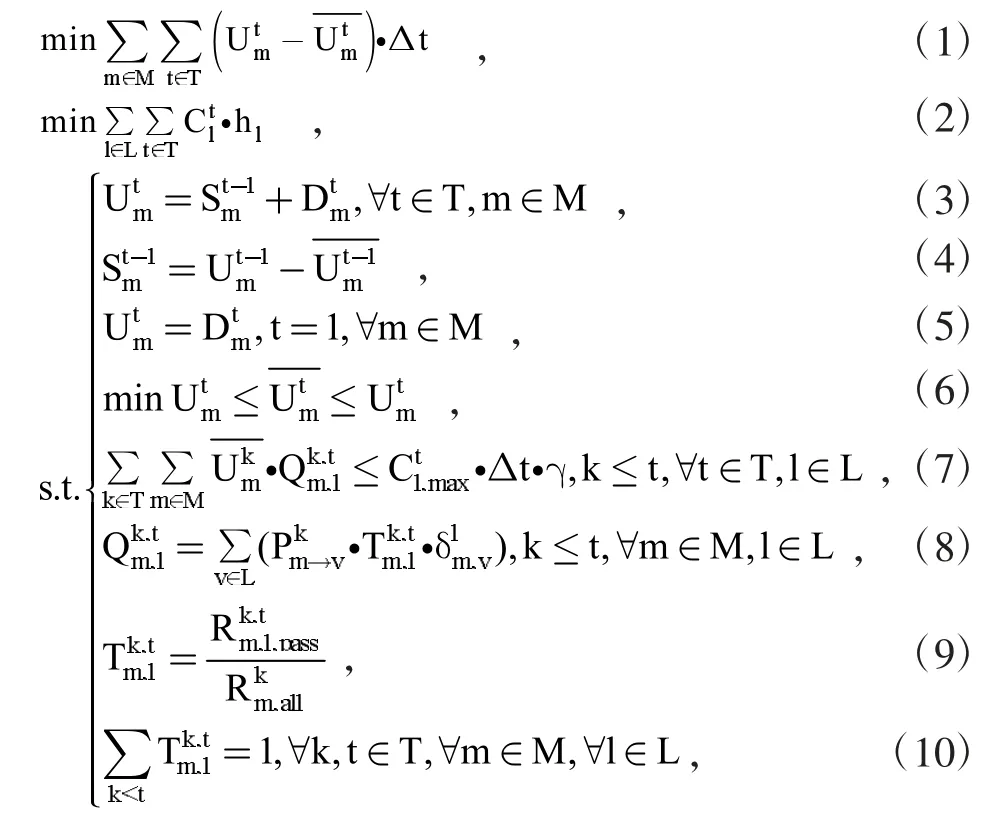
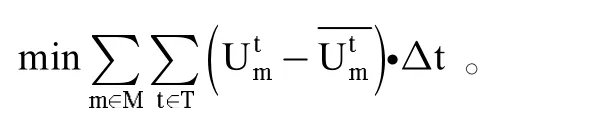
式（2）为广义乘客出行时间最小的目标函数；乘客出行时间正比于乘客旅行距离。因此，从乘客个体角度考虑，若要使整体乘客出行时间最小，我们可以等效于乘客旅行距离最小来表示。从宏观角度来看，一列车内的所有乘客在某一个区间内的旅行距离是相同的，因此，我们可以用每一区间客运周转量C与该区间距离h的积来表示所有乘客的旅行距离之和，进而确定目标函数为：

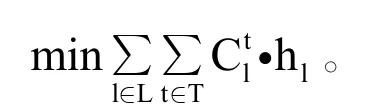
关于约束函数的说明：式（3）表明在某一限流时间段t内，实际进站客流由这一时间段内新到达的客流和前一时间段内滞留的客流两部分组成。式（4）表示前一时间段内滞留的客流可用上一阶段实际进站客流量与上一时间段最佳进站客流量之差决定。式（5）描述考虑到第一个时间段的客流需求量无法用上一时间段的滞留客流量表示，因此直接用该时间段内到达乘客数表示。式（6）表示最佳进站客流量必须小于实际进站需求，且在不采取封站措施的情况下，应该满足大于最小实际进站客流量这一条件。式（7）中，通过客流传播系数来表示区间在时间段t内的通过客流量，并以区间在时间段t内的输送能力作为约束。式（8）中，客流传播系数可体现客流对区间输送能力占用情况，同时该占用情况与列车运行状况以及客流OD结构以及区间是否在OD内三个因素相关，所以可通过式（8）将四者联系。式（9）与式（10）表示了在时段k内通过车站m的列车数目在时段t内通过区间l的数目的比例，各比例之和为1。

2 算例分析

2.1 求解环境与案例概述

为解决该优化问题，我们决定使用模拟退火来寻找该模型的最优解。先取定优化变量的初始值，得到目标函数对应的值。优化变量会随着迭代次数增加而变化，从而得到新的目标函数值。当目标函数更加优秀时，对应的优化变量将会有更大出现的可能。最终经过若干次迭代之后，我们会获得一个稳定的目标函数值，最后求出与之相对的优化变量从而得到该模型的最优解。

本节构造以北京市八通线某日切实算例，测试所提出模型和算法的求解效果和效率。自适应性大规模邻域搜索算法由MATLAB8.0编程，其中，各计算参数设置为默认值。所有计算在CPU为Intel Core i7－10875H 2.30 GHz、RAM为16.00GB、操作系统为Windows 10－64Bits的个人电脑上执行通过。

2.2 求解结果分析

从求解结果中可以看出∶双桥、土桥两站是限流效果最好的两个车站。基于以下几点原因：（1）双桥、土桥是乘客进站需求量最大的两个站；（2）通过单个车站限流模型的求解，双桥、土桥两个站分别是限流效果最好的两个站；（3）通过限流站数为2的限流模型的求解，同时对双桥、土桥进行限流，对于八通线来说限流效果最好；（4）土桥作为始发站，承载较大客流，会影响后续车站客流的进入。

八通线限流前后指标对比如表1所示。

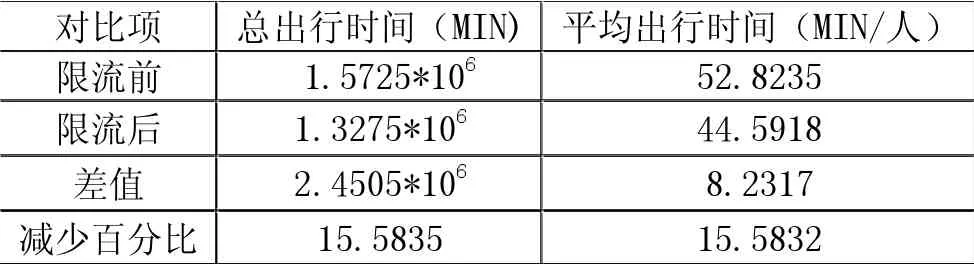
表1 八通线限流前后指标对比

3 限流措施分析

3.1 动态限流方案

我们可以发现，动态限流方案的限流效果要明显优于固定的限流方案。而动态限流方案的核心在于如何选择控制时间段的长度。从问题的求解效果来看，限流时段的长度越小，限流的效果越好。但在实际生产运营中，很难做到实时限流，需要投入大量的资金和技术。因此，基于北京地铁的运用状况，根据2.2节结果显示的求解取30分钟是最为合适的。

3.2 限流车站与时段的选择

从求解结果中，我们不难发现随着限流车站数的增多，虽然站内拥挤度得以极大缓解，列车内的拥挤度也相应地变小。但是，过多的限流车站会导致乘客总体滞留时间的增长。因此，在制定选择滞留车站的决策时，需要综合考量站内、列车的拥挤程度和乘客总体的出行效率两个方面。此外，每一条线路都会出现明显的高峰现象。虽然本模型所采用数据只有早高峰的，但我们也不能忽视晚高峰的存在。因此，限流时段的选择必须基于早晚高峰的具体时间。由2.2节给出的求解结果，早高峰的限流时间最好为7：00AM-10：00AM。此外，由于通勤线站点距离市中心距离的不同，出现高峰点的时间段也会随着距离市中心距离的变近而稍往后延缓，因此采用错峰限流是一种更为合理且有效的措施。

3.3 限流强度

每一条线路的每一个车站限流强度都不一样。由于限流强度的计算是通过最佳进站客流量和实际客流需求确定的。在列车运行图确定的情况下，最佳进站客流量的变化范围并不大。如果不出现演唱会等特殊活动的情况下，每日的实际客流需求变化不会非常大，因此车站管理人员可以相应地参考前一天的限流强度，并根据实际的客流情况做适当修改。

4 结论

本文的研究以城市轨道交通大客流聚集问题为背景，依托于AFC数据与多目标规划的思想，以八通线为例，进行了城市轨道交通单线高峰限流优化。构建了基于车站-线路的客流传播系数，将列车运行状况以及OD变化联系起来，以便反映客流数量的时空变化与客流OD结构变化过程。在此基础上构造了使乘客滞留时间最小化、广义出行时间最小化的目标函数，结合约束函数，使得模型在一定程度上可以有效缓解出现大规模人群聚集的频率。在模型的建立中，通过引入车站-线路的客流传播系数，反映客流OD结构变化过程，在此基础上进行动态限流，使得模型具有更好的限流效果。但本文并未考虑列车运输组织对单线多目标优化方案制定的影响且将换进客流视作进站客流，换出客流视作出站客流，未考虑到换乘客流的到达规律。因此，在未来应当从单线限流优化拓展到多线限流优化方案，结合旅客画像充分考虑换乘客流的特点并加入至模型，以期提出更具有普遍意义的多目标优化方案。