基于最优控制理论的航空飞行安全性以及经济性的优化研究

王 威

（中国国际航空股份有限公司，北京101318）

1 最优控制理论

简单来讲，这一理论属于现代控制理论的某个分支，主要用来研究如何让控制系统的性能标准达到最优化的基础条件和综合方法。例如，提出一个最优的控制方法，让空间飞行器从某个轨道转移到另一轨道中，且消耗燃烧最少；选择某种规律下的温度调节方式和所需原料配比情况，让化工反应期间获取最多的产量；提出最科学的人口政策，促使人口发展期间的劳动力、中老化及抚养等指数都可以达到最优化。这些都属于基于最优控制理论研究的经典问题。要想解决上述问题，需要为受控运动工程构建相应的运动方程，并为控制变量设定明确的取值范围，了解运动的初始状态与目标状态，而后为这一运动提出一个可以评价品质性能的标准。

2 性能数据及质心运动

通过研究飞机所受外力作用下飞机质心运动的变化规律，就能明确飞机的飞行性能。因此，要想了解影响飞机性能的各项问题，首先要掌握飞机所受外力和相应的质心运动方程。其中，大气环境、气动力及其力矩、发动机等都是常见的外力作用。

第一，大气环境。由于地球的大气环境非常复杂，如果按照温度随高度变化的形式来划分，那么其包含对流层、平流层、中间层、电离层、散逸层五个层次，而对流层和平流层是最适宜飞机飞行的环境，但所处层次的温度、密度和压强等存在较大差异。以国家标准大气为例，研究飞机飞行性能时，可以利用ICAO标准来仿真设计真实大气层环境，此时需要根据飞行高度来计算大气层的压力、密度及温度等。此时，环境的静温比TAR和静压比PAR与高度会满足以下关系式：

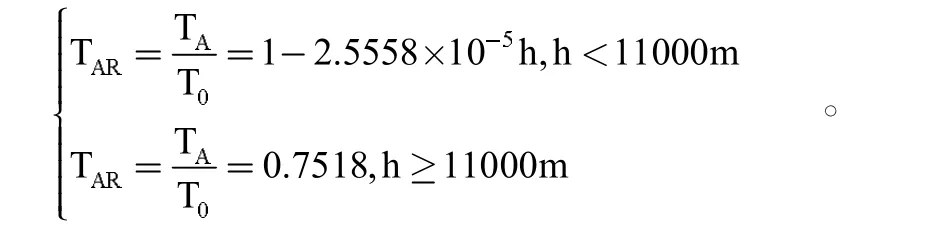
第二，气动力及其力矩。对飞机运行而言，其拥有的气动特性直接影响着飞机的整体性能，因此研究其气动力也是工作的重点和难点。通过利用气动曲线和插值算法得到其中包含的升力、阻力和侧力三项系数，实际计算方法如下：

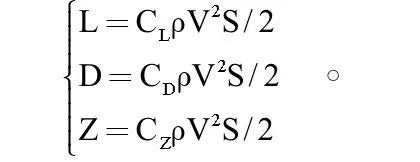
第三，发动机。以涡轮风扇发动机为例，其是由压气机、风扇及涡轮等部件构成的。由于其具备两条气流通道，因此最终进入气道的气流将会分为两股，其一将从外壳和内壳进入外函道，并由风扇实施增压，其二将进入内涵道，与普通涡轮喷气发动机类似。在这一过程中，发动机形成的推力就是内外构成的推力之和，具体公式为：

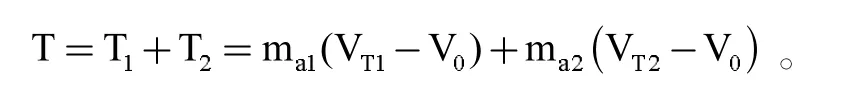
第四，运动方程。通过描述飞机内外距力和运动参数间的关联，并利用相关坐标系进行公式推导，最终能为研究航空飞行性能提供有效的数据依据。一方面，动力学方程。假设将飞机看作是刚体，那么按照理论力学分析可知，飞机在空气当中进行的一般运动包含了质心运动与绕质心进行转动。此时，结合牛顿第二定律可以得到如下方程；另一方面，运动学方程。要想掌控飞机的运行轨迹，不仅要了解外力和运动参数间的关联，而且要研究质心位置随着时间改变的规律。通过对飞行速度V进行分解，最终可以得到如下所示的方程关系式：

3 飞机性能计算及航迹优化分析

飞机每次运行前后都需要按照规定要求执行各项任务，如滑行、离地、巡航、着陆等，而要想研究它的性能，需要对飞机运行所有相关任务的速度、高度及特性等进行全面分析。本文主要重点研究以下问题：

第一，起飞。从松开刹车开始飞机离开地面，一直到上升到1500ft高度后，这一期间叫做飞机起飞的全过程。一般来讲，起飞场道时期是指飞机从地面开始加速滑行一直到离地面超过35ft后。同时，速度将会≥安全速度V2，且飞机从35ft的高度继续上升的过程叫做起飞航道阶段。

第二，爬升与下降。本文研究的爬升是指从飞行航迹的终点开始，也就是离开机场地面1500ft的高度开始。而在飞机达到终点以前，它要从巡航高度降低到与机场地面相距1500ft的区域，并准备开始着陆，这就是飞机的下降。这两个过程都属于飞机运行期间的过渡阶段，计算公式分别为：

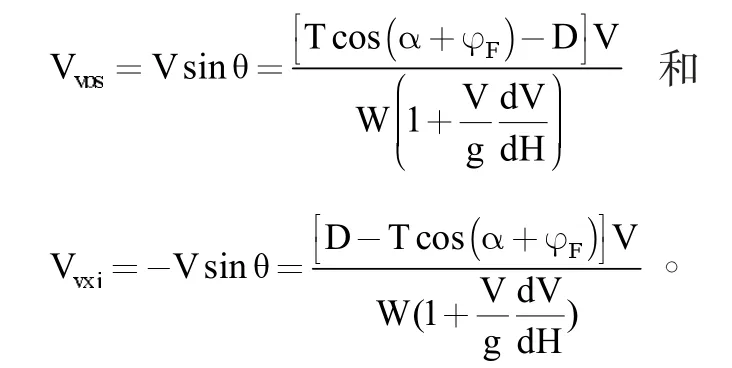
第三，巡航。这一性能是指飞机可以长久运行的能力，其主要涉及到航程与航时两点内容。一般来讲，民航飞机需要按照巡航期间经过的水平距离、所需时间及消耗燃油等指标进行性能计算。由于在这一过程中，飞机需要保持直线飞行，高度和速度是不会发生变化的，所以可以用以下公式计算巡航期间的航程与航时。

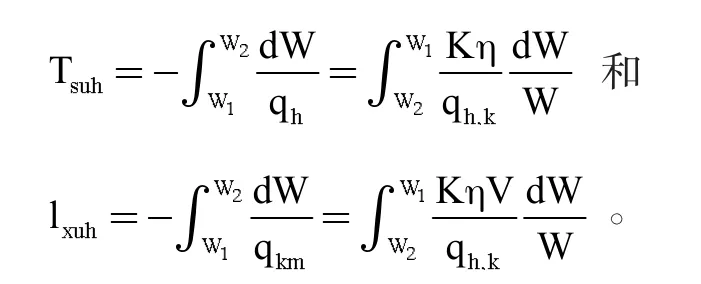
4 利用粒子群优化算法分析飞行成本最优轨迹

4.1 提出问题

在民航事业飞速发展中，随着空中飞行数量的增加，航空公司要想在获取效益的同时控制成本支出，必须要研究飞行所需燃油和时间。

4.2 构建模型

本文研究主要从爬升、巡航和下降三方面入手进行最优轨迹的分析。为了优化飞机整体运行成本，可以基于实际应用成本来评估飞机的经济性能。换句话说，可以结合燃油成本和时间成本构建完善的综合性指标，为现阶段最常见的性能分析方法有：第一，推力法；第二，功率法；第三，能量高度法；第四，解析法。

结合上文得到的运动方程优化飞机的爬升、巡航和下降这三点性能，最终可以得到如下所示的质点运动方程：

而按照最优控制理论分析，明确哈密顿函数，也可以得到这三者的最优化飞行条件：

4.3 算法

现阶段，处理最优化问题的算法很多，如遗传算法、蚁群算法等，但本文主要利用粒子群算法进行求解。假设选取总群大小N=40，进化代数=100，学习因子c1=c2=2，搜索空间维数W=1，惯性权重（w）为0.7298，精度（eps）为0.00001，那么具体计算步骤如下所示：第一，随机初始状态下的种群个数，就能得到粒子群算法当中粒子所在的位置和运行速度；第二，研究种群当中每个粒子群的适应度。通过计算目标函数的最小值，就能得到粒子适应度的相应函数为fitness（V，W）=-λx；第三，结合适应度函数计算它所在位置为pbesti（t）=（xi1，xi2，...，xin），

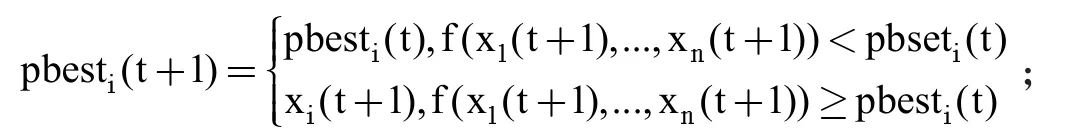
第四，明确全局最优位置为

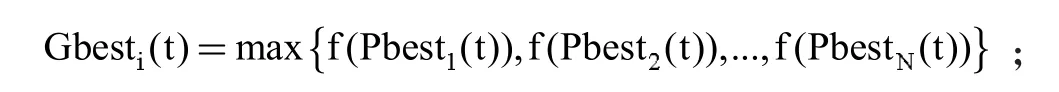
第五，优化种群个数的公式为

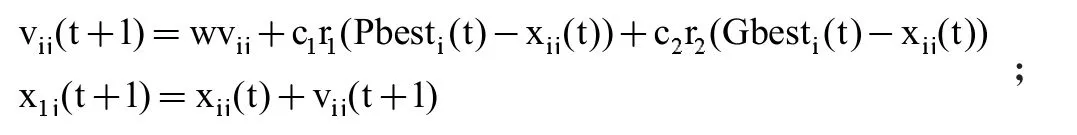
第六，分析结束条件，假设符合条件就可以停止计算，不然需要再次转移到第二步进行计算。

4.4 仿真结果

利用MATLAB实施仿真设计，对比分析最终结果与省油飞行轨迹，具体如表1所示。由此可知，成本最优的飞行轨迹当中的速度会不断提升，虽然减少了消耗的时间，但增加了消耗的油量。假设可以选择更加适宜的成本指数，将能有效控制成本支出。

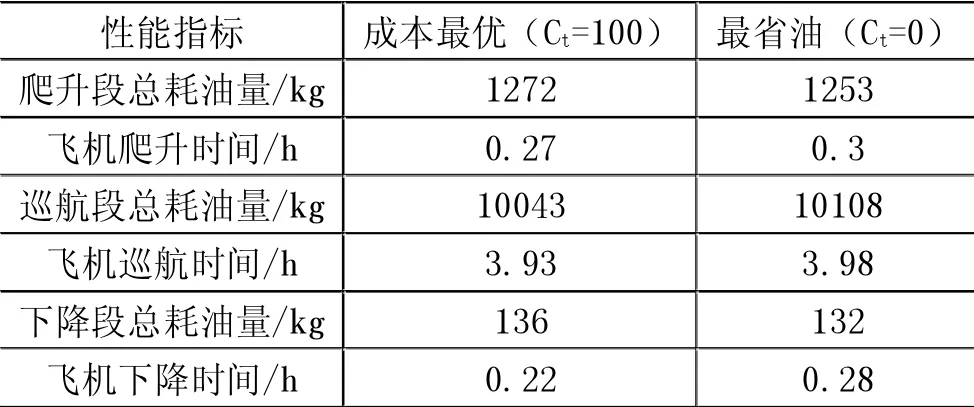
表1 成本最优与省油性能的指数对比分析表

5 结束语

综上所述，面对民航领域飞速发展为航空公司带来的全新挑战，如何在保障发展效益的同时控制飞行成本支出，并保障空中交通安全，已经成为全社会关注的焦点。因此，本文在了解最优控制理论的基础上，通过全面研究与飞行计算有关的性能数据，分析飞机运行的质心运动方程，并由此入手开发相应的计算系统软件，能保障实践研究可以得到准确的飞机性能数据。同时，在分析最优轨迹时，还考虑了时间和耗油的成本支出，并由此构建了目标函数，得到了飞机飞行状态下的优化方程，而后依据MATLAB软件和粒子群算法实施计算，得到了明确的优化方式。需要注意的是，与航空飞行的安全和经济有关的研究较为复杂，上文研究并不全面，其中遗漏或存在缺陷的地方也是未来继续探讨的重难点。