高层结构整体稳定性探析——以马尾物联网1#楼为例

陈克用

(福建众合开发建筑设计院有限公司 福建福州 350004)

0 引言

在建筑结构分析中的竖向荷载的侧移效应，当结构发生水平位移时，竖向荷载就会出现垂直于变形后的竖向轴线分量，这个分量将增大水平位移量，同时也会增大相应的内力，即P—△二阶效应。设计者可根据需要选择是否考虑其对结构的不利影响。

建筑结构整体稳定分析主要是考虑P-Δ效应，其相应的控制指标是刚重比。结构的侧向刚度和重力荷载之比简称刚重比。刚重比必须满足规定的数值，否则结构将在风荷载或水平地震作用下，由于重力荷载产生的二阶效应过大从而引起结构的失稳甚至倒塌。《高层建筑混凝土结构技术规程》规定(以下简称《高规》)，当结构的刚重比数值满足最低限值要求时，结构的整体稳定具有适宜的安全储备，但应考虑结构的重力二阶效应的不利影响。当结构的刚重比数值足够大时，结构的重力二阶效应已经很小，可以不计其不利影响。

1 公式推导

《高层建筑混凝土结构技术规程》(JGJ3-2010)，以下简称《高规》[1]要求。

或

规范对EJd的规定前提为结构弹性等效侧向刚度，是按倒三角分布荷载作用下顶点位移相等的原则，将结构侧向刚度折算为竖向悬臂构件受弯等效侧向刚度而得出的。实际建筑工程中，作用力是作用在杆件中间各个点，以各楼层为一质量集中作用点。这样，以全楼总高度为杆件长度，各楼层标高处为各个力作用点，力学简图如图1所示。

图1 力学简图模型

在图1荷载分布下，采用挠曲线微分方程，来解其相应得临界应力，得出如下结果：

(1)

上式是适用于所有不同楼层质量，不同楼层高度的建筑结构。

而《高规》的公式5.4.1-1：

是基于体型和荷载分布均匀假设[2]并通过上式(1)简化得到的，假设前提条件如下：

(a)各楼层层高相等

(b)各楼层质量相等

G1=G2……=Gi

在上述两个假定条件下，带入(1)式，则(1)式变换为如式(2):

(2)

根据数列求和公式，上式继续变换为如式(3)：

(3)

当n趋于无穷大时，上式变换为如式(4)：

(4)

根据规范《高规》(JGJ3-2010)第5.4节及相应条文说明可知：控制结构P-Δ效应确保结构稳定安全，就是要控制结构考虑P-Δ效应后位移值Δ*与未考虑P-Δ效应时位移值Δ的比值不超过10%，如式(5)和式(6)：

(5)

△*/△≤1.1

(6)

再根据式(4)代入(5)式，并结合(6)式子推导可得：

(7)

式(7)公式与《高规》5-4.4-1相比，可以说与规范公式基本一致[4-5]。

如果控制结构位移足够小并能不考虑结构结构虑P-Δ效应的限值，即按弹性分析的二阶效应对结构内力、位移增量控制在5%左右，根据规范《高规》5.4.1条相应条文说明，即将式(6)公式右侧1.1改为1.05时，如下式：

△*/△≤1.05

(8)

这时，根据(4)(5)(8)式子推导可得：

(9)

2 工程概况、结构体系

该工程建于福州市马尾快安，工程建设所在地抗震烈度为7度，地震分组为第三组，场地土类别为Ⅲ类,50年重现期风荷载为0.7 kPa，地面粗糙度为B类，结构安全等级为二级。设计使用年限为50年。

该工程结构高度为98.1 m，共26层，采用框架核心筒结构，框架抗震等级为二级、剪力墙抗震等级为二级，其底层因建筑功能需求，二层局部挑空跃层结构平面如图2所示，标准层结构平面如图3所示。

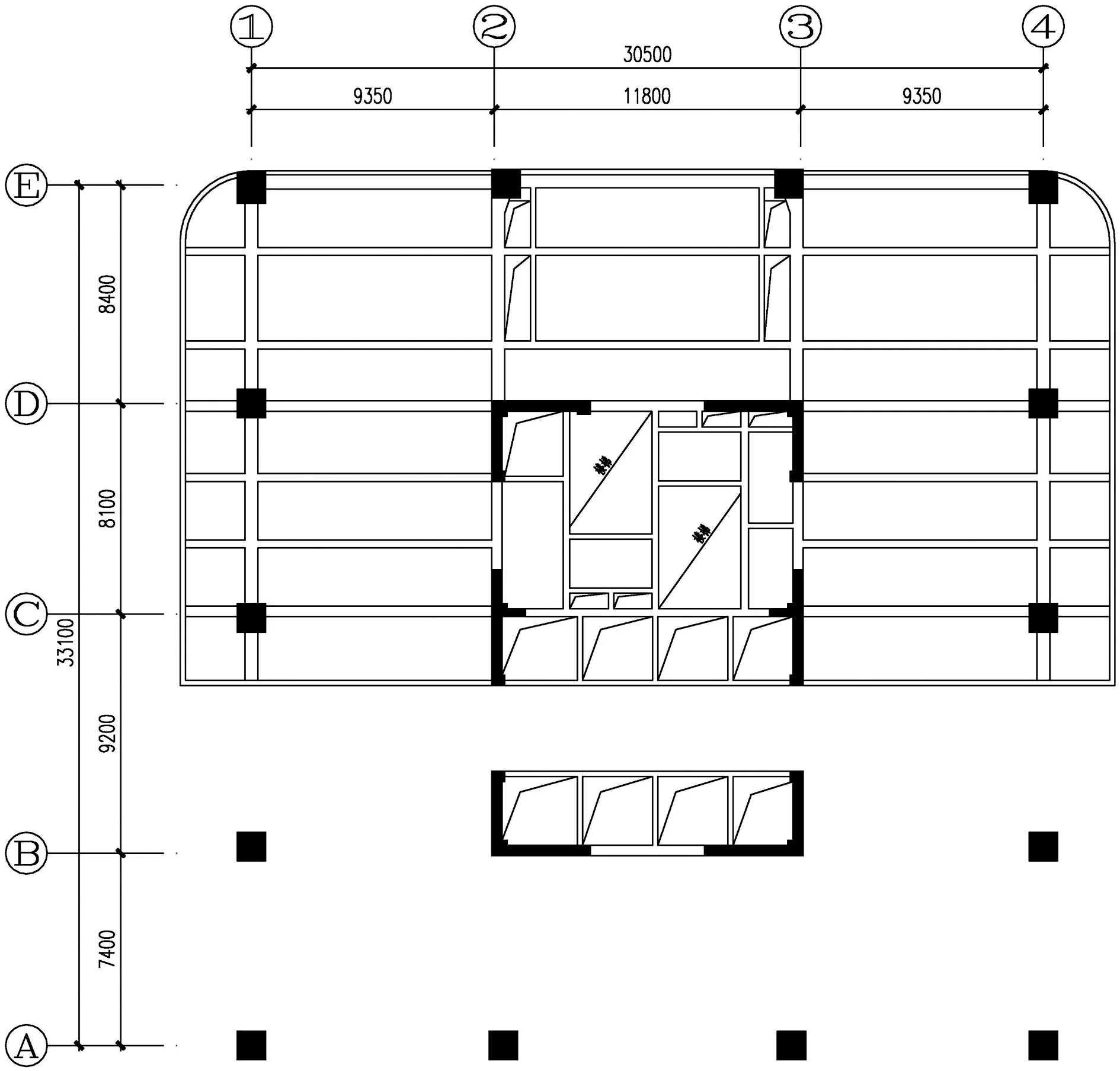
图2 二层结构平面

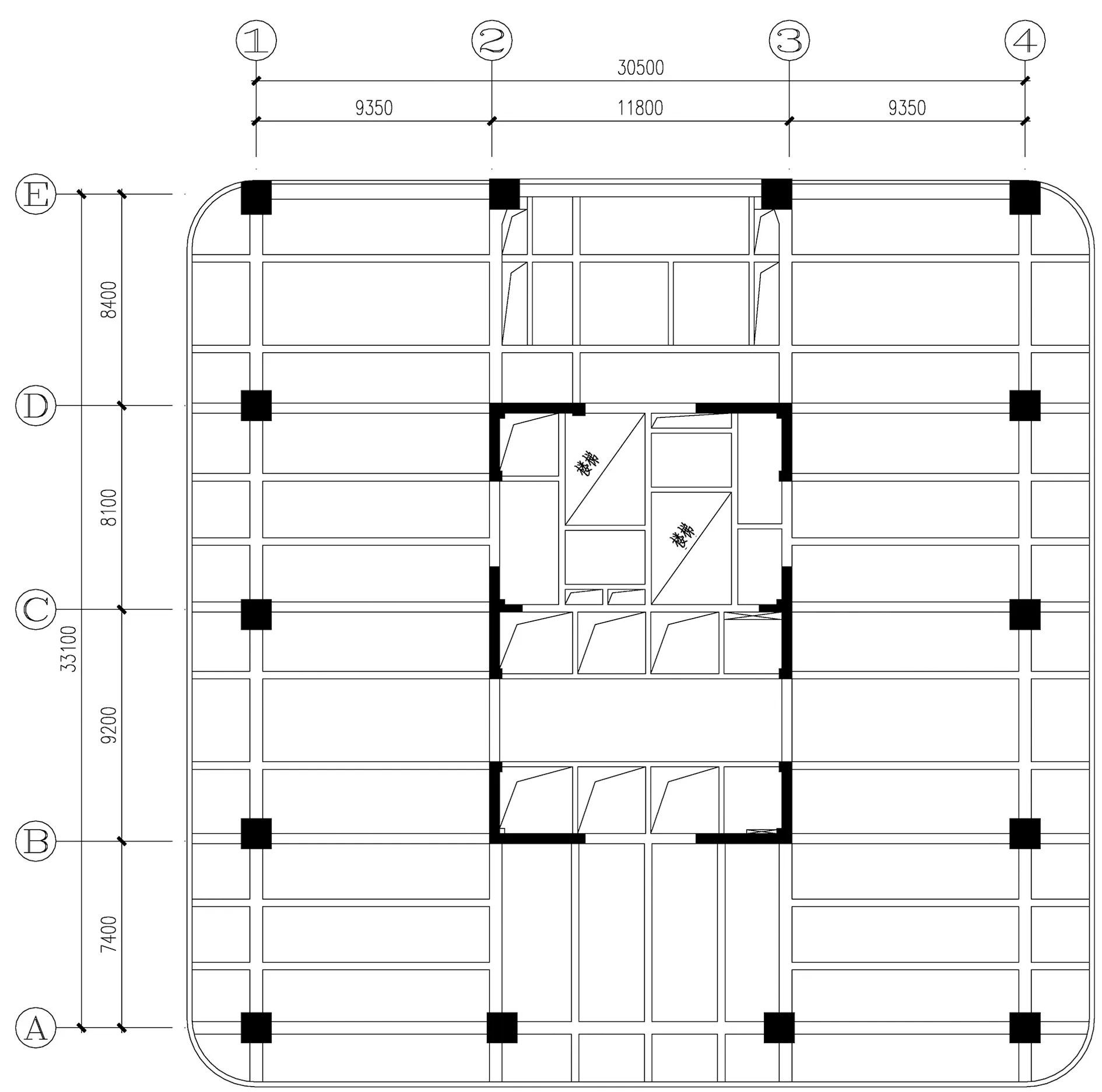
图3 标准层结构平面

该项目现已经建成并投入使用，现场实景立面图如图4所示。

图4 外立面建成实景图

3 结构稳定性分析

根据电算结果，该工程结构刚重比指标如表1所示。

表1 结构刚重比指标

从表1可以看出，结构在X向地震工况下，该结构刚重比EJd/GH2小于2.7，未满足《高规》5.4.1要求，需要考虑重力二阶效应。

实际工程中往往不是这样的，尤其高层办公楼(比如框架-核心筒结构)，往往因为中间设备层、挑空、开大洞或立面收进等等因素，无法满足规范上述的稳定公式推导前提条件。因此，结构等效侧向刚度无法直接采用规范条文说明给出的刚度，计算公式如下：

进行计算，应该采用悬臂梁上的水平集中力的顶点侧向变形公式[3]。由于结构模型将风荷载和地震作用都等效为作用于各层板面标高的集中力，因此，等效侧向刚度公式改写为如式(10)：

(10)

式中：Pi——作用于第i楼层水平荷载;hi——第i楼层层高;H——结构总高度;βi——Hi/H。

基于风荷载作用和地震作用并结合式(10)，该工程等效侧向刚度计算结果如表2所示。

表2 风和地震作用下结构等效侧向刚度

结合式(9)相应结构刚重比计算结果如表3所示。

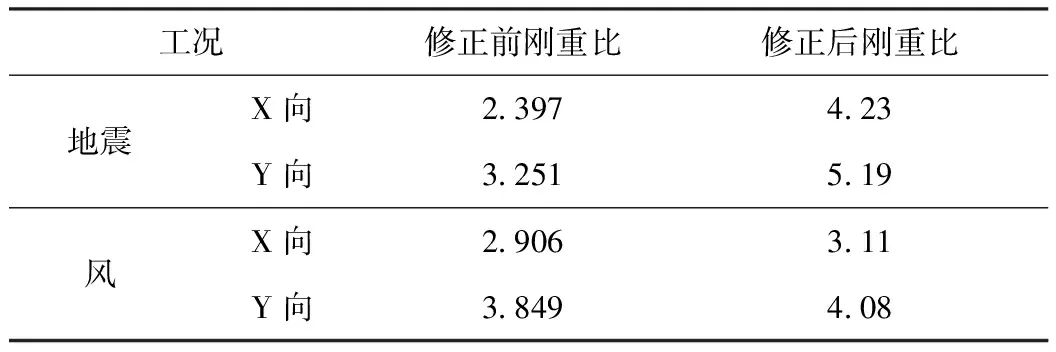
表3 结构刚重比修正前后对比

通过表3可以看出，考虑了结构各层层高及质量不均匀前提下刚重比修正后，结构刚重比均较规范结构有所提高，验算后满足规范对二阶效应的限值要求，结构可以不考虑二阶效应。

4 结构整体稳定屈曲模态分析

《高规》提出，高层结构的重力二阶效应可采用有限元方法进行计算，对整体结构进行整体线性屈曲稳定分析。分析加载工况一般取为全楼的重力荷载代表值。计算公式[6-7]如下：

([K]+λ[KG]{U}=λ{P}

(11)

式中[P]为荷载向量矩阵，λ为荷载系数，[KG]为结构几何刚度矩阵，[U]为结构位移向量；可以理解为屈曲模态,结构上每一点所在的位置连起来的样子；求解(11)式特征方程，特征值行列式值为零，从而求解结构屈曲荷载(即λ[P])和屈曲模态(即[U])。根据上面方程可求解出若干屈曲模态(通解)，也即许多平衡状态。此后，再从较多结构屈曲模态中，甄别分析结构整体最不利对应的屈曲模态。

因此，根据上述(5)(6)式推导可得出：

(12)

式(11)可描述为结构的临界荷载与结构重量的比值若大于11，与《高规》5.4.1-1式概念是等效的，是可以保证结构稳定安全的。同理，根据前面式(5)和△*/△≤1.05条件可推导出：

(13)

即结构在满足式(13)条件下，可不考虑二阶效应。

根据上述式(12)和式(13)，对本工程进行整体稳定线性屈曲分析，结果如图5～图7所示。

图5 第1模态(λcr=20.88)

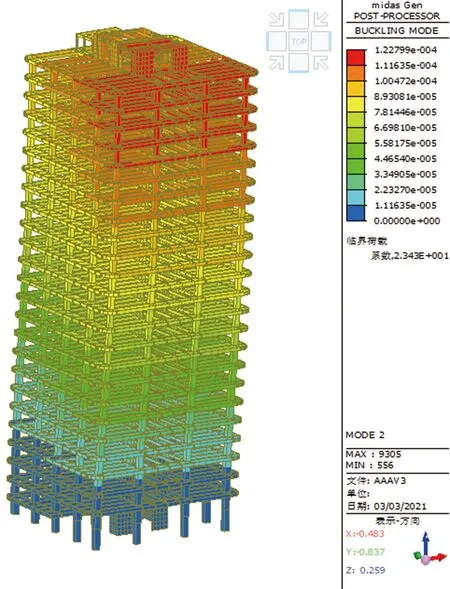
图6 第2模态(λcr=23.43)

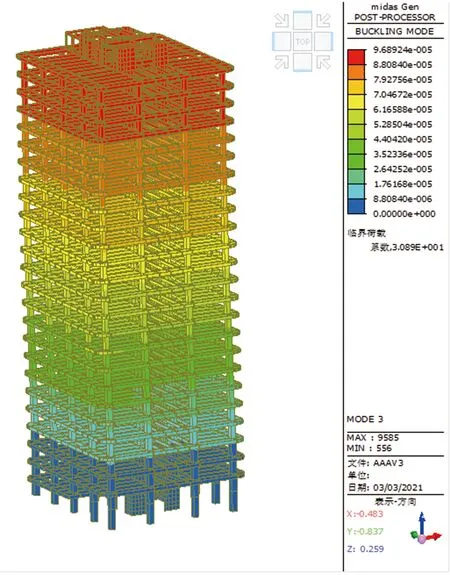
图7 第3模态(λcr=30.89)

上述计算结果表明，整体屈曲各个模态中，对应屈曲因子最小值λcr=20.88也均大于20，满足上述式(13)的要求，结构计算分析可以不考虑二阶效应。

5 结语

从刚重比控制稳定性的理论出发：

(1)对于实际工程结构还可根各层实际层高、质量分布进行理论计算，对规范刚重比进行修正后，复核是否满足结构整体稳定，或是否考虑二阶效应。

(2)规范结构整体稳定计算方法，一般适用于刚度和质量分布沿竖向均匀的结构。对于刚度和质量分布沿竖向不均匀的结构，也可采用有限元分析方法。