考虑时变间隙的并联指向机构非线性模态分析

孙 静 韩雪艳 魏元浩 陈 爽 李仕华

1.燕山大学机械工程学院，秦皇岛，0660042.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，066004

0 引言

并联指向机构作为一种工作性能要求很高的精密设备，必须具有高精度、高可靠性和长使用寿命等特征。机构的支承或构件在生产加工和装配中产生的微小误差以及在各种复杂环境中长期使用后产生的磨损都可能导致机构运动副出现间隙，这些运动副间隙相比结构本身的尺寸可能很小，但是在间隙内产生的零部件接触-分离的碰撞现象会导致刚度的突变，降低机构的运动精度，使其运动轨迹出现非线性波动，令机构出现明显的振动现象[1]，同时也会对机构的模态特性产生影响。固有频率的变化可能会导致不可预测的共振发生，从而大大降低设备的工作精度和使用寿命。然而实际中往往无法直接使用设备样机进行含间隙机构非线性模态实验，因此有必要寻找有效的方法建立含间隙并联指向机构振动模型以对其非线性模态特性进行分析。

模态和间隙振动特性研究是进行含间隙机构动力学优化、寿命预测和故障诊断的基础，国内外学者已经开展了许多相关研究。李艳清等[2]利用加权平均方法对含间隙两自由度弹簧-质量分段振动系统的非线性模态进行了研究。张艳龙等[3]将Dankowicz动摩擦模型引进力学系统中，结合数值仿真方法研究了非光滑因素间隙及摩擦作用下强非线性系统动力学行为。李新泉等[4]建立了一类两自由度含间隙碰撞振动系统动力学模型，并构建了Poincaré映射方程，采用数值计算方法探究了系统的混沌振动特性。唐俊杰等[5]考虑受力变化频繁的关节处运动副间隙，利用有限元软件和静力学计算分析了运动副间隙对机构模态振动特性的影响。尹凤伟等[6]基于一类带有间隙-弹性约束的两自由度受迫振动系统，通过多目标和多参数协同仿真分析，研究了非光滑振动系统的周期性冲击振动特征。ZHAO等[7]研究了一种基于改进变分模式分解的分解技术以自适应提取一系列频域特征，并有效地检测气门机构间隙异常故障。王强等[8]基于模态综合法，结合有限元分析和模态试验对含间隙折叠舵面的非线性动态特性进行了分析。上述文献针对不同特征结构所进行的非线性振动分析多属于仿真以及针对间隙或其他非线性因素的研究，对动态间隙和非线性振动特性之间联系的理论研究并不充分，且研究对象多具有对称特性或为简单机械结构，因此有必要针对考虑运动副间隙的复杂空间并联指向机构模态特性进行深入研究。

本文针对SUN等[9]提出的一种新型3-RRCPR并联指向机构，将数轴法应用到具有复杂空间结构的并联指向机构的振动系统建模中，并验证其可行性；考虑残余刚度，提出含间隙运动副的改进非线性等效刚度系数建立方法，并建立考虑时变间隙的非线性振动模型。

1 含间隙机构振动系统建模

1.1 基于数轴法的机构振动系统建模

图1所示的3-RRCPR六自由度并联指向机构[9]具有3条构造相同的支链，每条支链由固定于基座上的转动驱动副、第1连杆、从动转动副、第2连杆、等效圆柱副和位移驱动副组成，动平台和3条支链的位移驱动电机之间通过转动副连接。机构通过驱动转动副调整姿态，通过微动移动驱动副调整动平台位置。

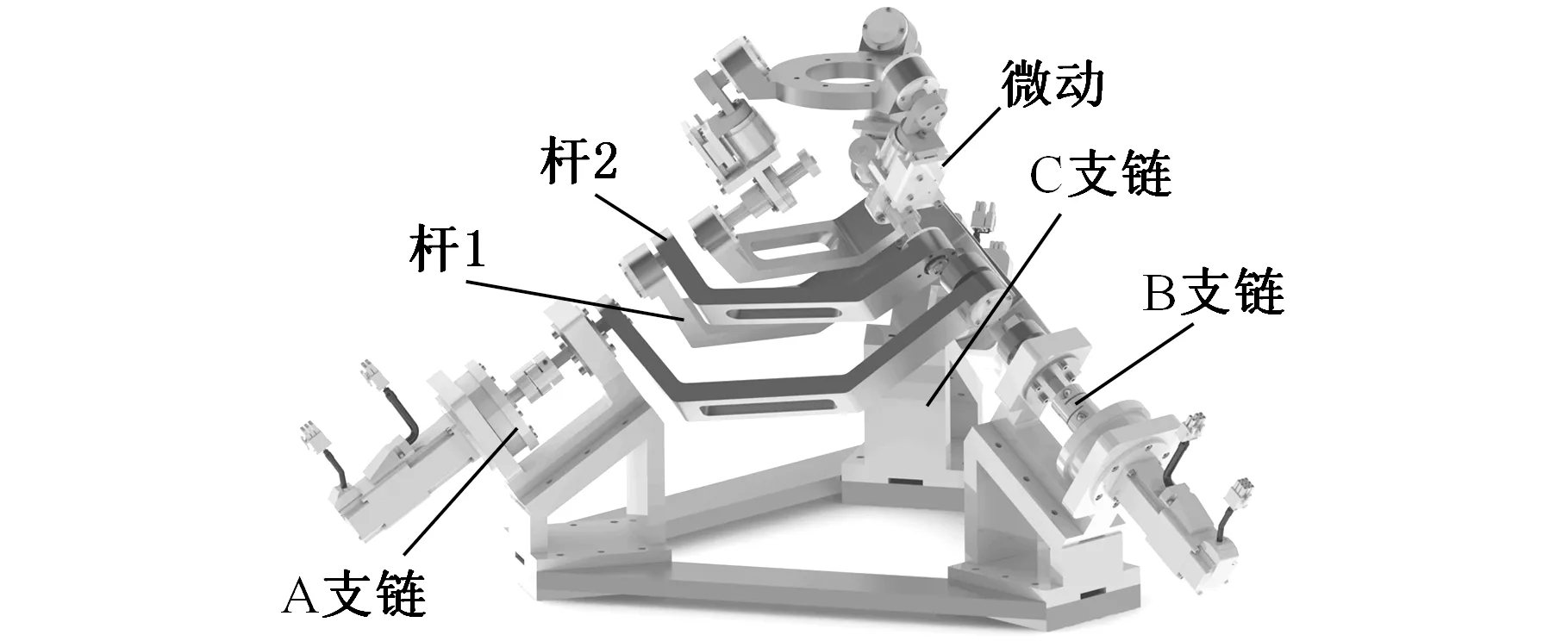
图1 3-RRCPR并联指向机构构型[9]Fig.1 3-RRCPR parallel pointingmechanism configuration[9]

若采用常用的动力学建模方法(如拉格朗日方程等)来对该机构的振动特性进行建模分析，则建模的难度很大，且由于存在大量结构和力传递参数，求解过程也会十分困难，甚至会出现数学模型求解失败的情况,在进行具有针对性的振动模态分析时，若采用此类建模方法，将严重影响分析效率且无法保证能够得到计算结果。

为降低考虑间隙的空间并联指向机构非线性模态建模与求解的难度，本文将数轴建模法[10]应用到图1所示机构的振动模型建模中。由于机构的阻尼和振幅都很小，故将结构中惯性和刚度较大的部件视为质量集中的质点，惯性小且结构刚度较小的部件视为无质量弹簧阻尼系统。机构的基座、驱动转动副和动平台的刚度远大于连杆刚度，振动特性主要受3条支链影响，故在振动建模过程中忽略固定连接处的刚度及上下平台结构刚度，重点考虑连杆特征参数。

考虑到所分析的并联指向机构的运动为低速运动，其工作状态下的自振频率一般较低，且该机构对振动最为敏感的微动结构的垂直方向的振动相比其他方向更为显著，因此本文对所建立的振动系统模型进行了一定程度的简化，选择垂直于动平台的方向为关注的振动方向进行建模。

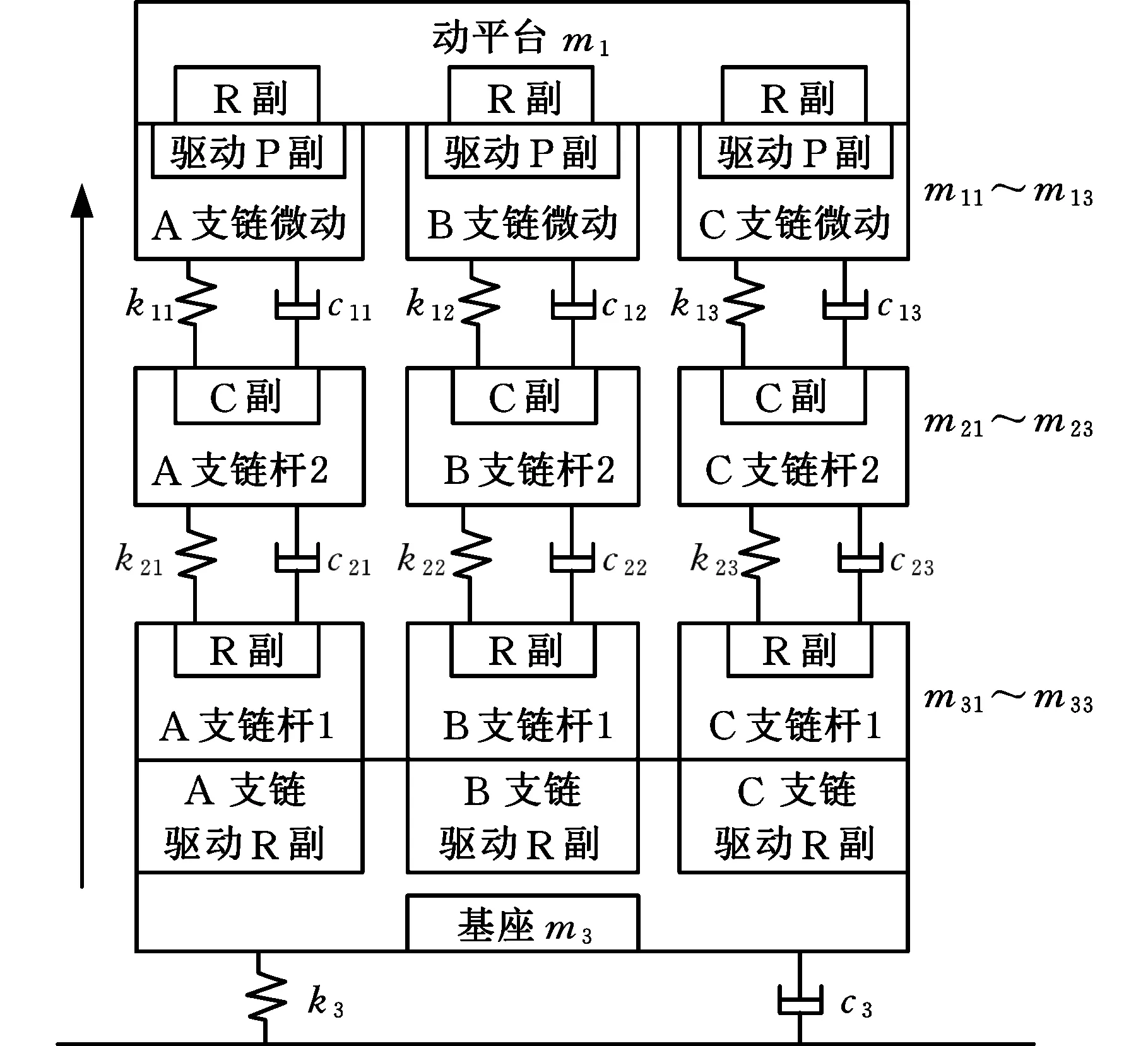
图2 基于数轴法建立的机构振动模型Fig.2 Vibration model based on number axis method

在垂直于动平台的方向上，基于数轴法建立了简化后的3-RRCPR并联指向机构振动模型，如图2所示。图中mi、ki、ci分别为系统的质量、刚度系数和阻尼系数，各个集中质量块所代表的指向机构零部件见图2中标注。R副表示转动驱动副，P副表示移动驱动副。

机构振动系统微分方程为

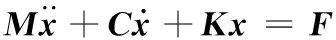
(1)

式中，x为所建立的振动模型中各质量块mi的广义物理坐标的振动位移；M为质量矩阵；K为刚度矩阵；C为阻尼矩阵；F为振动方向上的外力。

利用图2所示的基于数轴法所建立的振动模型，对质量矩阵M、刚度矩阵K和阻尼矩阵C进行构造并将其代入式(1)中，即可较为简便地得到机构的振动模型。

构造的机构质量矩阵M和刚度矩阵K可以表示为

M=diag(m1+m11+m12+m13,m21,
m22,m23,m31+m32+m33+m3)

(2)

(3)

K1=k11+k12+k13K2=k11+k21

K3=k12+k22K4=k13+k23

K5=k21+k22+k23+k3

因为指向机构的阻尼主要是源自材料内的阻力和部件结合面之间的干摩擦[11]，所以选择在机械结构振动分析中广泛应用的瑞利阻尼。阻尼矩阵C可表示为

(4)

c11=α(m1+m11+m12+m13)+β(k11+k12+k13)
c12=-βk11c13=-βk12c14=-βk13
c22=αm21+β(k11+k21)c25=-βk21
c33=αm22+β(k12+k22)c35=-βk22
c44=αm23+β(k13+k23)c45=-βk23
c55=α(m3+m31+m32+m33)+
β(k3+k21+k22+k23)

其中，α、β分别为质量阻尼系数和刚度阻尼系数，可以根据某两阶固有频率确定：

(5)

(6)

式中，ωi、ωj为某两阶固有频率；ξi、ξj为与之对应的两阶模态振型阻尼比。

1.2 振动模型的正确性验证

为验证由式(1)～式(4)所构造的机构数轴法振动模型的正确性，需要利用此模型计算得到的固有频率结果同有限元分析结果进行对比。根据指向机构各部位使用的材料，得到振动模型质量参数数值，如表1所示。

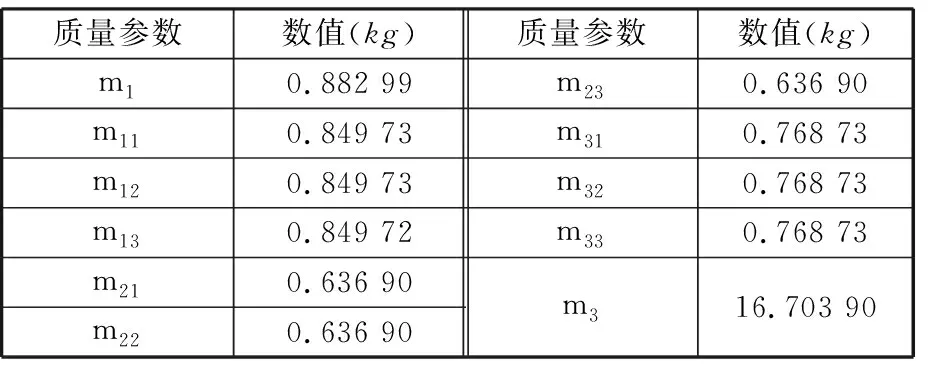
表1 振动模型质量参数

利用静应力分析结合曲线拟合可得到振动模型刚度参数数值，如表2所示。

表2 振动模型刚度参数数值

令并联指向机构振动系统在零初始条件下的初始速度和位移为零，则复平面上的振动响应方程为

(s2M+sC+K)X(s)=0

(7)

式中,s为振动方程经拉氏变换后的复变量；X(s)为广义坐标的振动幅值和方向。

考虑到并联机构的实际阻尼很小，对机构的模态特性影响也有限，本文针对无阻尼非线性振动系统进行分析。忽略式(7)中阻尼参数，并将表1、表2中数值代入式(2)所示质量矩阵和式(3)所示刚度矩阵中，可得无阻尼振动系统的特征方程：

|s2M+K|=0

(8)

进一步可得广义特征方程：

KU=-s2MU

(9)

将矩阵M进行Cholesky分解，即

M=LLT

(10)

由于M为正定对角矩阵，可知L=LT。令A=L-1K，B=LT，可将求解式(8)的问题转化为广义特征值的求解问题：

L-1KU=-s2LTU

(11)

AU=s2BU

(12)

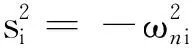
表3 理论模型模态参数计算精度

表3结果显示，理论建模计算结果最大误差不超过5%，符合工程精度要求，证明了该建模方法的可行性。

1.3 考虑残余刚度的改进非线性等效刚度系数

若要将上文所建立的基于数轴法的理想机构振动模型拓展至考虑间隙的机构振动模型中，需要对含间隙运动副内的刚度系数进行定义。

目前研究含间隙运动副的相关文献所使用的间隙接触模型多为图3所示的转动副间隙模型，主要针对轴和轴套之间存在间隙ebj时的非线性刚度kn及法向接触力FN进行研究，含间隙非线性刚度系数在轴与轴套之间发生接触、分离及相互嵌入时，会呈现出多段函数的特征[12]，且以是否分离为边界决定刚度系数是否为零，分离时轴与轴套互不接触。

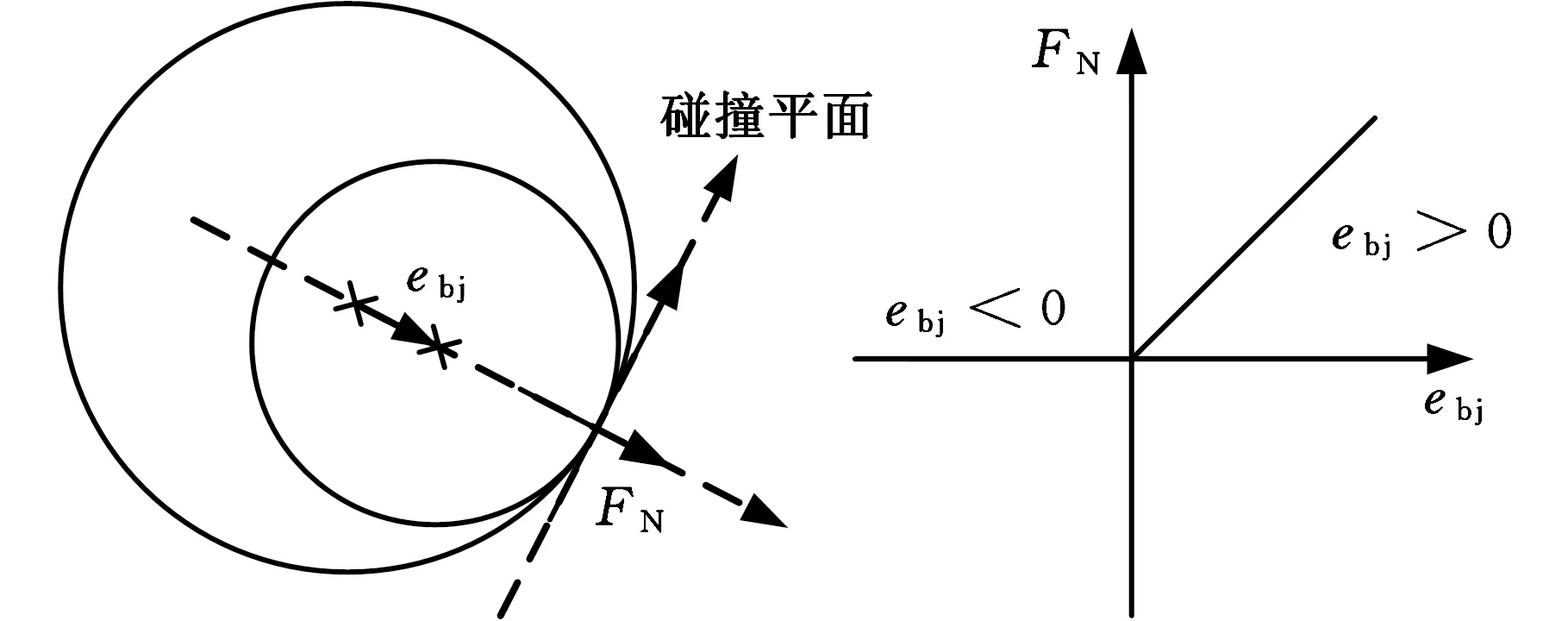
图3 间隙副轴与轴套的接触模型Fig.3 Contact and collision model of clearancecountershaft and bushing

对于并联指向机构的振动模态特性分析，需考虑系统整体的刚度特性。振动模型中的刚度参数不仅需要考虑运动副内的接触支撑刚度，还需要考虑该部位装配特征对局部刚度产生的影响，如阶梯轴支撑面、联轴器的连接等，这些特征可能对间隙内零部件的相对运动产生一定程度的抑制，因此在运动副接触部位由于间隙发生分离时，该处刚度并不会像传统模型中定义的一样为零，而是会出现一定程度的削弱，将此时的刚度定义为残余刚度。因此上述间隙接触等效模型需要进行改进，改进模型中轴套和轴的半径差(即初始间隙)设为ΔR，随机构运动时动态变化的轴套和轴的中心距离(即间隙值)设为δ。

由文献[13]可知含间隙运动副内非线性接触刚度系数

(13)

(14)

式中，l为两间隙接触面的长度；n为力指数；e为两接触面在接触时的变形量，随时间变化；E*为两接触面材料的等效弹性模量；ν1、ν2分别为两接触面材料的泊松比；E1、E2分别为两接触面材料的弹性模量。

令刚度系数ks为运动副接触部位由于间隙发生分离时的残余刚度，kε为间隙处两接触面之间发生接触碰撞时的非线性接触刚度系数，结合以上两参数的多段函数作为改进后的非零含间隙非线性等效刚度系数ke：

(15)

1.4 考虑时变运动副间隙的机构振动系统建模

为了将运动副的间隙特征嵌入由式(1)～式(4)所构造的机构理想振动模型中，将含间隙运动副在图2所示模型中的对应位置上添加间隙ΔR，并用式(15)所建立的考虑残余刚度的非线性等效刚度系数ke代替原始常值刚度系数kr，例如若A支链连杆1、连杆2之间的从动转动副含有间隙，则所构造的含间隙振动模型如图4所示。

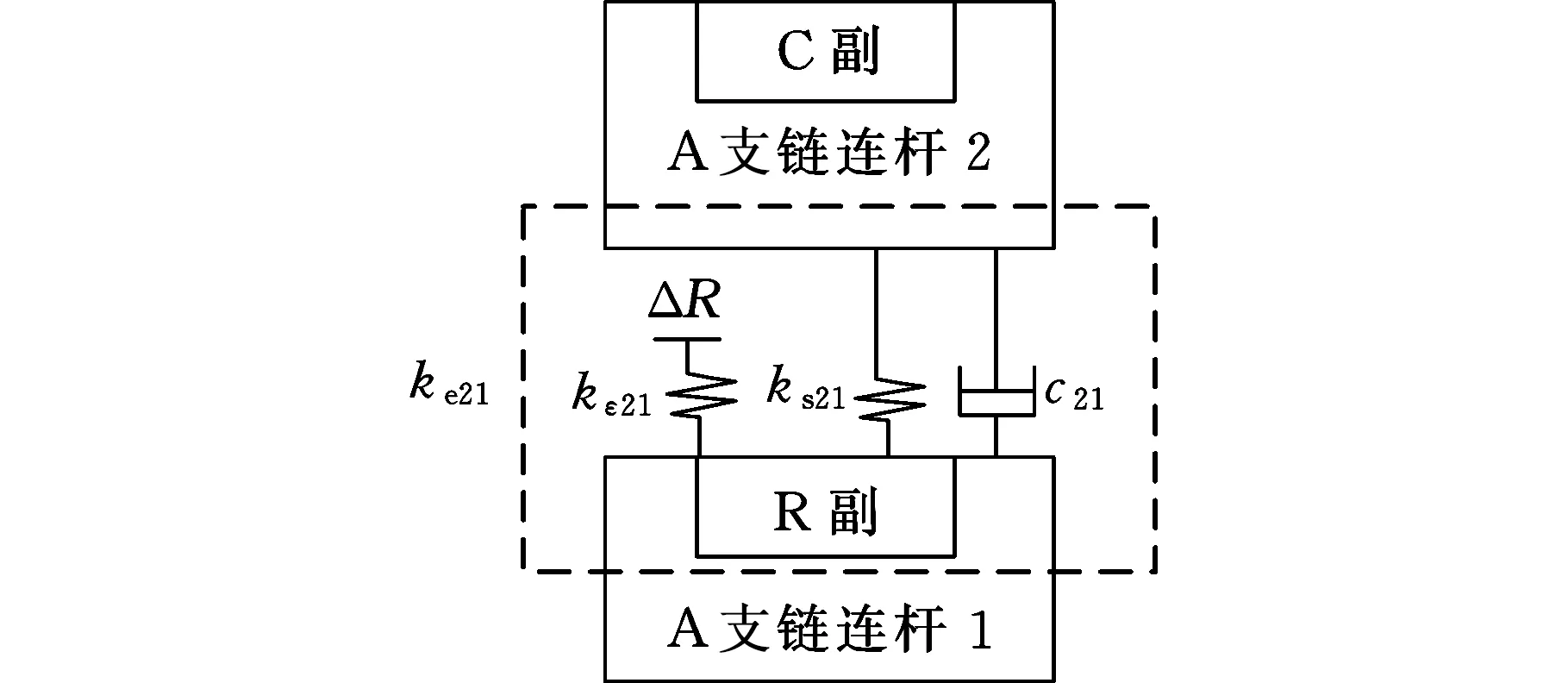
图4 考虑运动副间隙的振动模型Fig.4 Vibration model considering the clearance ofthe kinematic pair

考虑运动副间隙的机构振动系统微分方程为

(16)

式中，Ks为含间隙振动系统的包含残余刚度系数的总体刚度矩阵；FG为振动系统中由于间隙的存在而额外产生的内力[14]。

随着振动系统中含间隙运动副内的间隙值δ的变化，非线性等效刚度系数ke也随之变化，该系数中已包含了含间隙运动副的接触特征，能表征接触部位的任何时刻的刚度特性。将式(16)中的系统内力FG等效为εx，ε作为该振动系统中某些运动副存在间隙时整个振动系统刚度特征的表征符号，本文将其构造为如下形式的含间隙刚度矩阵Ke来对刚度特征进行描述(此处矩阵Ke与图4模型相对应):

(17)

由式(16)和式(17)，考虑运动副间隙机构的振动系统微分方程可以表示为

(18)

并联指向机构中含间隙运动副的类型及数量不同，式(18)所示的间隙刚度矩阵的参数构造也会有所不同，但构造原理和过程是相同的。

已知含间隙振动系统方程的特征多项式为

|s2M+Ke(e)|=0

(19)

综上可建立考虑时变间隙的机构无阻尼非线性振动模型：

(20)

残余刚度ks与原始刚度、间隙特征均有一定联系，本文简化为缩减一定比例的残余刚度ks。

若考虑运动副间隙对阻尼的影响，与建立的改进非线性等效刚度系数类似，可以建立非线性等效阻尼系数 。残余阻尼系数cs与间隙副内接触面发生碰撞摩擦时的非线性阻尼系数cε[15]共同构成含间隙机构振动模型的非线性等效阻尼系数ce。振动系统中各项的阻尼系数cs及cε分别构成阻尼矩阵Cs及Cε，由Cs及Cε即可构造出非线性等效阻尼矩阵Ce。

Cs(cs)=αM+βKe(e)

(21)

(22)

(23)

式中，g为恢复系数，与材料本身的性质有关；v0为接触碰撞前的速度。

进而可以建立考虑时变间隙的有阻尼机构振动模型：

(24)

2 考虑时变间隙的机构非线性模态分析

2.1 并联指向机构间隙动力学仿真

若要分析考虑时变间隙的3-RRCPR并联指向机构非线性模态特性，需要得到机构含间隙运动副内的间隙数据δ，这里通过ADAMS中建立的含间隙动力学模型并进行仿真分析来实现数据的获取。

考虑到所分析机构的结构和负载特征，对存在间隙时的机构支链上连杆1和连杆2之间的从动转动副以及基座上驱动转动副进行动力学仿真分析，利用反馈控制力矩方式在间隙动力学仿真中模拟电机驱动；根据运动副的装配特征设置仿真模型的间隙运动副连接；调整间隙运动副的接触碰撞参数以尽可能减少接触碰撞的失真；在最容易发生振动的滚珠花键处参考日本THK公司LF系列滚珠花键的参数设置摩擦参数。这些设置使仿真模型尽可能符合工程实际。由于现阶段对复杂并联指向机构进行含间隙动力学实验时在成本和实现难度等方面还存在较大问题，尤其是变化的间隙特征难以在实验中进行实时测量，因此通过理论模型结合间隙动力学中已有大量应用的ADAMS仿真工具对机构非线性模态进行研究，可以为这类问题的研究提供一定理论依据。间隙动力学仿真模型如图5所示。

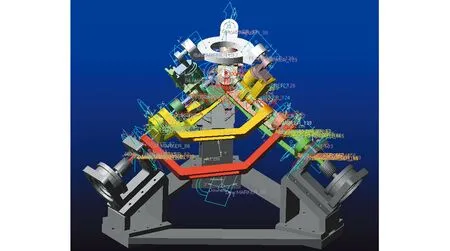
(a)并联指向机构仿真模型

仿真条件设置如下：A支链驱动转动副转速10°/s，驱动时间5 s，即驱动转角0°～50°，设置驱动转动副间隙为0～0.5 mm，第1、第2连杆之间的从动转动副间隙为0～5mm，分别对存在不同间隙特征的机构进行间隙动力学仿真。

由于本文分析所得到的机构含间隙动力学仿真间隙数据图较多，故仅以机构A支链的驱动转动副出现0.1 mm间隙且驱动转速为10°/s时情况为例进行展示，并联指向机构的含间隙运动副内位移如图6所示。

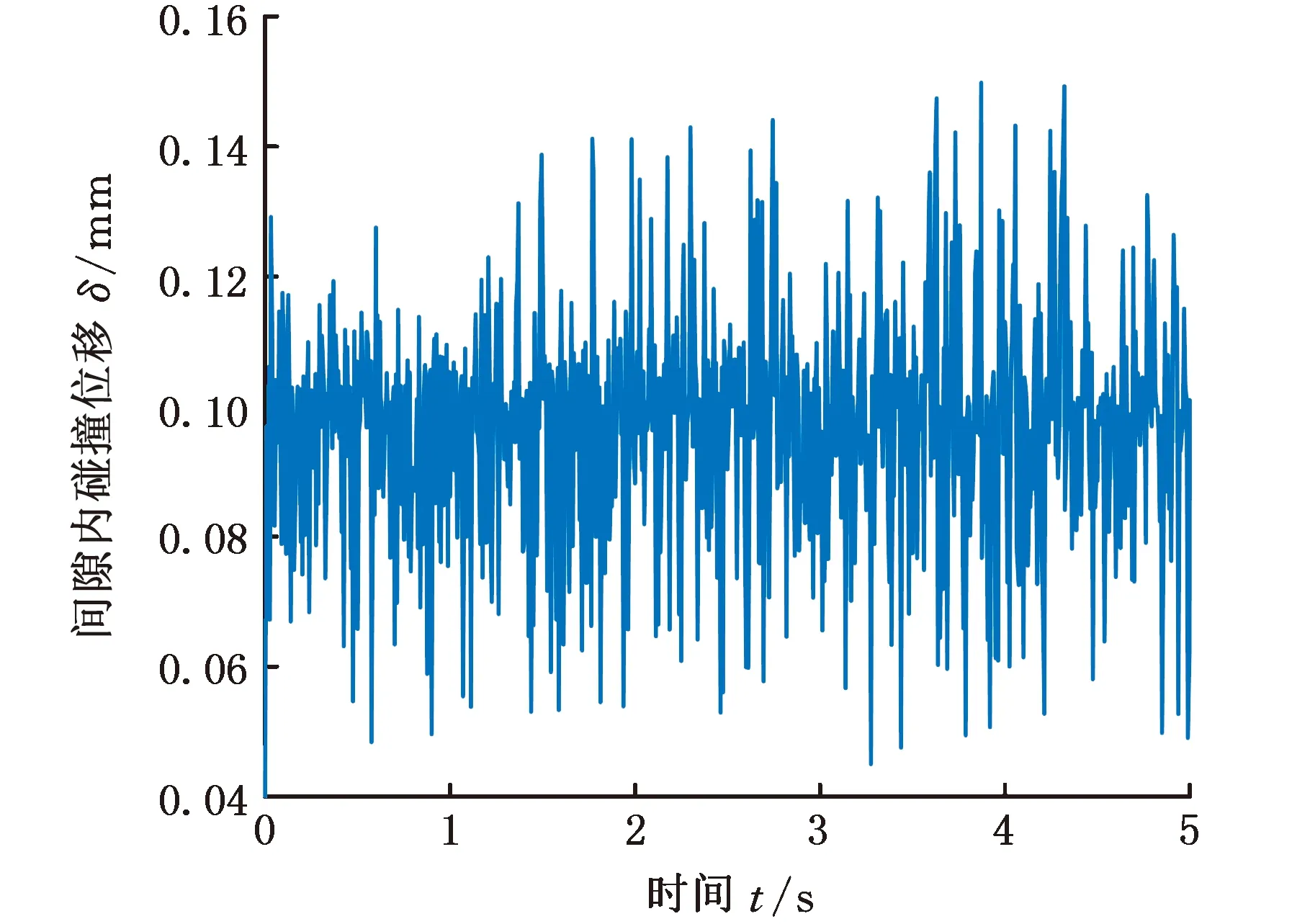
图6 指向机构含间隙驱动转动副内位移Fig.6 Pointing mechanism with clearance drive andinternal collision displacement of rotating pair

2.2 改进的非线性等效刚度系数ke求解

通过ADAMS仿真可以得到式(15)中的非线性等效刚度系数ke中的间隙位移参数δ，其他参数如表4所示。

表4 非线性接触刚度系数kε的已知参数

由表4中的参数结合式(14)可求得接触面材料的等效弹性模量E*为113.5 GPa。根据式(15)，在MATLAB中建立对应的数学模型，并将机构中含间隙运动副的对应刚度系数设置为变量，然后将ADAMS仿真得到的间隙数据作为数值矩阵导入该数学模型中，结合式(13)、式(14)求得非线性等效刚度系数ke。图7、图8所示为当A支链驱动转动副和从动转动副分别出现0.1 mm、0.2 mm和0.3 mm的间隙时，间隙副内非线性等效刚度系数的变化情况。

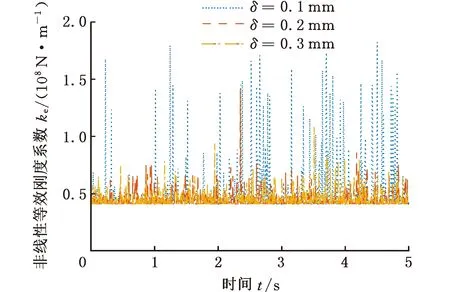
图7 含间隙驱动副非线性等效刚度系数变化Fig.7 Nonlinear equivalent stiffness coefficient changeof driving pair with gap

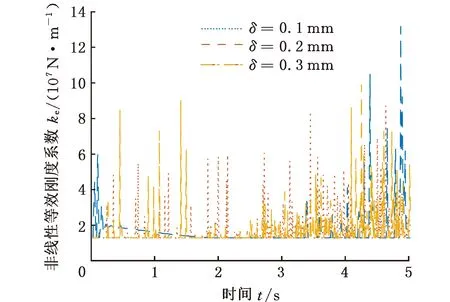
图8 含间隙从动副非线性等效刚度系数变化Fig.8 Variation of nonlinear equivalent stiffnesscoefficient of driven pair with gap

并联指向机构的驱动转动副固定于基座上，空间位置不随机构运动变化，故间隙副内碰撞运动主要受重力、间隙值和转速因素的影响。由图7、图8可知，当转速为10°/s时，随着驱动转动副间隙值的增大，含间隙非线性等效刚度瞬时突变峰值有所衰减；从动转动副由于位于连杆连接处，空间位置会随连杆运动发生变化，此时相比于转动副间隙值的大小，重力和连杆空间交错位置会对间隙副内碰撞运动产生更为显著的影响，在一定转速下连杆转角处于0°～10°和30°～50°时非线性等效刚度突变峰值较大，明显出现相较于10°～30°区域更激烈的接触碰撞。

2.3 含间隙并联指向机构模态特性分析

将上文求解得到的非线性等效刚度系数代入形如式(17)的含间隙刚度矩阵中，有

Ke(e)=K(ks,kε(e))

(25)

而在q个时刻内，随着间隙变化的时变非线性等效刚度系数可构成数组{ke}q，将其代入含间隙刚度矩阵式(17)中，则可得三维含间隙刚度矩阵：

(26)

将此矩阵代入式(20)所示的考虑时变间隙的无阻尼非线性振动模型中，即可求解时变模态固有频率。将运动副出现不同间隙值时指向机构的时变模态固有频率进行整合，即可得到机构的模态固有频率分布域。

本文针对在A支链驱动转动副0°～50°转动范围内，驱动转动副以及第1连杆、第2连杆之间的从动转动副分别出现0～0.5 mm的间隙，以及支链上的驱动转动副和从动转动副同时出现0～0.5 mm的间隙时，机构的非线性模态固有频率分布域进行了分析，其结果见图9～图11。

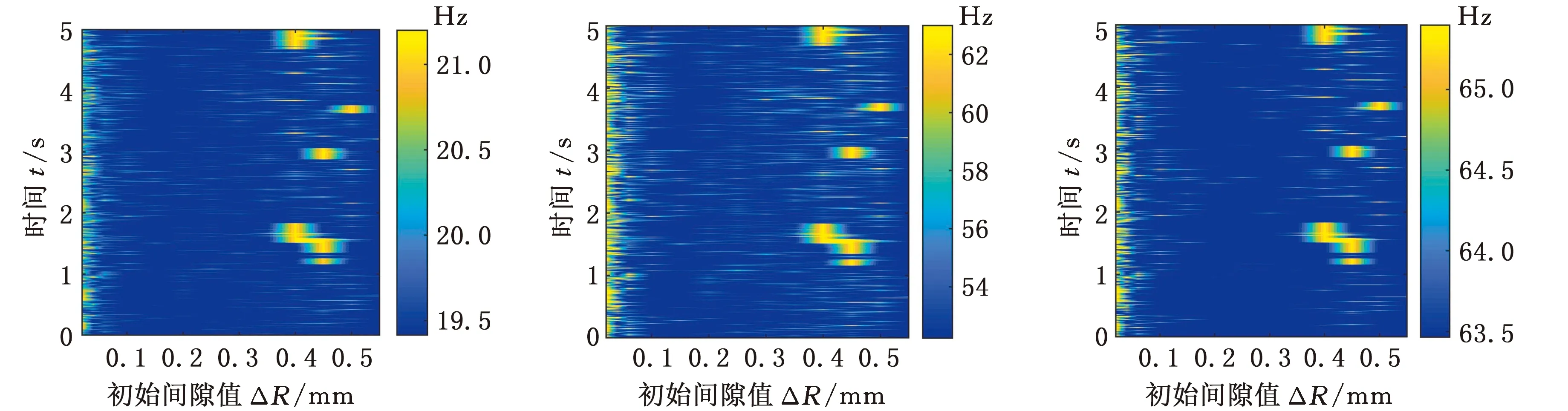
(a)1阶固有频率 (b)2阶固有频率 (c)3阶固有频率

(a)1阶固有频率 (b)2阶固有频率 (c)3阶固有频率

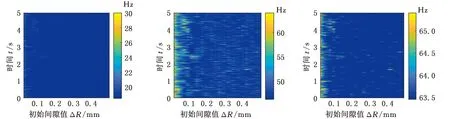
(a)1阶固有频率 (b)2阶固有频率 (c)3阶固有频率

由图9～图11可知，驱动转动副和从动转动副的不同间隙值对并联指向机构非线性模态产生的影响有明显不同。驱动转动副间隙的存在会使固有频率出现短时间内的剧烈突变，这种现象在间隙值为0.4～0.5 mm时尤为明显；从动转动副间隙则会使固有频率出现较为均匀的波动，且在机构转角较大时更加明显；当两种间隙同时存在时，产生的耦合效应又会使频率分布域呈现不同的特点，可以较为直观地看出除了第2阶固有频率之外的几阶波动都明显减弱。

为了更为直观地了解含间隙运动副对指向机构模态固有频率的影响，依据图9～图11整理了如图12和表5所示的并联指向机构模态固有频率波动范围图。

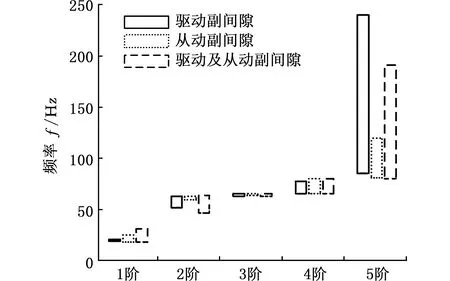
图12 不同间隙特征影响下模态固有频率波动Fig.12 The modal natural frequency fluctuation underthe influence of different gap characteristics

表5 模态固有频率波动上下限

分析图9～图12和表5可知，并联指向机构运动副存在0～0.5 mm间隙时，含间隙运动副的非线性等效刚度的瞬时变化会使机构模态固有频率发生波动。驱动副间隙影响下模态分布域波动较为均匀，大范围波动集中在间隙0～0.1 mm和0.4～0.5 mm处；从动副间隙影响下模态分布域波动主要集中在机构初始位置和第1连杆30°～50°转动范围内；机构的驱动转动副和从动转动副同时出现间隙时，机构的第1和第3～第5阶模态固有频率的分布域波动会大大减弱，几乎只存在于间隙值0～0.1 mm范围内，只有第2阶模态固有频率分布域仍然存在明显的均匀波动，且对第1、2阶模态频率的波动上下限影响也明显增大，波动上限增加了5～6 Hz，而对5阶模态频率的上下限影响与单驱动副间隙时相比有所降低，分析后判断是由于多个间隙的耦合使得支链的柔度有所增加，机构的高频振动得到一定抑制，低频高振幅的振动影响更加显著，这会使得机构各阶固有频率分布域尤其是第1阶的波动次数明显降低，但第1、2阶波动的幅度会有所提高。

理论模型计算的5阶模态中，第5阶模态对运动副间隙较为敏感，在发生接触时，频率波动可达40～150 Hz，且驱动副间隙对模态固有频率的影响与从动副相比更为显著；第1～第4阶模态在不同运动副间隙特征的影响下波动范围较小，整体不高于15 Hz。这说明机构在低阶工作频率下具有较好的稳定性。

3 结论

(1)3-RRCPR并联指向机构单个支链的驱动转动副在0°～50°转角范围内，驱动转动副出现间隙时，机构的非线性模态固有频率会出现较为均匀的时变波动，且在间隙值为0～0.1 mm、0.4～0.5 mm时波动较为明显；从动转动副出现间隙时，会使机构固有频率在初始位置和连杆30°～50°转动范围内出现较为频繁的波动；驱动副和从动转动副同时出现间隙时，机构第2阶之外的模态固有频率波动频繁程度会明显降低，但是第1、第2阶的波动上下限会出现5～15 Hz的变化；机构的第5阶模态固有频率对运动副间隙的敏感度远大于第1～第4阶，其波动值至多是第1～第4阶模态的数10倍，这说明在并联指向机构某一从动副、驱动副或两者同时出现间隙时，机构的1～4阶固有频率数值不会发生过大的突变，也说明了在低频域下运转时该机构具有较好的稳定性。

(2)本文的研究内容可以为所分析的3-RRCPR机构的动态性能优化、结构共振域分析、故障预测等供理论分析依据，也可以为其他复杂机构的振动模态建模分析提供一种可行的研究方法和思路。