管道攀爬机器人非接触变磁隙式永磁吸附机构的设计与吸附性能优化

2021-08-02郭登辉

中国机械工程 2021年14期

郭登辉陈原

山东大学机电与信息工程学院，威海，264209

0 引言

长期的海水锈蚀以及大量海洋生物附着和侵蚀将降低石油管道的承载能力，严重影响管道的使用寿命，所以对管道的清理已成为保证管道使用寿命和安全生产的重要方法。机器人清理技术以其高效的作业效率、较强的适应能力和安全的生产模式使机器人清理技术具有广泛的应用前景。

管外攀爬机器人是水下作业的载体。铁质管道管外攀爬机器人主要是永磁吸附式攀爬机器人，按吸附方式可分为接触式和非接触式。目前，国内外学者对永磁吸附攀爬机器人的研究已经有了一定的成果[1-11]。接触式磁吸附管外攀爬机器人虽然结构简单且能够提供稳定的磁吸附力，但无法克服永磁吸附机器人的运动灵活性与吸附力之间的矛盾。非接触式变磁吸附攀爬机器人虽然可以通过调节磁隙的方法克服运动灵活性与吸附力之间的矛盾，但是对于复杂的曲面，由于磁铁的固定形状会造成磁吸附力的剧烈变化，导致磁能利用率降低和负载能力受到限制，无法满足不同直径和重载下的作业要求。

磁吸附单元的优化设计方法有对比分析法和一阶优化方法[12-15]。对比分析法可以通过单一变量寻找磁吸附单元的最优尺寸和排布方式，但由于磁铁宽度的变化会对单位体积的磁吸附力的极值和波动幅度等多个参数有影响，所以通过控制变量进行对比分析的方法不能得到最佳磁铁宽度；而利用ANSYS提供的一阶优化方法是对连续函数的一阶偏导数进行优化，不适合对离散数据进行优化设计。

本文设计了一种非接触变磁隙式管道攀爬机器人，能够通过磁吸附机构自动适应不同曲率的管道变化，并通过优化算法得到磁吸附单元的最优磁铁宽度。

1 非接触变磁吸附式管道攀爬机器人的创新设计

海底管道攀爬机器人必须具备可靠的吸附能力、平稳运动能力以及灵敏的壁面适应能力。本文设计的非接触变磁吸附式管道攀爬机器人应能在直径1～2 m的管道表面稳定爬行，且具有最大20 kg的负载能力。相对于电磁吸附，永磁吸附方式无需提供电源设备和无需担心中途断电的危险，而且工作时间长，磁吸附力大，所以本文采用永磁吸附方式。

引入3个参数来描述机器人磁能利用效率和稳定性:

λ=F/V
η=Fmin/Fmax
v=(Fmin-Fmax)/d

其中，λ为单位体积的磁吸附力，代表机器人磁能利用效率；η为同一宽度、不同直径下磁吸附力的最小值Fmin与最大值Fmax之比,η值越大其稳定性越好；v为单位宽度的磁铁磁吸附力的最大变化幅度，用来衡量磁吸附力的波动幅度，v值越小其稳定性越好；F为磁吸附力；V为永磁体体积；d为方形磁铁的宽度。为了最大限度地提高负载能力和稳定性，λ应在满足η与v的前提下取最大值。

本文设计了图1所示的非接触变磁吸附式管道攀爬机器人。机器人由直径检测机构、吸附机构和移动机构组成，能够实现直径的实时监测、磁吸附力自动调节、轴向移动和周向转动等功能。直径检测机构能够自动检测管道的直径变化，并可控制吸附机构自动调整磁隙和磁吸附单元的结构来自适应不同曲率的工作表面。如图2所示，直径检测机构由固定板和移动件组成。当与工作表面接触时，移动件会相对于固定板产生移动，通

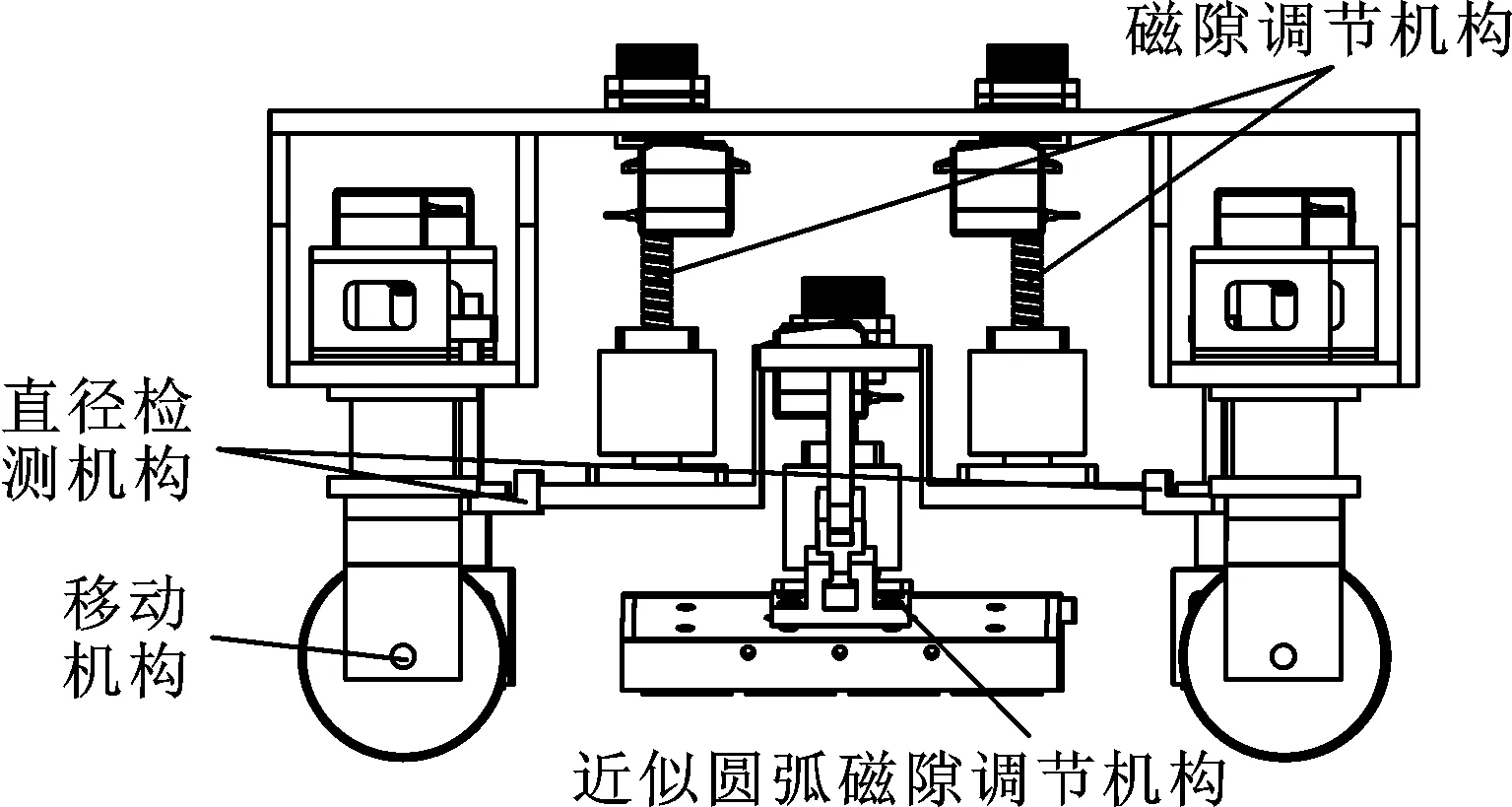
(a) 非接触变磁隙式攀爬机器人机构的组成

图2 直径检测机构Fig.2 Diameter detection mechanism

过位移传感器得到移动件的位移量δ。由于两个固定件之间的距离s固定，位移量δ和半径r是一一对应的，所以半径的大小可以通过下式获得：

吸附单元位于爬壁机器人的中心位置，如图1d所示。吸附机构由近似圆弧磁隙调节机构和磁隙调节机构两部分组成。磁隙调节机构由两个丝杠机构组成，用来控制整个近似圆弧磁隙调节机构的磁隙大小。近似圆弧磁隙调节机构由磁铁板组成，为了减少电机的个数和节约空间，采用3块磁铁板组成近似圆弧机构，且每个磁铁板镶嵌若干完全相同的方形磁铁。当直径检测机构检测到直径变化时，由丝杠机构调节中间移动磁铁来使3块磁铁板构成近似圆弧；接下来，由磁隙调节机构调节整个近似圆弧磁隙调节机构的磁隙变化；移动机构如图1c所示，由驱动电机和旋转舵机驱动4个轮子做轴向移动和周向转动。当爬壁机器人由轴向移动变为周向转动或由周向转动变为轴向移动时，可通过旋转舵机改变轮子的移动方向来控制爬壁机器人的运动模式。

2 非接触变磁吸附机构建模

2.1 运动学建模

为了使吸附机构能够自适应不同直径的管道变化，本文设计了图2所示的直径检测机构和图3所示的近似圆弧磁隙调节机构，用来调节磁隙的变化。近似圆弧是指由转动副连接的所有磁铁板在执行机构的作用下自适应形成与管道表面切线平行的多边形曲面。直径检测机构由固定件和移动件组成，它能够检测管道的直径，并使移动件做出相应的位移变化，然后将变化的直径信号传递给控制单元来调节近似圆弧磁隙调节机构的运动。如图2所示，移动件的位移可以表示为

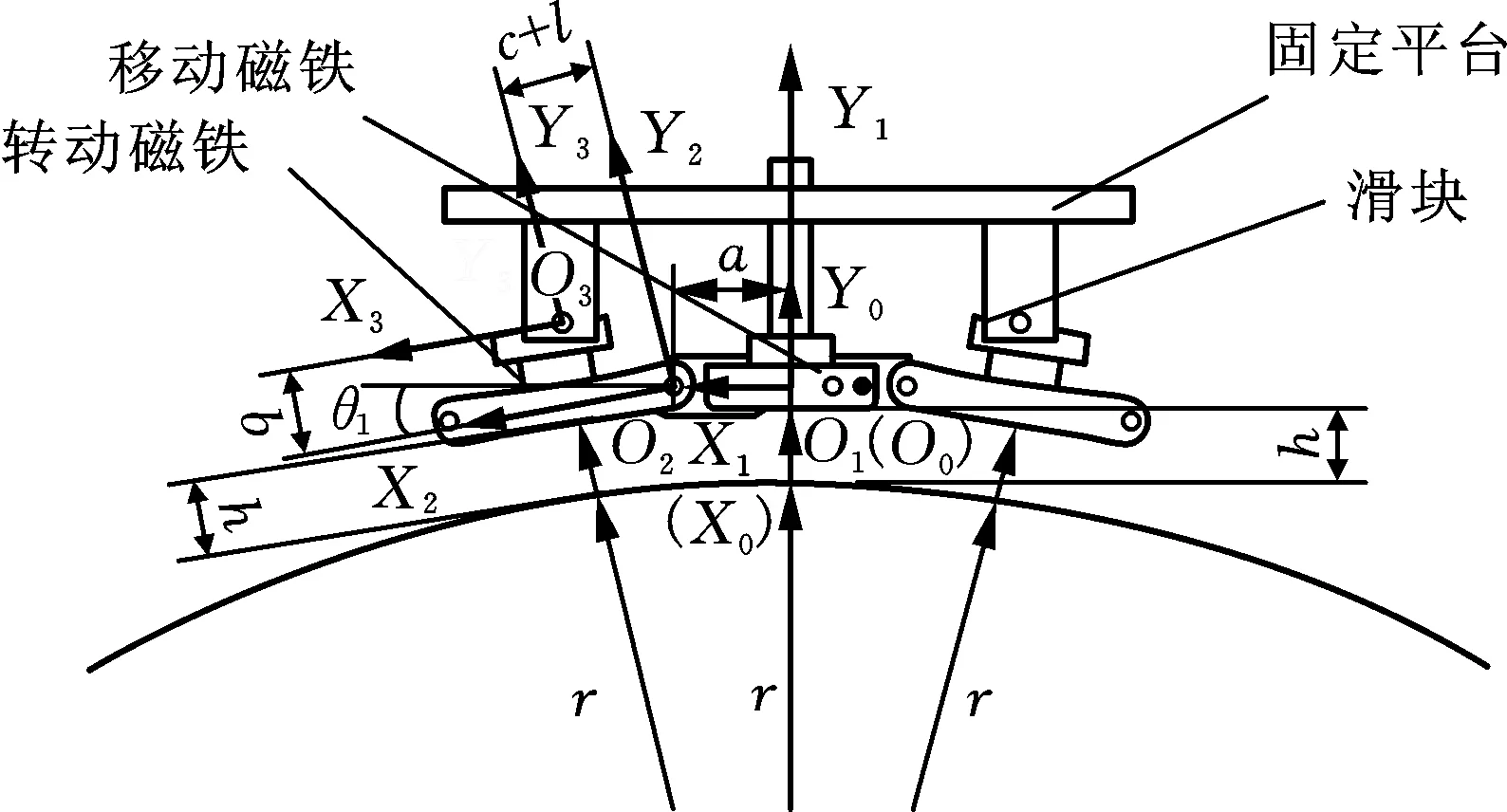
图3 近似圆弧磁隙调节机构Fig.3 Approximate circular arc magnetic gap adjustment mechanism

如图3所示，通过D-H参数法分别在移动磁铁、旋转磁铁和滑块上建立O1X1Y1,O2X2Y2,O3X3Y3坐标系统。初始状态下静坐标系O0X0Y0与动坐标系O1X1Y1完全重合，O1X1Y1沿O0X0Y0的Y0轴移动，位移δ与直径检测机构中移动件的位移相同。O2X2Y2相对于O1X1Y1的转动角度为θ1，O3X3Y3相对于O2X2Y2的相对移动量为l。O3X3Y3相对于O0X0Y0的转换矩阵可以表达为

其中，Trans(Y0,δ)表示O1X1Y1沿Y0轴移动位移量δ；Rot(Z2,θ1)表示O3X3Y3绕Z2轴转动θ1；l为O3X3Y3相对于O2X2Y2的相对移动量。通过坐标变换可得

(1)

式中，c为O3在坐标系O2X2Y2中的初始横坐标；b为O3在坐标系O2X2Y2中的纵坐标。

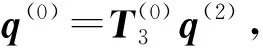
(2)

利用式(2)通过MATLAB仿真可以得到图4所示的旋转磁铁相对位移量l和转动角度θ1随活动磁铁位移的变化曲线。由图2可知，移动磁铁位移δ随着管道半径r的减小而增大。从图4中可以看出，当移动磁铁位移δ逐渐增大(即管道半径r逐渐变小)时，其旋转磁铁的相对位移量l和转动角度θ1逐渐增大。当移动磁铁运动时，如图2所示，旋转磁铁通过转动副绕轴心O3转动θ1，使旋转磁铁与工作表面的切线平行。3块与工作曲面切线平行的磁铁板形成与工作曲面相似的圆弧形态，如图1d所示。这种均与工作曲面切线平行的近似圆弧形态能够改变整体磁铁吸附单元与工作表面磁隙的分布，从而提高磁吸附力和磁能利用效率。

图4 旋转磁铁角度、位移-移动磁铁位移曲线Fig.4 Rotating magnet angle, displacement-moving magnet displacement curve

2.2 磁场理论模型

标量磁位法和矢量磁位法是计算永磁体外部空间磁场的基本方法[16]。标量磁位法通过等效磁荷模型进行求解且等效磁荷模型仅具有一个自由度；而矢量磁位法通过等效电流模型进行求解，具有3个自由度。根据本机构的对称分布特点，只需求得一个方向的矢量磁位即可，所以选用矢量磁位法对永磁体对应的磁感应强度进行求解。

根据麦克斯韦方程组，静态磁场基本方程为

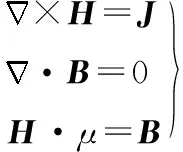
(3)

式中，H为磁场强度；B为磁感应强度；J为电流密度；μ为相对磁导率。

由磁通连续性，矢量磁位A与磁感应强度B之间的关系可以表达为

(4)

式中,AX、AY和AZ分别为X、Y和Z方向的矢量磁位。

通过式(3)、式(4)可得矢量磁位的泊松方程:

(5)

由磁通连续性定理和安培环路定理可知磁铁表面和其他不同介质交界面处的磁场强度满足下式：

(6)

式中,S表示除了永磁体表面的不同介质交界面；S′表示永磁体表面；n表示S和S′的法线方向；S+、S-分别表示进、出磁铁表面。

通过等效电流模型与毕奥-萨伐尔定理可得距离为h处的平面磁感应强度：

(7)

式中,BZ为求解点处Z方向的磁感应强度；R为永磁体内源点到外部磁场求解点的矢径。

本文所采用的磁铁为铷铁硼N35，方形永磁铁长×宽×高为(2w)×(2w)×h0。在其下表面中心处建立空间直角坐标系，X、Y方向分别为方形磁铁的长和宽方向，Z方向为磁铁高度方向。对式(7)进行体积分，可求解出距离方形磁铁上表面Z处的磁感应强度BZ为

(8)

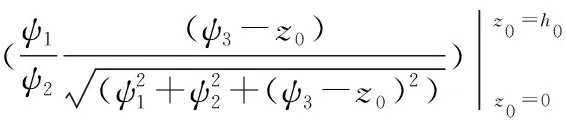
式中，z0为磁铁内部到磁铁吸附表面的垂直距离；h0为磁铁的总厚度。

当距离磁铁上表面h处为平面(图5a)时，其法向吸附力设为F1，磁感应强度设为

BZ1=BZ(x,y,z)

(9)

当距离磁铁上表面h处的平面变为半径为r的曲面(图5b)时，A1位置处的法向吸附力设为FZ1,磁感应强度为

(10)

当磁铁到Z轴距离为x1时，A0位置处的Z方向吸附力设为FZ2,磁感应强度为

(11)

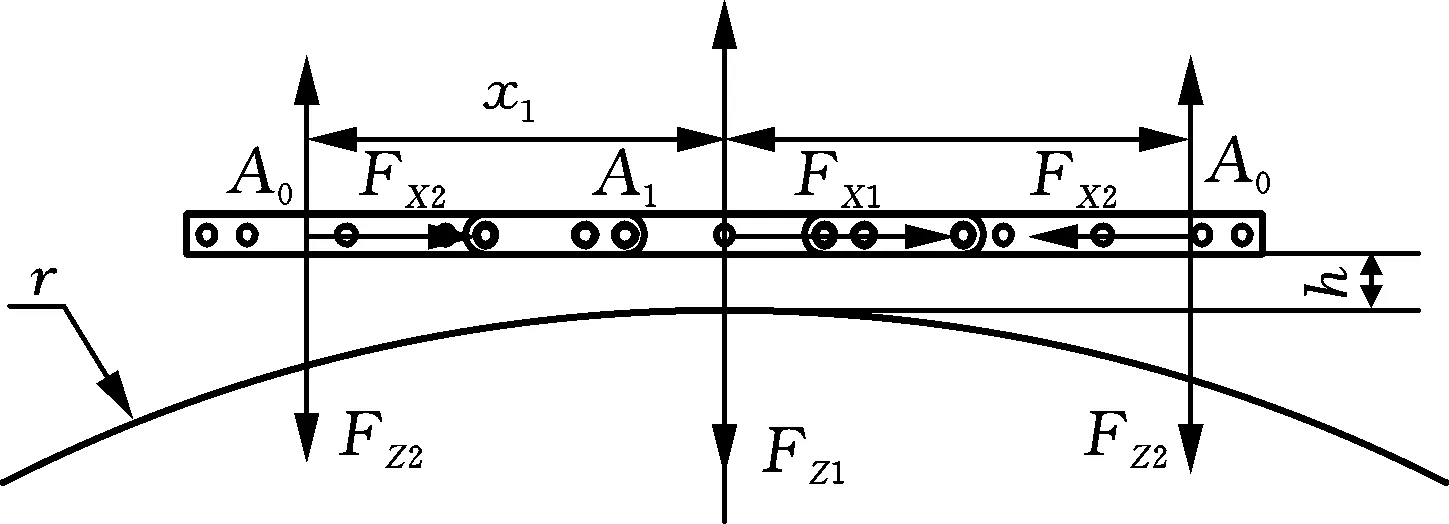
(a)平面矩形磁铁

2.3 磁吸附力理论建模

计算磁吸附力的方法有中心磁感应强度法[17-18]和有限元模拟法[19-20]。本文计算的曲面磁感应强度分布复杂，所以采用有限元模拟法来计算磁吸附力，磁吸附力可以表达为

式中，μ0为空气磁导率；N为对磁铁拆分的单元数量；i为第i等分磁铁单元；Bi为每一等分的磁感应强度；Si为每一等分气隙的有效受力面积。

图5所示为3块方形磁铁组成的平面磁铁和近似圆弧型磁铁在直径为1 m的管道所形成的磁吸附力分布图，由图5b可知，近似圆弧磁隙调节机构的3块磁铁均在A1位置，所以Z方向的吸附力

F2=FZ1+2cosθ1FZ

(12)

式中，FZ1、FZ均为磁铁在A1位置产生的法向磁吸附力。

平面磁铁的分布如图5a所示，两侧磁铁在A0位置，中间磁铁在A1位置，所以Z方向的吸附力

F3=FZ1+2FZ2

(13)

3 非接触变磁吸附式攀爬机器人的磁吸附力计算和优化

3.1 力学建模

建立图6所示的爬壁机器人静力学模型。保证爬壁机器人能够稳定运行的条件是：机器人能够沿壁面稳定行走而不滑移、不倾覆。基于以上条件建立爬壁机器人的力学模型：

(14)

式中，Ff1、Ff2、Ff3、Ff4分别为4个轮子的静摩擦力；FN为吸附机构提供的磁吸附力；F1、F2、F3、F4为壁面对轮子的支持力；G为爬壁机器人的重力；L为前后轮中心之间的距离；b1为重心O到后轮之间的距离；h1为重心O到壁面之间的距离；β为作业壁面的倾角。

图6 攀爬机器人静力学分析Fig.6 Static analysis of climbing robot

由于爬壁机器人的各个机构均呈对称分布，所以壁面对轮子的支持力F1与F2、F3与F4分别相等，摩擦力Ff1与Ff2、Ff3与Ff4分别相等。为保证机器人能够稳定在壁面运行，壁面对各轮子的支持力应大于0，爬壁机器人轮子所承受的静摩擦力应小于最大静摩擦力。所以可得下式：

(15)

式中，μ1为轮子与壁面之间的静摩擦因数。

利用式(14)和式(15)，通过MATLAB建模得出图7所示的爬壁机器人稳定作业时所需要的磁吸附力和角度β之间的关系。当磁吸附力小于零时，表明此时不需要磁吸附力作用便可保持爬壁机器人不下滑，保持爬壁机器人不下滑所需要的最大磁吸附力FN=2100 N。在倾覆状态下，保持机器人稳定的最大磁吸附力FN=600 N。所以，机器人能够保持稳定运行所需要的最小磁吸附力FN=2100 N。

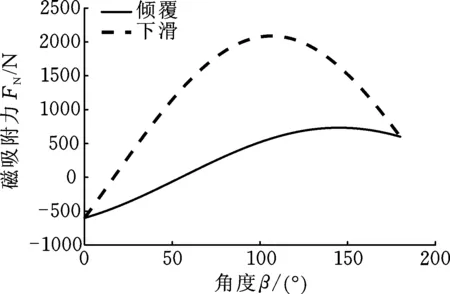
图7 磁吸附力变化曲线Fig.7 Magnetic adsorption force changing curves

3.2 磁场优化

磁吸附机构优化的目的是在满足负载能力的条件下最大限度地提高磁能利用效率和为曲面作业环境提供稳定的磁吸附力。由式(7)可以看出，磁吸附力的大小与磁铁厚度和单块磁铁板上整体磁铁的宽度有关，除此之外轭铁厚度对合理设计磁路和提高磁吸附力也有一定的影响。当最小磁隙为5 mm时，单块磁铁在最小圆柱半径处的最大磁隙不得超过10 mm，所以单块磁铁板上整体磁铁的宽度应小于140 mm。负载和结构要求使得宽度应大于40 mm。

基于控制变量法和Maxwell仿真分析，得到图8所示的磁吸附力随着磁铁厚度和轭铁厚度的变化曲线，其中磁铁均为边长为40 mm的方形磁铁。从图8中可以看出，磁铁厚度对磁吸附力的影响较大，磁吸附力会随着磁铁厚度的增大而迅速增大，当磁铁厚度大于15 mm时，磁吸附力逐渐趋于稳定。轭铁对磁吸附力的影响相对较小，当轭铁厚度增加到17 mm时，其磁吸附力逐渐稳定，并达到饱和状态。所以规定磁吸附单元磁铁厚度为15 mm和轭铁厚度为17 mm。

图8 磁吸附力随磁铁厚度和轭铁厚度变化曲线Fig.8 Curve of magnetic attraction with magnet thickness and yoke thickness

磁铁宽度不仅影响到单位体积磁铁的磁吸附力λ的大小，而且与磁吸附力的最大值与最小值之比η和变化幅度v也紧密相关。单块磁铁板的总体磁铁宽度过大会降低磁能利用效率，且增加磁吸附力的波动幅度，总体磁铁宽度过小又会降低机器人的负载能力。所以，通过控制变量的方法寻找能够同时具有最大磁吸附力和最佳稳定性的最优磁铁宽度是不可行的。

通过Maxwell仿真分析得到了磁隙为5 mm时不同磁铁宽度d=[dj]在不同管道直径时的最大磁吸附力Fmax=[Fmaxj]与最小磁吸附力Fmin=[Fminj]。其中[dj]为不同的磁铁宽度组成的矩阵；[Fmaxj]和[Fminj]为对应的不同dj对应的最大磁吸附力和最小磁吸附力矩阵。由分析可知，单位体积磁铁的磁吸附力λ随着磁铁宽度的增大呈先增大后减小的趋势。根据λ的变化趋势，求解最优磁铁宽度可以通过离散变量的组合型法。目标函数和约束方程为

minf(x)=-(Fmax+Fmin)/(2d2)
s.t.Fmin-ηFmax≥0
Fmax-Fmin-vd≤0
40 mm≤d≤140 mm
Fmaxn1≤Fmax≤Fmaxn2
Fminn1≤Fmin≤Fminn2
η=Fminj/Fmaxj
v=(Fminj-Fmaxj)/dj

式中,Fmaxn1、Fminn1分别为磁铁宽度d=40 mm的最大磁吸附力和最小磁吸附力；Fmaxn2、Fminn2分别为d=140 mm的最大磁吸附力和最小磁吸附力;j表示第j块磁铁。

令η和v的初始值设定为0.8和2 N/mm，其值会随着重复使用离散复合型法次数的增加而逐渐增大。在满足初始约束条件的前提下，利用离散复合型法的多次迭代和提高约束条件中的η和v，可以逐渐缩小约束空间直到寻找到最优解。当首次运用离散复合法得到最优解时，得到满足约束条件的3个自变量的离散区间，宽度区间dj1≤d≤dj2，最大磁吸附力区间Fmaxj1≤Fmax≤Fmaxj2，最小磁吸附力区间Fminj1≤Fmin≤Fminj2，其中下标j1和j2分别代表每次优化后宽度区间与最大最小磁吸附力区间的下界和上界。可以表达为

每个磁铁宽度dj所对应的最大和最小磁吸附力为Fmaxj和Fminj，首次迭代计算得到的最优解所用的参数dj1、Fmaxj2和Fminj2的序号不同，所以求得的最优解并不正确。但是，通过首次迭代计算得到了在约束条件η=0.8和v=2 N/mm下3个自变量组成的离散边界，缩小了求解空间。在此基础上，通过提高约束条件η和v，并通过离散复合型法不断缩小求解空间和提高约束条件，直至序号相同就得到了满足约束条件的最优解。通过离散组合型法得到的最优磁铁宽度对应的参数见表1，目标函数的收敛曲线如图9所示。通过表1可知，单位体积磁铁的磁吸附力λ1=0.0078 N/mm3，那么磁铁板(镶嵌着面积为200 mm×80 mm的磁铁)产生的磁吸附力FZ=1920 N。将FZ代入式(12)可得非接触变磁吸附机构产生的磁吸附力F2=5629 N。这证明了磁吸附机构产生的磁吸附力远大于失稳状态需要的最小磁吸附力。

表1 优化参数

图9 目标函数的收敛曲线Fig.9 Convergence curve of objective function

3.3 磁场与磁吸附力的仿真分析

本文采用边长为100 mm、厚度为15 mm的正方形磁铁，根据式(9)～式(11)，利用MATLAB建模仿真，得出了图10所示3种情况下的磁感应强度分布。从图10a中可以看出，平面磁场的磁感应强度在磁铁中心处出现磁谷，四周有磁峰，磁场分布较为均匀。由图10b可知，当磁铁在A1位置时，磁隙的变化导致磁铁中心处出现磁峰，磁感应强度开始呈现不均匀分布。由图10c可知，当磁铁在A0位置时，由于磁隙的不均匀性增加，导致磁感应强度的分布也不均匀，且磁峰向磁隙较小的方向偏移。通过对比分析可得，磁铁在A1位置产生的磁感应强度比A0位置强，且磁场分布较为均匀。这证明图5b所示的近似圆弧磁隙调节机构能够有效地提高磁感应强度和改善磁场分布。

(a) 平面磁场

利用相同的磁铁，通过Maxwell软件仿真分析得出图11所示3种情况下的磁感应强度矢量分布。由图11可以看出，3种情况下磁感应强度矢量分布和图10所示的磁感应强度分布相同，这证明了磁感应强度矢量理论模型的正确性。为了分析磁感应强度的大小和分布特点，令式(8)y=0，在MATLAB软件中建模仿真可得图12所示3种情况下磁铁中心处的磁感应强度分布曲线。由图12可知，相对于A0处的磁感应强度，磁铁在A1处的磁感应强度更强且分布更为均匀。

(a) 平面磁场

图12 磁铁中心处的磁感应强度Fig.12 Magnetic induction at the center of the magnet

为了对比近似圆弧磁铁和矩形磁铁的效果，通过Maxwell软件仿真分析得出图13a所示磁铁在A0和A1位置磁吸附力随磁隙的变化曲线。由图13a可知，随着磁隙的增大，磁铁在A1位置的磁吸附力远大于A0位置的磁吸附力。将图13a中磁吸附力代入式(12)和式(13)，得到矩形磁铁和近似圆弧磁铁的磁吸附力随磁隙的变化曲线，如图13b所示。当磁隙为5 mm时，近似圆弧磁铁产生的磁吸附力为F2=2251 N，矩形磁铁产生的磁吸附力为F3=1346 N，那么单位体积的近似圆弧磁铁单元产生的磁吸附力λ2=F2/V2=0.0078 N/mm3，大于单位体积的矩形磁铁所产生的磁吸附力λ3=F3/V3=0.0047 N/mm3。与矩形磁铁相比可以得出，近似圆弧磁隙调节机构能够有效提高不同曲率工作表面的磁吸附力和磁能利用效率。

(a) A1和A0位置

4 实验设计与研究

实验样机如图14所示，通过螺栓调整移动磁铁板的位移使3块磁铁板形成与圆柱曲率对应的近似圆弧。在直径1 m的铁制管道上，通过拉力测试装置吊装重物的方法检测磁吸附力的大小。验证实验中，磁隙为5 mm,测量单块磁铁板上不同宽度的方形磁铁产生的磁吸附力大小。在近似圆弧磁隙调节机构与矩形磁铁磁吸附力的对比实验中，通过调节螺栓控制整体磁隙的大小，为了减小实验误差，多次测量磁吸附力，取平均值作为结果。