基于叶尖定时原理的叶尖振幅与叶根动应变关系的试验研究

2021-08-01刘美茹焦江昆郜伟强敖春燕乔百杰

燃气涡轮试验与研究 2021年6期

肖潇，刘美茹，，焦江昆，郜伟强，敖春燕，乔百杰

(1.中国航发四川燃气涡轮研究院，成都 610500；2.西安交通大学机械工程学院，西安 710049)

1 引言

获得叶片动应变分布是进行航空发动机转子叶片设计和高周疲劳寿命预测的前提[1-2]。传统的叶片振动测量是采用接触式方法，通过在叶片上粘贴应变片测量动应变来实现[3]。接触式方法对试验件结构改装较大，高温环境下应变片存活率低，且无法实现叶片服役周期振动的在线监测。

近年来，基于叶尖定时的非接触振动测试系统已广泛应用于压气机、风扇等转子叶片的振动测量。德国MTU公司研究人员基于自主研发的BSSM叶尖定时系统，在压气机试验器上通过安装几支叶尖定时传感器，来获取压气机在颤振工况下的一扭模态振动[4]。美国HOOD 公司已研发出商用的非接触振动测试系统，且已广泛应用于发动机压气机和涡轮转子叶片振动测试[5-6]。天津大学段发阶团队提出了基于叶尖定时信号处理的叶片同步和异步振动分析方法，研制出了基于叶尖定时的非接触振动测试硬件系统[7-10]。北京化工大学王维民将叶尖定时技术应用于涡轮机叶片同步振动参数辨识研究，提出一种只需要少量传感器就可获得较高测量精度的叶片同步振动参数分析方法，并进行了建模仿真和试验验证[11-12]。中国航发四川燃气涡轮研究院将非接触振动测试系统应用于航空发动机整机、核心机以及压气机转子叶片的振动测试，监测转子叶片振动；同时该系统在叶片排故中也取得了较好效果[13-14]。

目前行业内相关研究大多仅涉及到叶片振动频率的辨识，较少涉及叶片动应力重构且不成熟。然而，高精度动应力的获取是叶尖定时能否成功取代应变片测量的关键。本文以某型发动机转子叶片为试验对象，设计了整体叶盘，在模拟转子试验器上，使其在一定的工作转速范围内运行，叶片发生一阶共振现象。同时基于叶尖定时技术和应变片测试方法，采集叶片叶尖振幅和叶根动应变信号，并据此确定叶尖振幅和叶根动应变之间的关系。

2 旋转叶片非接触振动测试原理

2.1 旋转叶片非接触振动测试基本原理

基于叶尖定时的非接触振动测试原理如图1所示。在机匣上安装多支光纤传感器，测量叶片的到达时间。叶片无振动时，各叶片旋转1 周到达传感器的时间相同，只与转子转速和机匣直径有关。叶片振动时，叶片旋转1 周到达传感器的时间会发生变化，与叶片振动幅值和频率有关。由于叶片通过1支传感器只采样记录1次，传感器的采集数据不满足耐奎斯特采样定律，属于欠采样信号，所以不能采用传统的基于傅里叶(FFT)框架的算法分析，但可以通过特定的算法处理得到相应的振动信息[15-16]。

图1 基于叶尖定时的非接触振动测试原理Fig.1 Principle of non-contact vibration measurement based on blade tip timing

2.2 非接触振动测试系统同步振动分析方法

非接触振动测试系统的叶片同步振动分析方法，分为单自由度拟合(SDOF)算法和周向傅里叶拟合(CFF)算法[17]。SDOF 算法的原理是采用单支传感器检测叶片升降速运行的振动，获取叶片不同相位下的共振曲线，包含叶片共振的幅值和共振转速信息。结合叶片坎贝尔图获得激励阶次，可计算振动频率。因此，SDOF 算法适用于转子叶片升降速测试，但对于叶片共振频率和幅值的辨识精度较低。CFF 算法将叶片振动假设为简谐振动，且叶片旋转一圈转速不发生改变；对于每个转速或时间点下，将数据拟合为周向正弦波振动曲线。采用这种方法需要在机匣周向上布置至少3支光纤传感器。CFF算法的优点在于它可以识别叶片耦合振动下的响应，可输出每个转速或时间点下叶片的振动幅值、相位和偏差，与应变片做的阶次跟踪结果非常类似。

2.3 叶尖振幅与叶根动应变的理论关系

根据经典力学分析原理可知，受迫激励下叶片振动响应的动力学方程[18]为：

式中：M 为质量矩阵；C 为阻尼矩阵；K 为刚度矩阵；F 为激振力幅值向量；y为叶片有限元模型的节点位移矢量。

当叶片发生单模态共振时，频域内叶片任意点的位移响应和应变响应分别为：

式中：ω为振动频率，Y(ω)为叶尖位移响应，ε(ω)为叶根动应变，F(ω)=[f1,f2,....,fn]T为叶片激励矢量，Hd(ω)为叶尖位移频响应函数矩阵，Hε(ω)为叶根动应变频响应函数矩阵。

令叶片的自由度为n，将频响应函数写作矩阵形式，则位移、应变响应分别为：

式中：H(ω)中第i行和第j列Hij(ω)元素，指仅在叶片第j点上有简谐激励而相应于第i点的复频响应函数，则第i点对在第j点的简谐力的位移和应变频响应函数分别为：

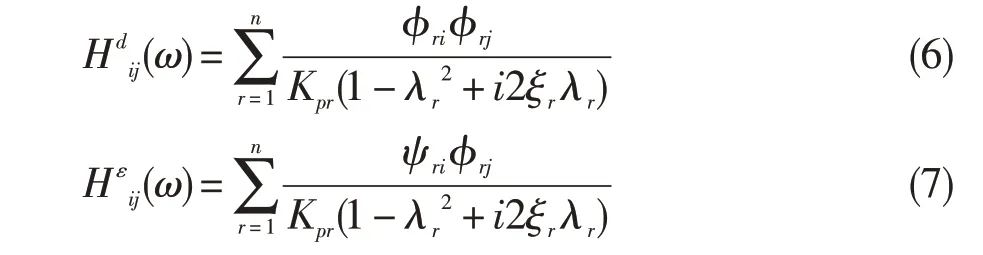
其中：ϕri为响应点i的第r阶模态振型，ϕrj为激励点j的第r阶模态振型，ψri为响应点i的第r阶应变模态振型，Kpr为第r阶的主刚度，λr为激励频率与系统第r阶固有频之比，ξr为系统第r阶阻尼比。

当叶片发生s阶共振，即r=s时，此时激励频率与系统第s阶固有频率接近，即ω=ωs，第s阶主振动起主导作用，其他阶的振动可忽略。则叶片发生s阶单模态共振时，令叶片最大应变为εi s，叶尖位移为yj s，获得最大应变点i的应变响应和叶尖位移点j的位移响应的比值为：

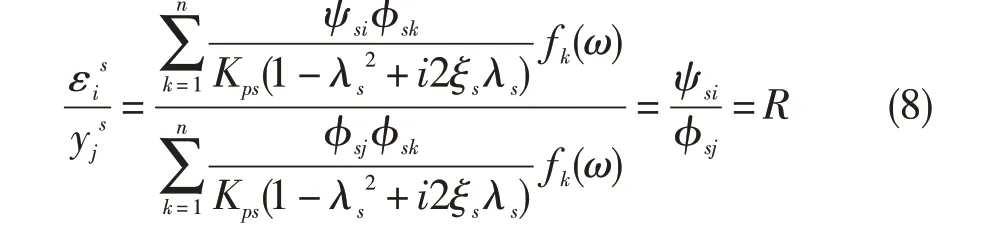
式中：k表示叶片的第k个自由度，ψsi为最大应变点i的第s阶应变振型，ϕsj为叶尖位移点j的第s阶位移振型，ϕsk为第k点的第s阶位移振型，Kps为第s阶的主刚度，λs为激励频率与系统第s阶固有频率之比，ξs为系统第s阶阻尼比。

由公式可知，当叶片发生单模态共振时，叶片最大应变点处应变与叶尖位移振幅有固定的比例关系，且该比值与叶片的模态振型有关，即比值R与叶片的固有属性有关而与外载激励等无关。

3 叶片振动特性有限元分析

图2示出了模拟转子整体叶盘的三维模型。叶盘盘缘直径为68 mm，叶片沿叶高长度为50 mm，叶型为无扭直叶片。采用有限元分析方法对叶片振动特性进行分析。根据叶盘循环对称的结构特点，取1/5的盘和1个完整的叶片作为计算模型。采用ANSYS 软件进行有限元网格划分，划分单元选用SOLID187 带中间节点的四面体单元，最终有限元模型如图2(b)所示。

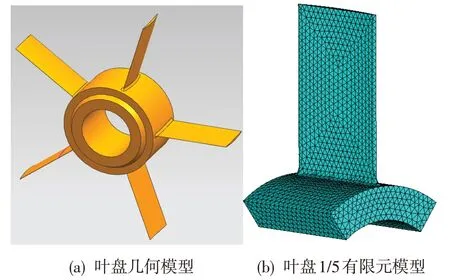
图2 整体叶盘三维模型Fig.2 Three dimensional geometry of simulation blisk

分析坐标系为柱坐标系，坐标原点为积叠轴与发动机轴线的交点。X向为径向，背离发动机轴线为正；Z向为轴向，顺气流方向为正；Y向由右手法则确定，叶背指向叶盆为正。施加的强度计算边界条件和振动计算边界条件为：在循环对称面上施加位移协调一致边界条件，约束盘中心孔位置1 圈节点的轴向和周向自由度。通过ANSYS 模态分析可知模拟转子叶片前6阶静频和对应模态振型，见表1。

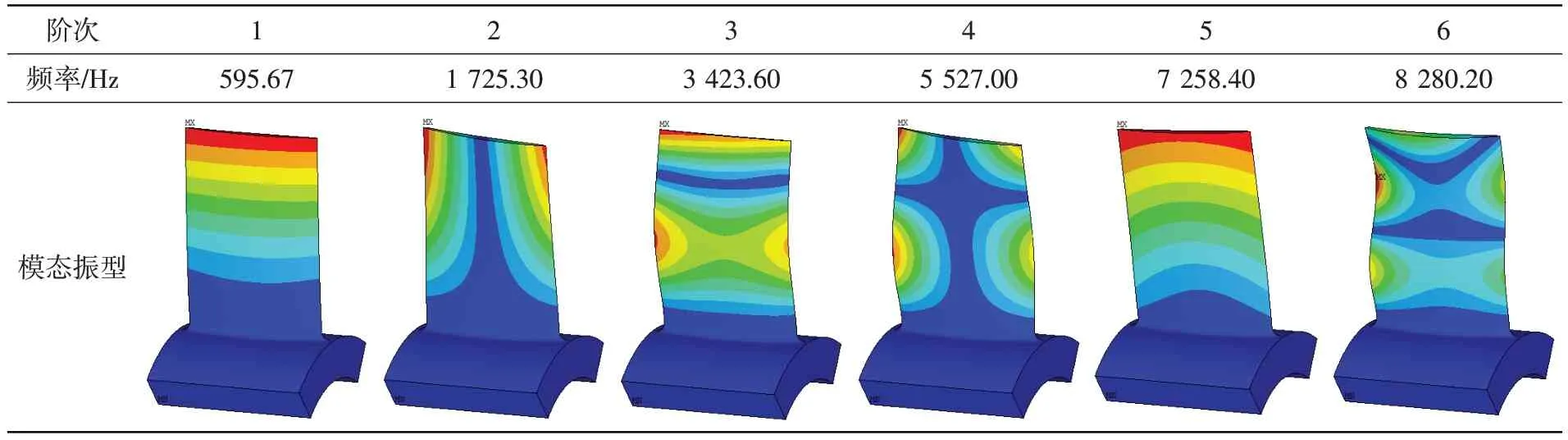
表1 单个叶片静止状态下的各阶固有频率Table 1 Natural frequencies of a single blade in the static situation

4 试验验证

4.1 试验方案设计

模拟转子叶尖振幅与叶根动应变标定试验在中国航发四川燃气涡轮研究院临界转速试验器上开展，试验方案如图3所示。试验过程中，利用叶尖定时的非接触振动测试系统对转子叶片振动进行实时监测，利用动应变测试系统对叶根动应变进行测试。

图3 试验方案框图Fig.3 Block diagram of the testing program

根据叶片坎贝尔图分析结果及CFF 算法需要，在模拟转子对应位置安装了5 支光纤传感器，安装角度分别为0°、18.8°、38.0°、55.8°、270.8°。在1～5号每个叶片一弯振动模态下应力最大点粘贴电阻应变片，粘贴位置如图4(a)所示。结合滑环引电器实现转子叶片应变信号传输，采用动应变测试系统对应变进行测试与分析。非接触振动测试系统和动应变测试系统的转速基准实现方法均为：在模拟转子轴端喷涂1 道黑体漆，利用光纤传感器感应黑体漆和转轴其他部分到达时形成的电压信号获取1 转1个脉冲的转速基准。图4(b)为试验现场照片。

图4 应变片粘贴与模拟转子安装图Fig.4 Picture of the installation of strain gage and rotor blades

4.2 试验过程及结果

为了对比不同升速速率对试验结果的影响，试验验证过程中共进行了两次试验。第一次试验，试验件转速设置为：起动到5 000 r/min 后，以50 r/s 的升速速率上升到15 000 r/min，保持5 s之后，以50 r/s的降速速率下降至3 000 r/min，停留30 s后停车。第二次试验，调整升速速率及降速速率为30 r/s，重复第一次试验的步骤。试验件运转过程中，利用非接触振动测试系统实时监测模拟转子各叶片在不同转速下的叶尖振幅。离线处理时，利用SDOF和CFF两种算法可以准确获取标记叶片共振幅值、共振转速、共振频率以及激励阶次。利用动应变测试系统对应变片结果进行监测，对叶根动应变进行频谱分析。

试验过程中，上述两种测试系统监测结果显示：模拟转子5 片叶片均在约6 000 r/min、9 400 r/min、13 000 r/min发生6阶、4阶和3阶激励激起的一弯共振现象，且两次试验过程中数据重复性较好。

5 结果分析

5.1 频率误差分析

采用CFF 算法处理叶尖振幅数据，采用阶次谱分析方法处理叶根动应变数据。表2为各共振转速下非接触振动测试系统与动应变测试系统测得的叶片共振频率。表中，f1为非接触振动测试系统所得叶片共振频率；f2为动应变测试系统所得叶片共振频率；Re1表示评估非接触振动测试结果精度的相对误差，根据公式(9)计算。

从表2可看出：试验件转速6 000 r/min左右时，5片叶片均发生6阶激起的一弯共振，非接触振动测试系统与应变片测试结果的相对误差较小，最大为0.55%；转速9 400 r/min左右时，5片叶片均发生4阶激起的一弯共振，非接触振动测试系统与应变片测试结果的相对误差最大为0.28%；转速13 000 r/min左右时，5 片叶片均发生3 阶激起的一弯共振，非接触振动测试系统与应变片测试结果的相对误差最大为0.42%。总体上看，非接触振动测试系统与应变片测试结果的相对误差最大不超过0.55%。此外，升、降速速率30 r/s时的频率相对误差相较于升、降速速率50 r/s的小，且转速上升过程中的频率相对误差大于转速下降过程中的频率相对误差。

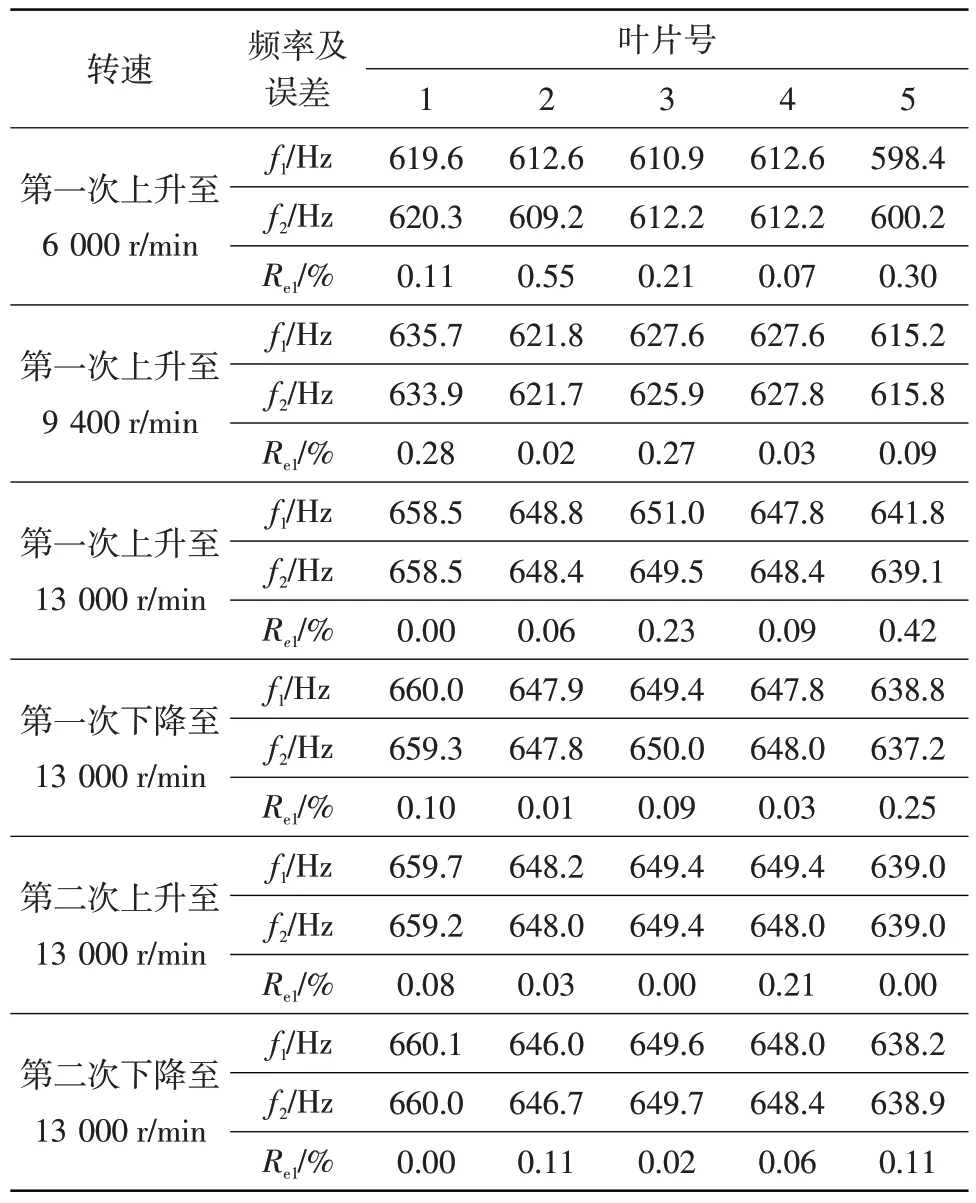
表2 叶片共振频率及相对误差结果Table 2 Blade resonant frequency and frequency error results

5.2 叶尖振幅与叶根动应变之比的误差分析

5.2.1 所有叶片试验结果求平均分析

利用公式(10)～(12)对测量的叶尖振幅与叶根动应变之比进行误差分析。

式中：ri为非接触振动测试系统测得的第i个叶片(i=1,…,5)叶尖振幅Ai与应变片测得的第i个叶片动应变峰值Ei的比值，ˉri1为ri的平均值，Re2为叶根动应变与叶尖振幅比值和平均值的相对误差。

根据上述模态分析基本理论可知，叶片发生一弯振动时，叶根最大动应变与叶尖振幅成一定比例关系。试验件转速为6 000 r/min、9 400 r/min 和13 000 r/min时，叶片均呈现单模态一弯振动。在各共振转速下，叶尖振幅、叶根最大动应变及Re2如表3所示。可以看出，试验件以50 r/s 速率升速至6 000 r/min 和9 400 r/min 时及降速至13 000 r/min 时，各叶片Re2均小于10.00%；升速至13 000 r/min 时，2 号叶片的Re2为14.40%，其余叶片的Re2最大为8.01%。试验件以30 r/s 速率升速至6 000 r/min 和9 400 r/min时以及降速至13 000 r/min时，各叶片Re2均小于10.00%；升速至13 000 r/min 时，2 号叶片的Re2为10.80%，其余叶片的Re2最大为6.84%。据此可知，模拟转子叶片在不同转速下发生一弯共振时，Re2在不同转速下不同，随试验件共振转速的升高而增大。原因为不同共振转速下，叶片离心力不同，造成Re2略有差异。升速速率为30 r/s的Re2比升速速率为50 r/s的小，且转速上升过程中的Re2较转速下降过程中的大。原因可能为转速上升过程中，叶片的整体气动负荷相对较大，对叶片的振动状态影响较大。

表3 叶尖振幅、叶根动应变及Re2分析结果Table 3 The results of the tip displacement and dynamic strain and Re2

5.2.2 单个叶片试验结果求平均分析

从表2 可知，由于加工误差等原因导致5 个叶片的动频出现差异，进而引起叶片振动特性的差别，不同叶片在同一转速下的叶尖振幅与叶根动应变之比也有一定区别。对于真实发动机的转子叶片，这种加工误差引起的叶片振动特性差异更为明显。为此，借助公式(13)对每个叶片在不同试验状态、同一转速下的叶尖振幅与叶根动应变的比值进行对比分析，结果见表4。从表中可以看出，在转速13 000 r/min时，2号叶片的Re3最大，为9.9%。