井中激发、接收的瞬变电磁深层精细勘探方法

沈建国,王春启,沈永进

(1.天津大学微电子学院,天津300072;2.北京华晖探测科技股份有限公司,北京101300)

瞬变电磁勘探通常在地面发射和接收(发射和接收线圈的垂直源距为0),或者在地面发射井中接收[1]。通常情况下发射线圈越大,激发的功率越强,探测的区域和深度越深[2-3],应用效果越好[4-6]。

随着人们对深部地层勘探的需求不断增加,在现有勘探原理的基础上提出了油井二次开发、剩余油分布研究、几何因子浅层勘探等方法[7-11]。因激发和接收点距离所测量地层较远,信号弱,故制约勘探效果的因素较多。

本文利用全空间瞬变电磁响应进行深层勘探,具体阐述如下:根据套管井地层电导率测量原理,将瞬变电磁发射源(线圈或电极)置于井底,将等间距阵列接收线圈或电极置于发射井内和相邻的接收井内,记录瞬变电磁场在地层中的响应过程,利用井中不同位置接收到的响应波形得到井底以下深部地层的电导率分布情况。

如果能够通过本井和邻井已经获得的测井曲线,将阵列接收波形中已知地层的特征去掉,便可利用线圈或电极激发的瞬变电磁场在全空间各个方向向外传播、扩散的动态过程,提取不同时刻波形所携带的深部地层电导率及其界面信息,实现电阻率的精细探测。

为此,将通过套管井节箍处的瞬变电磁响应得到套管井的几何因子[12],在裸眼井的响应中采用相减的方法去除直接耦合响应[13]。根据Doll电流环模型得到井间瞬变电磁涡流激发响应的全空间几何因子[14],进行模型实验[15],测量得到了不同空间位置的瞬变响应波形。井中空间小,在其中进行瞬变电磁激发,主要能量均可进入地层,因此激发的深部地层有用信号较强,受影响的因素较少。

本文利用瞬变电磁满足的基本方程及其解析解计算瞬变电磁响应波形,从相位变化反映瞬变电磁能量空间传播情况的角度分析瞬变电磁响应波形的特点,对比线圈激发和电极激发的响应波形,分析波形中界面信息的分布方式,并且利用一维模型展现电导率界面的瞬变电磁响应波形。根据电磁感应原理研究电极激发的响应波形以及与地层电导率直接相关的涡流再次激发响应。响应波形每一时刻的幅度都包含距离激发源一定深度地层的涡流再次激发响应,并与该深度地层的电导率成正比,直接指示该地层电导率。不同时刻套管井测井波形的幅度与裸眼井电导率测井曲线的一致性验证了上述结论。

1 全空间瞬变电磁响应的幅度、相位与电导率

任何瞬变电磁响应均可以视为正弦激励e-iωt响应的叠加。无论是电极还是线圈,其在全空间(无限大均匀地层)中激发的瞬变电磁场均按照推迟势reiγr/r向外扩散、传播。其中,(地震波)电磁波(电导率为0或者高频)的响应反映了其传播过程,速度v为常数,不同位置的响应波形形状一样。瞬变电磁势函数A在球坐标系下可表示为:

(1)

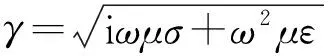
(2)

(2)式所描述的瞬变电磁A既有相位移动又有幅值衰减,幅值衰减和相位移动均随频率改变,且衰减剧烈,因此导致不同源距的响应波形完全不同。如图1a 所示,该响应为点源激发的响应(格林函数),用于描述导电介质中瞬变电磁场的传播特征,响应特征与激发源类型(线圈、电极)无关,为瞬变电磁场在无限大均匀介质中传播后的响应特征。波形的上升沿包含了丰富的地层信息,但是对于这样的波形,人们很少从瞬变电磁能量传播(扩散)的角度对其相位信息及其波形上的延迟进行分析。在套管井地层电导率测井和井底瞬变电磁精细勘探中,瞬变电磁能量的传播(扩散)展现了响应时间与地层深度之间的对应关系,有助于我们从不同时刻的响应中获得不同深度的地层电导率,因此有必要对波形形状、延迟以及对应的空间分布进行分析。

将图1a中不同源距的响应波形放大不同倍数后绘制在一起得到图1b,从图1b中可以看出,不同源距的瞬变电磁响应均具有非常明显的延迟(传播特征),具体表现为:不同源距的响应起始点、上升沿和峰值等均有明显的时间差。波形中起始点、上升沿和峰值所在的3个时刻及其对应响应形状反映了瞬变电磁响应的主要特征。图1a中响应波形的时间差所反映的传播过程与电磁波和地震波的传播过程完全不同:不同源距的响应波形差异大,并且这些差异存在于波形的各个时刻。这个差异使得我们无法像处理地震波和电磁波那样,根据相位一致的原则从测量的波形上求取时间,也无法用响应波形的(单个)延迟时间来描述传播过程。这是瞬变电磁场与电磁波场传播的根本区别。

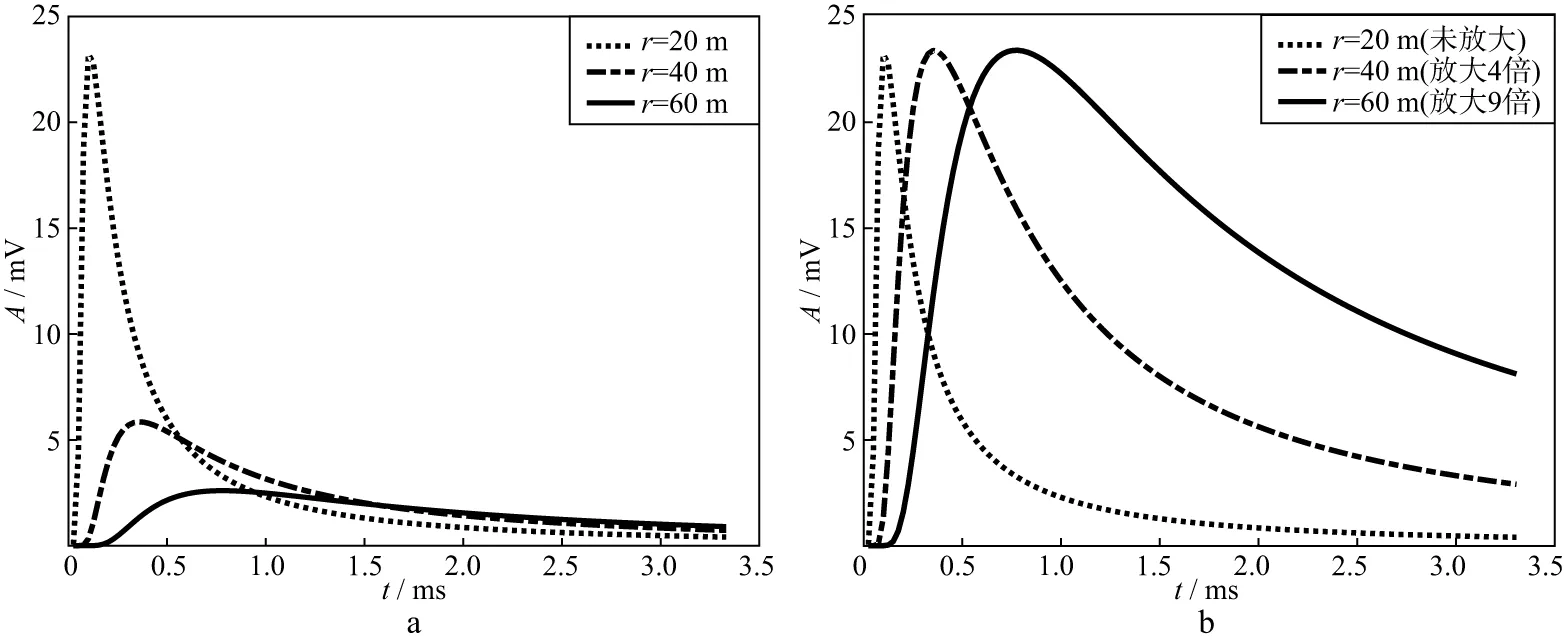
图1 点源在无限大均匀介质中激发得到的不同源距的响应波形(a)以及放大以后的响应波形(b)

由(2)式可知,瞬变电磁能量经过一定的距离传播后,因不同频率的响应延迟时间(不是一个常数)[16]和幅度衰减均不同,故所有频率的响应叠加后形成的响应波形形状不同。

图1b中的时间差异由(2)式中指数的虚部(第2项)决定,相位移动作为影响瞬变电磁响应的第2个因素,随频率和电导率变化,并可折算为延迟时间t0:

(3)

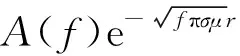
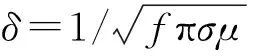
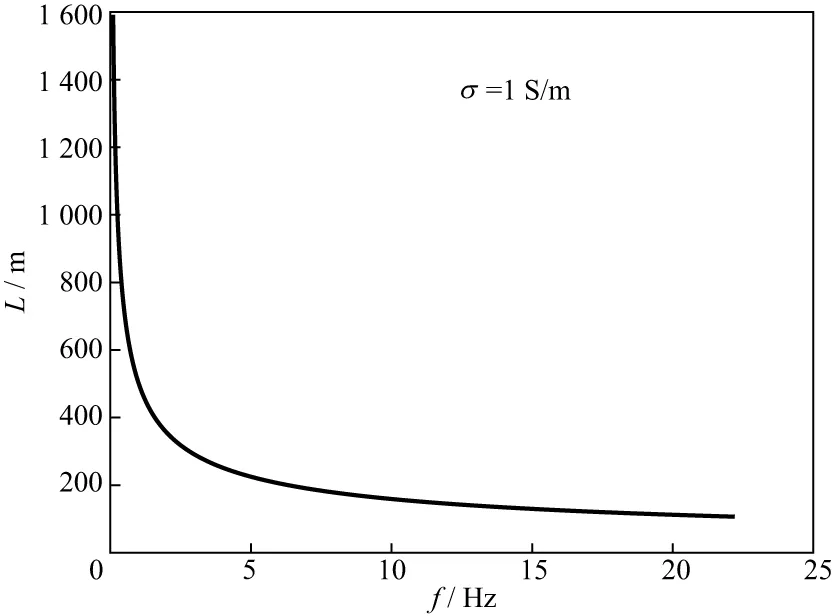
图2 电导率为1S/m的地层集肤深度随频率变化的规律

在裸眼井中激发瞬变电磁场,通过井内的阵列接收线圈或电极接收不同源距的瞬变电磁响应。频率越低对应的集肤深度越大,瞬变电磁能量能够到达的地层深度越深,波形变化越慢,这些深层的信息在瞬变电磁响应的后续波形中有所反应。

2 不同源距波形的延迟时间与传播速度

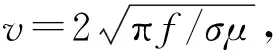
图3为线圈在无限大均匀介质中4个不同源距下激发的瞬变电磁响应(实线、短虚线)及响应差(长虚线)。图3a是电导率为1S/m时,冲击函数激发,源距2m处的响应波形,其延迟时间小于0.5μs,波形上升快(高频成分丰富)、下降慢且拖尾(高频成分部分衰减,幅度减小导致),与冲击函数的形状(上升、下降均极快)不一样。因为延迟时间太短,在近源距通过测量延迟时间获得地层电导率需要进行难度较大的高速模数转换器采集。图3b、图3c和图3d分别为:传播10m时延迟时间接近4μs的响应波形,传播20m时延迟时间约20μs的响应波形,传播40m时延迟时间达到60μs的响应波形,即源距越长,响应起始时刻的延迟时间越长。这是因为源距越长,频率成分衰减越多;频率越高、衰减越大,高频的成分衰减较多;剩余的低频成分传播速度慢,传播延迟时间长。波形幅度起始时间(响应为零的时间长度)随着源距的增加呈非线性增加。无论延迟多长,响应波形均呈现快速上升达到峰值,而后缓慢下降的形态。因不同源距的波形差异很大,故不能像地震波那样进行相关对比和分析,只能根据波形的特点研究其它信号的处理方式。

图3 线圈在无限大均匀介质中4个不同源距下激发的瞬变电磁响应及响应差a r=2m; b r=10m; c r=20m; d r=40m

3 线圈激发的响应及有用信号

根据电磁感应原理,线圈激发的瞬变电磁响应随时间变化,在地层中激发的感应电场是闭合的,会产生随时间变化的涡流并再次激发响应即二次场响应。因为涡流与地层电导率成正比,故其激发的响应也与地层电导率成正比,并混叠在瞬变电磁响应中。提取实际测量波形中涡流再次激发的响应,可以用于研究地层的电导率及其空间分布情况。因此,这种再次激发的响应为有用信号。

DOLL采用假设的地层电流环模型研究了发射线圈激发的涡流及其在接收线圈产生的二次场响应,得到了发射、接收线圈之间的直接耦合响应和涡流再次激发的二次场响应表达式。对于线圈系结构而言,其直接耦合响应也是确定的,因地层电导率不同导致涡流激发二次场响应存在差异。将同一源距下不同地层电导率对应的响应相减,可消除直接耦合响应,得到涡流再次激发响应的差,即不同地层涡流引起的响应差[18-23]。在响应变化最快的位置,响应差出现峰值(图3)。上述结论符合电磁感应定律:涡流激发的二次场响应与涡流在接收线圈引起的磁通量随与时间的变化率成正比(涡流引起的磁通量与瞬变电磁响应成正比)。因此,涡流激发的二次场响应与瞬变电磁响应对时间的导数成正比,此处的瞬变电磁响应对应地层(内部)的响应,涡流激发的二次场响应与地层电导率成正比。

瞬变电磁响应中涡流激发的二次场响应对于理解响应波形中的有用信号具有重要意义。响应波形是随时间变化的,在不同时刻有不同的响应幅度。这些响应幅度包含怎样的有用信号?与哪个深度的地层电导率有对应关系?

图3中各个源距的响应差峰值所在时刻是激发源在该深度位置地层电导率产生最大涡流激发信号的时刻,涡流再次激发的二次场响应(涡流到接收线圈的传播时间很短)直接叠加在此刻的原始响应波形中(与瞬变电磁响应信号相比很小),或者说此时测量的波形值包含直接反映该深度位置的涡流激发的二次场响应。此时该深度地层的电导率产生的涡流激发响应最大,所有源距的响应中该时刻的响应值集中反映了该深度地层的电导率。其它深度的地层产生的涡流因为随时间变化慢,因此激发的响应较小。当该深度的响应达到峰值,对时间的导数为0时,其涡流激发的二次场响应为零。

随着时间推移,该深度位置的响应(达到极值后)开始下降,对时间的导数为负值,其涡流值激发的二次场响应信号为负值,叠加在后续的响应波形中。因响应下降慢,对时间的导数小,故此时该深度位置涡流激发的二次场响应小。此时瞬变电磁能量传播到较深位置的地层,有些位置的响应刚刚开始上升,涡流开始增加,有些位置的响应早已上升,上述响应对时间的导数均为正,涡流激发的正二次场响应叠加在该时刻的响应波形中。在上升最快的深度(地层)位置,地层电导率对涡流激发的二次场响应的贡献最大,该时刻的波形值主要用于测量该地层的电导率。

综上所述,在所有源距的响应波形中,每个时刻的响应值均对应于距离激发源某个深度的地层区域的响应,该区域瞬变电磁响应上升最快时,产生的涡流对时间的导数最大,其电导率产生的涡流激发出最大的正二次场响应。对于每个地层激发深度而言,较其浅的地层产生的涡流对时间的导数较小,当导数为负时,涡流激发出负的二次场响应,较其深的各个地层响应开始增加,但因响应幅度较小,故产生的涡流较小,变化较慢,涡流激发的正向二次场响应也较小,这些与地层电导率成正比的二次场响应均叠加在瞬变电磁响应波形中。

所有不同源距的响应波形同一时刻的幅度值均对应距离激发源同一深度位置的地层。该地层为此刻的波形提供最大的涡流激发响应,比其更深的地层提供的响应幅度较小,比其更浅的地层则提供负的涡流激发响应。当浅部地层涡流二次激发的负响应幅度超过较深地层涡流二次激发的正响应幅度时,总的涡流二次激发的响应为负,并且随着时间的增加逐渐减小。

以上结论适用于地层和井中任意位置的瞬变电磁响应。瞬变电磁响应变化时刻即为接收线圈接收到的涡流激发二次场响应的时刻。

4 电极激发的响应及其有用信号

根据电磁感应原理,点电极或棒状电极激发的瞬变电磁响应在地层中也产生涡流,这种涡流与线圈激发的涡流存在差异。电极激发的瞬变电磁场与线圈激发的瞬变电磁场空间分布相互垂直,因此,在柱坐标系下,线圈激发的磁场沿半径和轴线z方向分布,电场沿圆周方向形成闭合的圆环;电极激发的电场沿半径和轴线z方向分布,磁场沿圆周方向形成闭合的圆环。电极激发的瞬变电磁响应中,电场呈现放射状,激发的涡流沿半径和井轴z方向呈放射状辐射至无穷远,其产生的磁场沿圆周方向分布。因为该磁场随时间变化,故其在接收电极位置同样会再次激发电响应,该响应与地层(圆球形状)电导率有关。图4为不同源距下点电极激发的瞬变电磁响应及响应差,其响应形状与图3相似:先快速上升达到峰值以后再慢速下降。具体的差别表现为图3中两个不同地层电导率的响应差在响应变化最快的位置出现极大值之后快速减小,最后为很小的负值。在电极激发的响应中,距离激发电极某个深度地层的涡流激发的二次场响应在某个确定的时刻(其响应变化最快、即上升最快)最强,周围其它地层响应变化比较慢,涡流激发的二次场响应幅度较小。此时距离激发电极较近的地层响应开始减小,其地层涡流在响应减小过程中二次激发的响应为负。因为响应减小时变化比较慢(拖尾),故其地层涡流二次激发的响应幅度小。距离激发电极较远的地层此时开始有响应,且响应幅度逐渐增加,其涡流激发的响应为正。随着时间的增加,响应变化最快的地层其涡流激发的二次场响应逐渐减弱为零并转换极性,而距激发源较远处的地层涡流激发的二次场响应开始达到极大值。在每个时刻,所有地层涡流激发的二次场响应均叠加在实际测量的响应波形上。每个时刻的响应波形中均包含该时刻瞬变电磁场扩散(涉及)到的全部空间的涡流激发响应。由于激发电极周围介质的响应始终存在,每个时刻的响应均在变化,因此空间每一点的响应波形中均包含其涡流激发响应。利用后续响应中的涡流再次激发响应获取较远或者深部地层的电导率时,需要将电极近处地层的涡流激发响应从波形中去除。

图4 不同源距下点电极激发瞬变电磁响应及响应差a r=2m; b r=10m; c r=20m; d r=40m

当线圈和电极分别激发出瞬变电磁场后,由于电场强度和磁场强度均随时间变化,根据Maxwell方程的两个旋度公式可知,瞬变电磁场在空间的分布也是变化的,不会在空间中停留,也不会像直流电磁场那样在空间各点形成一个稳定的分布(不随时间变化),而是在不同时刻分布在不同的空间中。

图5a和图5b是线圈激发的瞬变电磁场在0.10ms和0.12ms的空间分布情况,随着时间的增加,瞬变电磁场分布区域逐渐扩大,向外传播特征明显。但当瞬变电磁能量达到一定区域后,由于地层电导率引起的衰减和相位移动,导致瞬变电磁能量在向外传播的过程中较高的频率成分幅度衰减得很快,随着时间的推移,瞬变电磁场的主要能量仍然集中在发射源附近的一定区域内(地震波或者电磁可以集中能量一起向外传播)。由于不同频率的瞬变电磁能量经过了不同程度的衰减(集肤深度),到达一定的区域时,幅度均已减小,经过相移再叠加,幅度均较小。从图5c和图5d可以看出,随着时间的增加,中垂线区域内的瞬变电磁幅度开始逐渐减小,最终消失在近源距的某个区域内。

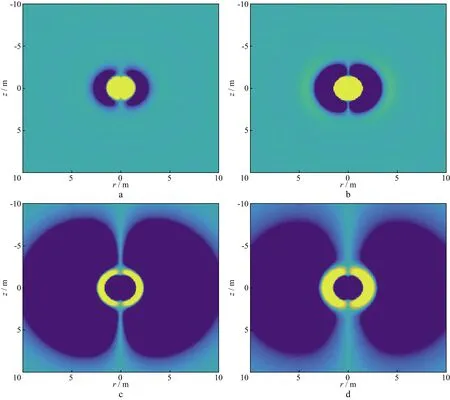
图5 线圈激发的瞬变磁场在0.10ms(a)、0.12ms(b)、0.68ms(c)、0.82ms(d)时刻的分布情况

在图5的瞬变电磁响应空间分布的等势面(球形)上,每一点均具有相同的响应波形和涡流。该分布区域(各个轮廓线)中的瞬变电磁能量随时间变化存在差异,某个时刻,瞬变电磁能量变化最快的区域(轮廓线)即为波形中该时刻所测量的区域。这些区域内随时间变化的涡流均会在接收线圈上再次激发响应,区域内每一点涡流再次激发响应的贡献与接收线圈所在的空间位置有关,可以用空间几何因子对其进行描述[14]。

5 电导率界面的响应

由于瞬变电磁场在界面的响应对地下勘探具有重要意义,因此从实际测量的波形中分离出界面的响应即可确定界面的存在,也可进一步确定另外一个地层的电导率。

我们采用一维介质模型正弦激励eiωt对电导率界面的影响进行研究。忽略介电常数项,一维瞬变电磁场满足的微分方程:

(4)

(5)

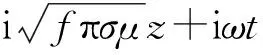
一维两层模型如图6所示,假设两层介质的电导率分别为σ1、σ2,磁导率μ相同。在左边的介质有激发源,激发瞬变电磁(R)场入射到边界,遇到边界后发生反射(F)和透射(T),反射场包含地层界面信息和第二层的地层电导率信息。

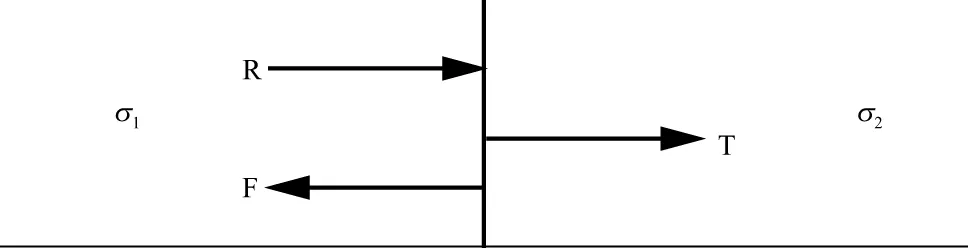
图6 介质电导率不同的一维两层模型

为具体展示一维两层模型中反射波的形状和特征,将坐标原点取在图6所示的两层介质交界位置,并假设左边第一层电导率σ1为100S/m,相对磁导率为1,第二层的电导率σ2为90S/m,相对磁导率为1,取频率步长df=0.01Hz;激发源到界面的距离为140m,第一层的接收点到界面的距离为10m,第二层的接收点到界面的距离为20m。图7中红线是瞬变电磁场经过第一层的接收点时的响应波形,黑线是从界面反射后反射场到达接收点时的响应波形(放大10倍),绿线是接收点实际接收到的全波波形。将反射场继续放大得到图7b,可以看出:反射场较入射场有明显的延迟,该延迟为入射场经过接收点到达界面后,从界面反射再次传播到接收点所经过的时间。在此过程中,反射场经过了20m的衰减和一次反射,因此其波形不但延迟而且形状与入射场相比还存在较大的变化(变缓)。此波形与入射场叠加后,对接收波形会产生一定的影响(如图7中红线与绿线之间的差别)。因影响较小,并未像地震波那样构成独立的反射波(地震的反射波是独立存在的,在时间上与入射波分离),而是界面引起的反射场与幅度较大的入场波同时存在于同一时间段内,其影响贯穿于整个响应波形中。

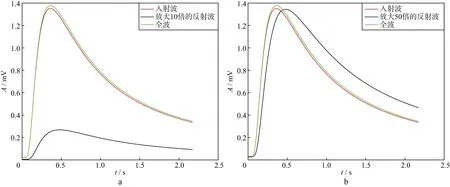
图7 两层介质模型反射波放大10倍(a)以及反射波放大50倍(b)后的入射波和反射波以及全波波形

6 分析与讨论

利用井中激发瞬变电磁场,并在井内一定的源距(区域)以外沿井轴方向进行阵列接收,瞬变电磁场经过接收阵列时会出现响应波形先快速增加达到极值,之后再缓慢减小的变化过程。不论是线圈还是电极激发,不同位置的响应波形均具有这样的形状。利用该波形形状进行深部地层及界面勘探,必须先清楚其中的地层电导率信息分布方式,地层电导率以3种形式存在于阵列接收的响应波形中,具体阐述如下。

1) 响应波形的幅度。沿一定的方向阵列接收到的每个频率的波形幅度均是按照1/r乘以指数规律衰减的,其指数衰减系数与地层电导率的开方呈线性关系。通过求取不同源距接收到的各个频率的波形幅度的指数衰减系数可以获得地层电导率。

2) 响应波形的相位。沿一定方向阵列接收到的每个频率的波形相位随源距呈线性变化,其斜率与地层电导率的开平方成正比。获得各个频率的相位随源距变化的斜率即可获得地层的电导率。

3) 根据电磁感应原理,瞬变电磁响应在地层中会产生涡流,涡流随时间改变会再次激发新的响应,该响应与地层的电导率成正比。地层响应变化最快的时刻涡流激发的二次场响应最大。瞬变电磁响应波形的每个时刻均对应某个深度的地层,响应值集中反映该深度地层的电导率。

利用响应波形的幅度和相位获得的地层电导率随频率改变,频率越低,探测的深度越深,涉及的地层区域越大。根据不同频率的电导率构建一个深度剖面,在已知频率与深度的对应关系(可以用集肤深度)的情况下,可以获得地层电导率由浅入深的变化情况。两种方法均是对整个波形进行处理,是整个波形中不同时刻所包含的地层电导率的综合提取方法。

利用瞬变电磁场的扩散过程和瞬态特征,将不同时刻的响应与距离激发源的深度对应,即可得到响应波形中不同时刻包含的地层电导率信息,该方法的有效性在套管井中得到了验证。提取套管井中实际测量的瞬变电磁响应波形在10个时刻的幅度(对应于10个径向深度地层的电导率),并按照测井深度与裸眼井所测量的电导率曲线(RT)综合绘制,结果如图8 所示。图中黑线是裸眼井测量的电导率曲线,彩色的10条线分别是10个时刻井内瞬变电磁测量波形的幅度,两者的深度存在1m的偏差(黑线向右移动了1m)。右边的曲线形状非常相似(左边的差异是地层扩径所致)。原始测量波形的幅度与地层电导率相关,反映了地层电导率的变化。

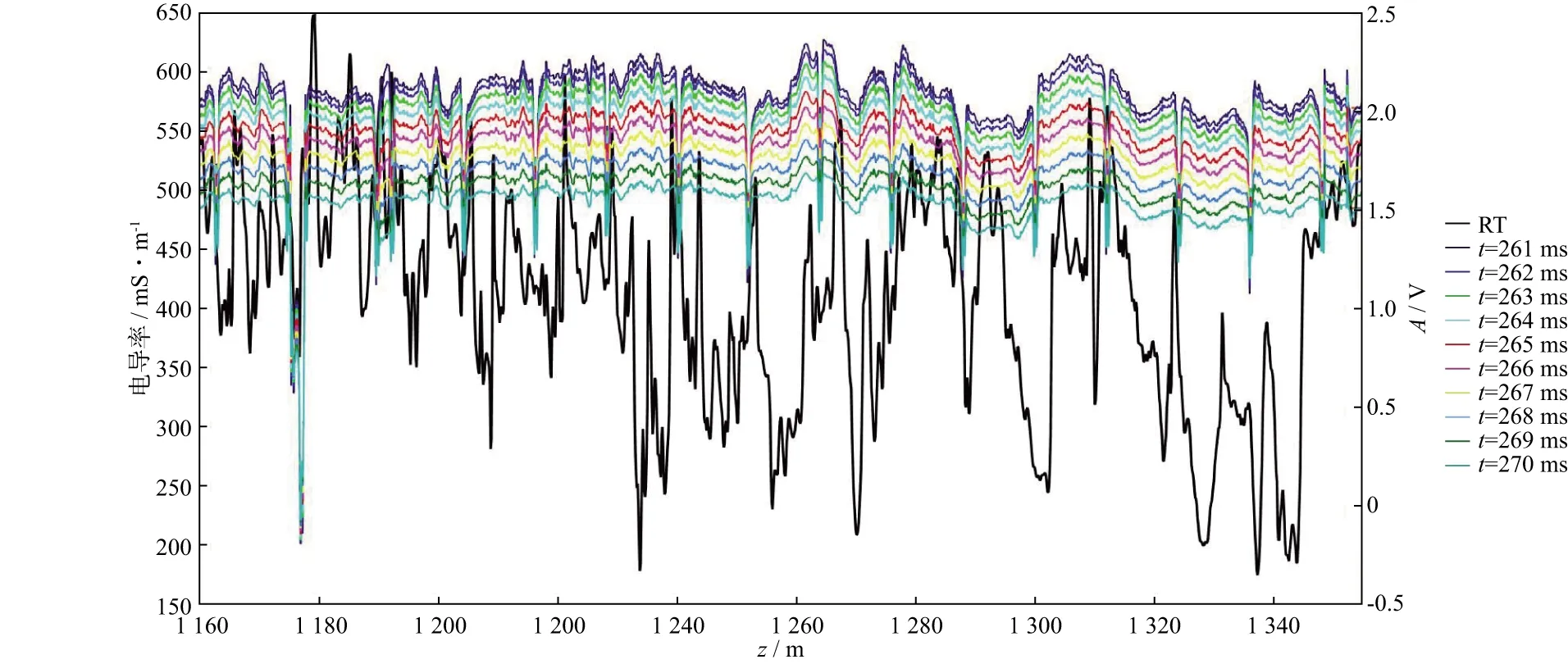
图8 套管井瞬变电磁测井波形10个时刻的幅度随深度的变化情况及感应测井电导率曲线

地层电导率界面产生的反射波,直接反映了界面的存在。反射场与入射场叠加在一起贯穿于整个响应波形中。当电导率差异较小时,反射波的幅度也较小。

7 结论

利用井中激发、阵列接收瞬变电磁响应波形频谱的幅度、相位以及涡流再次激发的响应均可获得不同深度地层的电导率,根据响应波形的形状还可以获得不同深度电导率界面。波形中每个时刻的幅度与距离激发源的某个深度地层的电导率对应,即在波形上取某个时刻,此刻某个与其对应的区域(距离激发源某个深度)地层响应变化最快,其涡流在每个位置激发的二次场响应最大。电极和线圈激发均能产生与地层电导率成比例的二次场响应。地层涡流激发的二次场响应在其响应(涡流)增加时为正、减小时为负,波形中的二次场响应是各个地层所激发的不同极性的二次场响应的叠加。界面反射产生的响应与瞬变电磁响应叠加在一起,贯穿于后续的响应波形中。线圈激发的瞬变电磁场以偶极子波阵面的形状扩散,其上各点的涡流相同,均在接收线圈再次激发二次场(受空间位置影响),该二次场是波形中的有用信号,也是精细勘探的理论基础。由于瞬变电磁响应的二次场幅度比较小,响应中与地层电导率无关的直接耦合响应幅度较大,故需要进一步研究去除直接耦合响应的方法。