基于延迟时差的陆地双检地震数据评价方法

李安昱,尤加春,刘学伟,韩文功,张光德,杨德宽

(1.中国地质大学(北京)地球物理与信息技术学院,北京100083;2.成都理工大学地球物理学院,四川成都610059;3.中国石化石油工程地球物理有限公司,北京100728;4.中国石化石油工程地球物理有限公司胜利分公司,山东东营257086)

近年来,为满足岩性勘探的需要,保幅偏移技术成为地震资料处理中成像技术的热点之一。目前主流保幅偏移方法大致可分为射线类保幅偏移方法、单程波真振幅偏移方法和逆时偏移方法三大类。传统射线类保幅偏移算法对射线积分算子加权实现保幅,该类算法对于复杂构造成像的能力有限[1-2]。单程波真振幅偏移算法对常规单程波算子加入一定的振幅修正项以实现保幅,但单程波本身是对全声波方程的近似,导致横向变速较大时对大角度构造的成像效果较差[3-5]。逆时偏移算法理论上能处理波在任意速度变化介质中的传播问题,但存在低频噪声、多次波虚假成像和计算量大的缺点[6-7]。目前的保幅偏移方法在解决岩性勘探的难题时依然受诸多限制,射线类和单程波保幅方法虽然一定程度上提高了振幅保真能力,但该类方法解决复杂构造保幅成像的能力偏弱,工业应用的性价比较低。逆时偏移对计算机硬件性能要求较高,尽管发展了多种加速方法,仍然不能广泛应用于工业生产[8-9]。从偏微分方程数值求解的角度分析,声波方程是一个关于时间和空间变量的二阶偏导数微分方程,理论上在深度域或时间域求解需要两个边界条件方可准确求解。

2016年,YOU等[10]从求解波动方程出发,发现了求解全波动方程的双检偏移方法有更好的保幅性。2017年,YOU等[11]提出了逆时外推的双检波器逆时偏移算法,并通过数值实验证明了该算法相比于传统逆时偏移方法能提供更加精细的构造成像和更加准确的振幅计算。2018年,YOU等[12]提出了地震数据双检采集系统,将采集到的双层数据作为初始条件,发展了一种基于单程波传播算子的双程波深度偏移算法,并通过数值试验证明了该偏移算法比单程波成像算法具备更大角度的成像能力。孙幸未[13]分析了检波器一致性、地质构造复杂度和速度误差对双检深度保幅偏移方法的影响,得出速度误差对保幅性影响较大的结论。赵庆伟[14]对双检数据的成像方法进行了系统的对比分析,证明了双检成像在保幅性上比单程波成像更具有优势。ZHONG等[15]发展了基于双检采集系统的矢量声波方程全波形反演方法,相比于传统方法,该方法提高了反演的精度,并具备更好的收敛性。与陆地双检不同,海上双检利用水、陆检波器极性差异消除鬼波。张振波等[16]利用海上双检上下缆地震数据联合处理,改善了深层弱信号成像效果。李洪建等[17]将最小二乘反演和匹配滤波算法引入海上双检数据的合并处理,进一步提高了鬼波压制效果并拓宽了资料频带。

双检深度偏移算法应用于理论数据优势明显,能适应任意方向的速度变化和复杂构造的真振幅计算,算法易于编程实现,计算效率较高,而且已具有相应的采集技术和设备,具备工业生产的潜力和条件。但在实际数据采集或处理中,由于施工、检波器耦合或后期处理不合理等因素造成了上下层检波器间的延迟时差不能达到预期的质量,使得成像效果不理想。因此,必须建立陆地双检地震数据的评价方法以满足全声波方程保幅偏移计算的要求。

针对陆地双检采集系统的需求,我们建立了基于延迟时差的陆地双检数据质量评价方法,以指导实际数据的采集和处理,保证成像输入数据的有效性,对陆地双检地震勘探方法的工业化应用具有重要的意义。

1 延迟时差对成像的影响分析

1.1 基本原理

在二维情况下,基于双检波器地震数据采集系统的全声波方程边值问题可写为:

(1)

式中:u(x,z,t)是地震波位移场值;c(x,z)是介质速度模型;Δz是深度方向的网格剖分;d(x,z=0,t)和d(x,z=Δz,t)分别是双检波器采集系统在z=0和z=Δz处采集的地震数据,用这两个数据的一阶差商来计算地震波场对深度方向的导数值uz(x,z=0,t)。上述两个边界条件为在深度域求解声波方程提供了充足的理论依据。

为了便于求解该方程,对时间做傅里叶变换:

(2)

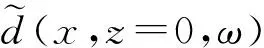
(3)

在频率-波数域对两个边界分别沿深度方向波场外推,外推算子可表示为:

(4)

式中:kx为水平波数;zi表示延拓至某深度处;“±”中“+”、“-”分别表示对检波器波场的反向外推和正向计算。传播算子的精度决定成像的质量,kz计算公式中角频率可表示为:

ω=2πf

(5)

式中:f为频率。

一般情况下,双检采集系统的层间间距为1m左右,相对于上千米的地下反射界面而言,这种检波器间的深度差所引起的波场传播路径差异,可近似为来自地下同一点处的反射,因而其理论延迟时差ΔT可近似为:

(6)

式中:Δz表示检波器层间深度差;v为表层速度。当理论延迟时差小于时间采样率时,即:

(7)

式中:T为时间采样间隔;fs为采样频率。两层数据之间的差异就不能被检波器分辨,在时间记录上表现为数据的重叠,在频域表现为同一频率成分下没有一定的相位差,所采集的这种双检数据没有意义。

因此,特定延迟时差是边界条件有效的保证和前提,也是评价双检数据最直观的指标。

1.2 模型数据分析

设计3层水平模型如图1所示,网格大小为601m×601m,网格间距为1m,采样间隔为0.2ms,采样时长为0.4s。震源位于模型x=300m,z=250m处,采用主频为45Hz的雷克子波。上层检波器位于z=250m处,下层检波器位于z=251m处,上、下层检波器间距为1m,道间距为1m,共601道接收。

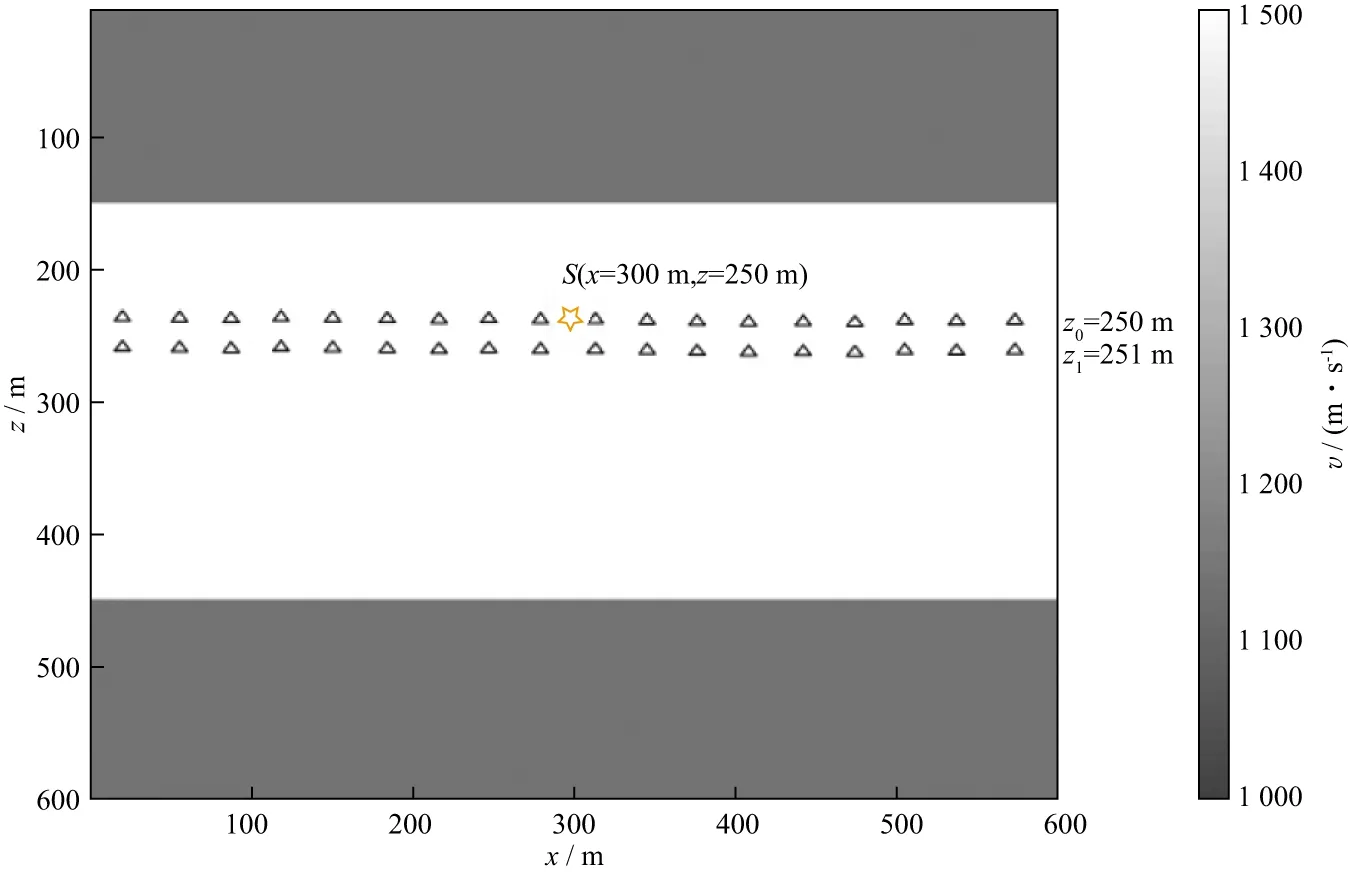
图1 双检正演速度模型

上、下层正演记录及波形示意如图2所示,由于检波器组距上边界距离较近,故正演记录中第一个反射波同相轴代表上边界的反射信号,第二个同相轴代表下边界的反射信号。上层检波器先接收到上边界反射信号,绿色框内蓝色虚线代表的上层检波器数据走时早于黑色线代表的下层检波器数据。同理,橙色框内走时关系正好相反。

图2 正演记录波形示意

用该正演单炮记录和速度模型z=250m以下的部分,分别进行常规单程波裂步傅里叶(SSF)法深度偏移和双检成像对比。成像结果如图3所示,其中图3a 为常规单程波SSF法偏移结果,图3b为双检偏移结果,图3c为上、下层时差关系反置后的双检偏移结果。分析图3可知,常规偏移只采用一个初值条件,求解完整波动方程时缺少边界条件,通常做法是舍弃一项分裂为单程波方程,成像时对检波器波场按照上行波处理,造成图3a中箭头所示处的虚假成像轴。双检偏移采用两个初值条件,可求解完整波动方程,利用双边界条件导出的双程波延拓方法进行波场外推,成像位置准确,如图3b所示。当走时关系相反时,双检成像误将来自上边界反射当作下边界处理,造成图3c 所示的错误成像位置。

图3 深度偏移成像剖面a 单程波SSF法深度偏移; b双检深度偏移; c 反向时差关系的双检深度偏移

改变延迟时差的稳定性,来探究其对双检成像的影响。该模型理论延迟时差为0.8ms,对下边界反射同相轴分别进行±0.4,±0.8,±1.6和±3.2ms 随机时移改变,延迟时差分布情况和成像剖面分别如图4a至图4b、图4c至图4d、图4e至图4f 和图4g至图4h所示,提取各成像剖面该反射界面的成像振幅对比如图4i所示。分析组图,当时差在较小范围内扰动时,构造成像和成像振幅基本不会受到影响。当延迟时差超出理论时差一倍以上浮动时,出现明显的成像噪声,随着延迟时差的进一步发散,成像振幅逐渐偏离理论反射系数,保幅性大大降低。

图4 不同延迟时差分布、相应的成像剖面及成像振幅对比a,b 改动范围为±0.4ms; c,d 改动范围为±0.8ms; e,f 改动范围为±1.6ms; g,h 改动范围为±3.2ms; i 成像振幅对比

综上所述,双检数据层间延迟时差对双检构造成像和保幅性均具有重要的意义,延迟时差的走时正反影响双检构造成像位置,正延迟时差的稳定性影响双检成像的保幅性。

2 双检数据评价方法

作为评价双检数据的重要指标,延迟时差的定量计算采用互相关法。

先求出上、下层对应单道数据xi(t)和yi(t)的互相关函数Rxy:

(8)

相关值最大时采样点位置记为RN,则其与单道采样点数W之差为相关延迟样点数,该数据延迟时差Td可表示为:

Td=(RN-W)*S

(9)

式中:S为时间采样率。

图5直观显示了上、下层数据单道波形和互相关曲线的对应关系。

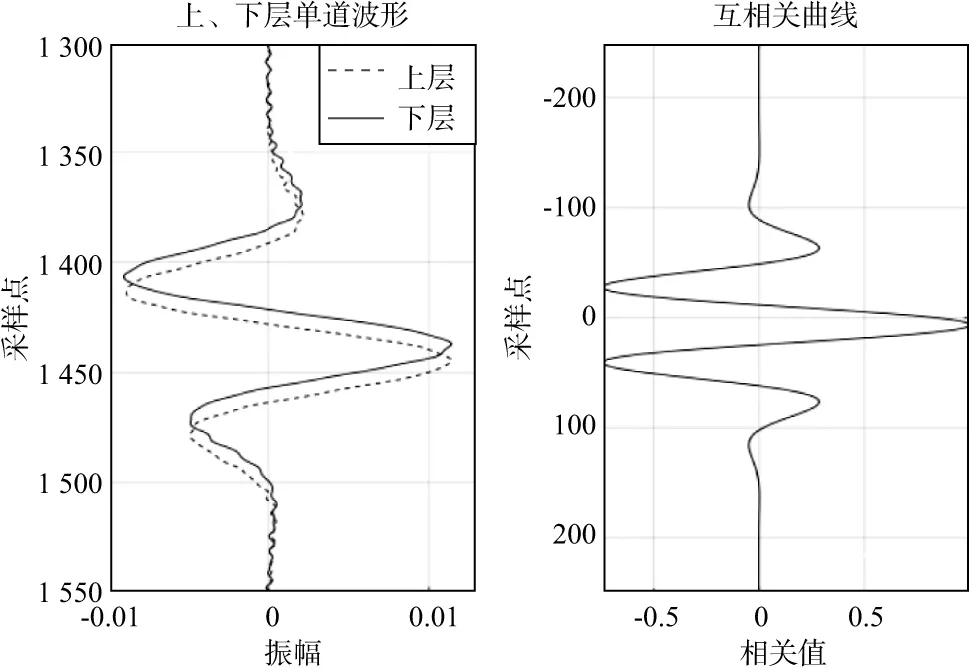
图5 双检数据上、下层单道波形及其互相关曲线

实际资料中,存在负值延迟时差或者明显偏离主分布轨迹的延迟时差,需设置合适的阈值予以剔除,剔除异常后的部分定义为正常延迟时差,求其平均值记为MTd:

(10)

式中:Tdj为第j道的延迟时差;X为有效道数量。

(11)

式中:xi(t)和yi(t)为上下层对应单道数据;N为单道采样点数;M为道数。

同样地,我们可以将上述层间求取延迟时差和振幅差的方法用于上层数据相邻道之间,以获取道间延迟时差和振幅差,计算方法同上。

基于上述计算方法,可获得层间和道间延迟时差及振幅差,层间和道间正常延迟时差占比6个指标的计算结果,结合时差对双检成像的影响分析,我们提出了基于延迟时差的双检数据评价函数:

(12)

式中:c=(0.6c1+0.2c2+0.2c3),c1为层间和道间延迟时差的相关系数,c2为层间和道间振幅差的相关系数,c3为层间和道间正常延迟时差占比的相关系数,c为上述3个相关系数的加权平均;l为层间正常延迟时差占比的均值;δ为各炮层间延迟时差的标准差。

评价函数值Y介于0～1,越接近1表示数据质量越好,越接近0则数据质量越差。

应用该评价函数评价大规模叠前数据时,应以单炮或炮段为单位,分别计算层间延迟时差、道间延迟时差、层间振幅差、道间振幅差、层间正常延迟时差占比和道间正常延迟时差占比6个指标,计算完成后,汇总各炮或炮段的各指标均值,再代入该评价函数定量计算。评价局部道或者单炮数据时,鉴于评价函数中的加权相关系数c计算方法本身局限于正态分布的假设条件,当延迟时差为定值时易导致标准差分母为零,可视具体情况舍弃该项进行评价。

3 实际应用

3.1 模型数据测试

设计4层层状水平模型,网格大小为1200m×2000m,网格剖分为2m×5m,道间距为10m,上、下检波器层间间距为2m,采样间隔为0.5ms,采样时长为3s,共200道接收。震源位于模型x=1000m,z=0处,雷克子波主频30Hz。采用多次覆盖观测系统,最小偏移距为0,炮点从第一个检波点开始布设,炮间距50m,共激发40炮。

正演记录中加入随机噪声,控制信噪比(RSN)分别为4,3,2时的模型数据和层间延迟时差分布如图6a至图6c所示,加入面波后如图6d所示,不同信噪比数据成像振幅对比如图6e所示。分析组图可知:

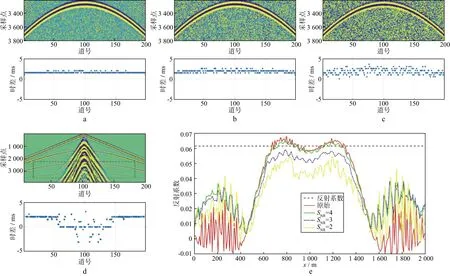
图6 模型数据测试a,b c 信噪比分别为4,3,2时的数据及延迟时差分布; d 面波及其延迟时差; e 各模型双检成像振幅对比

1) 纯反射波数据的层间延迟时差为2.0ms,不随偏移距和反射界面深度的变化而改变;

2) 随着信噪比降低,层间延迟时差呈现发散趋势,信噪比大于3时延迟时差基本接近理论值,信噪比小于3时则逐渐发散;

3) 在强能量面波存在区域,延迟时差接近于0;

4) 信噪比高于或接近于4时,成像振幅基本与理论反射系数吻合,信噪比低于3时成像振幅明显偏离理论反射系数。

应用评价函数分别评价各模型数据,评价结果如下:

纯反射波模型数据,时差为定值2.0ms,正常延迟时差占比为100%,标准差为0,则评价结果Y=1;RSN=4时,平均延迟时差为1.95ms,正常延迟时差占比100%,标准差为0.19,评价结果为Y=0.91;类似地,RSN=3时,Y=0.85;RSN=2时,Y=0.65。加入面波后,正常延迟时差均值为2.0ms,正常延迟时差占比为61%,正常延迟时差的标准差为0.12,评价结果为Y=0.55。

综上分析,无噪声时,延迟时差数值稳定。含噪声时,延迟时差对信噪比变化敏感,随着信噪比降低,延迟时差逐步发散,此时成像振幅与理论反射系数相对误差逐渐增大,成像保真度降低,这与评价结果逐渐降低的趋势保持一致,进而说明该评价函数可有效区分成像前数据的质量。加入面波后,面波存在区域的反射波时差关系受到破坏,使得延迟时差锐减,导致评价结果显著降低。为得到较准确的评价结果,在扫描延迟时差时须避开强能量面波区域。

当层间间距为延拓步长的10%～30%时,可得到与外推步长保持一致时接近的振幅计算结果[18]。换言之,在成像时延拓步长采用层间间距的3～10倍,也可获得较好的振幅计算效果。因而,在实际资料采集过程中,设置层间间距时应充分考虑检波器灵敏度或者允差,在保证层间时差能被分辨的前提下,适当缩小间距,以控制成本。例如当检波器灵敏度为0.2ms时,假设地表速度为1000m/s,则层间间距可设置为0.2m。同时,应采用组合检波等手段压制干扰,尽可能提高原始资料的信噪比。数据处理过程中,在做到相对保幅处理的同时,应采用多域组合去噪方法,充分压制规则干扰,衰减背景噪声,以保证双检数据的信噪比高于3。

3.2 实际资料测试

作业区位于山东孤北地区,该区域地形平坦,以水平地层为主,地质构造相对简单。本次二维双检地震数据采集采用多次覆盖观测系统,固定排列,炮点滚进滚出,具体采集参数见表1。该原始数据某时窗上下层波形关系如图7所示。将原始炮集按炮号分段后,分别扫描层间延迟时差、道间延迟时差、层间振幅差、道间振幅差、层间正常延迟时差占比和道间正常延迟时差占比6个指标,得到如表2所示的扫描结果。

表1 孤北二维双检数据采集参数

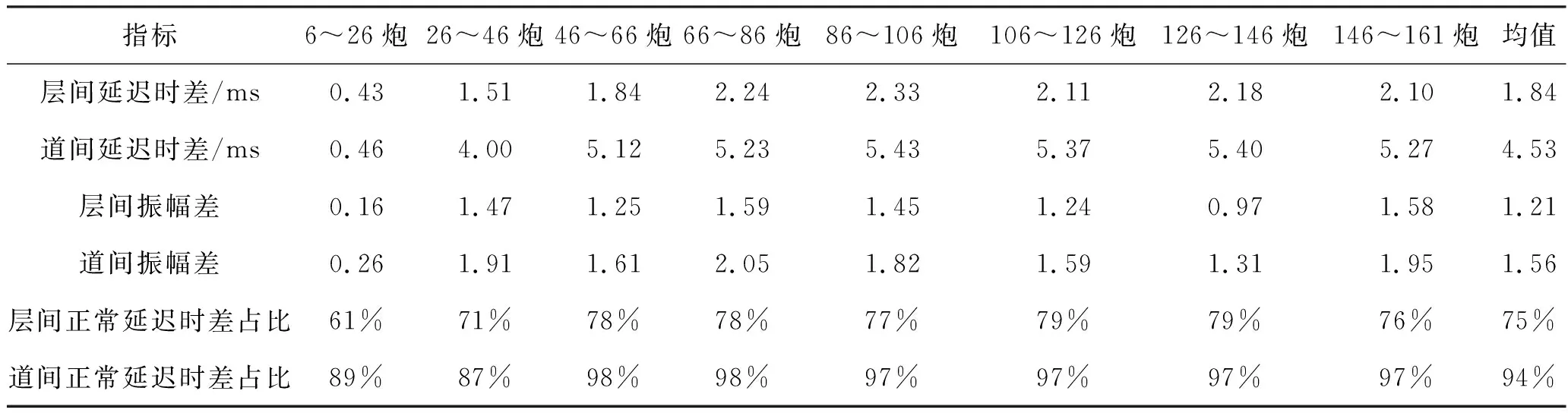
表2 孤北二维双检数据各项指标扫描结果

图7 双检实际资料原始数据波形关系

各项指标按公式(13)去量纲化后的变化规律与各分段数据的评价结果如图8所示。

图8 实际数据各指标扫描结果及评价结果

(13)

式中:zm为指标数值;M为参数的数量。

分析图8可知,层间延迟时差和道间延迟时差、层间振幅差与道间振幅差趋势吻合程度高,评价值与各评价指标变化趋势基本一致。说明以层间延迟时差作为主要指标,其它指标作为参考指标的评价函数具有较好的稳定性和抗噪能力。

由表2数据计算本次实际资料的总体评价结果。加权相关系数为0.95,层间延迟时差占比均值为0.75,层间延迟时差均值为1.84ms,层间延迟时差标准差为0.63,最终评价结果Y=0.53。分析扫描结果曲线可知,6～36炮层间和道间延迟时差及振幅差均低于主分布轨迹,导致评价结果偏低。剔除6～36炮后,计算得Y=0.86,评价结果明显变好。针对不同的评价结果,选取相等炮数,经相同流程处理后进行双检成像对比。图9a为6～36炮与60～90炮双检成像剖面对比,图9b,图9c和图9d分别为图9a中蓝色箭头所标示位置成像剖面细节对比,图9e为提取细节图中红色虚线所示层位的成像振幅对比。

以全炮集数据成像结果作为参考标准,相较于评价结果较差的6～36炮,评价结果较好的60～90炮构造成像更完整,标示位置成像细节剖面虚假成像和成像噪声更少,成像振幅无明显偏差,保幅性好。因此,评价结果较差的部分其构造成像和成像保幅性都差。

评价原始数据时,对评价结果低于0.6的部分,应细化评价尺度,分析原因。由延迟时差紊乱等原因所导致,应该进一步校正时差;由噪声原因引起,建议去噪处理后重新评价。对于处理环节中的数据,当评价结果小于0.6时,在原始数据合格的前提下,应检查前置处理环节是否破坏了层间延迟时差关系。

4 结论

本文针对陆地双检采集系统实际资料成像效果不理想的问题,从双检波器成像原理出发,通过分析层间延迟时差对双检成像的影响,建立了基于延迟时差的陆地双检地震数据评价方法。该方法可用于定量评估原始资料的合格性,也可作为双检数据处理质量监控的一种手段。同时,该方法为双检数据采集时检波器间距设置和信噪比要求提供了参考,进一步推进了陆地双检勘探技术的工业化进程。另外,本文提出和验证了层间延迟时差对于双检构造成像和保幅性的重要意义,并给出了基于互相关的层间延迟时差定量计算方法。

本文提出的评价方法易于实现,适用于评价各阶段双检数据,区分度高。但在实际操作过程中,选取不恰当的分析时窗、或设定不合适的正常延迟时差阈值,都会对评价结果产生一定的影响。对于评价结果较差的部分,还需进一步细化评价尺度,分析原因,以消除人为因素及噪声等造成的误差。此外,发展适合于双检数据的高信噪比采集技术、保幅处理技术、双检数据延迟时差校正技术等,对于双检波器采集系统的工业化应用具有重要意义。利用海上双检数据实现保幅偏移,具有良好的应用前景,还有待进一步研究。