电机定子绝缘频域介电谱解析与老化评估方法研究

石 颉 赵德宇

(苏州科技大学电子与信息工程学院 苏州 215009)

1 引言

定子绝缘作为发电机的主绝缘结构，其绝缘故障是电机的主要故障之一，温度、电场、机械振动都是导致其绝缘状态不断下降的因素[1]，为避免定子绝缘故障，有必要定期对其进行老化状态评估。基于频域介电响应的频域介电谱法(Frequency- domain dielectric spectroscopy，FDS)因其试验电压低、携带绝缘信息丰富、对绝缘老化敏感度高、测量结果分散性小等特点，在定子绝缘老化状态评估中对比所需试验电压高、破坏性强、结果分散性大的绝缘电阻试验与耐压试验等传统方法具备明显的优势。近年来，频域介电谱法已在电气绝缘领域得到了充分的应用[2-3]，但相应的频谱分析策略和通过特征量进行老化状态评估的方法仍处于不断探索阶段。

利用Debye介电弛豫模型及其优化模型对介电谱进行拟合分析是实现频谱特征量提取的有效手 段[4-7]，但此类介电弛豫模型并未对介电响应的电导损耗加以考虑。为解决这一问题，国内外学者对其展开了大量研究，主要分为两条技术路线：其一是通过提高测试频率以减小电导的影响[8]，高频率测试结果虽然减少了电导损耗的影响，但却不能反映绝缘材料实际工作状态；其二是引入电导参量对介电弛豫模型进行完善，从国外学者TUNCER等[9]引入复电导对介电弛豫模型进行修正开始，国内以重庆大学杨丽君教授为代表的学者在此基础上进行了大量研究[10-11]，但该方法仍存在以下弊端，如低频段电导损耗量有可能将弛豫极化量掩盖使得难以准确判断弛豫数量[12]、电导损耗量与弛豫极化量统一建模可能导致参数之间的互相影响，产生多个Pareto解等。

根据FDS测试结果与相应的介电弛豫模型 参数对材料进行老化评估是业内常用的诊断方 法[13-14]。而使用模型参数进行老化状态评估对参数的精确度有较高的要求，更适用于单弛豫或不同弛豫之间交联较少的情况。当测试频段谱图未显示弛豫峰或弛豫数量较多时无准确约束模型参数的范围，导致参数求解不精，且过多的参数使彼此之间的联系加深，易产生多个Pareto解，无法利用单一的参数实现老化评估。

为解决上述问题，实现高低频段介电响应曲线的统筹分析及利用介电弛豫模型特征参量对定子绝缘老化状态进行评估，本文在众多专家学者的研究基础上提出了对频域介电谱进行解析的具体方法，设计了定子线棒的加速老化试验，验证了所提方法的有效性，并对相应的老化评估方法进行了深入探讨。

2 频域介电谱解析策略

2.1 FDS理论基础

FDS测试通过对绝缘材料施加交变电场，采集介电响应电流并获取复相对介电常数以诊断材料的绝缘状态。

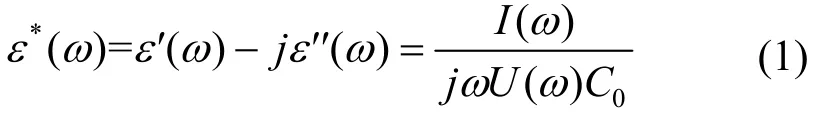
式中，U(ω)为角频率为ω的交变电压；I(ω)为响应电流，包含容性电流与阻性电流，同时包含着极化电流与电导电流，二者的区分是电介质介电响应测试的关键技术之一[15]；C0为真空几何电容，仅与该电介质形状有关；ε(ω)是复相对介电常数，ε′(ω)与ε′′(ω)分别对应复相对介电常数的实部与虚部，包含介电响应的极化与电导信息，其中实部表征极化与电导反应中电荷的储存，而虚部则表征能量的损耗。FDS测试结果通常以ε′(ω)与ε′′(ω)在频率区间的谱图展示。

介电弛豫模型对复相对介电常数中包含的单个弛豫极化量εp*(ω)进行了解释，其中HN(Havriliak-Negami，HN)模型[16]是适应度最高的模型

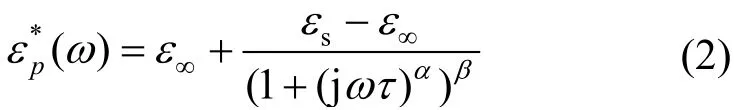
式中，εs为该极化弛豫的静态介电常数；ε∞为无穷频率介电常数，即光频介电常数；εs−ε∞称为弛豫极化强度幅值；τ为弛豫时间；α与β为其弛豫形状参数(0<α，β≤1)。

电介质的介电响应中，除了弛豫极化反应之外，其内部还因载流子的输运存在电导反应[17],电导反应仅对复相对介电常数虚部产生贡献，即电导过程仅存在能量的损耗，不产生电荷的储存。

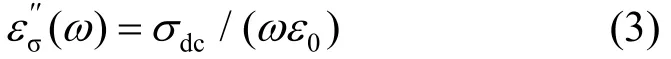
式中，σdc为直流电导率；ε0为真空介电常数(ε0=8.854 pF/m)；εσ′′(ω)为由电导反应产生的能量损耗。当弛豫数量越多，弛豫数量的判断越困难，建立的模型越为复杂。为实现准确判断弛豫数量以及在建模分析过程中避免Pareto解的产生，须对上述模型进一步分析。

2.2 弛豫数量的判断

相关研究多通过观察复相对介电常数的复平面图的圆弧数或虚部图的峰数来判断频段内的弛豫数量[18]。

如图1所示，单一弛豫的复相对介电常数的虚部图为峰型，复平面图为近圆弧状，弛豫峰对应的频率为特征频率ω0，该介电弛豫过程的弛豫时间τ= 1/ω0。实际测试中，所测频段的复相对介电常数可能包含着电导量及多个极化弛豫量。电导量与弛豫量以及不同弛豫量之间可能存在交叉、重叠、覆盖现象，从而影响复平面图与复介电常数虚部图的形状，导致极化过程数量的判断不准确。

图1 复相对介电常数虚部图与复平面图

除了介电弛豫模型之外，复相对介电常数实部与虚部之间还遵循着Kramers-Kronig方程关系[19]

联立式(2)与式(4)，对单个弛豫过程ε′(ω)与ε′′(ω)的关系进一步推导可得

(εs−ε∞)/2ln10是未知常数，并不影响曲线形状，即曲线与εp′′(ω)曲线形状一致，通过该曲线形状可判断弛豫数量。

2.3 电导损耗的分离

式(3)显示电导损耗随频率的升高而下降，在频率与损耗的双对数坐标系下呈-1的斜率，假设极限条件下，测试频段内最低频率点电导损耗占据复相对介电常数虚部的100%，当测试频率上升3个数量级之后，电导损耗占比迅速下降为1‰，理论上可以忽略不计。据此，将测试频段覆盖多个数量级，利用高频段复相对介电常数进行介电弛豫模型的拟合分析，可忽略电导损耗的影响。将拟合结果推广到测试全频段，可实现电导损耗与弛豫极化损耗的分离，以获取低频段的介电响应特征，同时避免直流电导率这一关键参数产生多个Pareto解。为提高可靠性水平，测试频带应足够宽，以前3个数量级频段作为低频段，其余作为高频段。为避免高频段可能存在的多弛豫交叉、重叠等现象，介电弛豫模型的弛豫数量必须通过全频段的曲线进行判断，否则无法将拟合结果向低频段推广。

为保障所得模型参数的可靠性，在将高频数据的模型拟合结果向低频数据进行推广时，必须对拟合推广结果与原始数据的一致性进行检验，检验通过后才能输出模型参数。复相对介电常数虚部全频段推广结果不包含电导损耗，与原始数据具有明显的差异，故检验可对复相对介电常数实部进行。检验可通过相关系数与决定系数进行，综合上述分析，对频谱进行分析策略流程图如图2所示。

图2 频谱分析流程图

2.4 老化评估方法探究

通过上图算法分离出的电导损耗与弛豫极化损耗相互独立，不受弛豫极化损耗的影响，因此可通过不同绝缘状态材料FDS信息中电导损耗的变化规律实现待测样品的老化评估。然而相较于电导而言，材料的极化更能反映其内部的微观运动特性，蕴含的内容也更为丰富[20]。由于FDS测试获取的介电弛豫量源于频域介电响应极化电流，而时域介电谱测试—极化去极化电流测试通常使用时域电流分析材料的老化状态[21]，且频域信号与时域信号之间可以互相转换。鉴于此，可将频域电流通过傅里叶逆变换转换为周期性的时域电流以实现单个弛豫量总体强度的分析，避免单个或多个参数对老化不敏感、可靠性较低等问题，统一时域电流周期可实现不同弛豫量的定性分析。

根据电介质介电响应机理[22]，当对厚度为d的电介质施加变电压U(t)时，产生空间均匀电场E(t)=U(t)/d，则电介质的内部介电响应有

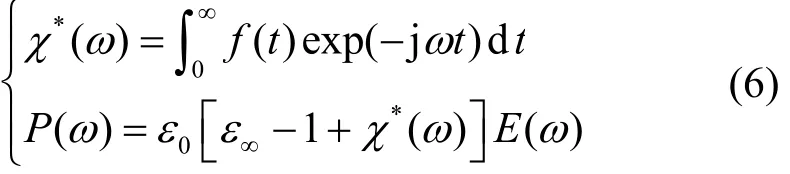
根据上述公式，得到电介质内部单个极化过程的极化电流密度在时域与频域的表达式为

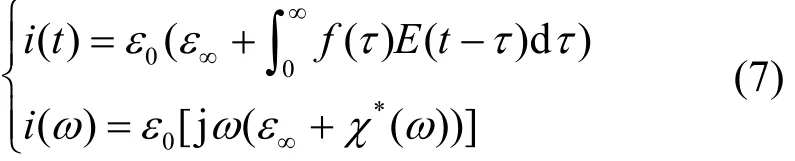
对频域介电响应的极化电流i(ω)进行傅里叶逆变换获得时域极化电流i(t)为

3 应用实例

电机定子绝缘的主要组成材料为环氧云母复合绝缘，大量研究已证实环氧云母绝缘具有良好的介电响应特性[11,16]。设计加速老化试验获取对不同绝缘老化状态的定子绝缘进行FDS试验，并通过上述方案对获得的介电响应曲线进行分析。

本文所用样品为上海某电力公司提供的定子线棒，主绝缘为F级环氧云母复合绝缘，绝缘厚度3.5 mm。所用恒温箱为温度精度±1 ℃的RL100型老化烘箱，FDS测试选择Megger公司生产的IDAX-300介谱分析仪，测试频率范围为10−3～ 104Hz，每个数量级频率区间等对数间距选择10个频率点。试验采用电-热加速老化，将定子线棒试样放入恒温箱并进行加压加温试验。老化电压设置为30 kV，温度为180 ℃。每192 h进行一次FDS测试，重复测试两次取平均值，测试在室温下进行。

试验采用三电极结构[23]，试验前需要将样品预处理：两端剥离20 mm绝缘材料露出铜棒作为高压电极；中间320 mm涂抹低电阻漆并紧密贴上铝箔作为测量电极；高压电极两侧各涂抹50 mm的SiC防晕漆防止电晕放电；防晕漆与低电阻漆之间的 20 mm间隔作为保护电极接地，避免泄漏电流对测试结果产生影响。试验原理图与测试结果见图3与图4。

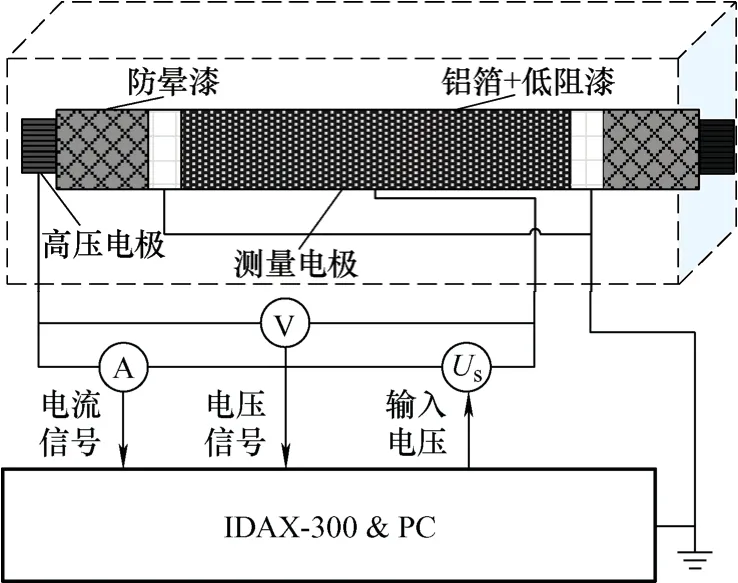
图3 试验原理图

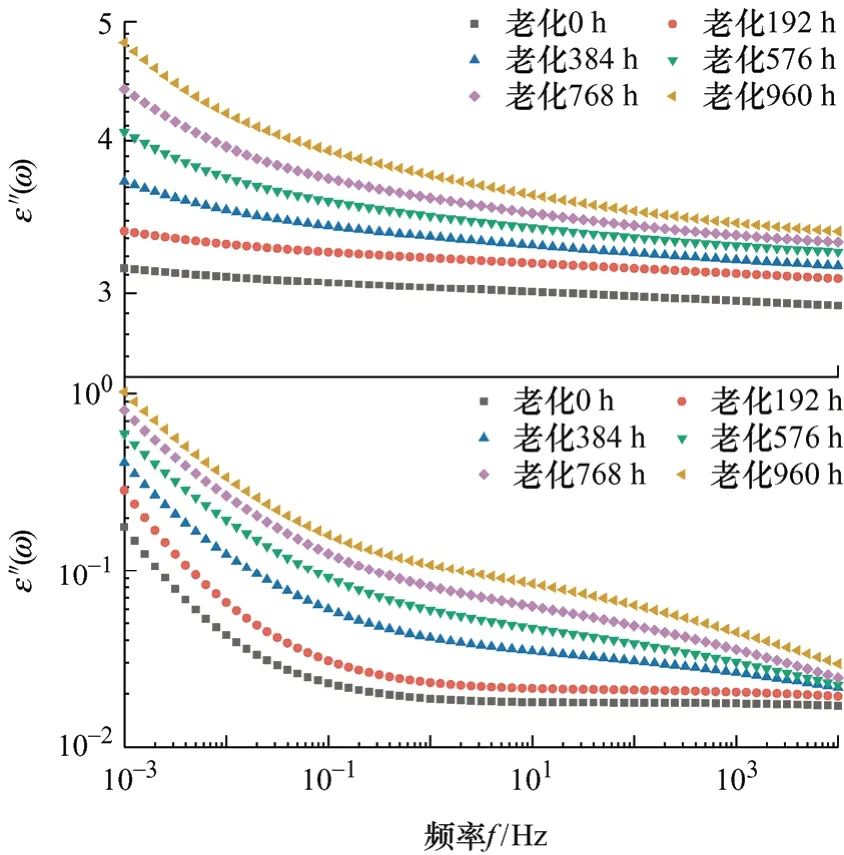
图4 FDS测试结果

由于复相对介电常数虚部包含电导损耗，不可直接根据其形状进行弛豫数量的判断。根据上节理论进行弛豫数量判断，用差分法得到曲线，如图5所示。

图5 差分法提取后的曲线

所得曲线在频率区间内出现了一次下降速率的改变，不符合单一弛豫过程的形状特性，可判断所测频段内至少存在两个弛豫过程。对高频段数据进行双弛豫HN模型的建模分析

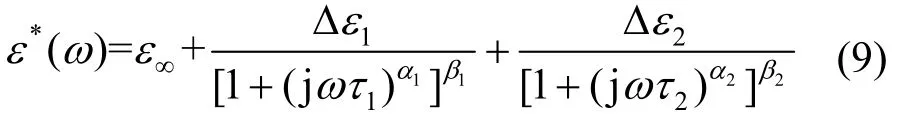
式中，Δε1、Δε2与τ1、τ2分别为两个弛豫过程的弛豫极化强度幅值与各自的弛豫时间；α1、β1与α2、β2分别为两个弛豫过程的形状参数。利用最小二乘法原理对实测数据进行建模分析可实现模型参数的最优化求解，具体步骤如下：① 提取ε*(ω)的实部与虚部，建立方程组；② 将实部、虚部拟合值与测量值的误差平方和作为目标函数；③ 设定初始HN模型参数值，通过反复迭代求解更新模型参数使拟合值与测量值的误差平方和最小。误差平方和(Sum of squared error，SSE)的计算公式为

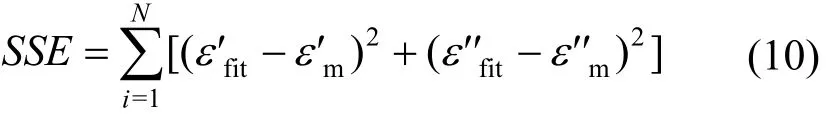
式中，ε′和ε′′分别为复相对介电常数的实部和虚部；ε′fit与ε′m、ε′′fit与ε′′m分别为ε′和ε′′的拟合值与测量值；N为测试样本数量。

将高频段内的求解结果推广到全频段，经检验后输出结果，获得仅含有极化信息的复相对介电常数的实部与虚部，将拟合虚部值与实测虚部相减之后得到电导损耗，HN模型拟合结果与电导损耗分离结果如图6所示。

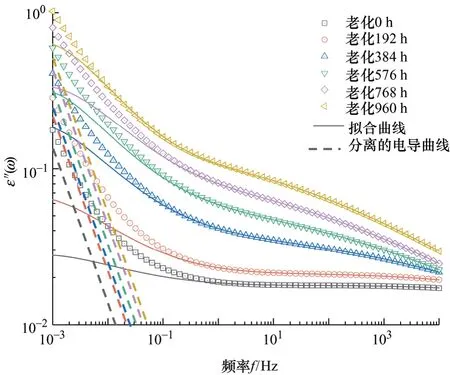
图6 HN模型拟合及电导分离结果

对分离后的电导损耗使用式(3)进行拟合，可获取不同老化周期的直流电导率。由于试验数据误差与两个弛豫过程都并未显现弛豫峰这一特点，存在多组参数使误差平方和最小值极为接近且难以取舍，导致两个弛豫过程的弛豫时间参数与形状参数出现多组Pareto解。以老化192 h为例，其中5组Pareto解如表1所示。

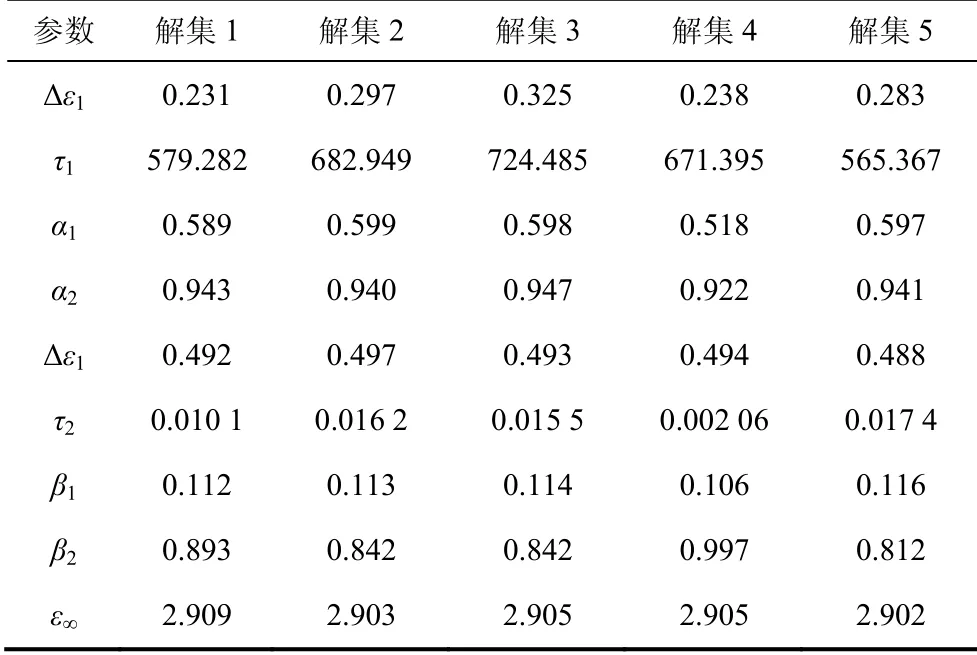
表1 老化192 h双弛豫HN模型参数求解结果

对表中5个解集分别进行傅里叶逆变换，并统一电流周期(本文取7 000 s，可自由设置)，获取弛豫过程1的时域等效电流如图7所示。

图7 老化192 h弛豫过程1的时域等效电流

由图7可以看出各Pareto解对应的介电弛豫模型参数不同，但经过转换后的等效电流基本重合，验证了所提方法可以实现单一极化类型弛豫量整体分析的可行性。由于统一了时域电流周期，仅对比电流幅值即可分析弛豫量的变化规律。每个老化周期任意取一组Pareto解，具体解集参数如表2所示，获得所示转换后的时域极化电流幅值，如图8所示。

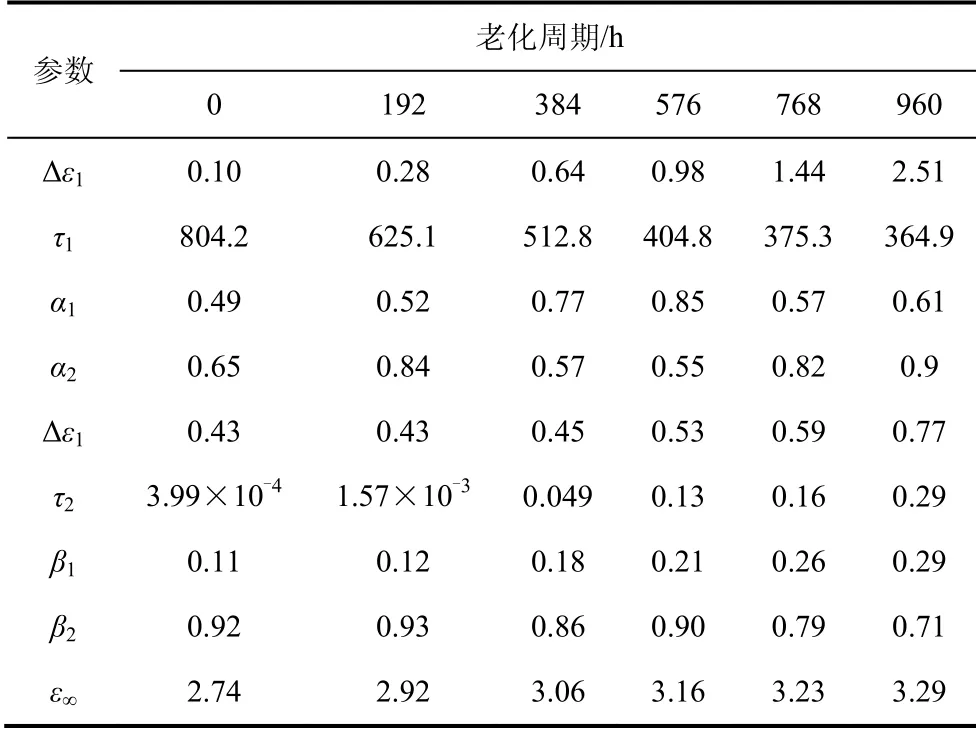
表2 不同老化周期所用介电弛豫模型参数

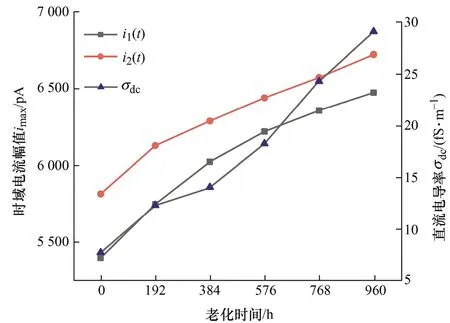
图8 时域电流幅值与直流电导率随老化周期的变化

结果显示不同极化类型的电流幅值与直流电导率均随老化程度的增加呈上升趋势，展现出良好的规律性，实际测试中可通过此数值规律对被测定子绝缘的老化状态进行评估。

4 结论

本文提出了频域介电谱的具体解析方法与老化评估手段，设计电机定子绝缘的加速老化试验进行了验证，所得如下主要结论。

(1) 利用实测复相对介电常数实部与角频率的偏导曲线可实现测试频段内极化弛豫数量的判断。

(2) 对高频段复相对介电常数进行介电弛豫模型的拟合，并将拟合结果推广到全频段，可实现电导量与弛豫量的剥离。

(3) 将频域极化电流通过傅里叶逆变换，可以将频域极化电流转换为时域极化电流，通过时域电流幅值和直流电导率随绝缘老化的变化规律可以实现电机定子绝缘的老化状态评估。