LCL型电力弹簧的设计及控制策略研究*
2021-07-31袁昌海丘东元
袁昌海 丘东元 张 波
(华南理工大学电力学院 广州 510000)
1 引言
随着我国在2020年向全世界作出了“碳达峰、碳中和”的承诺,“十四五”期间势必将有更多的新能源并网,到2030年我国风电、太阳能发电总装机容量将达到12亿千瓦以上,新能源渗透率不断提高。由于风能、太阳能发电具有间歇性、波动性等固有特性,当这些分布式可再生能源大范围、高比例地接入电网后,就可能出现用电量与发电量的严重不匹配,甚至可能出现从用户到变电站的功率倒流[1-2],从而导致电网过电压[3]、电压波动[4],进一步可能造成继电保护装置误动作,损坏并网设备,甚至导致停电事故[1,3-5]。为了解决可再生能源并网所造成的电压波动或功率不平衡问题,目前主要采用以下几种方法:① 有载调压变压器分接头或步进电压调节器;② 无功补偿装置;③ 分布式储能系统;④ 需求侧管理。但是以上方法存在一定的局限性:① 变压器有载调压或者步进电压调节器采用机械结构无法快速且准确地解决电压波动问题,因此必须和其他措施相结合[6];② 无功补偿如FACT装置无法彻底解决有功不平衡的问题[7];③ 分布式储能可以最大化利用可再生能源,但其储能系统成本较高并可能会对环境造成污染[8-9];④ 目前需求侧管理采取的负荷控制措施通常会对用户用电造成很大的影响,例如分时电价措施在某些条件下不能起实质作用而且有很大的滞后性[10-11]。
为了更好地解决可再生能源并网造成的电压波动问题,香港大学Shu Yuen (Ron) Hui团队于2012年首次提出了电力弹簧(Electric spring, ES)的概念,其核心思想是将来自公共耦合点(Point of common coupling, PCC)上游的电压或功率波动转移到非关键负载(Non-critical load, NCL)上,从而实现PCC或关键负载(Critical load, CL)的电压稳定[12]。ES实际上属于一种新型的需求响应措施,实现了用电量随发电量的变化而变化的电网运行方式。经过近十年的发展,目前ES主要可以分为三代:ES-1、ES-2和ES-3。ES-1伴随着ES的概念被提出来,由半桥或全桥电压型逆变器实现[12]。ES-1直流侧只有电容,因此只能进行无功补偿,有功补偿则通过控制NCL功率的增加或减少来间接实现。ES-2在ES-1的基础上将直流侧电容替换为直流电压源,因此能够实现直接的有功补偿,扩大了ES的工作范围[13]。进一步地,ES-3去掉了NCL,直接进行有功和无功补偿[14],但是从拓扑的角度来看ES-3和储能装置或UPS类似,而且由于没有NCL参与,ES-3所需要的储能成本相比ES-2会更高。因此,与ES-2和ES-3相比,采用纯无功补偿模式的ES-1仍是一种比较经济可靠的方案。其他衍生ES还包括采用变压器隔离的隔离式ES[15]、采用电流源逆变器的CSI-ES[16]、采用背靠背变换器的B2B-ES[17]等。但是大部分ES均是基于ES-1所做的改进,在拓扑上具有一个共性,即ES和NCL串联连接。在这种结构下,当ES运行于纯无功补偿模式下,ES无法大范围调节NCL的端电压,其功率补偿范围十分有限。
为此,本文提出了一种基于无源阻尼LCL滤波器的电力弹簧(LCL-ES),将NCL作为LCL滤波器的无源阻尼并联在滤波电容两端,这种结构能够有效提高NCL端电压的调节范围,从而扩大了ES的功率调节范围。本文的内容安排如下:首先介绍了LCL-ES的拓扑结构和工作原理,然后分析了其稳态运行时的功率范围,接着讨论了LCL-ES稳态运行时可允许的网侧电压波动范围,即稳压能力。基于上述分析,本文初步给出了LCL-ES主电路参数和控制策略的设计方法,最后通过仿真和试验结果验证了LCL-ES拓扑的有效性及其稳态运行范围分析的正确性。
2 工作原理
电力系统中的负载可以分为两大类:一类为CL,其端电压只允许在极小范围内波动,它的稳定也是ES的控制目标;另一类为NCL,其端电压可以在较大范围内波动。ES通过改变NCL的功率大小,在“颠簸”的电网中将来自可再生能源的有功功率波动转移到NCL上。传统的串联型ES如图1所示,逆变器的交流侧接LC滤波器,滤波器的输出与NCL串联,组成功率可控的串联型智能负载(Smart load, SL)。由于ES和NCL的电压之和等于PCC电压,因此通过控制ES输出电压相量Ves的幅值和相位可实现稳定PCC电压的目标。
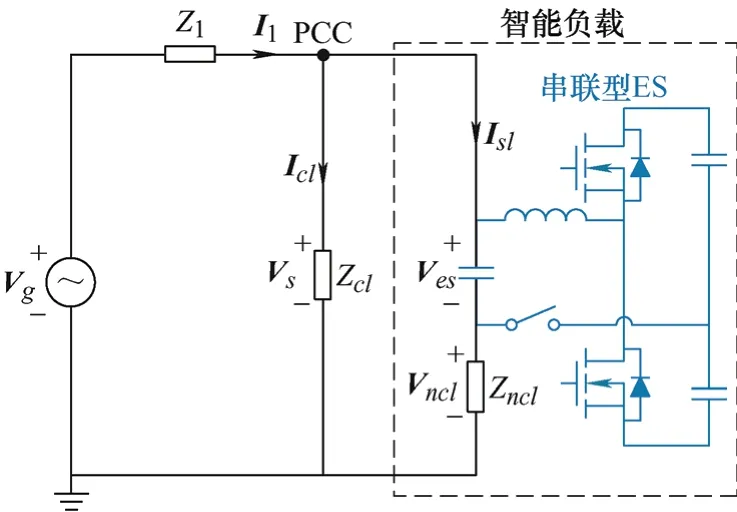
图1 传统串联型ES
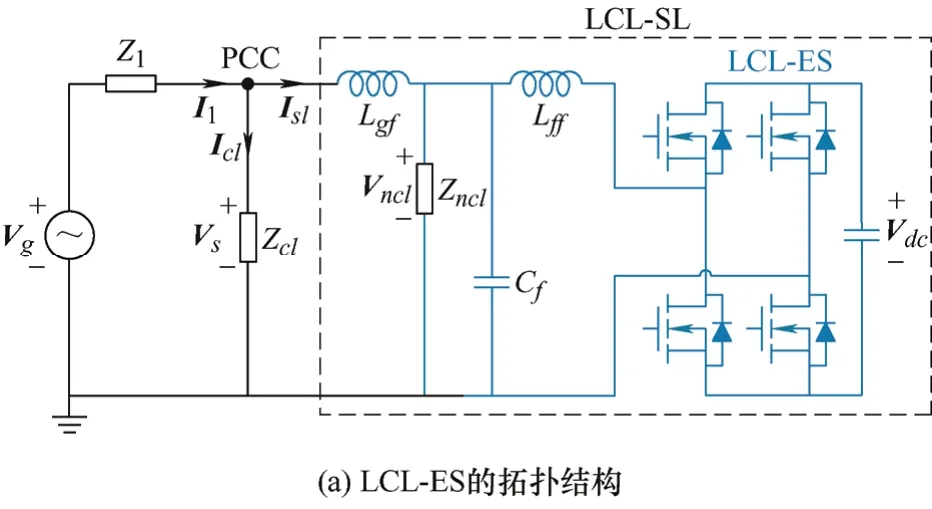
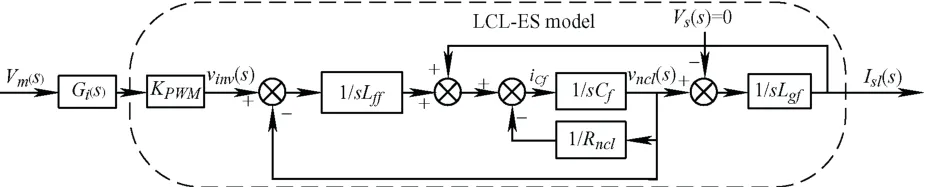
本文所提的LCL-ES拓扑结构如图2a所示,逆变器的交流侧接LCL滤波器,其中NCL作为无源阻尼与滤波电容Cf并联,共同组成LCL型智能负载(LCL-SL)。设流入LCL-SL的电流相量为Isl,NCL的端电压相量为Vncl,PCC或CL的电压相量为Vs。LCL-SL的交流相量关系如图2b所示,故有Vncl=Vs−jωoLgfIsl,其中ωo(=2πfo)为电网基波角频率。当Isl相位超前于Vs时,Vncl幅值大于Vs;当Isl相位滞后于Vncl时,Vncl幅值小于Vs。通过改变Isl的相位和幅值即可改变Vncl的幅值,从而在Vs幅值恒定的条件下,调节NCL功率实现需求响应。
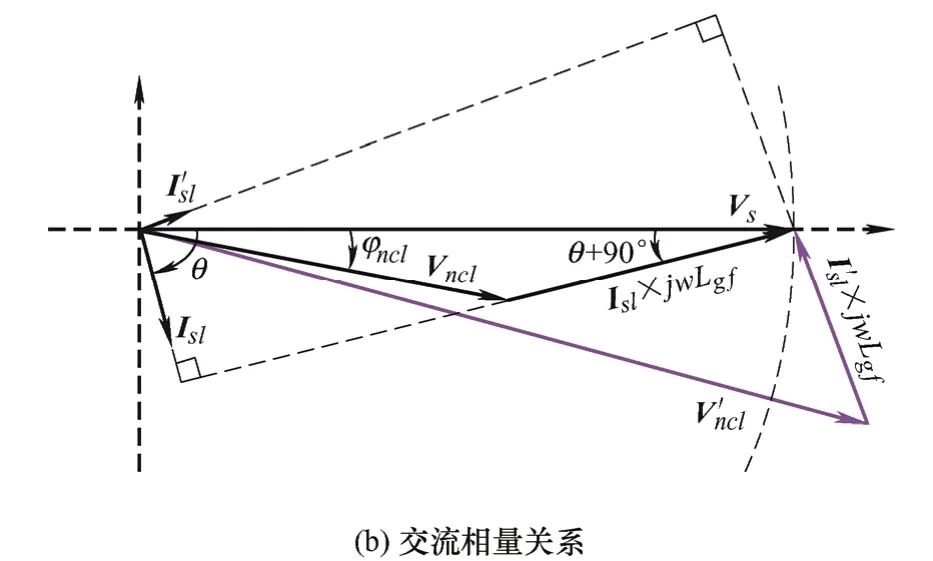
图2 LCL-ES拓扑和交流相量关系
3 功率补偿特性
当逆变器的直流侧接纯电容时,ES将运行在纯无功补偿模式,对外不进行有功功率的交换,即Pes=0,该运行方式最为经济实惠,因此本文仅讨论ES提供纯无功补偿的情况。
当串联型ES稳态运行时,如图1所示,串联型SL吸收的有功功率Psl、无功功率Qsl以及NCL的有功功率Pncl为
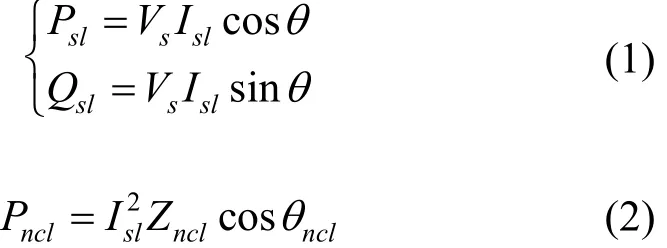
式中,Vs和Isl分别为相量Vs和Isl的有效值,θ为Isl滞后Vs的角度,NCL用阻抗Zncl表示,其阻抗角为θncl。结合式(1)和式(2)可以得到Pncl、Psl和Qsl之间的关系为
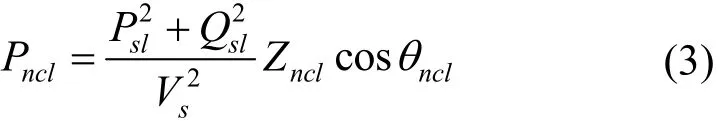
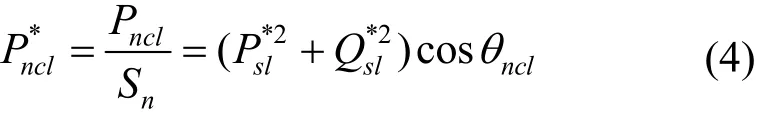
纯无功补偿模式下Psl=Pncl,则上式可以改写为
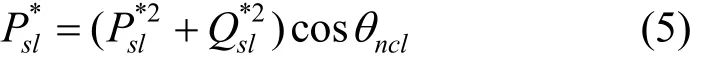
对于LCL-ES,根据图2b所示相量关系,利用余弦定理可以得到Vncl的幅值Vncl为
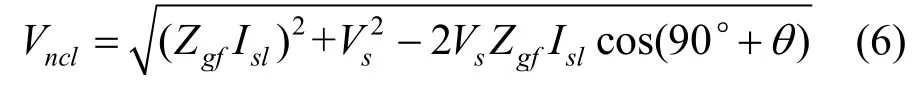
式中,Zgf=ωoLgf,θ为Isl滞后Vs的角度。
LCL-SL吸收的有功功率Psl和无功功率Qsl表达式同式(1)。NCL消耗的有功功率Pncl为
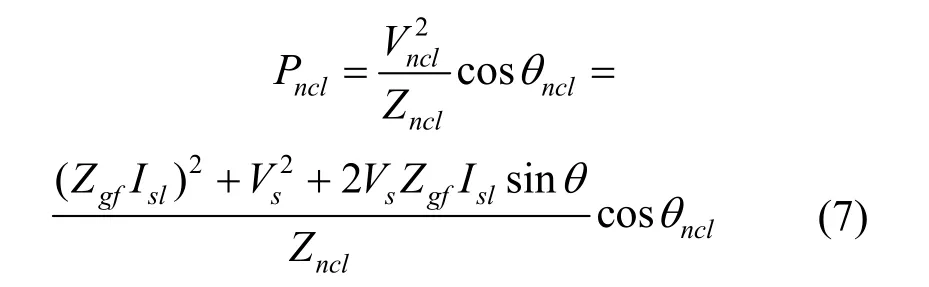
以功率Sn为基准值,上式可归一化为

其中a=Zgf/Rncl。当LCL-ES运行在纯无功补偿模式时,式(8)可改写成
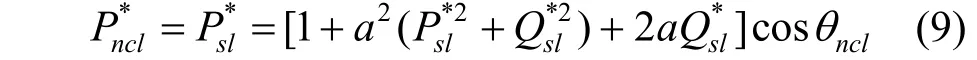
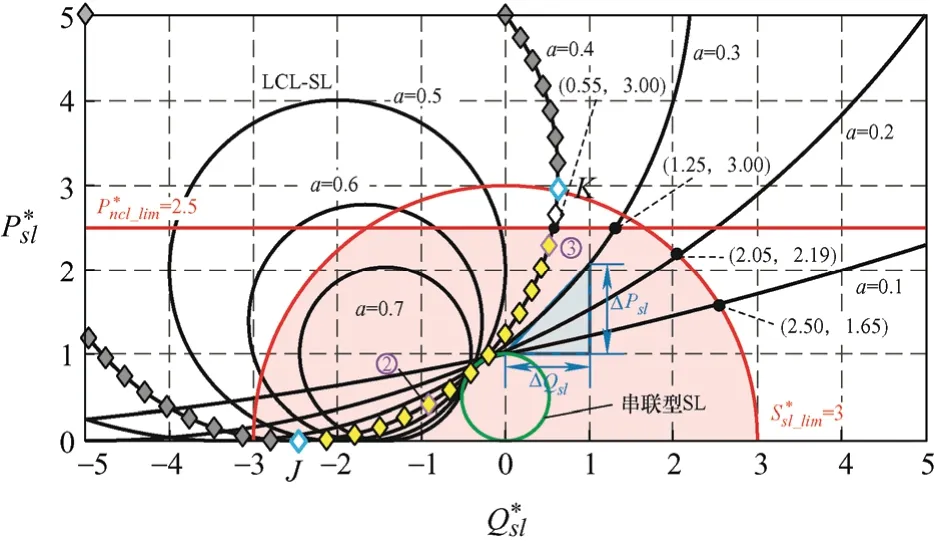
图3 LCL-ES和传统串联型ES的功率曲线
4 网侧电压波动的抑制能力
第3节分析的是LCL-ES稳态运行时的功率范围,本节分析的是稳态运行时所允许的网侧电压波动范围[18],其基本思路是将图2a所示电力系统视为单输入Vncl单输出Vg系统,首先根据图2b所示的相量关系计算出纯无功补偿模式下NCL的端电压Vncl范围,根据输入和输出之间的关系即可推算出网侧电压Vg的范围。
设Vg为网侧电压相量,Z1为传输线等效阻抗,I1为网侧电流相量,CL的阻抗为Zcl。根据图2a所示电力系统可以得到
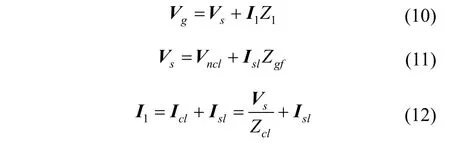
将式(12)和(13)代入式(11)可以整理得到
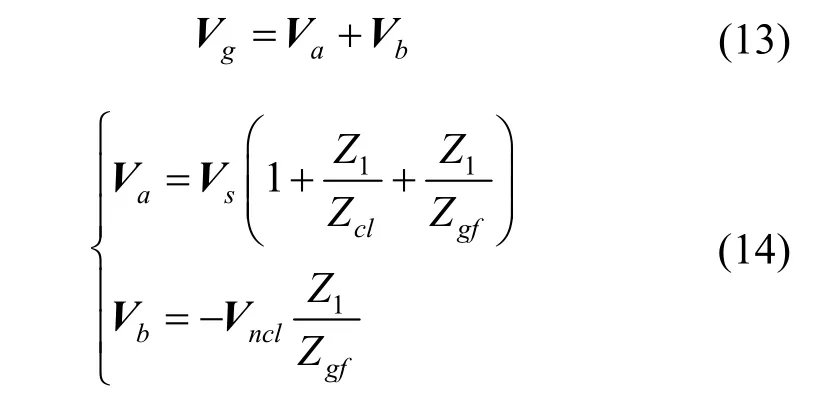
其中各阻抗的参数表达式如下
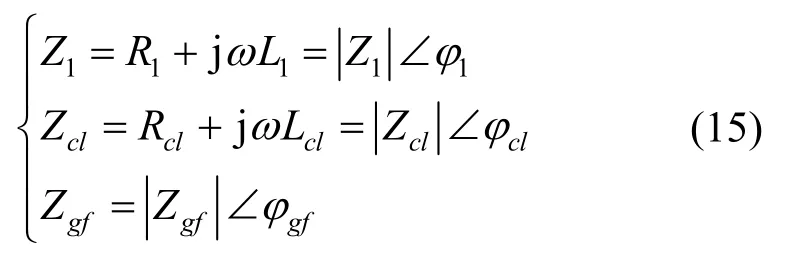
并网电感阻抗Zgf忽略等效电阻则ϕgf≈π/2。以Vs为参考相量,则Va为常相量,其大小和方向仅仅与网络阻抗参数有关。为了求出Vb,可以首先求出Vncl。为了便于分析计算假设Zncl=Rncl,则LCL-ES纯无功补偿模式下根据Psl=Pncl有
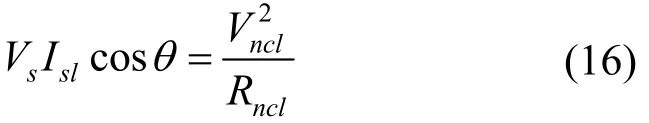
将式(16)代入式(6)可以得到如下方程
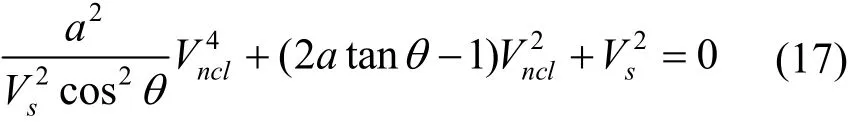
根据韦达定理可以得到Vncl的两个实数解为

考虑到LCL-SL有功功率大于零及式(18)的解应为实数,可以得到
可确定θ范围为
结合图2b,利用余弦定理可以求得Vncl的相角为
根据式(18)和式(21),已知θ则可确定Vncl。当a=0.4时,在θ范围内取一系列点即可得到各个相量的轨迹如图4所示。当LCL-ES运行于纯无功补偿模式时,图2b中的各个相量的所有可能组合所构成的轨迹为三个相交的圆。假设Vncl的轨迹圆心为O1,半径为R1,如图4a所示,当Vncl和Vs正交时Vncl达到最大值2R1,此时有如下关系

图4 相量轨迹
可以得到R1=Vs/(2a)。已知Vncl轨迹,再根据式(13)和式(14)表示的从Vncl到Vg的映射关系可以得到
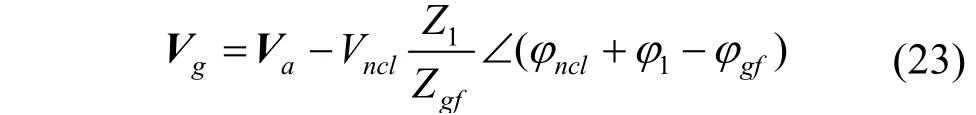
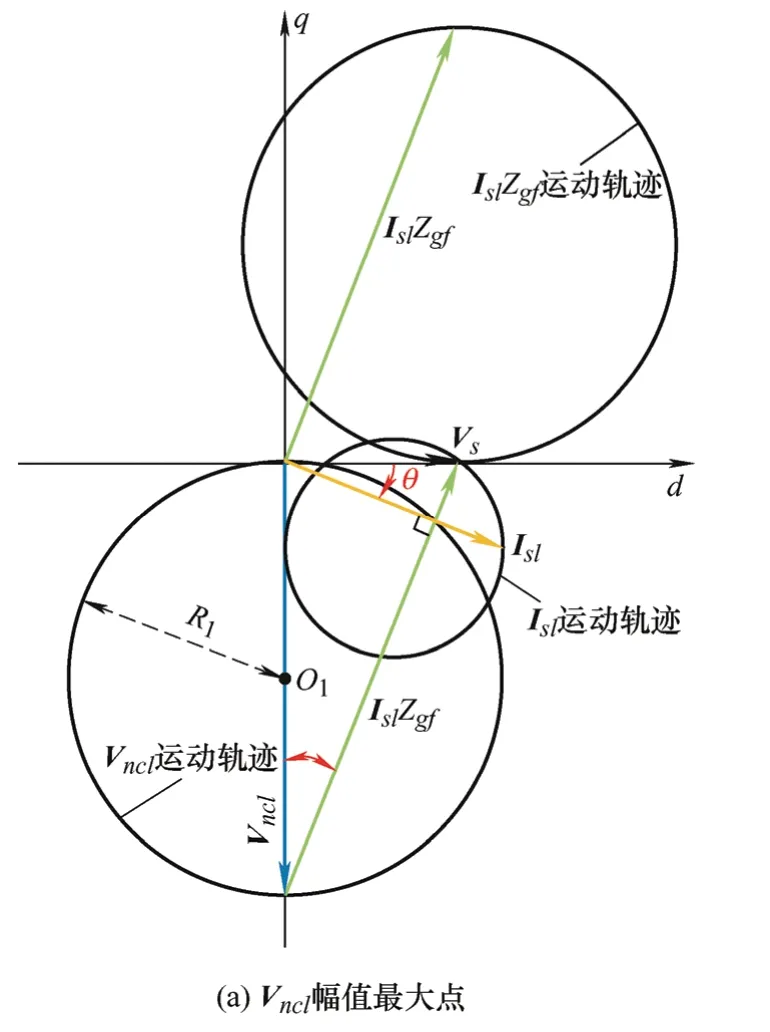
对于纯电阻NCLnclϕ≈0,于是可以得到Vg的运动轨迹如图5所示。Vg的轨迹也为圆形,圆心为O',半径为R。结合式(23)和Vncl轨迹半径R1可以得如下结果
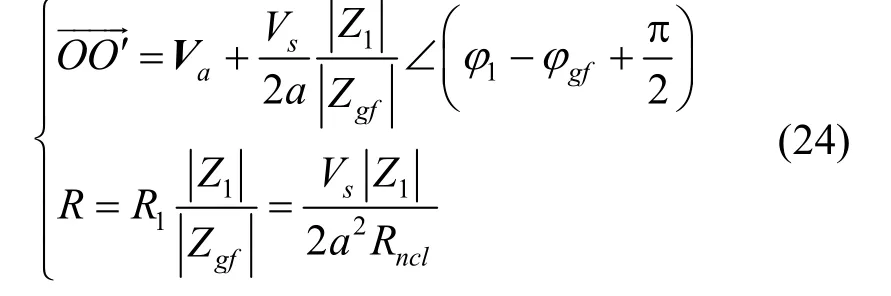
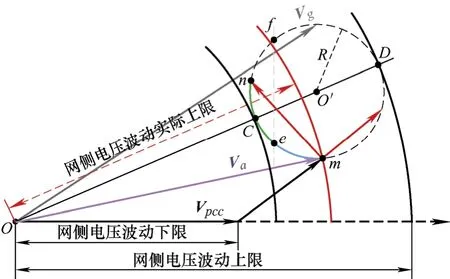
图5 Vg的轨迹
根据图5,LCL-ES的稳压调节能力也是有一定限制的,当且仅当网侧电压幅值在轨迹范围内时系统才可以达到稳定。
以网侧电压幅值Vg为半径的圆可能与所得到的轨迹出现三种情况。
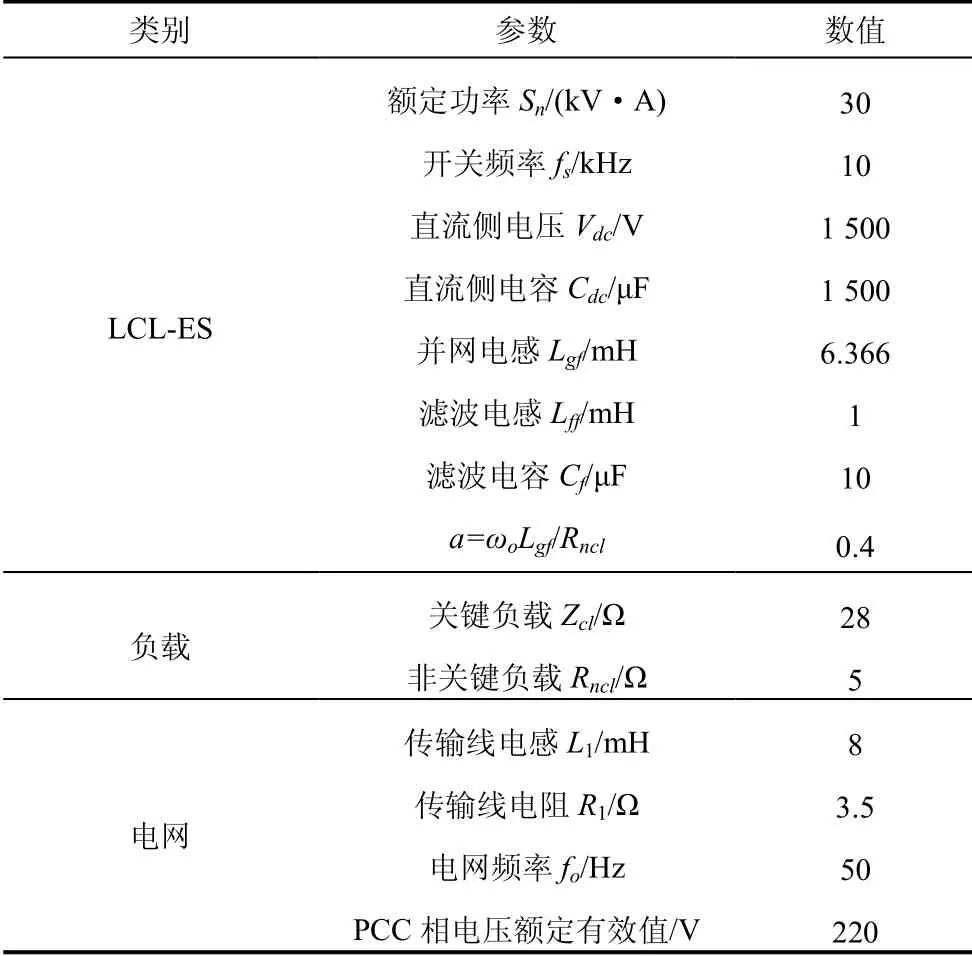
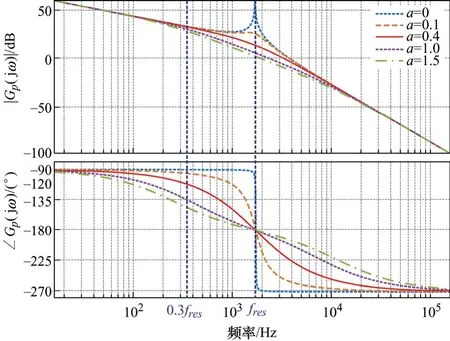
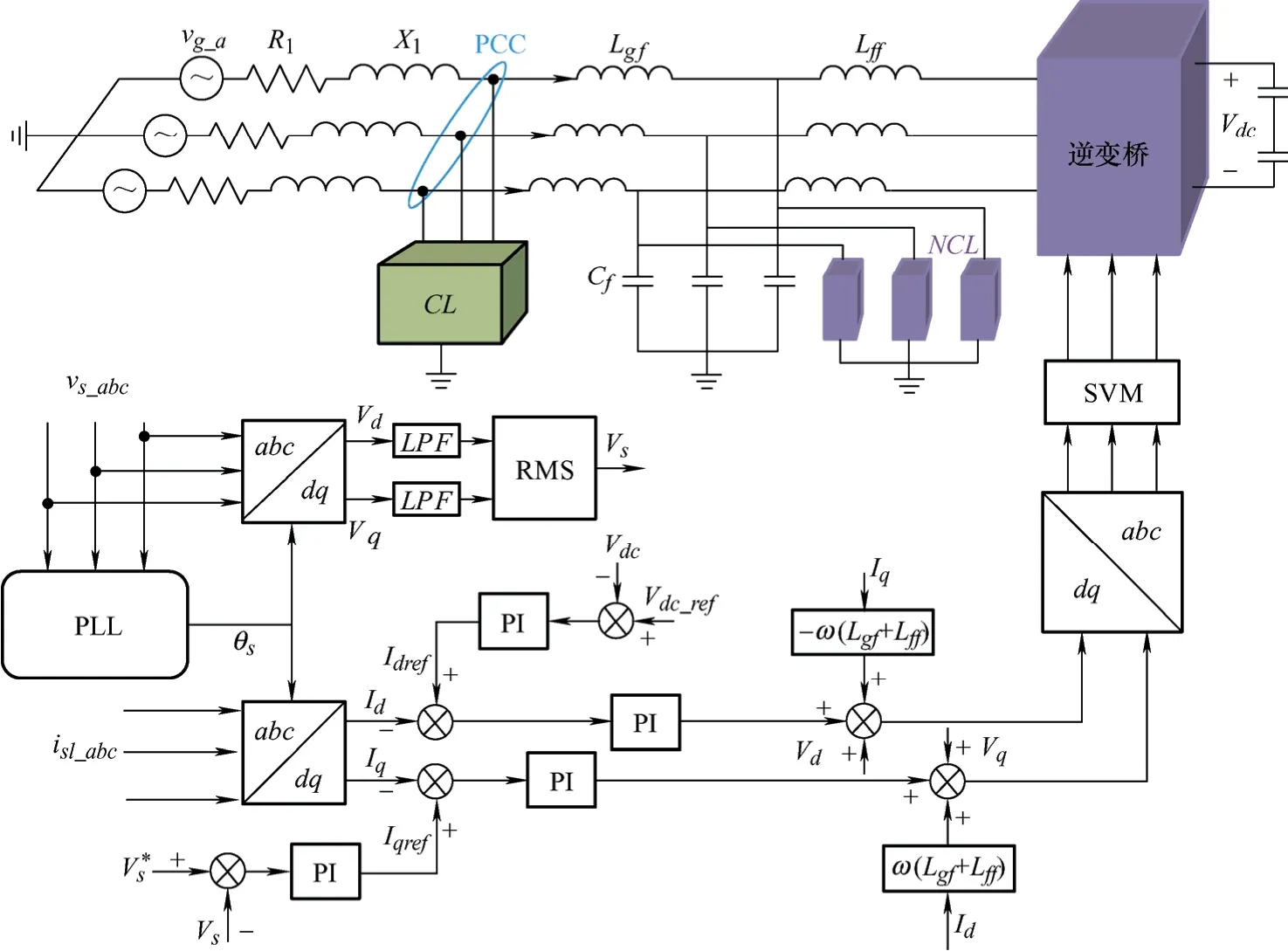
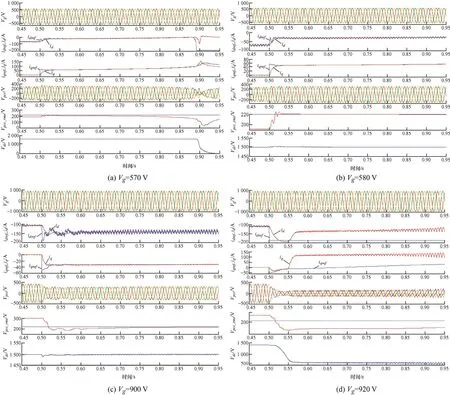
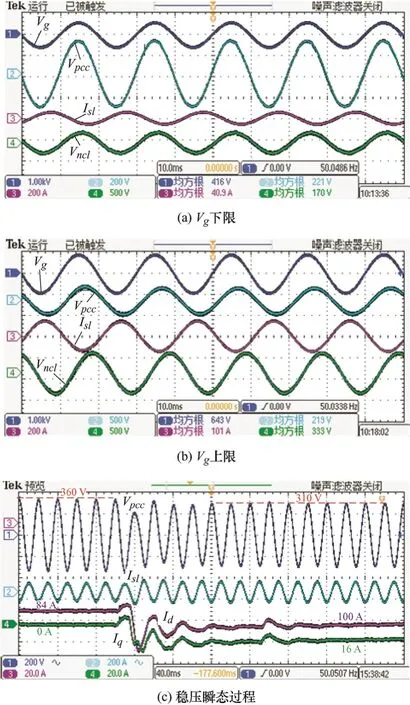
第一种情况,当|OC| 第二种情况,当Vg<|OC|或者Vg>|OD|时,不存在交点,这表明Vg的电压波动超出了LCL-ES的调节范围,PCC电压在此情况下无法稳定到目标值。 第三种情况,当Vg=|OC|或者Vg=|OD|时,只有一个交点,这意味着LCL型电力弹簧可以将PCC电压稳定在目标值,且仅存在唯一的平衡点,即为电压调节范围的临界点。根据式(24)确定 圆心O'和半径R后可以计算出网侧电压波动的上下限。 在网侧电压相量轨迹图上还具有两个特殊点e和f,两点均对应 =0θ,即LCL-ES的阻性工作点。线段ef将圆轨迹分为两部分:弧和对应,此时LCL-SL 工作于容性模式;对应,此时其工作于感性模式。理想情况下网侧电压波动上下限分别为|OO'|+R和|OO'|-R。但是为了避免两个平衡点可能给系统带来的不稳定性问题,需要重新计算网侧电压波动允许范围。实际上在Vs稳定时,LCL-SL的有功和无功取决于Isl的幅值和相位,因此图3中功率曲线单调单值弧线段和图4b中的单值单调弧线段是对应的。如图4b所示,随着Isl在弧线段上从j点运动到k点,Vncl也随之在上从M点运动到N点。根据式(23),Vncl的运动轨迹映射到图5中的网侧电压波动范围为 利用几何关系可以先计算出图4b中Vncl的轨迹,再根据式(23),可以得到如下结果 根据图5,|Om|和|On|中的较大值对应网侧电压波动的上限,而下限为|OO'|−R。可见在已知电网参数的情况下,网侧电压波动范围与a显著相关,同时NCL的大小也有一定影响,当a和Rncl越小时,网侧电压波动允许范围越大。根据理论分析结果,在已知电网和LCL-ES参数时,可以衡量LCL-ES的网侧电压波动范围或稳压能力,以避免网侧电压波动越限造成稳压失灵。 由于LCL-ES中并网侧电感Lgf的大小关系到其功率补偿特性和稳压运行范围,故LCL-ES的滤波器参数设计不同于常规的LCL滤波器[19-20],需要重新设计。对于LCL滤波器的谐振尖峰问题,常用的阻尼方法可以分为无源阻尼和有源阻尼两种。常见的有源阻尼方法有通过滤波电容电流反馈构成与电容串联的虚拟电阻来抑制谐振尖峰。常用的无源阻尼措施有给滤波电容串并连电阻或电感,这种方法不需要额外的传感器,不会增加控制回路设计的复杂度和回路之间的干扰,简单有效,但是由于损耗比较大而一般不被采用[21]。在本文LCL-ES应用中,NCL与滤波电容并联构成并联无源阻尼,其功率损耗是合理且必需的,这实际上克服了无源阻尼的劣势。 首先做一些合理的假设:NCL为纯电阻负载,即Zncl=Rncl;PCC处电压三相平衡(三相情况时),即仅考虑正序电压分量;忽略所有无源元件的等效串联电阻和寄生参数,即在谐振阻尼最恶劣情况[22]。进行稳定性分析和高频域分析时,PCC处可视为直接接地(Vs(s)=0),得到如图6所示的LCL-ES模型。 图6 LCL-ES模型 从调制信号Vm(s)到Isl(s)的传递函数Gp(s)为 式中,KPWM为VSI的调制增益,谐振频率ωres(=2πfres)和阻尼系数ζ分别为 根据式(28)和表1参数可以绘制出参数a不同取值下Gp(s)的频率响应,如图7所示。 表1 设计参数 图7 LCL滤波器的伯德图 显然系统的带宽或截止频率fc不能超过或接近谐振频率fres,否则会造成系统不稳定。一方面,采样和调制延迟效应也会限制系统的控制带宽,为了保证系统有足够的相角裕度,fc不能超过0.3ωres[22]。另一方面,为了保证系统对基波的良好跟踪性能,fc应远高于基波频率fo。同时为了抑制开关谐波,开关角频率fs应大于两倍fres。总的来说,系统的带宽应满足如下关系 确定了系统的带宽要求后,LCL-ES的设计可按照以下步骤进行。 (1) 确定非关键负载Rncl和参数a的大小。从功率补偿角度看,Rncl与功率基准值Sn密切相关,主要决定了LCL型电力弹簧有功补偿的范围,而参数a能够显著改变其补偿曲线的特性从而影响智能负载有功和无功参与的比例。从稳态运行范围角度看,Rncl和a都能够影响其所允许的网侧电压波动范围,但是主要由a决定。 (2) 接下来根据式(31)确定谐振频率fres,开关频率fs和截止频率fc。确定了谐振频率后根据式(29)和式(30)可以确定无源元件的大小。 为了使LCL-ES运行于纯无功补偿模式且能够保证PCC电压稳定,本文所设计的控制策略有两个目标:LCL-ES直流侧电压的稳定和PCC电压有效值的稳定。如图8所示为在同步旋转(dq)坐标系中,采用典型的电流控制型电压源逆变器的控制框图。图8中的锁相环(PLL)提供PCC电压vs_abc的相位信息,用以实现abc和dq坐标系之间的转换。系统采用两个PI控制器分别根据电流给定值Idref和Iqref对实际Id和Iq进行调节,来实现对LCL-SL的有功和无功功率的控制。为了稳定逆变器直流侧电容的端电压Vdc,使LCL-ES运行在纯无功补偿模式,电流有功分量给定值Idref由直流侧电压外环给定。PCC电压外环则可以根据PCC处电压有效值和参考值的误差来调节无功分量给定值Iqref。同时图8所示的控制结构有一个电网电压前馈环节,PCC电压转换为dq轴分量Vq和Vd后,作为前馈控制与电流内环控制器输出信号进行了叠加,以提高控制器的动态性能。为了进一步提高PI控制器在系统中的性能,系统采用了交叉耦合项±ω(Lff+Lgf)。控制器参数设计可以参考文献[22],控制器的离散化和最优化可以参考文献[23],在此不再赘述。 图8 LCL-ES控制系统结构 为了验证LCL-ES的稳压效果及其稳态运行范围,本文首先基于Matlab/Simulink平台和图8系统搭建了仿真模型,具体参数如表1所示。然后基于PLECS/RT-Box平台进行了硬件在环试验验证。 根据表1中数据和第2节理论及式(24)~(27)可以计算出预期的网侧电压幅值Vg波动下限为583.5 V,上限为901 V。在仿真试验中网侧电压Vg设置了4组电压等级:① 570 V;② 580 V;③ 900 V;④ 920 V。其中②③为边界验证,①④为越下限和上限验证。每一组仿真时长为1 s,在0.5 s时LCL-ES的稳压功能被激活,其目标是使PCC电压有效值稳定在220 V。如图9所示,各组仿真结果中所观测的数据依次为:网侧三相电压Vg;d轴电流参考值idref和实际值id;q轴电流参考值iqref和实际值iq;PCC三相电压Vpcc;PCC相电压有效值Vpcc_rms;LCL-ES直流侧电压Vdc。需要注意的是仿真中的电流参考方向为从LCL-SL注入PCC。 从图9仿真结果可以看出:① 当网侧电压Vg在电压等级②③对应的边界电压范围内,系统均能通过LCL-ES调节使PCC电压达到标准电压220 V附近,其中电压等级②对应的电网欠压情况下LCL-ES运行于容性模式而在电压等级③对应的电网过压情况下运行于感性模式;②Vg低于下限①或高于上限④时,LCL-ES启动后不久便发生失稳现象,即超出其调节能力范围。上下限的仿真结果和理论计算结果相当接近,足以验证稳态运行范围理论分析的有效性。从功率补偿角度来看,仿真试验②③组在稳态以后的所对应的有功无功功率分别为(0.45, -0.88) p.u.和(2.25, 0.514) p.u.,在图3b中的功率曲线上分别标记为点②③,这与LCL-ES的功率特性一致。 图9 不同网侧电压下LCL-ES的仿真结果 基于PLECS/RT-Box平台搭建了如图8所示的电力系统模型,其中逆变器采用中点钳位型三电平逆变器并使用空间矢量调制法。如图10a、10b所示为稳态试验结果,四通道示波器所采集的信号依次为:网侧电压Vg(a相),PCC电压Vpcc(a相),LCL-SL电流Isl和NCL的端电压Vncl(a相);图10c所示为瞬态试验结果,所采集信号依次为:Vpcc(a相)、Isl(a相)、Isl的d轴分量Id和q轴分量Iq。 如图10a所示,网侧电压Vg有效值为416 V(幅值为588 V)接近其下限,PCC电压有效值仍能稳定在221 V。此时LCL-SL工作在容性模式,NCL的端电压Vncl=170 V有效值远低于其额定值220 V,LCL-SL向PCC注入有功功率和感性无功将PCC电压从欠压状态抬升到额定值。同理如图10b所示,网侧电压Vg有效值攀升到643 V(幅值为909 V)已经略超过理论上限,PCC电压有效值仍稳定在219 V。此时LCL-SL略呈感性,近似为阻性模式,NCL的有功功率为额定值的2.29倍,从PCC吸收多余的有功功率从而将PCC从过压状态拉回额定值。图10c所示为LCL-ES启动的瞬态过程:LCL-ES启动前电网处于过电压状态,PCC相电压幅值为360 V;LCL-ES启动后经过5至6个基波周期,PCC相电压幅值稳定为310 V,Id从84 A增大到100 A,Iq从零增大到16 A,LCL-SL的有功功率和感性无功增大。试验结果和仿真结果一致,同样验证了LCL-ES实现需求响应并稳定PCC电压的有效性以及稳态运行范围分析结果的正确性。 图10 LCL-ES的试验结果 本文基于一种新型电力弹簧——LCL-ES,从功率补偿范围和网侧电压波动范围角度分析了其的稳态运行范围。以纯无功补偿模式为例,LCL-ES的功率补偿范围比传统的串联型ES更加大,功率补偿特性更加灵活。利用几何方法结合相量图,本文分析了LCL-ES的网侧电压波动范围并给出其波动上下限的解析解。利用本文的分析结论可以掌握LCL-ES的功率补偿范围和网侧电压波动范围,避免LCL-ES工作时出现越限失灵,可用于指导LCL-ES在电网稳压和功率补偿方面的设计。
5 参数设计
5.1 主电路
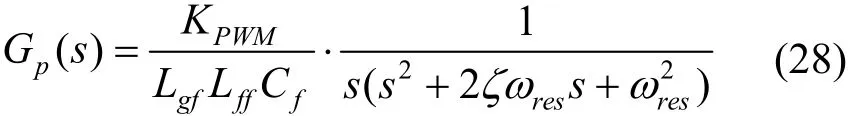
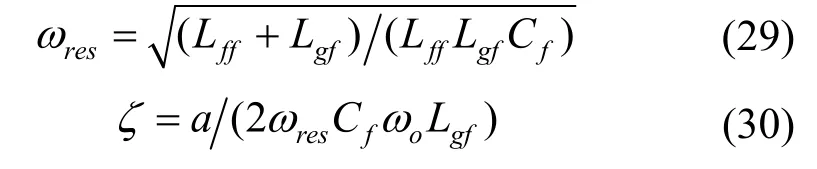
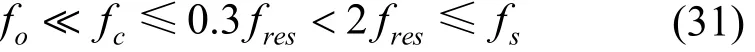
5.2 控制器
6 仿真和试验验证
6.1 基于Matlab/Simulink仿真验证
6.2 基于PLECS/RT-Box试验验证
7 结论
