弱电网下基于模型预测控制的NPC三电平LCL型并网逆变器谐振抑制方法研究*

丁金勇 吕建国 徐炜基 孙 状

(南京理工大学自动化学院 南京 210094)

1 引言

近年来，随着光伏、风电等新能源发电的迅速发展，新能源并网技术的研究成为热点[1]。由于电压型光伏并网逆变器具有功率因数可控、电流正弦度高等优点，在智能电网、光伏发电等多个领域应用的十分广泛[2]。远距离输电以及大量非线性负载广泛被应用，电路中线路阻抗无法被忽略，使得电网稍呈现出感性，这种情况被定义为弱电网[3-5]。传统控制策略下的逆变器并网电流将会畸变，使逆变器和电网的运行情况恶化。因此，研究弱电网条件下并网逆变器的控制方法具有重要的现实意义。目前，并网逆变器控制技术包括：直接功率控制(Direct power control，DPC)、滞环控制(Hysteresis control)和模型预测控制(Model predictive control，MPC)等[6-9]。

模型预测控制通过建立系统预测模型，利用系统模型来预测系统在未来一段时间内的动态行为，在此基础上对针对系统所设计的优化目标函数进行滚动求解最优控制量，具有设计简单、动态响应速度快、多变量灵活控制、易于处理非线性约束等优点[10-13]，并且伴随着数字控制芯片处理能力的提高，模型预测控制在电力电子功率变换等领域得到了广泛应用[14-16]。对于LCL滤波器存在的谐振问题，无源阻尼方法通常在滤波电 容侧并联或串联阻尼电阻，达到谐振抑制的效 果[17-18]，然而该方法在系统运行时会产生额外的功率损耗，因此相关专家学者提出一种改变系统控制结构的有源阻尼方法。文献[19-20]对线性控制方法下的有源阻尼方法进行了研究，通过电容电流反馈，实现了对系统谐振频率的抑制。文 献[21-22]通过对三相并网逆变器的电网电压全前馈策略进行分析，对系统存在的谐振进行了抑制。目前已有文献对模型预测控制方法下并网逆变器的谐振问题进行了研究。文献[23]基于两电平三相LCL型逆变器采用了有源阻尼算法与滞环模型预测控制方法，但需要较为复杂的参数设计；文献[24]采用模型预测控制方法，针对LCL滤波器存在的谐振问题，提出了MPC-i1i2uc谐振抑制策略，分析对比了几种谐振抑制方法的控制效果。

上述文献从多个方面对传统线性控制方法对谐振抑制策略进行了研究，但涉及模型预测控制方法下的谐振抑制策略研究较少，本文对弱电网条件下基于模型预测控制方法的NPC三电平LCL型逆变器谐振抑制策略进行研究，适应一定弱电网阻抗的变化，实现并网电流正弦和中点电压波动抑制的控制目标。

本文建立了弱电网条件下NPC三电平LCL型并网逆变器输出电流和直流侧中点电压的预测模型，研究了一种模型预测控制方法下适用于弱电网的系统谐振抑制策略，实现了在弱电网阻抗变化时对系统谐振的抑制。最后通过并网试验对本文所研究谐振抑制策略进行了验证。

2 弱电网下NPC三电平LCL型并网逆变器预测模型

2.1 NPC型逆变器离散化模型

图1为弱电网下NPC型三相三电平LCL并网逆变器的电路结构示意图，图1中Vdc为直流侧电压，vc1和ic1分别为直流侧电容C1的电压和电流，vc2和ic2分别为直流侧电容C2的电压和电流，io为直流侧电容中点电流，i1a、i1b和i1c为逆变器侧输出电流，uca、ucb和ucc为交流侧电容电压，i2a、i2b和i2c为并网电流，L1a、L1b和L1c为逆变器侧三相滤波电感，R1a、R1b和R1c为逆变器侧电感寄生电阻，Cfa、Cfb和Cfc为交流侧三相滤波电容，L2a、L2b和L2c为并网侧三相滤波电感，R2a、R2b和R2c为并网侧电感寄生电阻，Lga、Lgb和Lgc为三相弱电网等效电感，Rga、Rgb和Rgc为三相弱电网等效电阻。取直流侧电容C1=C2=C，直流侧平衡时电容电压vc1=vc2=Vdc/2，三相逆变器侧滤波电感感值L1a=L1b=L1c=L1，三相滤波电容容值Cfa=Cfb=Cfc=Cf，三相并网侧滤波电感感值L2a=L2b=L2c=L2，三相弱电网等效电感感值Lga=Lgb=Lgc=Lg。

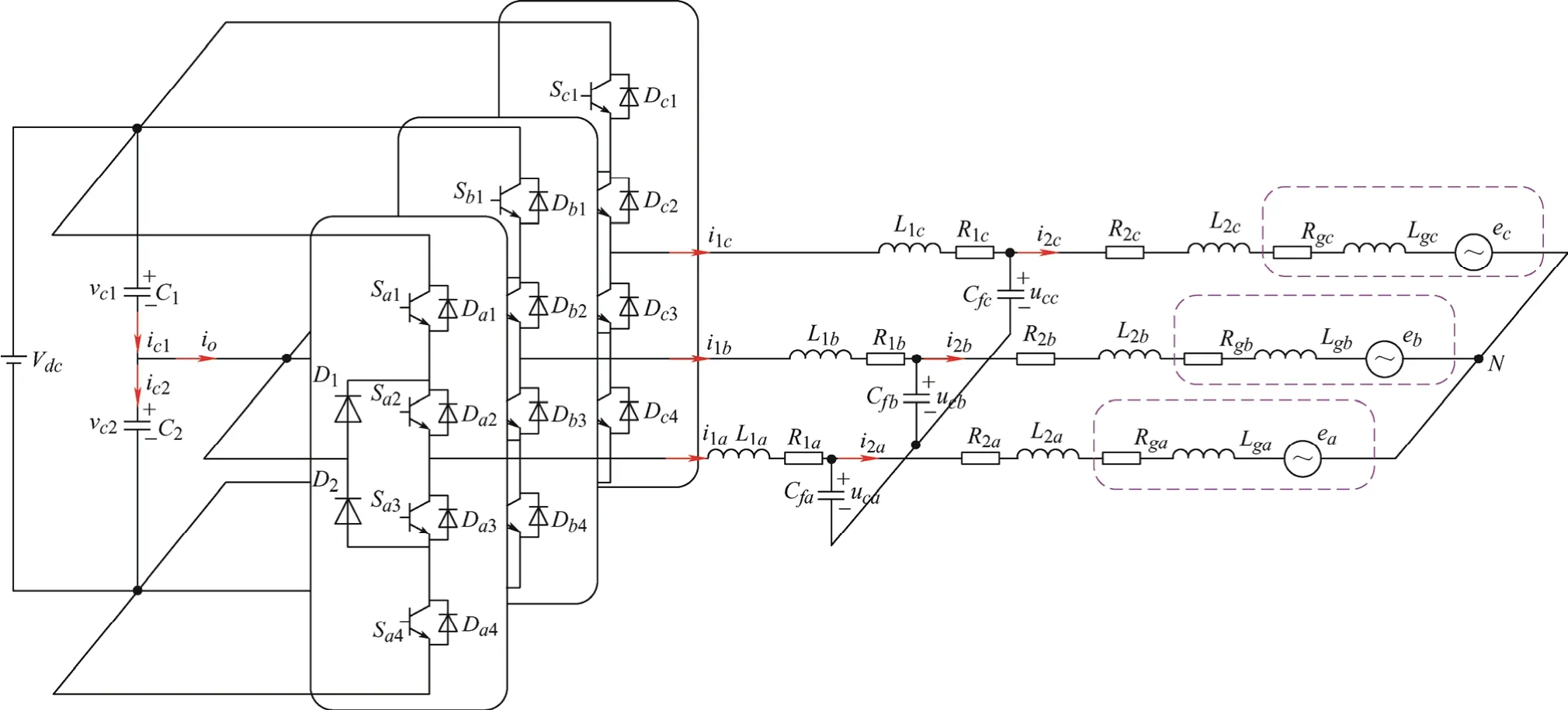
图1 弱电网下NPC三电平LCL型并网逆变器主电路

定义相开关函数为

式中，i=a、b、c，Si=1记为状态P，Si=0记为状态O，Si=−1记为状态N。

逆变器交流输出侧(a、b、c)相对直流侧中点(O)的电压

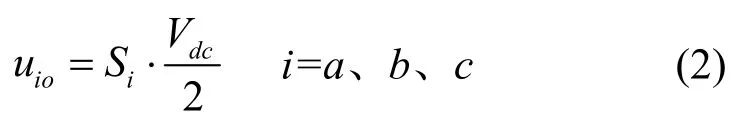
三相三电平逆变器有33=27个开关状态，对应于αβ坐标系下27个输出电压矢量。

由基尔霍夫电压定律得逆变器侧电压平衡方程(电流参考方向如图1所示)

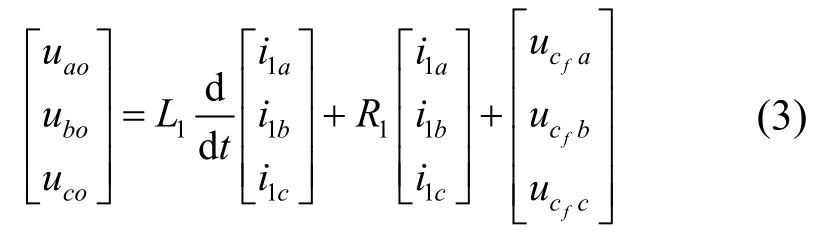
对式(3)进行Clark变换，得到αβ坐标系下逆变器输出侧电压平衡方程为

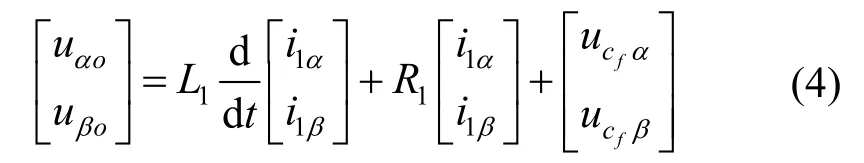
取采样周期为Ts，采用一阶前向差分法对式(4)进行离散化，得到αβ坐标系下逆变器侧电流i1的离散数学模型为

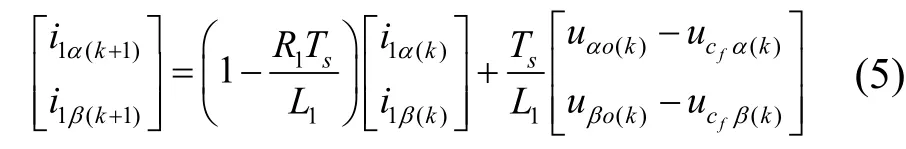
式中，i1α(k)、i1β(k)为第k个采样周期三相逆变器侧电流经过Clark变换后的值，uαo(k)、uβo(k)为第k个采样周期逆变器输出的不同电压矢量在αβ坐标系下的坐标值，ucf α(k)、ucf β(k)为第k个采样周期交流侧电容电压经过Clark变换后的值，i1α(k+1)、i1β(k+1)为αβ坐标系下第k+1个采样周期逆变器侧电流预测值。

由基尔霍夫电流定律，得到直流侧中点(O)的电流平衡方程[25]

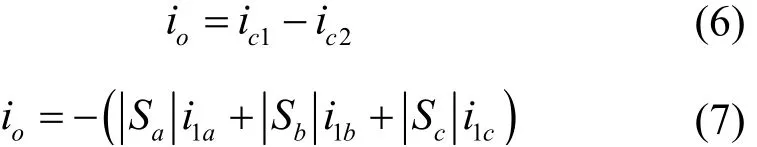
电容C1=C2=C电流方程为

令直流侧中点电压Δvc=vc1−vc2，同时将式(6)、(8)、(9)代入式(7)，可得

采用一阶前向差分对式(10)进行离散化，abc坐标系下直流侧中点电压的离散数学模型为

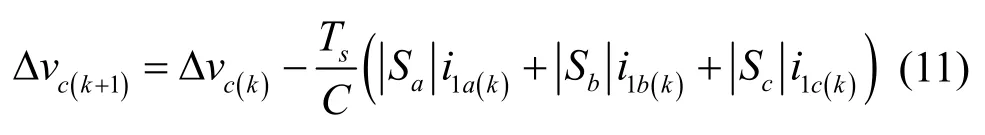
式中，Δvc(k)为第k个采样周期直流侧中点电压采样值，Δvc(k+1)为第k+1个采样周期直流侧中点电压反馈值。

2.2 MPC-i1uc_f谐振抑制策略

本文从预测模型角度出发，利用二阶广义积分器(Second order generalized integrator，SOGI)获得电容电压基频分量，送至预测模型，消除了谐振分量对系统的影响，继而实现谐振抑制。本文提出MPC-i1uc_f方法，避免了复杂的阻尼参数设计，具体分析如下。

忽略电感的寄生电阻，由基尔霍夫电路定律得，图2对应的数学模型为

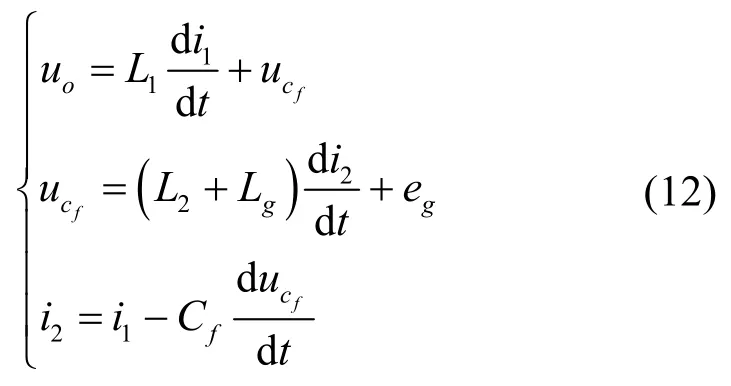
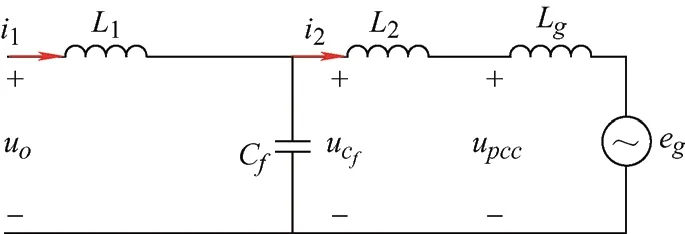
图2 LCL滤波器等效电路

当控制逆变器输出侧电流i1时，系统会存在谐振频率fres

理想情况下，MPC的传递函数为1，即GMPC(s)=1；则i1至i2的控制框图如图3所示。

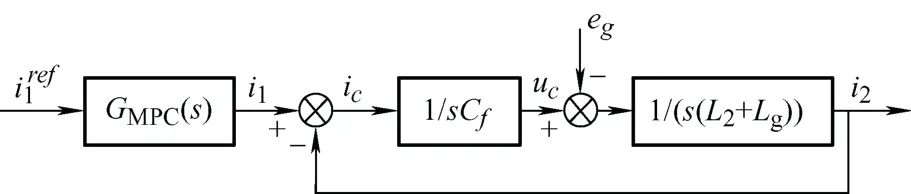
图3 LCL系统无阻尼控制框图

系统i1至i2的传递函数为

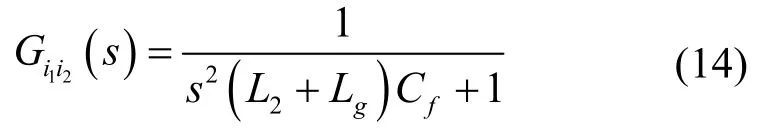
由式(14)可得i1至i2的伯德图，如图4所示。

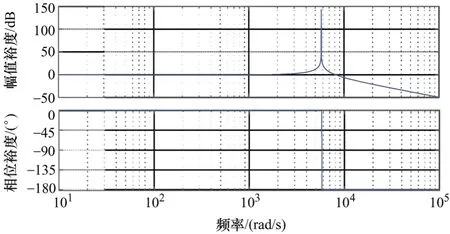
图4 无阻尼系统伯德图

通过图4中i1至i2的伯德图分析得到，在系统谐振fres处增益无穷大，相位会出现−180°跳变，对应一对右半平面的闭环极点，导致并网逆变器不稳定。这种现象是由于较低的系统阻尼造成的，因此需要在系统中增加阻尼项。

将系统分为高频部分和基频部分，且基频部分不存在谐振问题，只需要对系统的高频部分添加阻尼项，采用电容两端并联电阻的虚拟阻抗方法，去进行阻尼设计。本文在模型预测控制方法下基于有源阻尼算法提出采样电容电压基频分量的谐振抑制方法，来实现对系统谐振的抑制。此种方法仅需采样得到电容电压基频分量，无需复杂的阻尼参数设计，且阻尼效果良好。

首先，假设系统中变量分为高频部分和基频部分，即

式中，x为系统变量实际值，x−f为系统变量基频分量，x−h为系统变量高频分量。

在采用MPC-i1uc_f方法时，式(5)变为

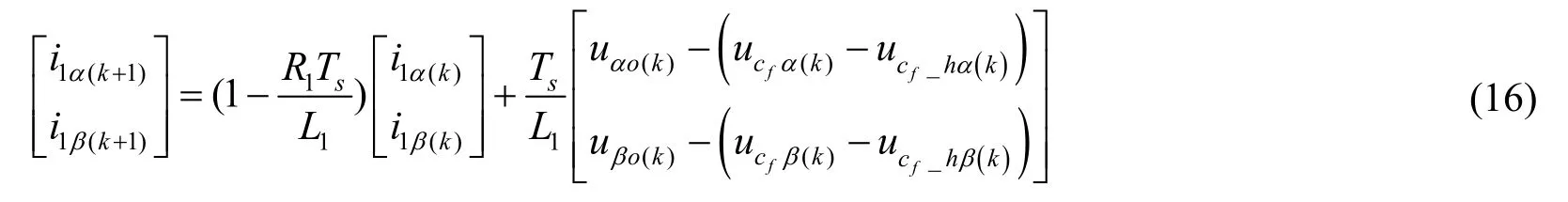
由图5可知，在含有谐振分量的高频部分进行阻尼设计

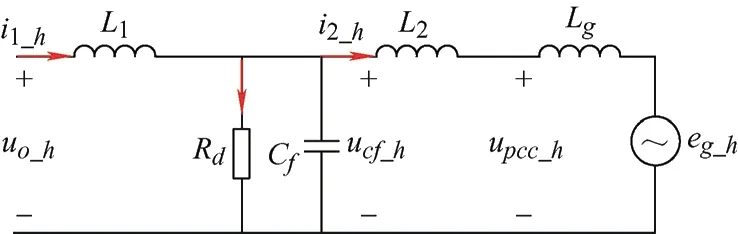
图5 电容两端并联电阻的等效电路

i1_h至i2_h的控制框图如图6所示，其中参考值在高频模型中值为0。

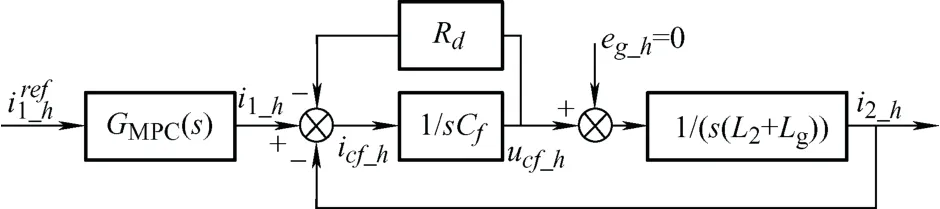
图6 加入虚拟阻抗的系统控制框图

系统i1_h至i2_h的传递函数为

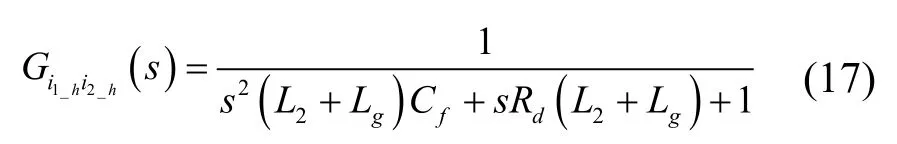
虚拟阻抗Rd的取值为Ts/L1，在弱电网阻抗Lg变化时加入虚拟阻抗的系统伯德图如图7所示。

图7为弱电网电感Lg=0.5 mH、1 mH和1.5 mH时系统的伯德图。通过图7中i1_h至i2_h的伯德图分析得到，在系统中加入阻抗项后，系统谐振得到一定的抑制，实现了阻尼的效果，并且在弱电网电感Lg变化时，依然能够实现较好的阻尼效果。

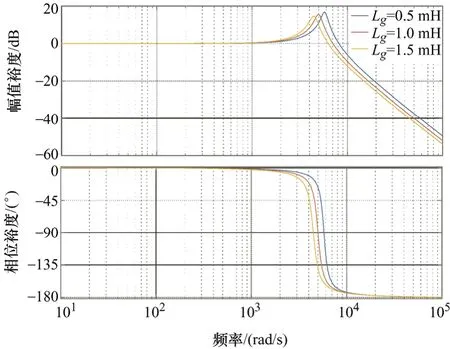
图7 加入虚拟阻抗的系统伯德图

又因在理想情况下GMPC(s)=1，故将图6进行等效变换，如图8所示。

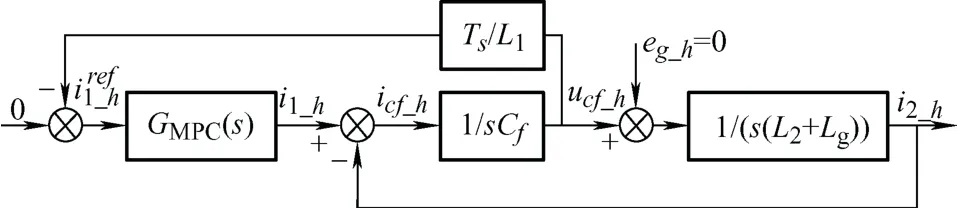
图8 加入虚拟阻抗的系统等效控制框图

由图8的等效框图可以发现，在MPC中采用有源阻尼时参考电流的高频分量变为

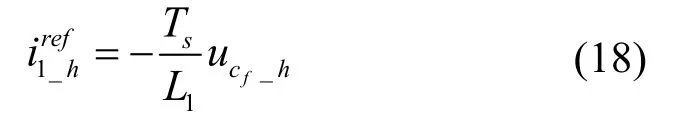
设k+1时刻电流i1(k+1)已跟踪参考电流，即，代入式(5)中并变换得

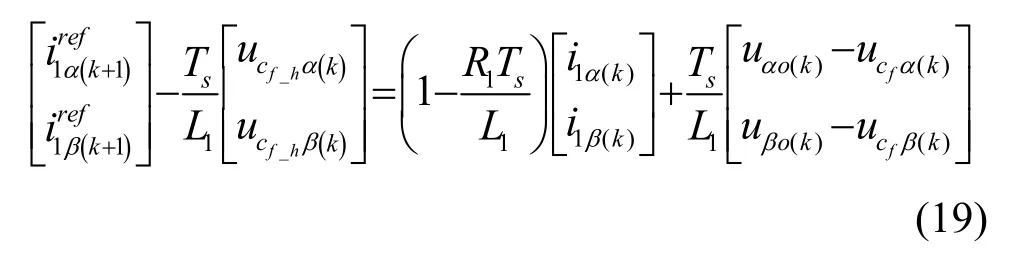
有源阻尼下的式(19)与所提出的采样电容电压基频分量方法一致，故MPC-i1uc_f策略可以对系统谐振抑制，避免了在模型预测控制中进行有源阻尼参数设计的复杂性。本文采用SOGI获取αβ坐标系下电容电压基频分量，SOGI结构框图如图9所示。

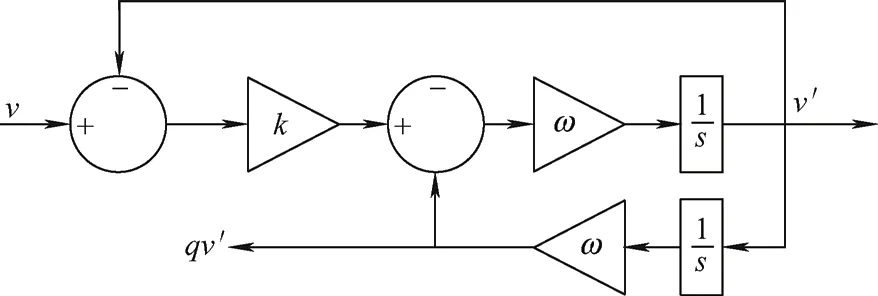
图9 SOGI结构框图

图9中，v′为输入信号v的基波分量，qv′为输入信号v滞后90°的基波分量。

二阶广义积分器的表达如式(20)所示

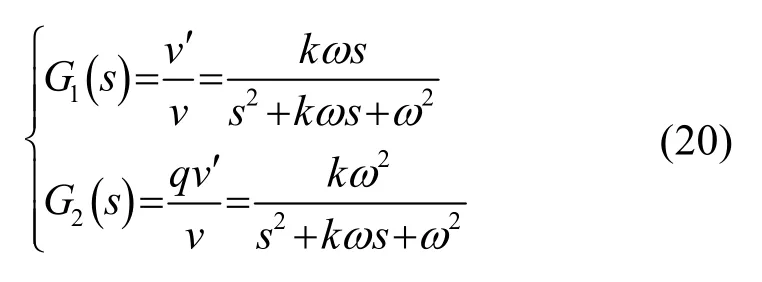
式中，ω为电网电压基波角频率，k表示增益，通常取值为0.707。

3 模型预测控制策略

根据式(1)可知a、b、c三相共有33=27个开关状态组合，有限集模型预测控制的矢量分布如图10所示。

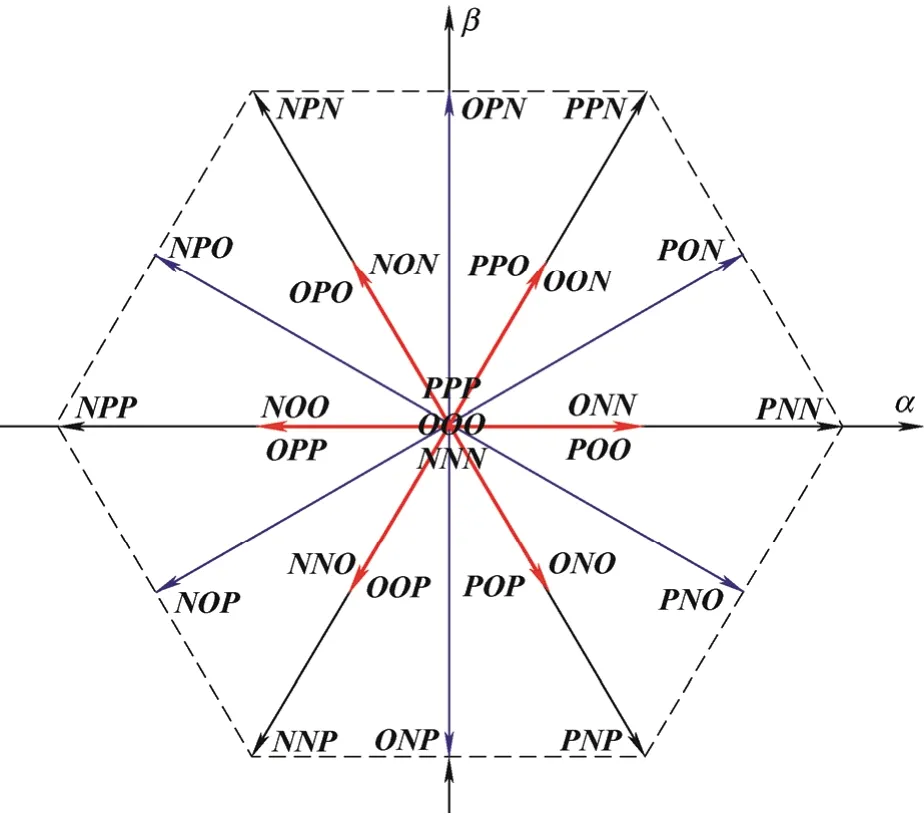
图10 αβ坐标系下三电平逆变器基本电压矢量空间分布图

有限集模型预测控制属于最优控制范畴，为选出最优的开关状态，需要定义与被控制变量相关的目标函数g作为最优选择的依据，使g最小的开关状态将被选作为最优开关状态Sopt，并在下一个采样周期开始时作用于逆变器。定义目标函数g如式(21)所示

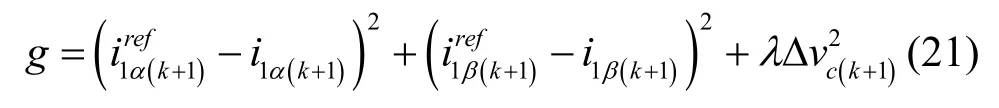
式中，前两项分别为αβ坐标系下的逆变器侧电流预测值i1α(k+1)、i1β(k+1)与逆变器侧电流参考值之间误差的平方值。当采样周期Ts较小，近似认为。第三项为直流侧中点电压差的平方值，λ为直流侧中点电压差权重系数。本文中，λ取值为10。

由于采样和计算所造成的延迟使得依据k时刻的采样值进行预测计算并输出最优开关矢量Sopt，并不能使(k+1)时刻的实际入网电流与给定入网电流之间的误差最小，造成电流纹波偏大等问题。因此，这种“先计算后输出”的方式不可避免地会造成实际的控制输出时刻发生延迟。为了消除延迟，对被控变量进行两步预测计算，其基本原理如图11所示。

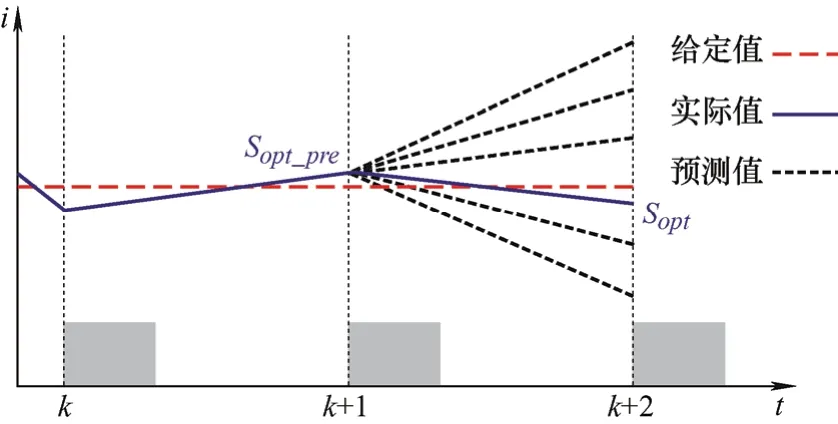
图11 采用延时补偿的模型预测控制策略

两步延迟补偿k+2时刻的i1和Δvc为

采用延时补偿后的目标函数如式(24)所示

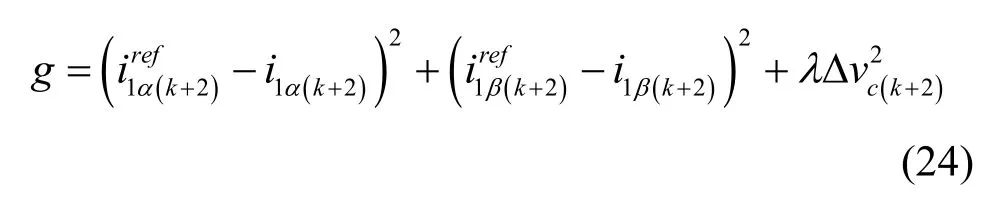
弱电网条件下NPC三电平LCL型并网逆变器的模型预测控制框图如图12所示，采样逆变器电流i1、电容电压uc及直流侧电压差Δvc，uc经过SOGI获得基频分量后，送至MPC计算模块，通过目标函数g寻优得到最优矢量Sopt。本文采用模型预测控制方法，并结合所提出的MPC-i1uc_f谐振抑制策略对系统谐振进行抑制。所述模型预测控制算法流程图如图13所示。

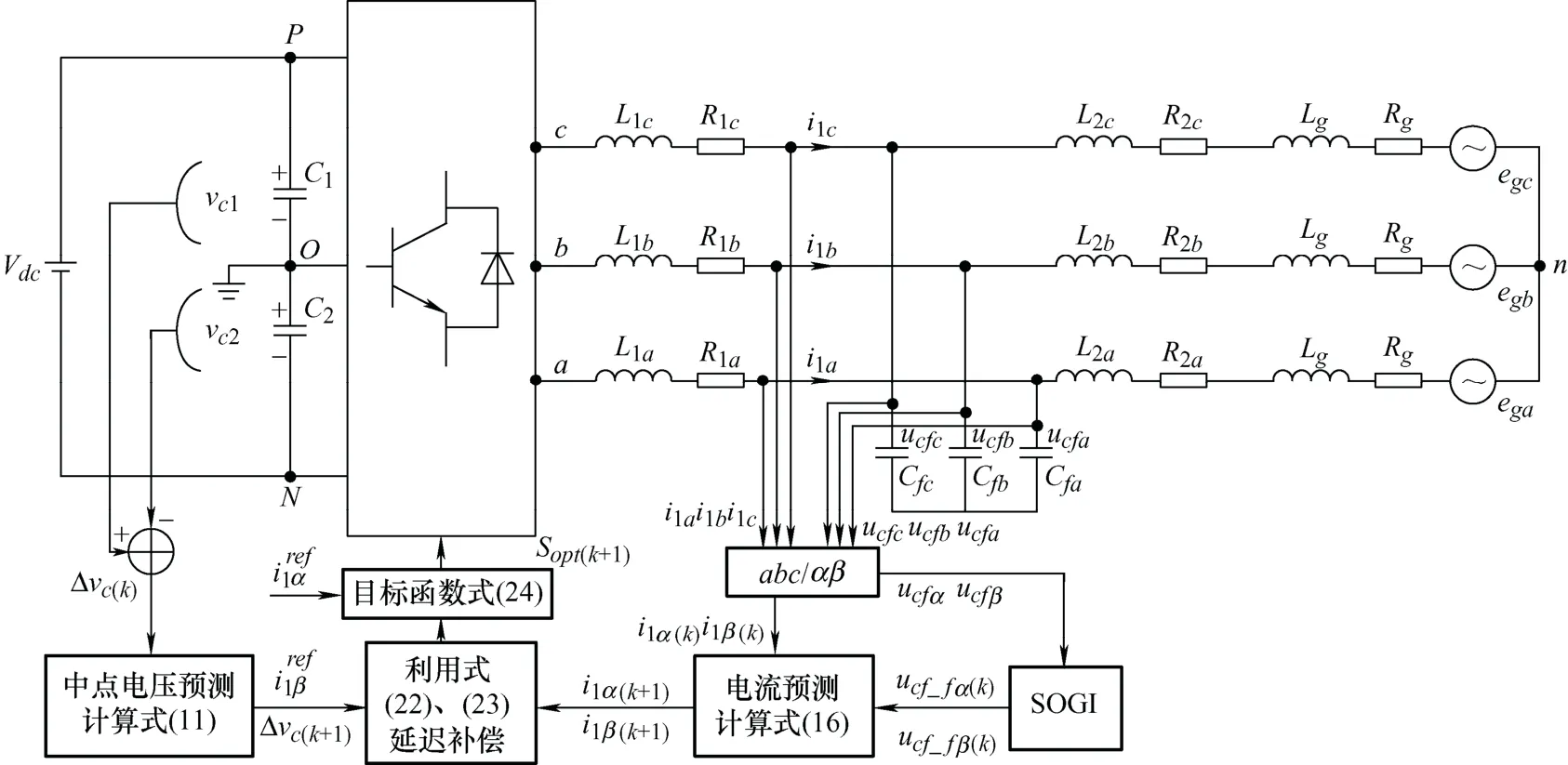
图12 弱电网下NPC三电平LCL型逆变器MPC控制框图

图13 MPC算法流程图

4 试验结果及分析

为了验证基于模型预测控制方法时所提出的MPC-i1uc_f谐振抑制策略在弱电网条件下的可行性，搭建了NPC三电平LCL型并网逆变器试验平台并对该方法进行了试验验证，试验具体参数如表1所示。

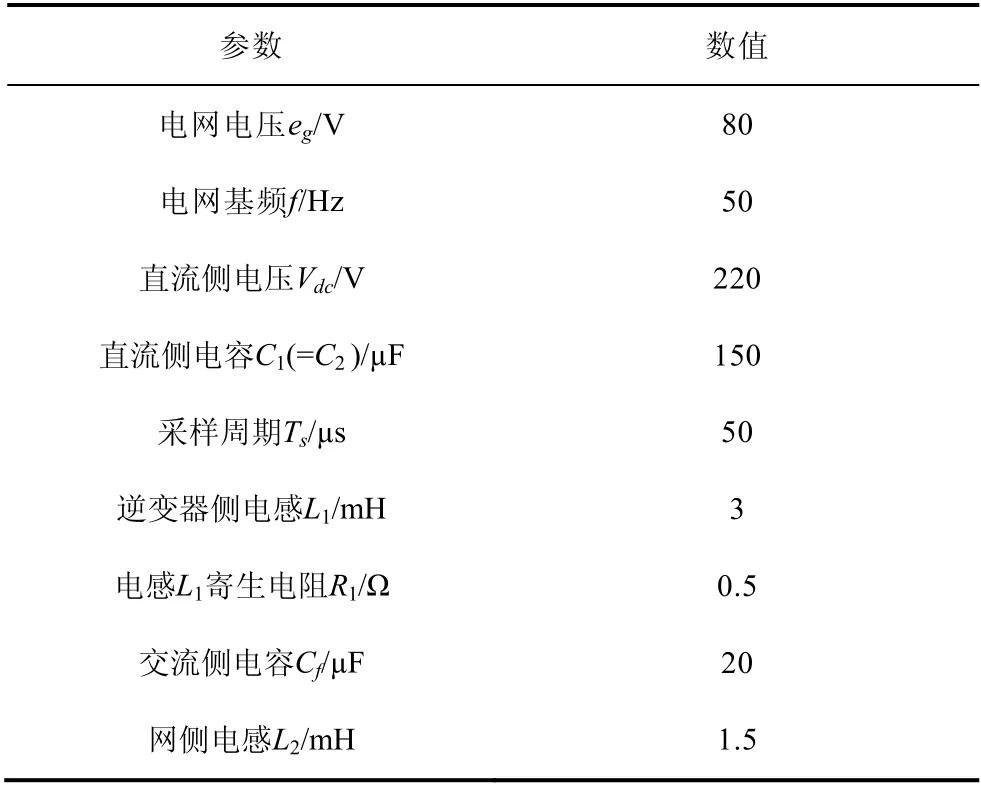
表1 试验参数

图14a～14c分别为无谐振抑制策略且弱电网电感Lg=0.25 mH时三相入网电流、A相入网电流THD图、直流侧中点电压的试验波形图，从图14可以看出，在不加谐振抑制策略时入网电流存在较大的谐振分量，不满足并网要求。

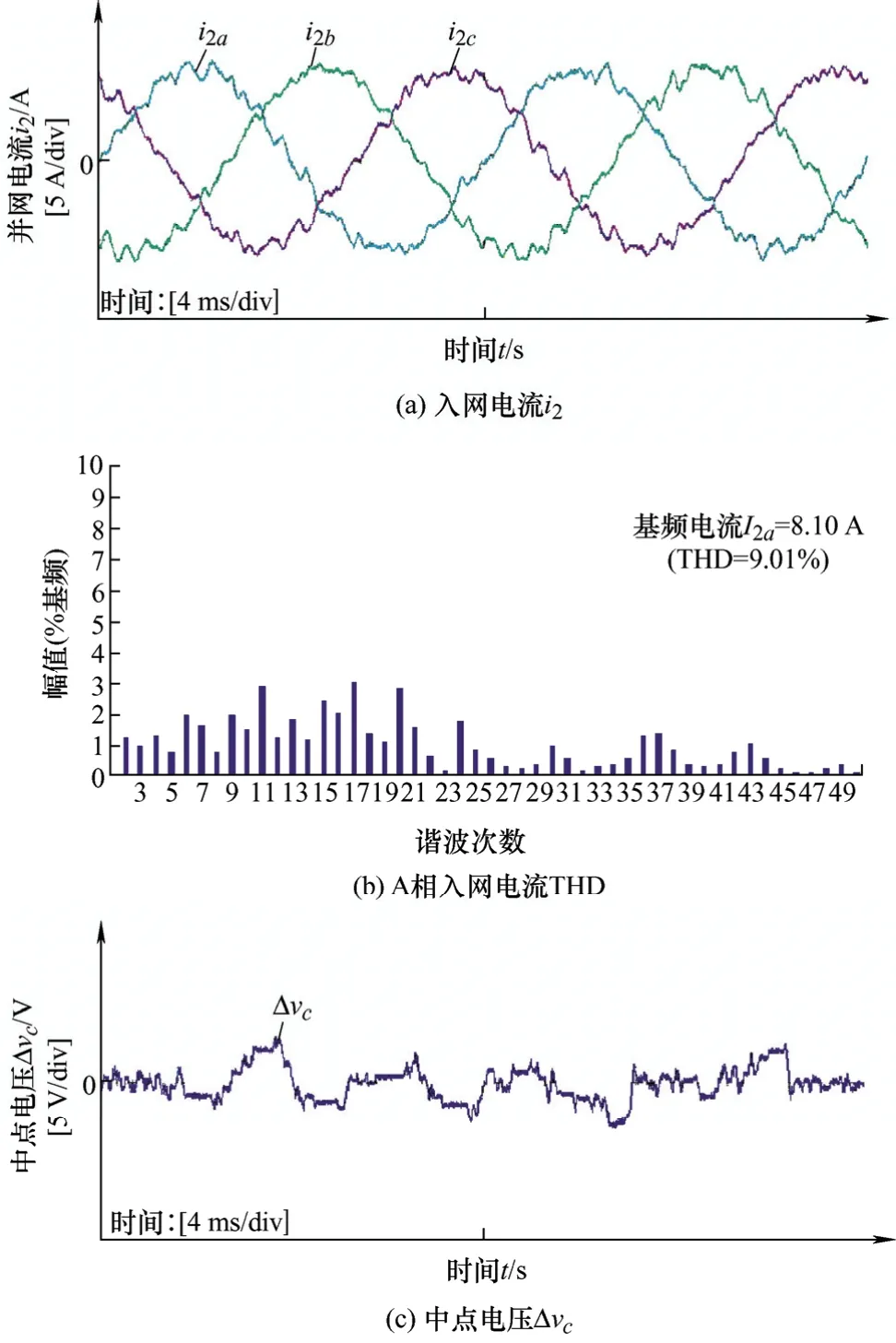
图14 未采用谐振抑制(Lg=0.25 mH)试验波形

图15a～15c分别为采用MPC-i1uc_f谐振抑制策略且弱电网电感Lg=0.25 mH时三相入网电流、A相入网电流THD图、直流侧中点电压的试验波形图，通过SOGI获得电容电压基频分量，送至预测模型中，实现系统谐振抑制。从图15可以看出，采用 MPC-i1uc_f谐振抑制策略时系统谐振得到抑制，满足并网电流THD小于5%的控制目标。

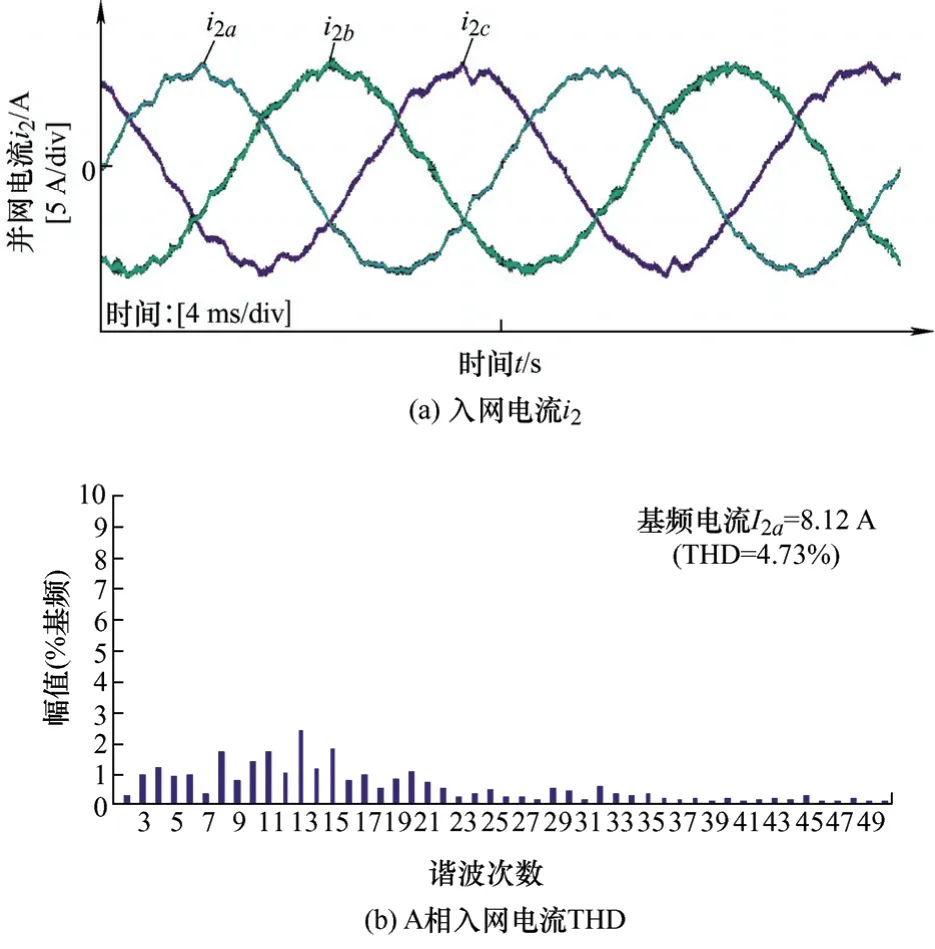
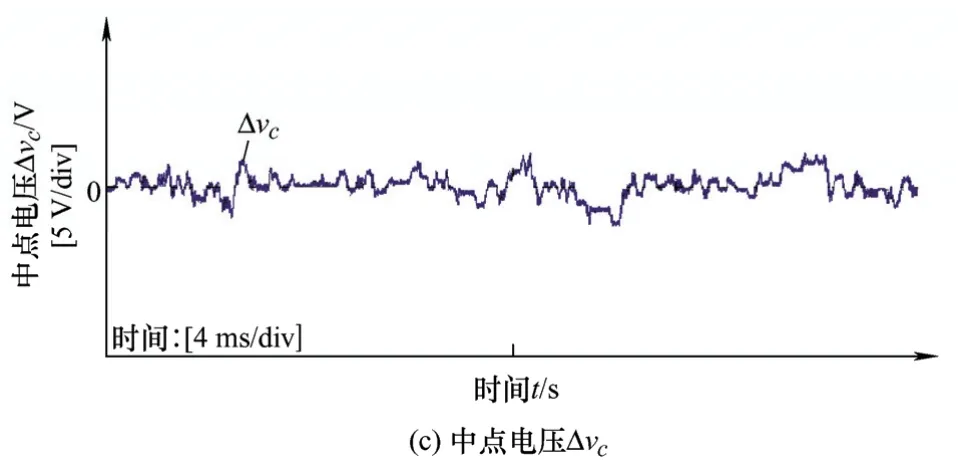
图15 采用MPC-i1uc_f谐振抑制(Lg=0.25 mH)试验波形

图16a～16c分别为采样电容电压基频分量弱电网电感Lg=1 mH时三相入网电流、A相入网电流THD图、直流侧中点电压的试验波形图，从图16可以看出，在弱电网阻抗变化时MPC-i1uc_f谐振抑制策略依然能够实现较好的谐振抑制效果。

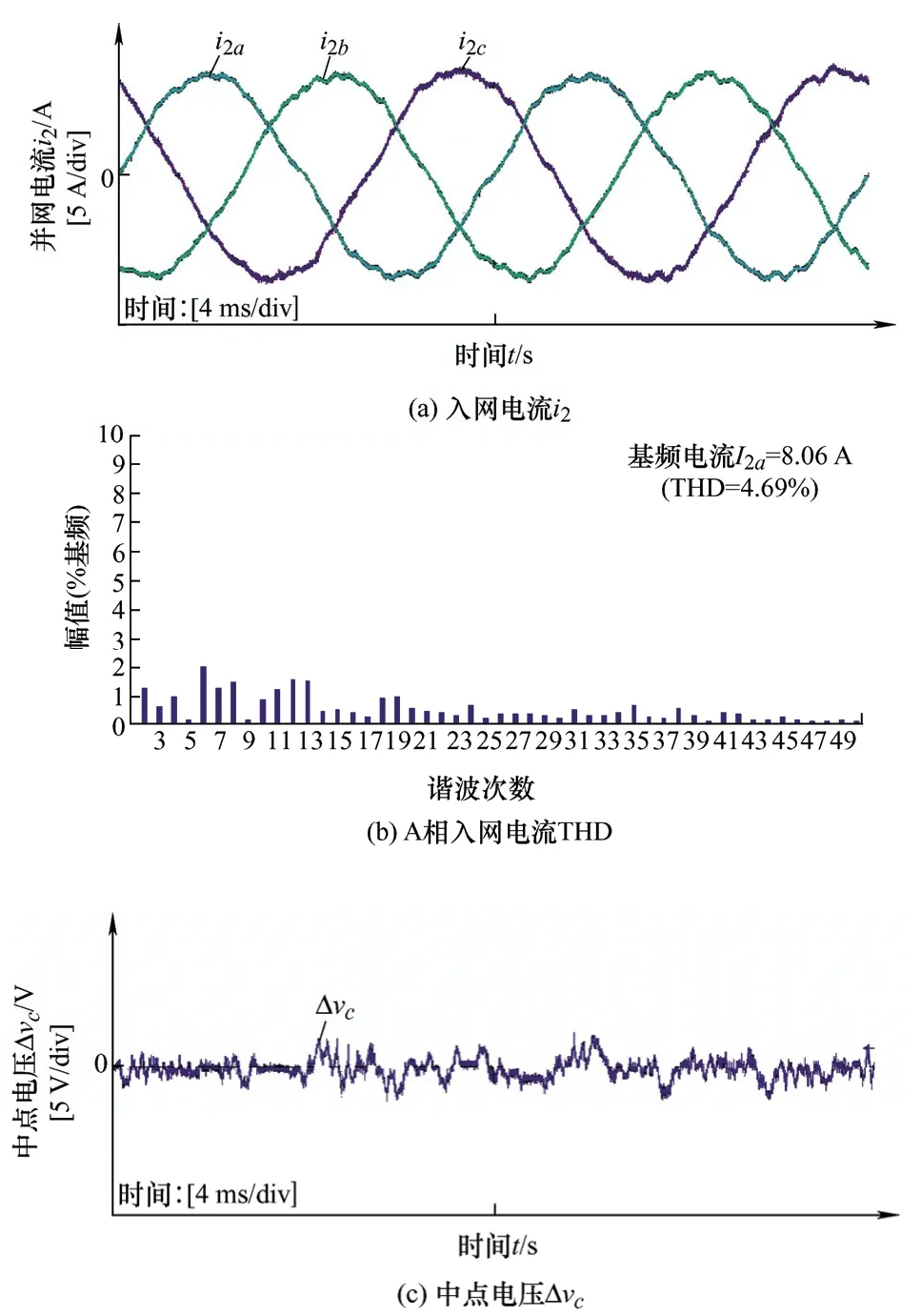
图16 弱电网Lg=1 mH试验波形

图17a～17b分别为弱电网电感Lg=1 mH时给定电流突变三相入网电流、直流侧中点电压的动态试验波形图，从图17可以看出，采用模型预测控制方法，动态响应快速，无超调，满足控制要求。

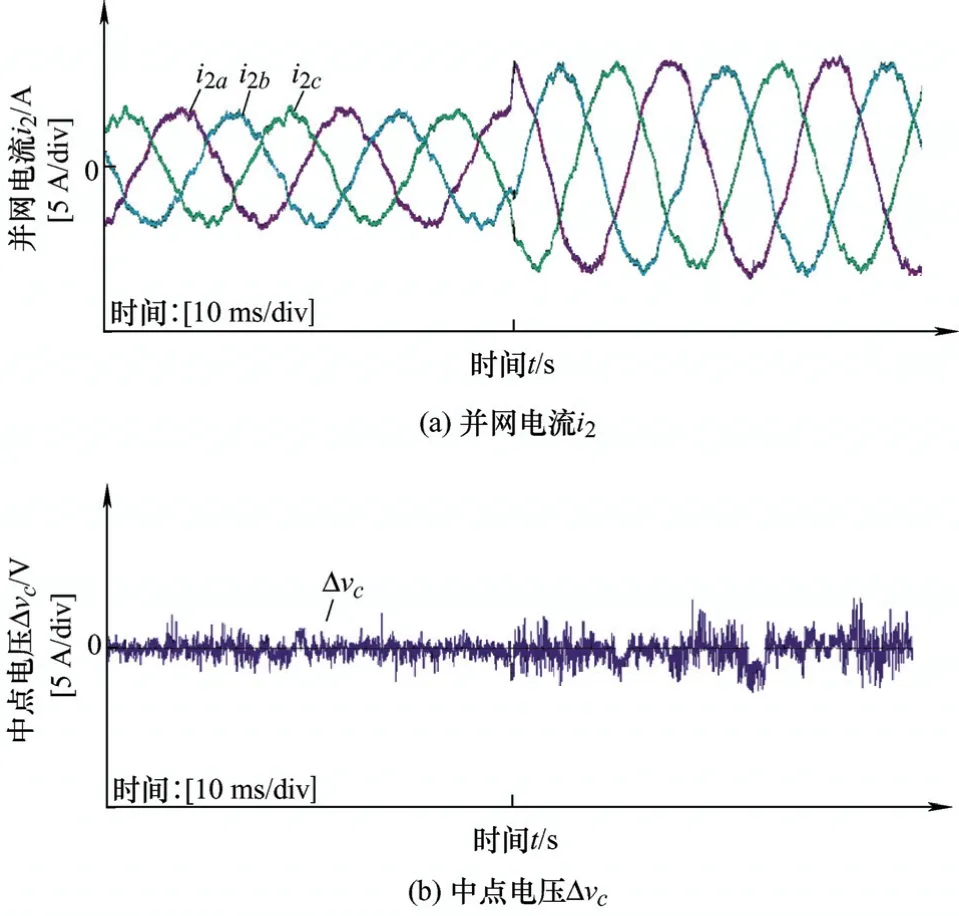
图17 动态试验结果

5 结论

基于模型预测控制方法，针对LCL型逆变器，本文分析了弱电网下LCL谐振对系统的影响，提出一种MPC-i1uc_f谐振抑制策略，理论分析与试验结果表明，本文所设计的方法能够抑制谐振，并且适应弱电网的变化。与现有MPC方法下的谐振抑制策略相比，本文设计的MPC-i1uc_f谐振抑制策略简化了阻尼参数设计，所需传感器数量少，便于工程应用。但需要指出的是，有限集模型预测控制开关频率不固定，因此对于模型预测控制算法的优化有待进一步的研究。