Numerical analysis of motional mode coupling of sympathetically cooled two-ion crystals*

Li-Jun Du(杜丽军) Yan-Song Meng(蒙艳松) Yu-Ling He(贺玉玲) and Jun Xie(谢军)

1China Academy of Space Technology(Xi’an),Xi’an 710100,China

2National Key Laboratory of Science and Technology on Space Microwave,China Academy of Space Technology(Xi’an),Xi’an 710100,China

3China Academy of Space Technology,Beijing 100094,China

Keywords: sympathetic cooling,coupled oscillations,secular motion,radio-frequency ion traps

1. Introduction

An important tool in the study of objective reality is the precise control and measurement of neutral, charged atomic and molecular quantum states because they play an important role in the discovery of new physical phenomena and in the testing of the fundamental laws of physics.[1]Through the use of the laser cooling and atom (ion) trapping techniques, the transition frequency of atomic and molecular systems can be controlled to a precision of 10-19,[2]which is the highest level of precision among all precision measurement techniques.The preparation and measurement of cold ion systems is typically performed using a red-detuned laser, which interacts with a closed cycling transition of the target ion to dissipate its kinetic energy and suppress the Doppler effect.This ensures that the quantum states of the ions are coherent and ready for precision measurements. However,many candidate ions that may be used for the development of precise frequency standards or probing the time variations of the fine structure constant[3-7]are difficult to cool, owing to the lack of cycling transitions or suitable lasers. This makes precise measurements of their transition lines impossible. Therefore, a generally applicable method for the preparation of cold ions that does not require direct laser cooling while efficiently suppressing quantum decoherence in ion systems is crucial for ion-based precision measurements and applications.

The Wineland group in the National Institute of Standards and Technology constructed the optical measurement systems for27Al+,which are based on sympathetic cooling using9Be+and24Mg+.[2,8,9]These “logic” ions also enable the internal quantum transitions of27Al+to be measured via their external degrees of freedom.This method was used to create frequency standards with an accuracy of 10-19,which were then used to validate special and general relativity.[2,8]Sympathetic cooling and quantum-logic measurements of an ion are performed by trapping a laser-cooled ion(LCI)and a sympathetically cooled ion(SCI)in a radio-frequency(RF)ion trap.These ion species will then be tightly coupled to each other through Coulomb interactions. Subsequently, a resonant energy transfer occurs between the SCI and the colder LCI, while heat is continuously removed from the system through laser Doppler cooling and sideband cooling. This continues until the two-ion system is cooled to thermal equilibrium by motional mode coupling(or even to the quantum mechanical ground state[9]in some cases). Once this state is achieved,the internal quantum state of the SCI and the external vibrational quantum state of the coupled SCI-LCI system can be manipulated using suitable pulsed lasers, thereby influencing the internal quantum state of the LCI. Quantum-logic operations on the SCI’s internal quantum state may then be performed by probing the internal quantum state of the LCI.Over the past 20 years,sympathetic cooling has been used in trapped ion systems to cool a variety of systems, both small (electrons) and large (biological molecules), to mK or μK levels.[10,11]It is now possible to control the motional modes and coupling characteristics of sympathetically cooled two-ion systems to hitherto unachievable levels of precision. This breakthrough enables precise quantum manipulations and measurements of charged ion systems with remarkable physical properties, which typically could not be directly laser-cooled. This allowed further precision in atomic clocks and in testing the fundamental theories of physics as well as in the construction of scalable quantum computers. Sympathetic cooling and quantum-logic operations based on ion trapping are now an important area of research for quantum logic clocks, quantum information processing, quantum computing, and cold chemistry.[12-17]Motional mode coupling between the SCI and LCI is an important factor for sympathetic cooling efficiency. It is also necessary for quantum-logic detection because it links the internal quantum states of the LCI and SCI.Therefore,the precise assessment and control of the motional mode coupling between the LCI and SCI are crucial for sympathetic ion cooling and high-precision ion spectroscopy.

In terms of structure and coupling mechanism, a linear two-ion pair in a linear Paul trap is the simplest quantumlogic system, and it has been widely implemented in scientific studies.[18]However, systematic studies on the motional mode coupling of two-ion systems are scarce, and the optimization of LCI-SCI interactions,mixed-ion systems,and potential fields remains poorly explored. Furthermore, the factors that influence the resonance modes and energy transfers of LCI-SCI systems have not been quantified. Owing to its physical properties,27Al+is one of the best candidate ions for atomic clocks and precision measurements,and it has been extensively studied.[2,8,9]However,direct laser cooling of27Al+is still very difficult,owing to the limitations of deep ultraviolet laser technology.[19]In this study, we will use the sympathetic cooling and quantum-logic operations of27Al+to study the motional mode coupling of LCI-SCI ion pairs.

2. Linear Paul trap for sympathetic cooling of ion pairs and its equivalent resonance model

The linear Paul trap and the corresponding coordinates used in our study are shown in Fig.1. The lengths of the trapping part(B)and the remaining parts(A,C)of each electrode are 2z0=5.90 mm and 2ze=24.00 mm, respectively. The diameter of each electrode rod isd=8.00 mm, and the minimum distances between the trap axis and all electrodes arer0=3.50 mm. The confinement of the ions in the radial plane is obtained by applying a pair of RF fields(±1/2Urfcos(Ωrft))with the same frequency and amplitude and a phase difference ofπto two pairs of diagonal electrode rods(A1,3, B1,3, C1,3,and A2,4,B2,4,C2,4). The confinement of the ions in the axial direction is obtained by applying direct current (DC) voltageUendto the ends of the electrodes (A and C). A detailed description of the linear Paul trap can be found in Refs.[20,21].After the two-ion system is sympathetically cooled to the crystalline state, the equilibrium distance between the two ions becomesz=(Qz20/(32Uendπε0))1/3,[22]whereQis the electron charge of each ion, andε0is the permittivity of free space. These ions exhibit three-dimensional (3D) resonant motions about their equilibrium positions, which are coupled to each other to an extent. If we do not consider high-order resonances,[23]the motional mode couplings of the two-ion system divide vibrational modes into the in-and out-of-phase eigenmodes. The external motional states may be expressed as the following Hamiltonian:

In these equations,ωiandωoare the angular eigenfrequencies of the in-and out-of-phase modes,respectively,andφiandφoare their phases.ziandzoare the modal amplitudes of the ion in- and out-of-phase vibrations, respectively. The mass ratio of the singly charged ion pair isμ=mLCI/mSCI.b1andb2are the components of the normalized eigenvector of the inphase mode,which satisfyb21+b22=1 in each dimension. The normalized eigenvector(b1,zandb2,z)of the axial vibrational modes of the ions depends directly on the mass ratiosμof the ion pair and satisfies

The normalized eigenvector(b1,randb2,r)of the radial vibrational modes depends on both the mass ratiosμof the ion pair and the radial-to-axial secular frequency ratio of the SCI,η=ωSCI-r/ωSCI-z,approximated by a harmonic pseudopotential model[25]and satisfies

The coupling intensities of the in-and out-of-phase vibrational modes of a LCI-SCI heteronuclear ion pair in specific dimensions are characterized by the absolute amplitude ratio of the heteronuclear ion pair in these modes[26]

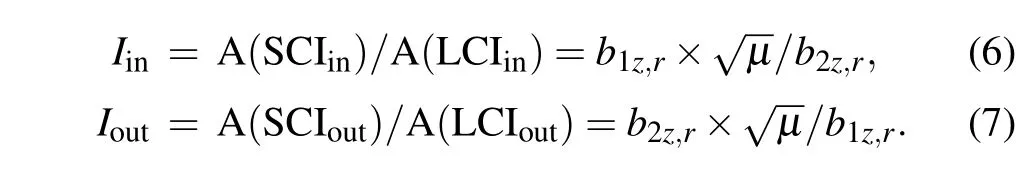
The closerIinandIoutare to 1,the stronger the coupling is.

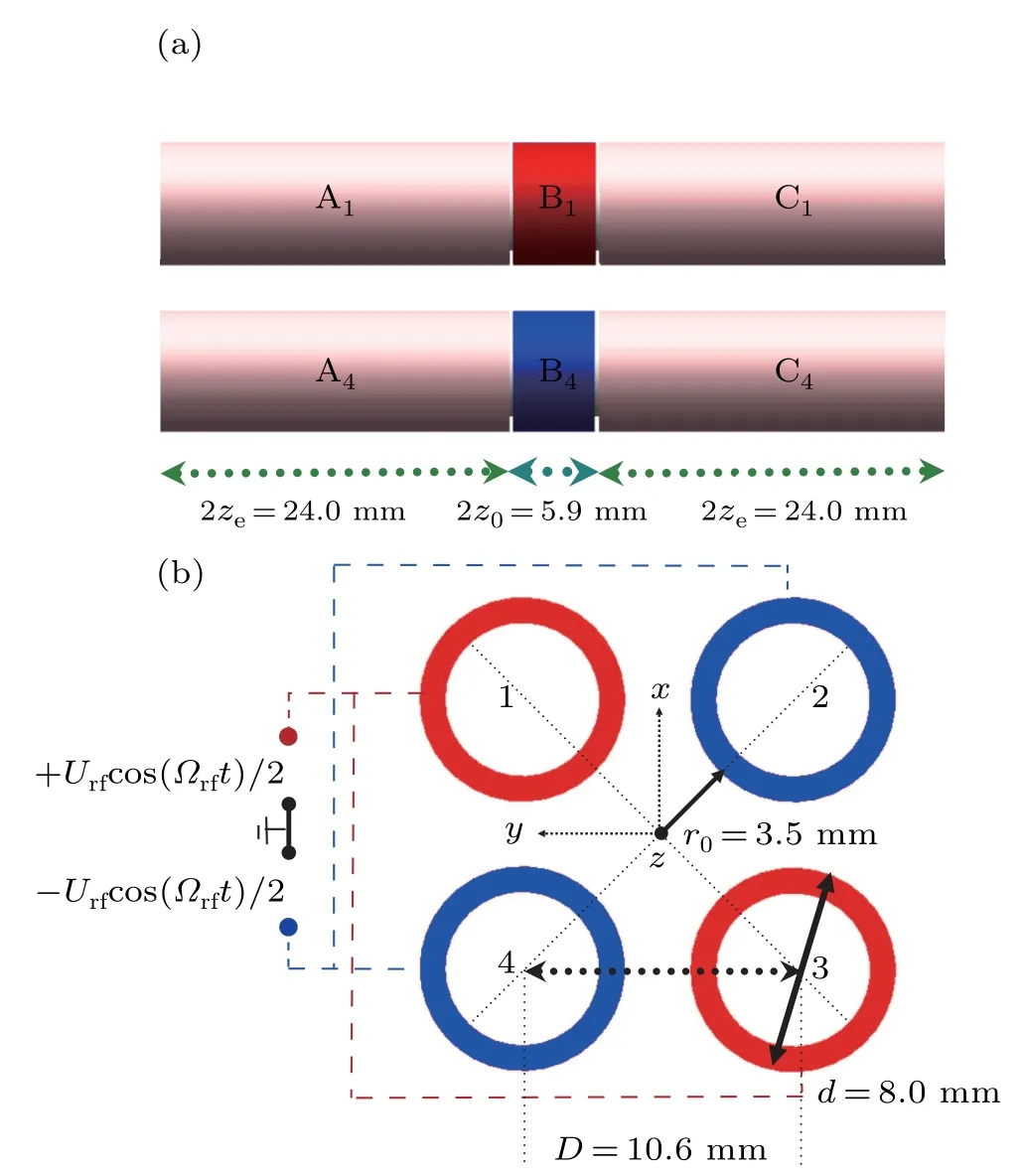
Fig.1. Schematic of the(a)linear Paul trap and(b)RF potential.

3. Secular spectra of sympathetically cooled ion pairs

The dynamics of RF-trapped ion systems can be approximated by using a harmonic pseudo potential model. Secular spectra are effective means for probing the dynamics of ion coupling, and they are also important for understanding and controlling sympathetic cooling and quantum-logic detection processes. We have used molecular dynamics simulations to study the dynamic coupling characteristics,spatial configuration,sympathetic cooling mechanism,and efficiency effect of ion pairs. The“leap frog”algorithm[27-29]is applied to solve the equation of motion of each particle. The kinematics information is monitored while the cloud moves under the influence of the RF trapping field,the Coulomb interaction forces,random collision force, and laser light interaction force. A detailed description of the numerical simulation methods can be found in Ref. [21]. The secular spectra of SCI pairs are obtained by applying a fast Fourier transform to the 3D coordinates of ions at different time.

3.1. Motional resonance spectrum of a single ion

The axial motions of a linearly trapped ion are determined by using the axial electrostatic potential. By minimizing the radial micromotions of the ion using the fluorescence modulation technique,[30]the radial (xandy) forces and secular motions of the ion system converge to a set point,and its motions are then jointly determined by the RF potential and axial electrostatic potential. Figure 2 shows the 3D secular spectra of singly trapped single40Ca+and27Al+ions under the same RF field (Ωrf=3.7148 MHz,Urf1=200 V,Uend=3.5 V),and the27Al+spectra were obtained by removing the40Ca+contribution to the40Ca+-27Al+pair through secular motional excitation or by controlling a radially symmetric electrostatic potential. Because the radial trapping strength of the trapping potential is higher than the axial trapping strength for a given ion,the radial secular frequency is higher than the axial secular frequency.

The axial and radial motional resonances of single40Ca+and27Al+ions are primarily basic modes. Their axial peaks areωAl-z= 137.315 kHz andωCa-z= 112.658 kHz, and their radial peaks areωAl-r= 268.254 kHz andωCa-r=174.301 kHz, respectively. In the harmonic pseudo potential model, the axial and radial secular frequencies of40Ca+and27Al+satisfy[24]

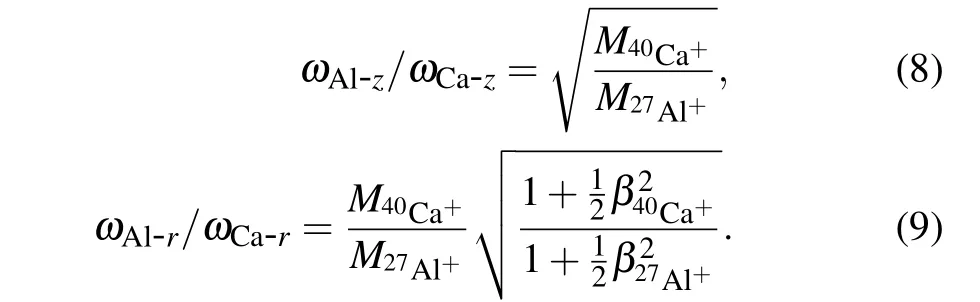
In these equations,β=ωz/ωris the ratio between the axial and radial equivalent binding strength of an ion.[24]The matching errors between the axial and radial resonance frequencies obtained from the simulations and their approximations from the equivalent pseudo potential were lower than 0.000168% and 0.509%, respectively (the accuracy of the latter was primarily limited by ignoring the high-order nonharmonic potential in the equivalent pseudo potential approximations). Thus,it is shown that the effect of high-order resonant modes on 3D resonance modes of single ions in a linear trap is negligible. Therefore, these modes are well approximated by the harmonic pseudo potential model.

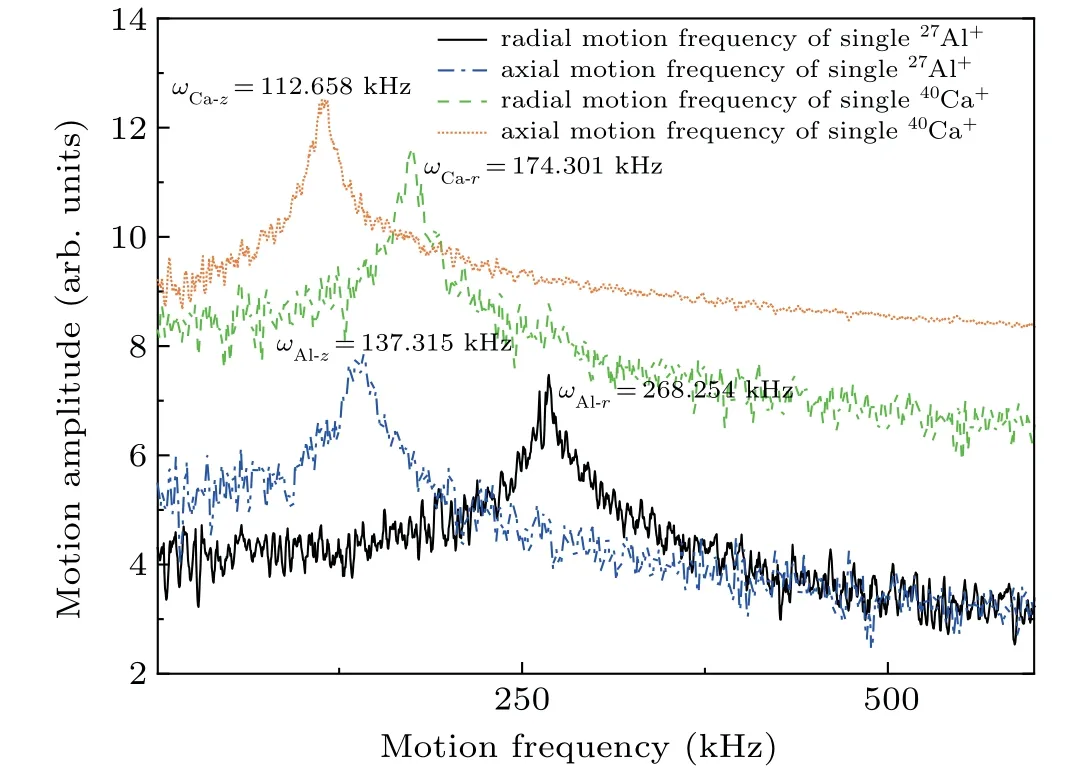
Fig.2.3D secular spectra of trapped single40Ca+and27Al+ions.The27Al+spectra were obtained by removing the 40Ca+ contribution to the 40Ca+-27Al+ pair through secular motional excitation or by controlling the radially symmetric electrostatic potential.

3.2. Motional mode coupling in the 40Ca+-27Al+pair

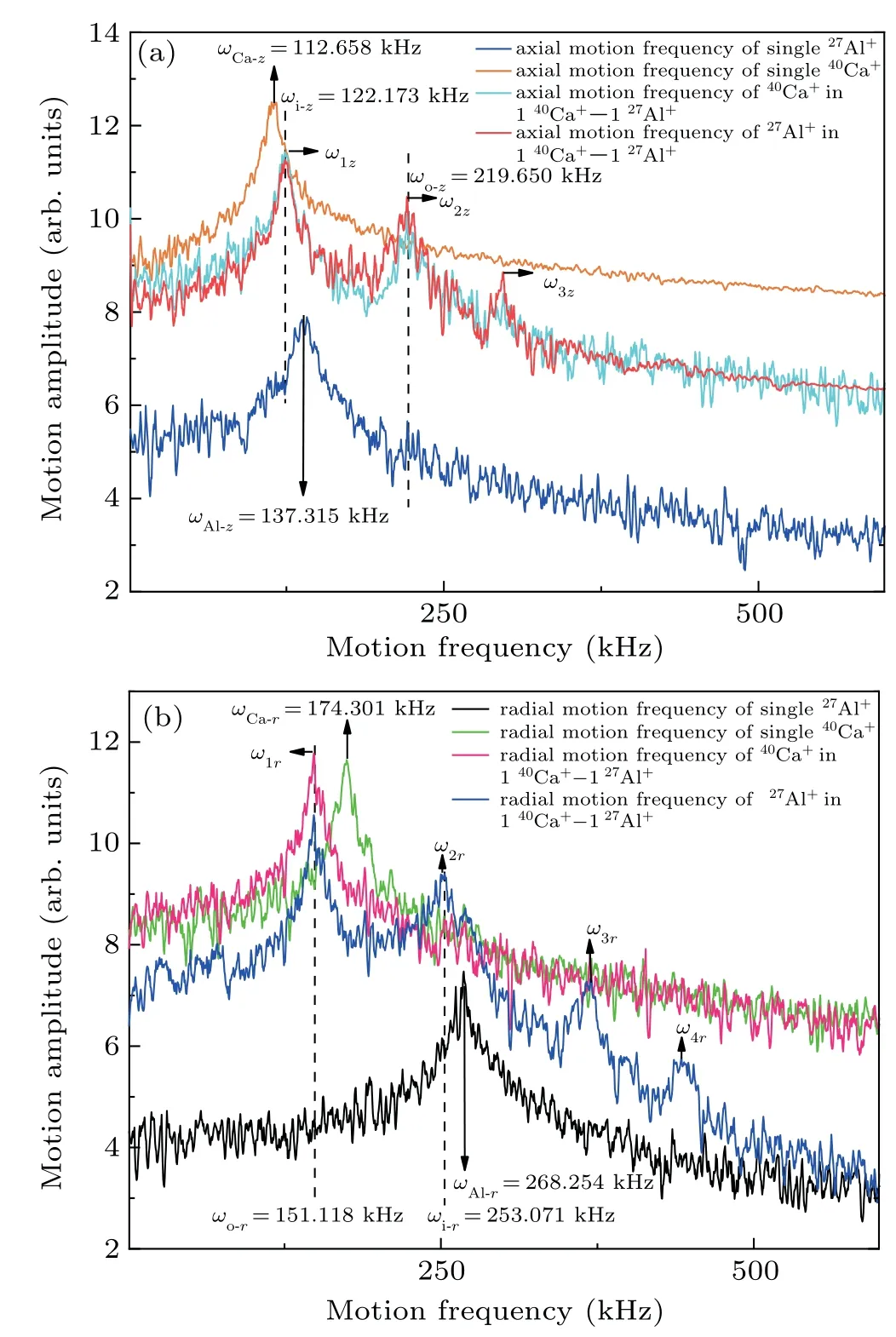
Fig.3. (a)Axial and(b)radial secular spectra of the 40Ca+-27Al+ two-ion crystal formed by the sympathetic cooling of a single27Al+ion using a single 40Ca+ ion.

Because the radial coupling modes of the40Ca+-27Al+pair are both fewer in number and weaker than their axial coupling modes,the efficiency of sympathetic cooling in this system is primarily determined by the axial resonance coupling.It may also be observed that the 3D secular spectra of the40Ca+-27Al+pair are generally in good agreement with the in- and out-of-phase modes predicted by the mode coupling theory for a pair of ions in equilibrium. The matching errors were primarily caused by the inability of mode coupling theory to account for higher-order coupling.

4. Effect of mass mismatches on the motional mode coupling of two ions and selection of an optimal LCI

Differences in the ion mass in a singly charged two-ion system will inevitably lead to differences in its effective potential and RF heating rates.[30]Quantitative studies on the effect of mass ratio variations on the motional mode coupling in two-ion systems are crucial to construct optimal ion systems for sympathetic cooling and high-fidelity quantum-logic operations. At present, laser cooling can only be used on ions with simple energy structures, such as9Be+,24Mg+,40Ca+,87Sr+,113Cd+,137Ba+,and171Yb+. Other ion systems either lack a closed cycling transition or have cycling transitions that cannot be pumped by existing lasers. Once the target SCI is identified,the selection of an optimal LCI is an important factor that affects the efficiency of sympathetic cooling and the fidelity of precision measurements.

4.1. Effect of mass mismatches on the motional mode coupling resonance frequencies

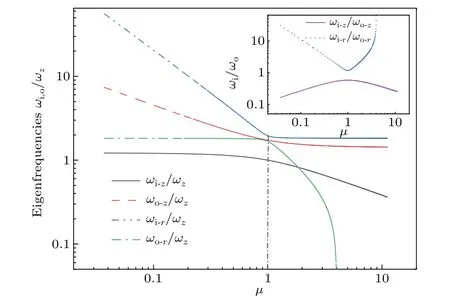
Fig.4. Relationships between the resonant-mode frequencies of an LCI-SCI pair and their mass ratio μ.

4.2. Effect of mass mismatches on the motional mode coupling vibrational amplitudes

In an ion pair with resonating normal modes, the relative mode amplitudes significantly affect the mode coupling strength and the sympathetic cooling rates. Figure 5 illustrates the amplitude ratios of the in- and out-of-phase modes of an LCI-SCI pair in each dimension,which were simulated by using the mode coupling theory for a pair of ions in equilibrium(the radial stability parameter of SCI isqSCI=0.215,and the pseudo potential well depth of SCI isDr,SCI=0.136 eV).[25]The strength of the external-state coupling in any mode increases as the ion mode amplitudes become more similar,which effectively increases the rates of sympathetic cooling.It is possible to maximize the sympathetic cooling efficiency by selecting a suitable LCI.

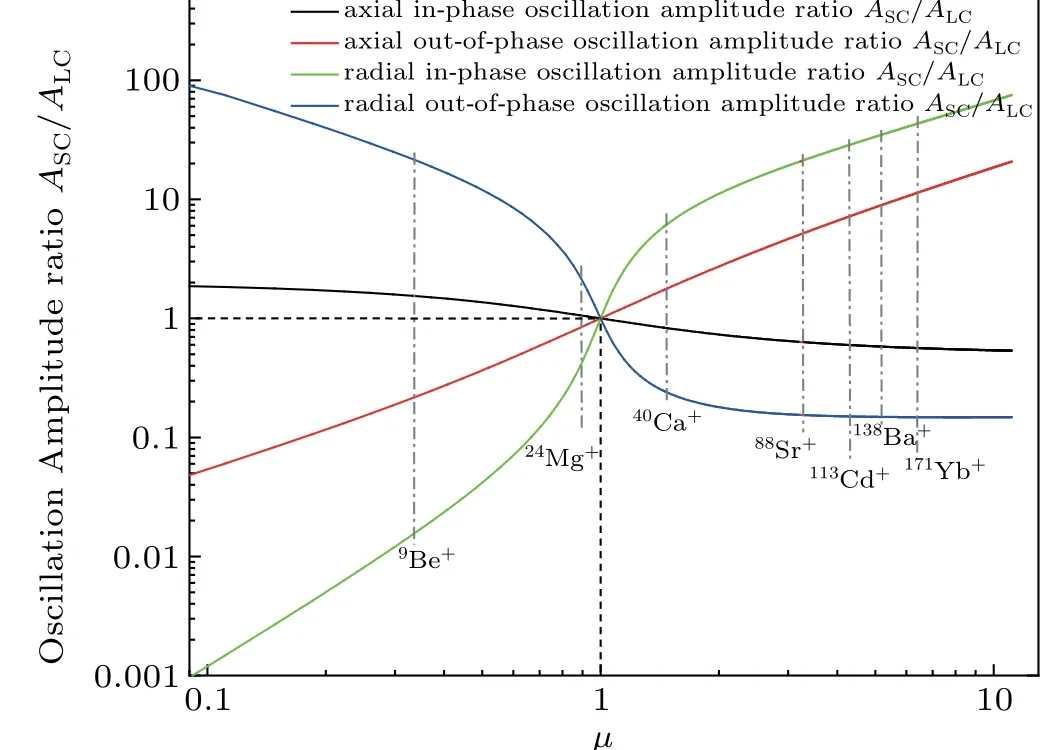
Fig. 5. Relationships between the relative resonance amplitudes of the inphase/out-of-phase modes of an LCI-SCI pair in each dimension and their mass ratio μ.

In the 0.1＜μ ＜10 interval, the difference between the axial (in- and out-of-phase) modes of the ion pair are significantly smaller than that between the radial modes, which indicates that the sympathetic coupling strength of the former is significantly higher than that of the latter.

The axial Coulomb interactions of an ion pair are dominated by the couplings of the in-phase mode,which is lower in frequency than the out-of-phase mode. In the in-phase mode,the vibrational amplitude of the heavier ion is slightly larger than that of the lighter ion. Therefore,the amplitude of the inphase mode is dominated by the SCI or LCI ifμ ＜1 orμ ＞1,respectively. Because the amplitude of the lighter ion is larger than that of the heavier ion in the out-of-phase mode,the amplitude of this mode is dominated by the LCI or SCI whenμ ＜1 orμ ＞1,respectively. Therefore,during axial sympathetic interactions between an ion pair, the lower frequency in-phase mode of the heavier ion and the higher frequency out-of-phase mode of the lighter ion have relatively large vibrational amplitudes. The selection of an LCI with a slightly higher mass than that of the SCI is beneficial for the suppression of the amplitude of the LCI’s axial in-phase mode through laser cooling,and it also indirectly tunes the amplitude of the SCI’s axial in-phase mode. This effectively suppresses the vibrational amplitude of the dominant axial in-phase mode of the ion pair, thereby increasing the overall sympathetic cooling efficiency of the ion pair.

In the radial sympathetic interactions of the ion pair, the coupling of the lower frequency out-of-phase mode is slightly stronger than that of the higher frequency in-phase mode. In the out-of-phase mode, the amplitude of the heavier ion is larger than that of the lighter ion,while the reverse is true for the in-phase mode.

As a whole, the four coupling relationships of the ion pair exhibit the following behaviors: the axial in-phase modes have the strongest coupling,followed by the axial out-of-phase modes, radial out-of-phase modes, and lastly, the radial inphase modes. The vibrational amplitudes of the heavier and lighter ions always dominate the lower and higher frequency vibrational modes,respectively.Reducing the mass mismatching in the ion pair suppresses inter-ion amplitude differences(in all vibrational modes and dimensions), improves vibrational mode coupling, and increases the sympathetic cooling rates. Conversely, excessively large mass mismatching can make simultaneous stabilization and the trapping of two different ions in a single RF field impossible, and this will also exacerbate the heating effect owing to ion micromotions.If the heating effect approaches or exceeds the (significantly worsened)sympathetic cooling effect,the sympathetic cooling efficiency of the ion pair will decrease rapidly while the equilibrium temperature rises steeply. Therefore,simultaneous trapping and sympathetic cooling of the ion pair may become impossible. If the pseudo potential well depth is maintained at reasonable values,an effective method that can be used to suppress RF heating is to reduce the radial stability parameterqof the two-ion system.[31]Because the ion pair is near the RF potential null of a linear trap,the RF heating effect for a given value ofqis significantly lower than that of a 3D ion system.Therefore, the range of mass-to-charge ratio differences used for sympathetic cooling in a two-ion system is significantly larger than that used in a 3D ion system.

4.3. Optimal LCI and its coupling frequency spectra

After the SCI is determined, an optimal LCI is selected to maximize coupling and sympathetic cooling rates for the LCI-SCI pair. This ensures the fidelity of quantum-logic operations and maximizes measurement precision.In the following section,we explore the differences between9Be+,24Mg+,40Ca+,87Sr+,113Cd+,137Ba+, and171Yb+in terms of their sympathetic interactions with27Al+using secular spectra,and we then select the optimal LCI.

The Doppler cooling linewidth and cooling energy level structure of an LCI determine its Doppler cooling limit temperature,thereby affecting the sympathetic cooling efficiency between the SCI and LCI. The Doppler cooling limit temperatures of the above mentioned seven LCIs are as follows:Tmin(9Be+) = 0.43 mK,[32]Tmin(24Mg+) = 1.005 mK,[33]Tmin(40Ca+) = 0.504 mK,Tmin(87Sr+) = 0.463 mK,[34]Tmin(113Cd+) = 1.440 mK,Tmin(137Ba+) = 0.346 mK, andTmin(171Yb+) = 0.449 mK.[35]Overall, there is no difference between these Doppler cooling limit temperatures in terms of the order of magnitude, and they are all below 2 mK. In this study, by sufficiently considering the difference between the Doppler cooling limit temperatures of different LCIs and various heating effects, the equilibrium temperatures of all the LCIs are adjusted in a unified manner to the order of 5 mK (this temperature is higher than the Doppler cooling limit temperature of each ion and is within the common equilibrium temperature range that canbe realized in experiments), while focusing on the motional mode coupling effects on the sympathetic cooling efficiency.Following on from the basic conclusion,a targeted analysis is performed to examine the additional effects of the difference between the Doppler cooling limit temperatures of the main candidate ions on the conclusion.

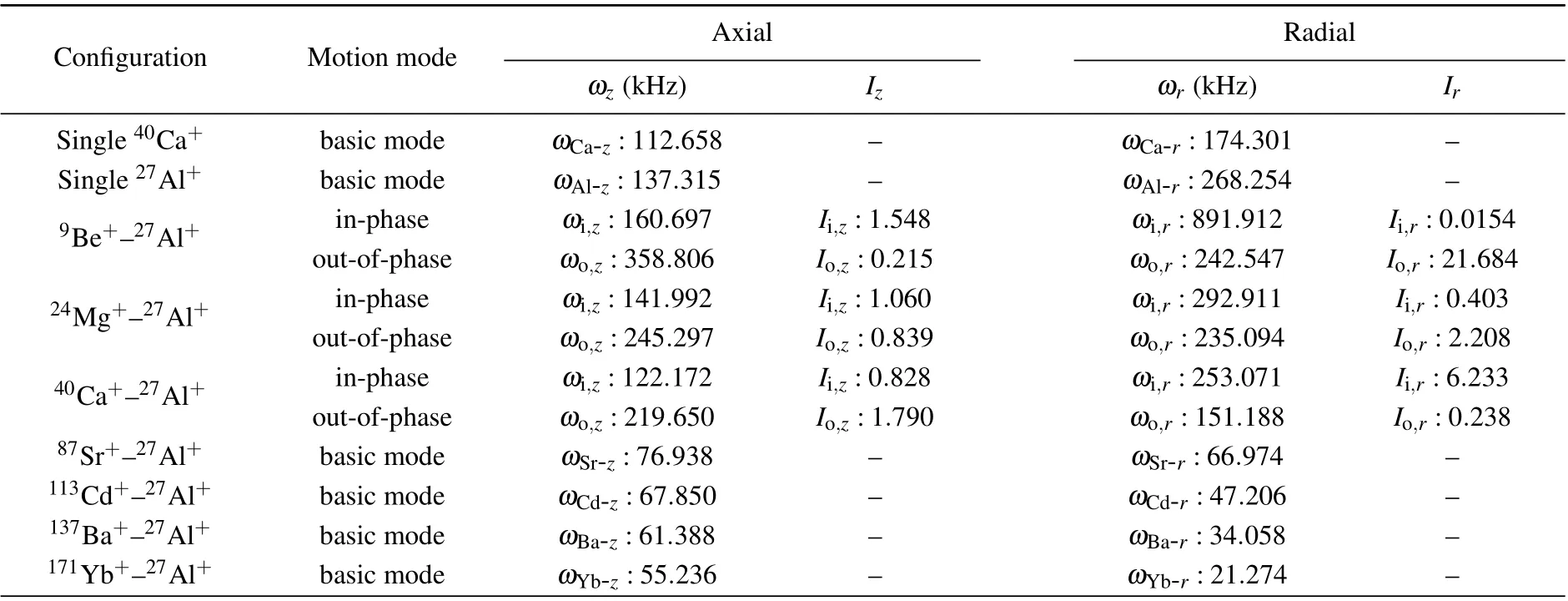
Table 1. Numerical calculated 3D motion mode spectra ωz,r and normalized mode coupling intensity Iz,r for trapped single ion and mixedspecies LCI-SCI pairs when 9Be+, 24Mg+, 40Ca+, 87Sr+, 113Cd+, 137Ba+,and 171Yb+ were used as the LCI for the sympathetic cooling of 27Al+ (the radial stability parameter of 27Al+ is qAl=0.215,the pseudo potential well depth of 27Al+ is Dr,Al=0.136 eV).

Fig.6.(a)Axial and(b)radial secular spectra that were observed when9Be+,24Mg+,40Ca+,87Sr+,113Cd+,137Ba+,and171Yb+were used as the LCI for the sympathetic cooling of 27Al+.

As mentioned previously, the sympathetic cooling rates of an LCI-SCI ion pair are primarily determined by the coupling of their axial vibrational modes, with secondary contributions from radial mode coupling. Figure 6 shows the axial(Fig.6(a))and radial(Fig.6(b))secular spectra of the LCI in seven different SCI-LCI pairs (9Be+,24Mg+,40Ca+,87Sr+,113Cd+,137Ba+, and171Yb+as the LCI, with27Al+as the SCI, under the RF field:Ωrf=3.7148 MHz,Urf1=200 V,Uend=3.5 V.The radial stability parameter of27Al+isqAl=0.215,and the pseudo potential well depth of27Al+isDr,Al=0.136 eV). Significant in- and out-of-phase modes may be observed in the axial secular spectra of9Be+,24Mg+, and40Ca+, which is indicative of strong coupling with27Al+. In the radial secular spectra,24Mg+shows significant in-and outof-phase modes, and40Ca+exhibits a significantly stronger out-of-phase mode than in-phase mode. Be+exhibits a significant in-phase mode; however, the intensity of its out-ofphase mode is negligible.87Sr+,113Cd+,137Ba+,and171Yb+only exhibit one significant vibrational peak in their axial and radial spectra, which closely matches their theoretical secular frequency. Shown in Fig. 6, the 3D motion mode main spectra peakωz,rand normalized mode coupling intensityIz,rfor trapped mixed-species LCI-SCI pairs are summarized and compared in Table 1.It may be assumed that24Mg+,40Ca,and9Be+formed tightly coupled ion systems with27Al+,whereas87Sr+,113Cd+,137Ba+, and171Yb+formed weakly coupled ion systems with large mass mismatches.

Figure 7 shows the (a) axial and (b) radial secular spectra of the(tightly coupled)24Mg+-27Al+,40Ca+-27Al+, and9Be+-27Al+ion pairs(under the RF field:Ωrf=3.7148 MHz,Urf1=200 V,Uend=3.5 V, the radial stability parameter of27Al+isqAl=0.215, and the pseudo potential well depth of27Al+isDr,Al=0.136 eV).These three ion pairs exhibited inand out-of-phase modes in all three dimensions.The matching errors between the resonance peaks of the ion pairs and their mode coupling theory-predicted in- and out-of-phase modes were generally less than 2%. In addition, the in- and out-ofphase modes of the ion pairs generally red shifted with increasing LCI mass.

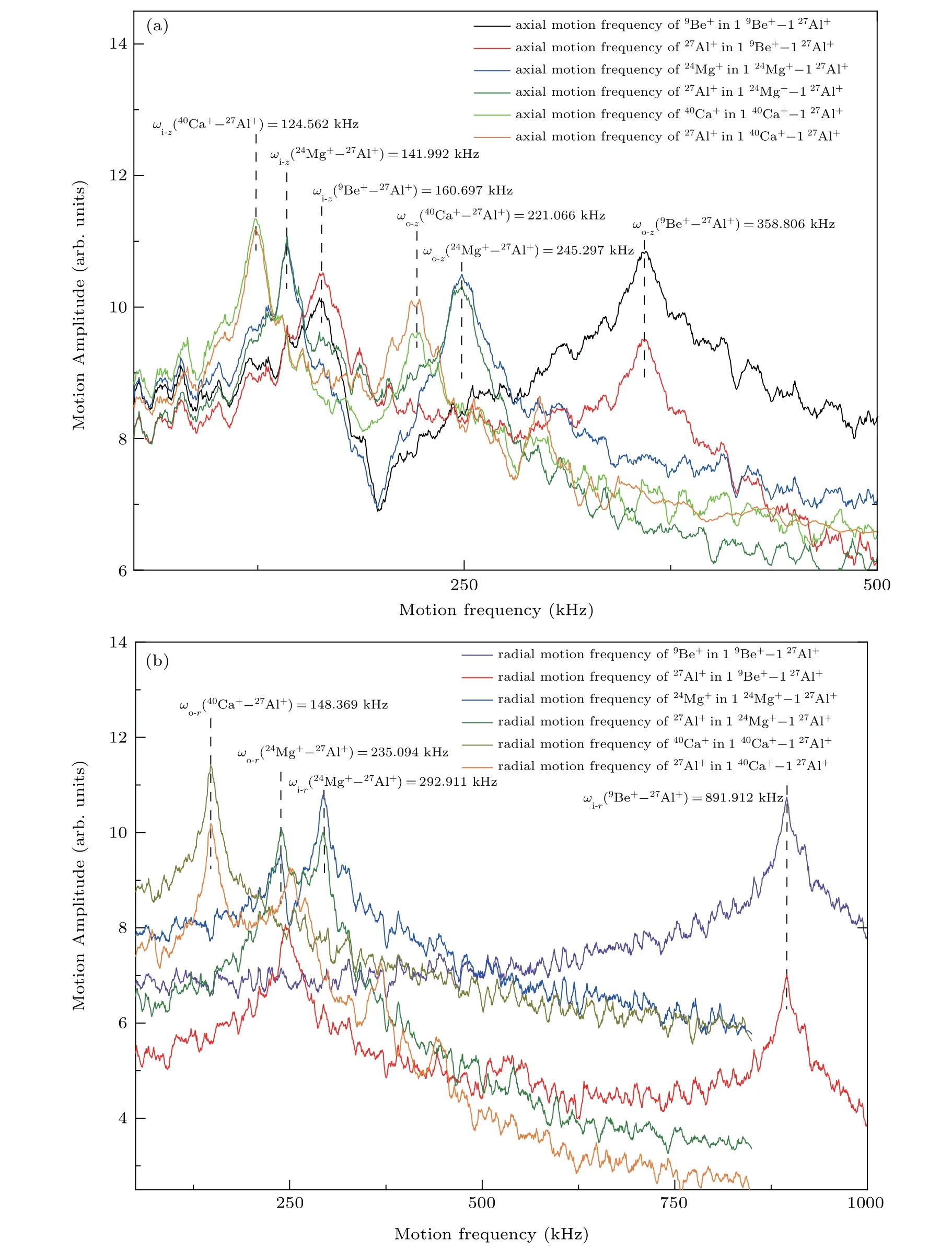
Fig.7. (a)Axial and(b)radial motional spectra of the 9Be+-27Al+, 24Mg+-27Al+,and 40Ca+-27Al+ pairs.

In the axial direction, the in-phase (out-of-phase)modes of the24Mg+and27Al+in the24Mg+-27Al+pair are relatively similar to each other in amplitude, which is indicative of strong coupling. The ions in the40Ca+-27Al+pair are strongly coupled through their in-phase vibrational modes;however, the out-of-phase mode of27Al+is slightly stronger than that of40Ca+,which is indicative of weaker coupling. In the9Be+-27Al+pair, the in-phase mode of27Al+is slightly stronger than that of9Be+, whereas its out-of-phase mode is significantly weaker, and the overall coupling of the9Be+-27Al+pair is considerably weaker than that of the40Ca+-27Al+pair. In the radial direction, the in- and out-of-phase modes of the ions in the24Mg+-27Al+pair are both strongly coupled. The40Ca+-27Al+pair is strongly coupled in the radial out-of-phase mode, but weakly coupled in the radial inphase mode. In the9Be+-27Al+pair, the in-phase mode of27Al+is significantly weaker than that of9Be+, which is indicative of weak coupling. The out-of-phase mode of27Al+is stronger than that of9Be+by several orders of magnitude,indicating that their coupling is negligible.

Based on the results above, it may be concluded that the24Mg+-27Al+pair has the strongest sympathetic interactions, in both the axial and radial directions. The40Ca+-27Al+pair exhibits the second strongest interactions, and the9Be+-27Al+pair has the weakest sympathetic interactions.However, the Doppler cooling limit temperature of40Ca+(Tmin(40Ca+) = 0.504 mK) is comparable to that of9Be+(Tmin(9Be+)=0.43 mK) but lower than approximately half of that of24Mg+(Tmin(24Mg+)=1.005 mK). Furthermore,laser cooling systems for40Ca+are more reliable than those for24Mg+and9Be+(both the 397 nm and 866 nm cooling lasers for40Ca+can be directly generated from an externalcavity semiconductor laser,whereas the 280 nm cooling laser for24Mg+needs to be indirectly generated by frequency multiplication and the 313 nm cooling laser for9Be+needs to be indirectly generated by frequency multiplication and combination).Therefore,the40Ca+-27Al+pair is probably the best ion pair for sympathetic cooling and logic operations and has particularly more notable comprehensive advantages in engineering applications such as the development of compact, transportable27Al+optical clocks with high environmental adaptabilities.

5. Conclusion

In this study, we have investigated the motional mode coupling of sympathetically cooled mixed-ion crystals by quantifying the 3D secular spectra of trapped ions. The 3D resonance peaks of the40Ca+-27Al+pair obtained by using this method were in good agreement with the in- and out-ofphase modes predicted by the mode coupling theory for a pair of ions in equilibrium. The sympathetic cooling efficiency of the40Ca+-27Al+pair is primarily determined by the coupling of the ion axial modes. The axial in-phase mode was the most strongly coupled mode,followed by the axial out-ofphase mode, radial out-of-phase mode, and lastly, the radial in-phase mode. The vibrational amplitudes of the heavier and lighter ions dominate the lower and higher frequency modes,respectively. Decreasing the mass mismatching in an ion pair improves their coupling in all dimensions,thereby improving the sympathetic cooling rates.87Sr+,113Cd+,137Ba+, and171Yb+formed weakly coupled, highly mismatched ion systems with27Al+, whereas24Mg+,40Ca+, and9Be+formed tightly coupled ion systems with27Al+. Compared with the24Mg+-27Al+pair and9Be+-27Al+pair, laser cooling systems for the40Ca+-27Al+pair are more reliable,and the latter has a minimum cooling temperature as low as 0.5 mK.Therefore,the40Ca+-27Al+pair is probably the best overall pairing for sympathetic cooling and logic operations and has particularly more notable comprehensive advantages in the development of highreliability, compact, transportable27Al+optical clocks. Highly charged ion (HCI) optical clocks and nuclear optical clocks are new interests in the fields of research in recent years. These ions exhibit better linewidths and environmental immunity compared to the outer-layer electron transition properties of conventional singly charged ions and are currently pinning great hopes on sympathetic cooling and quantum-logic measurements to achieve optical clock applications. The high-charge properties of HCIs often result in extremely low mass-to-charge ratios (e.g., Ar13+).9Be+is currently the best match for HCIs in terms of the sympathetic cooling efficiency. For the HCI-LCI pair, it is necessary to further focus on the effects of the strong Coulomb interactions between the ions caused by the high-charge properties on ion cooling. The amplitude of an HCI’s excess micromotion is positively correlated with its charge,Q, and they are much more sensitive to external perturbations than those of SCI systems. The trapping lifetime of HCIs may be greatly shortened by collision-induced charge transfer, which results in issues such as the creation of down-charged HCIs. Therefore, more stringent requirements are introduced for the level of vacuum and assembly accuracy of ion traps, the suppress the heating effects of random electronic thermal noise and micromotion,efficient ion trapping from high to low energy, and externalstate high-fidelity coupling over long distances. As a candidate ion for nuclear optical clocks,229Th3+garners the most attention.[36,37]Sr+may be a relatively suitable LCI for sympathetic cooling of229Th3+due to the following main reasons:Sr+and229Th3+have similar mass-to-charge ratios, which can facilitate motional mode coupling. The cooling lasers for Sr+are relatively mature (both the 422 nm and 1092 nm lasers can be generated directly from a semiconductor laser),and Sr+has a minimum Doppler cooling limit temperature as low as 0.463 mK. In addition, Sr+itself has a relatively good optical clock transition reference. As a result,229Th3+and Sr+can be evaluated by measurement comparisons in the same external field environment. The Sr+-229Th3+pair has notable advantages in measuring the time-varying characteristics of fundamental physical constants. The outcomes presented in this study will contribute to the development of highfidelity quantum-logic techniques based on the multiple resonance modes,efficient sympathetic cooling for highly charged ions,and the construction of more precise atomic clocks.