高位码垛机抓手张开机构的运动学分析

程相文，王 成，周 勇，殷海桐

(华北理工大学 机械工程学院，河北 唐山 063200)

0 引言

伴随着国家工业生产技术的快速发展，市场竞争也越来越激烈，在提高生产效率的同时尽可能地压缩产品的开发周期成为了各行各业共同追求的目标[1]。使用机器进行产品的搬运和码垛已经在众多工业生产领域得到了广泛地应用，极大地提高了工业生产效率，节省了大量的人力及财力，也在一定程度上降低了工作人员在作业期间遭遇事故的风险[2]。随着生产步伐的加快和生产规模的不断扩大，工业生产对码垛机的工作效率、负载能力、机构稳定性等性能提出了更高的要求，对码垛机的结构设计和可靠性也提出新的挑战。在此行业背景下，本文对负载50 kg、码垛的对象为袋装饲料的GW型自动码垛机抓手进行了运动学分析。

1 三维模型的建立

首先，运用Creo三维建模软件建立码垛机抓手张开机构的三维模型，如图1所示。

1-机架；2-平衡连接杆；3-拐臂Ⅱ；4-气缸；5-拐臂Ⅰ

抓手张开机构动作过程中，由张开气缸提供驱动力，驱动反转四连杆机构，实现抓手机构的张开与闭合。其中反转四杆机构由拐臂Ⅰ、拐臂Ⅱ、平衡连接杆和机架构成。

2 抓手张开机构运动学分析

采用解析法[3]对夹持机构对称性进行较为精确的数值分析。首先建立抓手张开机构运动简图，如图2所示，其中拐臂Ⅰ简化为三副构件EAC，拐臂Ⅱ简化为三副构件DBF，平衡连接杆简化为杆件EF，气缸套筒简化为CG，活塞杆简化为GD，AB为机架。经计算，机构的自由度为1，在气缸的驱动下，具有确定的运动轨迹。

图2 抓手张开机构运动分析简图

2.1 张开机构的角位移

对抓手张开机构进行运动分析，在机构简图的基础上建立坐标系，以A点为原点位置，以AB方向为x轴正方向，以竖直向下为y轴正方向，并标明各构件的位置角。

机构为一个六杆机构，通过观察可以看出机构存在两个封闭环，分别为：

封闭矢量环1：AE—EF—FB—BA；

封闭矢量环2：AC—CD—DB—BA。

因此，根据两封闭矢量环建立矢量方程组如下：

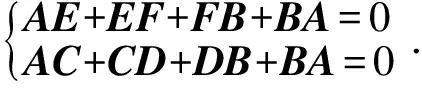
(1)

将方程组分别在x、y轴投影得到机构的运动学方程组：

(2)

其中:l0为杆AE的长度，mm；l1为杆AC的长度，mm；l2为杆BD的长度，mm；l3为杆EF的长度，mm；s4为CD的长度，mm；l5为杆BF的长度，mm；δ为∠DBF的值，(°)；θ0为杆AE与竖直方向夹角，(°)；θ1为杆AC与竖直方向夹角，(°)；θ2为杆BD与水平方向夹角，(°)；θ3为杆EF与水平方向夹角，(°)；θ4为气缸的水平偏斜角度，(°)；d为AB长度，mm。

式(2)是一个含三角函数的非线性超越方程组，在此采用牛顿辛普森迭代法[4, 5]求解。

将式(2)按牛顿辛普森法简化，并以矩阵形式表达如下：

(3)

至此，通过MATLAB编写程序，对式(3)进行求解，即可得到机构的角位移，可以绘制出相应的位移曲线。计算得到的抓手张开机构角位移线图如图3所示。

图3 抓手张开机构各杆件角位移

抓手张开机构的一个重要指标就是两拐臂的开度是否对称。因此为了分析抓手张开机构的对称性，将三副构件EAC与x轴的夹角∠CAB记为φ1；三副构件DBF与x轴的夹角∠DBA记为φ2，绘制出抓手张开过程中φ1、φ2的变化曲线，如图4所示。

图4 抓手张开过程中φ1和φ1变化曲线

从图4中可以看出，两拐臂与x轴的夹角并不完全一致，因此，两拐臂的同步性较差，需要进一步优化。

2.2 张开机构的角速度

为了计算张开机构各杆件的角速度，需要对位移方程组(2)进行求导，为了方便计算机编程计算，将速度方程组写为如下矩阵形式：

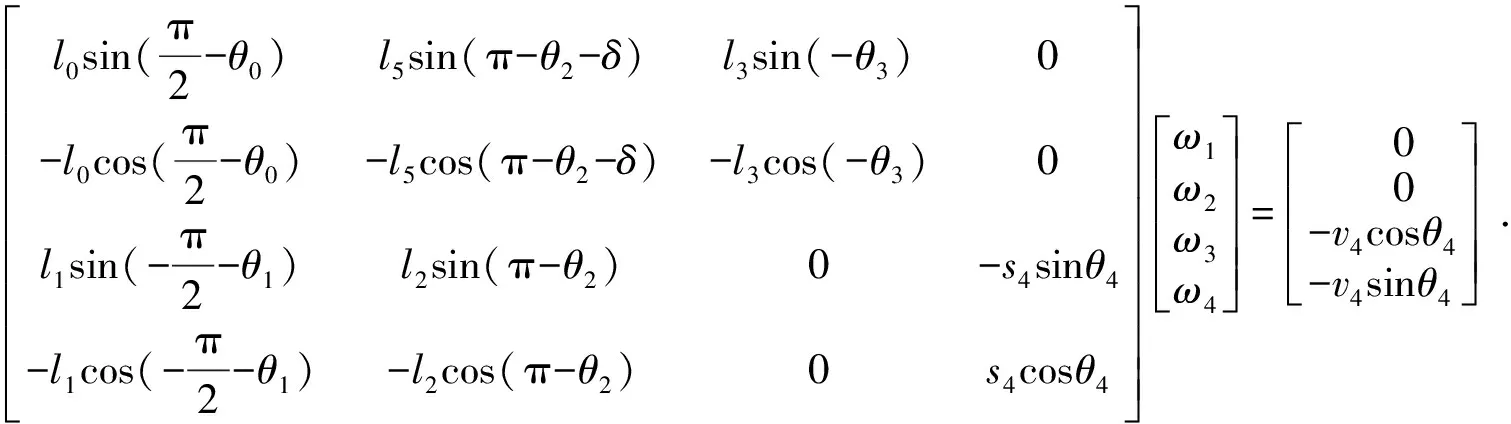
(4)

其中：ω1为三副构件EAC角速度；ω2为三副构件DBF角速度；ω3为杆EF角速度；ω4为气缸角速度；v4为气缸速度。

最后求得的各杆件角速度如图5所示。

从图5中可以看出，三副构件EAC和三副构件DBF的运行速度较为平稳且角速度反向，大小有小的偏差，符合实际情况，平衡连接杆的角速度最大，气缸由于是平动，角速度最小。

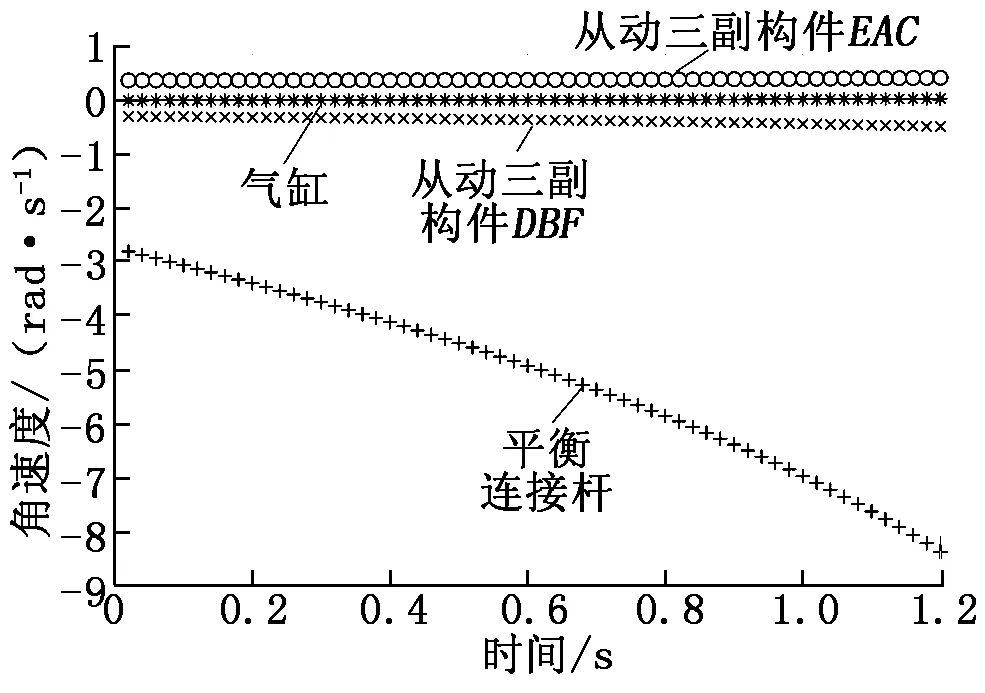
图5 抓手张开机构各杆件角速度

2.3 张开机构的角加速度

同理，求解角加速度需要对式(4)两端分别再求一阶导数，得到角加速度的矩阵方程如下：

(5)

其中：ε1为三副构件EAC角加速度；ε2为三副构件DBF角加速度；ε3为杆EF角加速度；ε4为气缸角加速度。

采用MATLAB求解矩阵方程(5)即可得到抓手张开机构各杆件的角加速度，如图6所示。

图6 抓手张开机构各杆件角加速度

3 结论

从抓手张开机构的运动学分析中可以看出张开机构在动作过程中存在不对称现象，这也与反转四杆机构本身的特性有关，因此，实际应用中要针对抓手张开机构的不对称现象进行杆长的尺寸优化，通过合理分配机构的杆长参数来达到机构对称性最优的目的。