智能优化算法在机械故障诊断领域的应用综述

洪晓翠， 段礼祥*， 杨晓光， 黄 谦

(1.中国石油大学(北京) 安全与海洋工程学院，北京 102249；2.中国石油集团工程技术研究院有限公司，北京 102206； 3.中海油田服务股份有限公司，河北 三河 065201)

随着科技的不断进步，石油石化、煤矿、航空等各个领域的机械设备逐渐呈现出智能化、整体化、精密化的特点，这意味着某一重要设备发生故障可能导致整个生产系统的崩溃。因此，开展机械设备的故障诊断对保障设备的安全运行、减少或避免灾难性事故的发生具有重要意义。目前，机械故障诊断主要包括基于特征工程的诊断方法和基于深度学习的智能诊断方法。基于特征工程的诊断方法采用“信号采集+特征提取+模式识别”的框架，即提取故障特征并进行特征优选，然后输入分类器进行分类。分类器多采用支持向量机(Support Vector Machine,SVM)等。利用优化算法对故障特征进行筛选以获取信息丰富、辨别能力强的特征，同时优化分类器参数以提高其性能对故障诊断具有重要意义。基于深度学习的智能诊断方法即构建深度神经网络自动提取故障特征并进行分类，网络的结构和参数直接影响故障诊断的效果。例如，对于卷积神经网络(Convolution Neural Network,CNN)，其性能主要取决于网络层数、卷积核尺寸、网络的连接权值和偏置等。换言之，寻找诊断模型的最优参数可极大地提高故障诊断的准确率。

智能优化算法是人们从生物进化的机理和一些物理现象中受到启发而提出的用于解决复杂优化问题的新方法，因其强大的优化性能而受到各领域学者的广泛关注，已在路径规划、图像识别、任务调度等多个领域得到了应用。20世纪后期，很多智能优化算法被提出，如遗传算法、蚁群算法等，经过数10年的发展，这些算法与其改进算法的研究和应用已比较成熟，这些算法被称为经典智能优化算法。随着人们对智能优化理论的深入研究与现代优化问题的日益复杂，近年来学者们提出了许多新型智能优化算法，如人工鱼群算法、人工蜂群算法等。传统优化算法如线性规划等，大多针对有清晰的结构信息、有唯一明确的全局最优点的结构化问题，不适于处理多极值、复杂的优化问题。相比于传统的优化算法，智能优化算法在求解过程中无需问题的特殊信息，对目标函数的要求更为宽松且具有较高的计算效率，是解决非线性、复杂优化问题的有力工具。

近年来，智能优化在机械故障诊断领域的应用也在逐渐增多，常用于故障特征的优选以及诊断模型结构和参数的优化等。主要讨论几种经典智能优化算法和新型智能优化算法在机械故障诊断领域的应用现状，总结算法的优缺点和改进算法，分析算法在故障诊断中的具体作用，并对未来的研究方向进行展望，为后续智能优化算法在机械故障诊断领域的进一步的应用提供参考。

1 机械故障诊断领域经典智能优化算法

1.1 遗传算法

1.1.1 算法原理及运算过程

遗传算法(Genetic Algorithm,GA)是由美国密歇根大学的Holland教授于1975年提出的一种智能优化算法，主要模拟了自然界的遗传机制和生物进化论。在GA中，用字符串类比染色体，通过选择、交叉和变异等遗传操作模拟生物的进化过程，用个体适应度值评价问题解的优劣程度。同时，根据适应度值确定种群进化方向，直至找到最优解。

GA的基本运算步骤如下。

① 初始化：主要包括种群规模、最大进化代数等参数；

② 个体评价：计算每个个体的适应度值；

③ 判断当前解是否满足要求或是否达到最大进化代数，若是，则终止计算，否则转向步骤④；

④ 选择运算：将选择算子作用于群体，并根据步骤②的评估结果，从当前解中选择满足要求的解，进行下一步基因操作；

⑤ 交叉运算：将交叉算子作用于群体；

⑥ 变异运算：将变异算子作用于群体，得到一组新的解，转向步骤②。

1.1.2 GA的改进算法

GA通用性强，搜索效率高、搜索过程灵活、全局寻优能力强。但是，GA对初始种群的选择具有依赖性，局部寻优能力差，且易早熟收敛。为此，很多学者提出了改进算法，主要集中在改进算法参数和结构、与其他算法相融合等方面。

Srinivas等[1]提出了自适应遗传算法，根据适应度值自适应调整算法的交叉概率和变异概率，使算法具有更强的搜索能力和收敛能力。Goldberg等[2]提出了遗传算法并行结构的思想，将遗传算法的并行模型分为主从式、细粒度和粗粒度三类。另外，相关研究将模拟退火算法、小生境技术与GA结合，提出模拟退火遗传算法[3]、小生境遗传算法[4]。

1.1.3 GA在机械故障诊断中的应用

通过对现有文献进行调研总结发现，GA在机械故障诊断中的应用主要体现在以下3个方面。

① 对故障特征进行优选。Guan等[5]提出一种多种群改进GA用于滚动轴承故障特征选择，可快速挖掘出有效的故障特征，实现了滚动轴承故障的精确诊断。Cerrada等[6]利用GA从齿轮振动信号中提取最佳的时域、频域和时频参数，建立了适用于齿轮多故障诊断的鲁棒系统。

② 优化人工神经网络结构、参数。Liu等[7]利用GA对反向传播神经网络(Back Propagation Neural Network,BPNN)的最优权值和阈值进行了优化，优化后的网络平均精度比标准网络提高了19%。刘浩然等[8]采用改进GA优化BPNN，并通过水泥回转窑故障诊断实验验证了方法的可行性。

③ 对其他诊断方法参数进行优化。例如，SVM常用于多故障分类，其性能主要取决于惩罚因子和核参数，采用智能优化算法寻找SVM的最优参数可有效提高诊断准确率，GA优化SVM参数并识别发动机磨损故障的流程如图1所示[9]。Zhu等[10]采用量子遗传算法优化SVM参数进行滚动轴承的故障诊断，相比于标准SVM，准确率提高了7.5%；王波等[11]采用量子遗传算法优化相关向量机核函数，实现了滚动轴承的有效诊断。

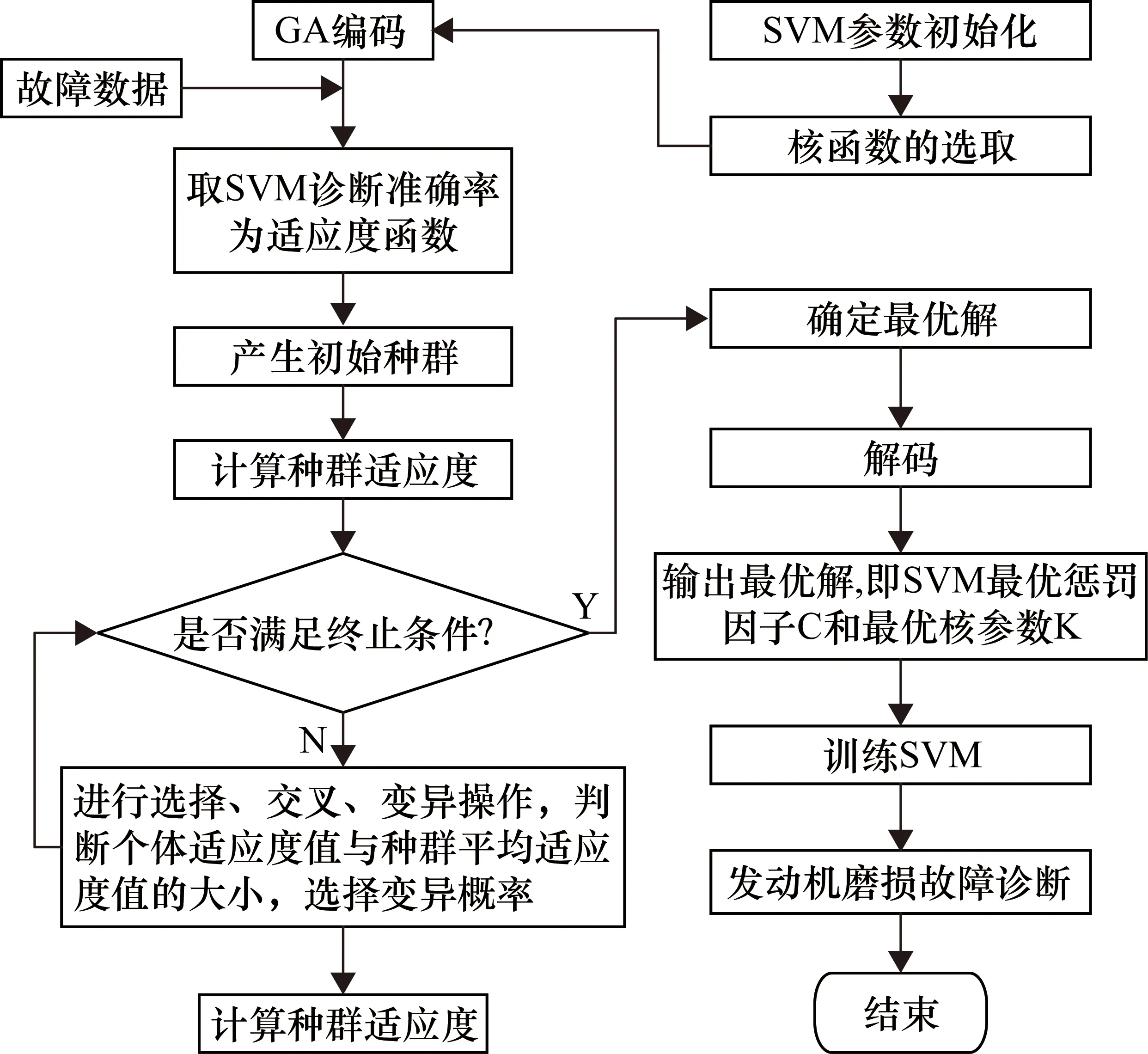
图1 GA优化SVM流程图

1.2 蚁群算法

1.2.1 算法原理及运算过程

蚁群算法(Ant Colony Optimization,ACO)是由Dorigo等[12]于1992年提出的，其灵感来源于蚂蚁的觅食行为。Dorigo等研究发现，蚂蚁在觅食过程中通过“信息素”实现信息的传递，并根据“信息素”的浓度确定到达食物源的最短路径。ACO通过构造人工蚂蚁模拟真实蚂蚁的行为，蚂蚁的行走路径即优化问题的解。

ACO的基本运算步骤如下。

① 初始化：主要包括蚁群规模、信息素浓度、蚂蚁初始路径等参数；

② 质量评估：计算每个蚂蚁所选路径对应的目标函数，评估路径的质量；

③ 路径选择：蚂蚁根据信息素浓度，利用概率选择独立构建自己的寻优路径；

④ 信息素更新：完成路径选择后，通过对路径上信息素的积累和挥发更新信息素；

⑤ 迭代终止：循环步骤②～步骤④，直至达到迭代终止条件。

1.2.2 ACO的改进算法

ACO的正反馈和分布式并行计算机制使得算法可靠性和全局寻优能力增强，同时具有鲁棒性强、参数少、设置简单、易与其他算法融合的优点。但是，在具体应用过程中，ACO还存在计算量大、搜索时间过长、易陷入局部最优等缺陷。针对上述问题，学者们主要从结构改进、参数选取与优化、与其他算法相融合等方面对算法进行改进[13]。

Duan等[14]提出了“三步”优化配置策略对ACO参数进行设置，有利于算法在各种优化问题中的应用和发展。Yi等[15]提出自适应机制和变异策略更新算法参数，增强了算法运算效率和局部搜索能力。Chen等[16]将ACO与GA融合，显著提高了算法的收敛能力。张毅等[17]在精英蚁群算法中引入了独狼算法用以改进算法搜索机制中蚁群的寻径能力。李春祥等[18]将ACO与粒子群算法相结合，充分发挥了ACO较好的全局搜索能力和粒子群算法的分级搜索机制。

1.2.3 ACO在机械故障诊断中的应用

作为经典智能优化算法之一，ACO在机械故障智能诊断领域得到了广泛的应用，主要用于人工神经网络、SVM等诊断方法的结构和参数优化以及多故障的聚类分析等。

① ACO优化诊断方法的结构和参数。在优化过程中，ACO常用于确定网络的最佳层数、寻找网络最优参数，如网络连接权值、偏置等。Ma等[19]利用ACO优化深度置信网络参数并建立故障诊断模型，实现了对轴承的在线健康状态监测，将诊断准确率提高了1.5%，测试时间由3412.5 s减少到1952.9 s。宋涛等[20]采用改进ACO解决最小二乘SVM模型中存在的核函数选择和参数确定问题，实现了柱塞泵的故障诊断。

② ACO用于聚类分析。蚁群聚类是一种结合ACO的智能聚类方法，可用于机械故障的识别和分类。祝勇仁等[21]采用蚁群聚类算法实现了离心式压缩机的故障诊断。王文瑾等[22]构建基于遗传变异的蚁群聚类诊断模型用于滚动轴承故障分类。

1.3 粒子群优化算法

1.3.1 算法原理及运算过程

粒子群优化算法(Particle Swarm Optimization,PSO)是由Kennedy等[23]于1995年提出，通过模拟鸟群觅食行为而发展起来的一种随机搜索算法。在PSO中，“粒子”表示问题的解。每个粒子根据速度函数确定飞行距离和方向，通过适应度值评价粒子位置的优劣，并不断更新粒子位置和速度，直至找到最优位置即问题的最优解。

PSO的基本运算步骤如下。

① 初始化：设置种群规模、权重、学习因子等参数，随机生成具有位置和速度信息的粒子作为初始种群；

② 个体评价：计算每个粒子的适应度值；

③ 更新个体最优位置：对于每个粒子，将其当前的适应度值与个体历史最优位置对应的适应度值作比较，如果当前位置更优，则将当前位置设为个体最优位置；

④ 更新全局最优位置：对于每个粒子，将其当前的适应度值与全局最优位置对应的适应度值作比较，如果当前位置适应度值更优，则将当前位置设为全局最优位置；

⑤ 更新每个粒子的位置和速度；

⑥ 迭代终止：循环步骤②～步骤⑤，直至达到迭代终止条件。

1.3.2 PSO的改进算法

PSO在迭代过程中只把最优粒子信息传递给其他粒子，故搜索速度快，该算法还具有概念简单、参数少、易于实现的优点。但是，PSO对参数选择敏感，参数选择不当会严重影响求解质量，且容易陷入局部最优，导致收敛精度降低。很多学者针对PSO的缺陷提出了改进算法，改进策略主要为算法参数优化、与其他算法融合等。

邵良杉等[24]在PSO中引入变异操作，并构造一种新的粒子选择方法控制违反约束条件的粒子数量，提高了算法寻找边界的能力。Santos等[25]利用基于梯度的信息和分集控制来优化PSO的多峰函数，有效避免了算法陷入局部最优。邢飞[26]在标准PSO的基础上引入惯性权重因子和GA中的遗传变异算子，提高了算法的运算效率和局部寻优能力。

1.3.3 PSO在机械故障诊断中的应用

PSO概念简单、参数少、易于实现，在机械故障诊断中的研究成果层出不穷，主要用于故障特征选择、人工神经网络与其他诊断方法结构和参数的优化等。

① PSO用于故障特征优选。Tyagi等[27]采用PSO对滚动轴承振动信号进行最优包络窗的选取，显著提高了诊断性能。綦方中等[28]采用量子PSO对转子故障特征集进行二次优选获取故障模式辨识度高的低维故障数据集，显著提高了故障分类的准确率。

② PSO用于诊断方法结构和参数的优化。李涛等[29]使用PSO对CNN的7个关键参数进行优选，并构建深度学习模型，实现了对转子系统的精确诊断。Gan等[30]利用PSO优化SVM参数并与AdaBoost结合用于轴承的故障诊断，取得了98%的诊断准确率。量子PSO优化BPNN权值、阈值并实现电机故障诊断的流程如图2所示[31]。

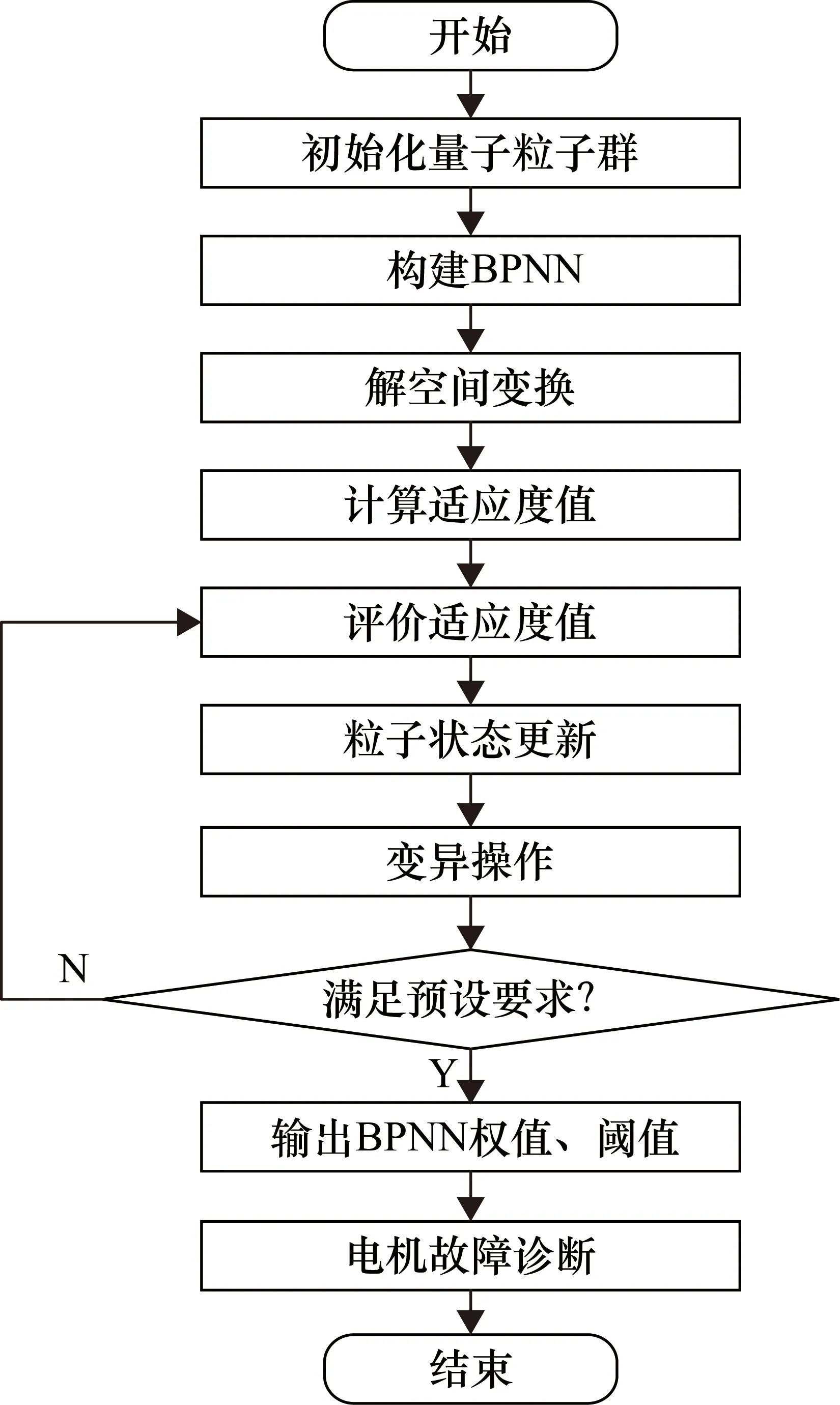
图2 量子PSO优化BPNN流程图

1.4 三种经典智能优化算法的作用及优缺点对比

在机械故障诊断领域的应用过程中，以上三种智能优化算法都有各自的具体作用和优缺点，如表1所示。从表1和上述内容可以看出，三种经典智能优化算法在应用、改进、多算法融合等方面的研究已比较成熟且成果充足。

表1 三种经典智能优化算法的对比

2 机械故障诊断领域新型智能优化算法

2.1 人工鱼群算法

2.1.1 算法原理及运算过程

人工鱼群算法(Artificial Fish Swarms Algorithm,AFSA)是中国学者李晓磊[32]于2003年提出的一种模拟鱼群行为的新型智能优化算法。AFSA通过构造人工鱼模拟真实鱼的觅食行为、聚群行为、追尾行为和随机行为，并根据所要解决的问题性质，对人工鱼当前所处的环境进行评价，从而选择一种行为，实现对优化问题的求解。

AFSA的基本运算步骤如下。

① 初始化：主要包括鱼群规模、人工鱼初始位置、人工鱼视野、步长、最大尝试次数、拥挤因子等参数；

② 个体评价：计算人工鱼适应度值，并记录最优人工鱼状态；

③ 行为选择：对人工鱼当前所处的环境进行评价，选择其要执行的行为；

④ 位置更新：执行人工鱼选择的行为，更新人工鱼位置信息；

⑤ 更新全局最优人工鱼状态：评价所有个体，若某人工鱼状态优于历史最优人工鱼状态，则将其值设置为全局最优值；

⑥ 迭代终止：循环步骤②～步骤⑤，直至达到迭代终止条件。

2.1.2 AFSA的改进算法

AFSA引入了动物自治体的概念，具有一定的自适应性，同时具有收敛速度快、全局寻优能力强等优点。但是，AFSA搜索后期效率低、盲目性大，相关学者对此进行了改进，主要为改进参数更新策略、与其他智能算法相融合等。

马梓元等[33]提出了一种人工鱼自适应视野模型，并对鱼群的进化策略在无性繁殖方式的基础上进行了改进，提高了算法的收敛速度和求解精度。曹法如等[34]提出动态调整视野和步长的策略来平衡算法局部搜索和全局搜索，有效地避免了算法陷入局部最优。Ma等[35]将GA中的交叉、变异算子引入到AFSA中调整种群进化策略和方向，提高了算法的寻优能力。喻曹丰等[36]将PSO快速局部搜索性与AFSA全局收敛性相结合，提出了一种高精度的混合优化参数辨识算法。

2.1.3 AFSA在机械故障诊断中的应用

AFSA一经提出便受到了各领域学者的关注，在机械故障诊断中的应用也在逐渐增多，主要用于人工神经网络和其他诊断方法参数的优化。

张宁等[37]利用改进的AFSA优化BPNN的权值和阈值，加快了网络的收敛速度，提高了轴承的诊断精度。Wang等[38]采用AFSA对深度自动编码器的关键参数进行优化，实现了齿轮箱和电力机车滚动轴承的故障诊断。史一明等[39]将PSO和AFSA相结合优化支持向量回归机参数，提高了滚动轴承可靠度预测模型的泛化能力和预测精度。Zhu等[40]采用AFSA优化变分模态分解中的分解模式数用于处理滚动轴承的振动信号并开展了有效的故障诊断。AFSA优化SVM参数流程如图3所示[41]。

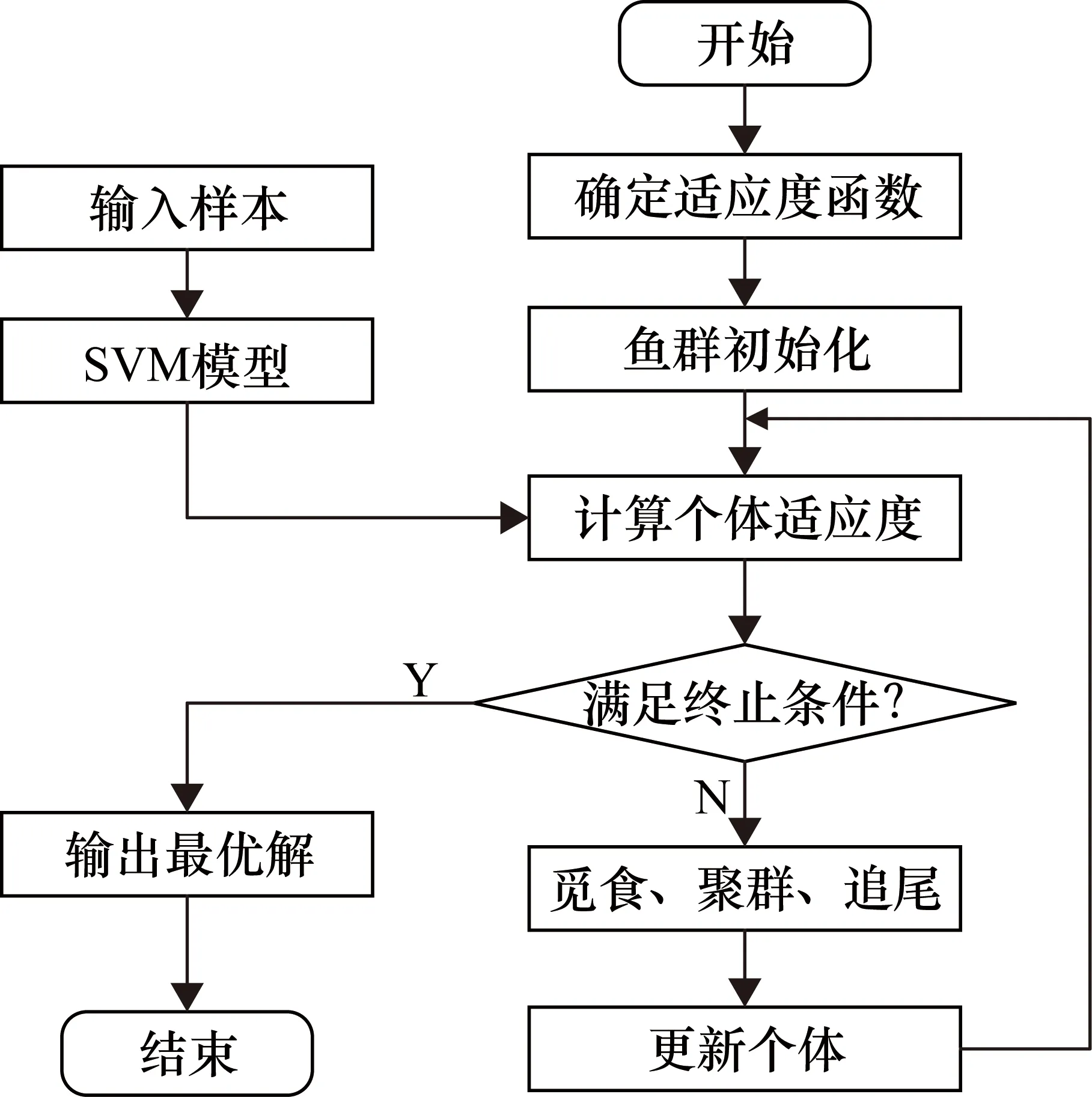
图3 AFSA优化SVM流程图

2.2 人工蜂群算法

2.2.1 算法原理及运算过程

人工蜂群算法(Artificial Bee Colony,ABC)是由土耳其学者Karaboga[42]于2005年提出的一种模仿蜜蜂行为的新型智能优化算法。在ABC中，蜜源的位置表示问题的解，用适应度值评估蜜源的质量，通过引领蜂、跟随蜂及侦察蜂的信息交流、相互协作寻找问题的最优解。

ABC的基本运算步骤如下。

① 初始化：主要包括蜂群总数、蜜源数量、最大迭代次数等参数，随机产生初始解并计算其适应度值；

② 产生新蜜源：为初始解分配引领蜂，使其在初始解邻域进行搜索产生新解，并计算其适应度值；

③ 质量评估：对比初始解和新解的适应度值，根据贪婪选择机制保留适应度值更高的解；

④ 跟随蜂阶段：计算蜜源被跟随的概率，跟随蜂根据概率选择对应的食物源，并采用与引领蜂同样的方式保留适应度值更高的蜜源；

⑤ 侦察蜂产生新蜜源：如果引领蜂在初始解附近搜索次数达到最高值但仍未发现更优解，则放弃初始解，同时引领蜂转化为侦察蜂并随机产生新蜜源，否则转至⑥；

⑥迭代终止：重复步骤②～步骤⑤，直至满足迭代终止条件。

2.2.2 ABC的改进算法

ABC全局寻优能力较强，且对初值设置无要求、适用性强，但存在后期搜索速度慢，易早熟收敛等缺陷。针对上述问题，学者们从参数优化、引入新策略、与其他算法相融合等方面对算法进行了改进。

简献忠等[43]在标准ABC基础上引入遗忘因子和邻域因子，在搜索的初期通过遗忘因子和邻域因子来使侦查蜂调整路径，从而能快速收敛到最优食物源所在区域，并使全局收敛性能在搜索后期有所提高。邱岳恒等[44]采用杂草入侵算法中的子代空间扩散机制和繁殖机制分别取代ABC中盲目性的进化方式和轮盘赌式的选择策略，解决了该算法可能出现收敛速度降低和陷入局部最优等问题。李平等[45]将差分进化算法融入ABC，增强了算法的全局优化能力。

2.2.3 ABC在机械故障诊断中的应用

ABC全局寻优能力较强，且对初值设置无要求、适用性强，在故障诊断领域也有一些研究成果，主要用于对人工神经网络和其他诊断方法参数的优化。

贾亦敏等[46]采用精英混沌人工蜂群算法对小波神经网络的输入和输出层权值、小波元的伸缩和平移系数进行优化，有效地开展了变压器故障诊断。Zhang等[47]利用ABC优化SVM参数对变压器开展故障诊断，优化后的故障诊断准确率提高了近19%；刘霞等[48]将混沌机制引入ABC，提出混沌人工蜂群算法用于优化SVM核函数和惩罚因子，并在齿轮故障诊断实验中取得了99.4%的准确率。

2.3 萤火虫算法

2.3.1 算法原理及运算过程

目前，萤火虫算法有两个版本，分别是印度学者Krishnanand等[49]于2009年提出的萤火虫群优化算法(Glowworm Swarm Optimization,GSO)和剑桥大学的Yang等[50]于2013年提出的萤火虫算法(Firefly Algorithm,FA)。目前，在故障诊断领域应用较多的是FA，故主要对FA进行概述。

FA是模拟自然界萤火虫的发光特性及相互吸引行为而提出的一种新型智能优化算法。在FA中，用目标函数表示萤火虫亮度，亮度越高则吸引能力越强，亮度较低的萤火虫会被亮度较高的萤火虫吸引。

FA的基本运算步骤如下。

① 初始化：主要包括种群规模、萤火虫位置、步长、吸引度等参数；

② 个体评价：计算各萤火虫的适应度值，得出每个个体的亮度；

③ 更新萤火虫位置：根据萤火虫亮度更新萤火虫位置，最亮的萤火虫不受吸引，进行随机移动；

④ 更新萤火虫亮度：根据更新后的位置计算萤火虫适应度值，更新萤火虫亮度；

⑤ 重复步骤②～步骤④，直至达到迭代终止条件。

2.3.2 FA的改进算法

FA由于概念简单、容易实现的特点而受到广泛关注，但也存在易陷入局部极值的缺点，有学者对此进行了改进，主要集中在参数改进、与其他算法相融合两方面。参数方面主要是对步长、位置更新策略等进行改进。

田梦楚等[51]结合粒子滤波的运行机制，设计了新的萤火虫位置更新公式和荧光亮度计算公式，提高了算法的寻优能力。莫愿斌等[52]利用单纯形法局部搜索速度快和FA全局寻优能力强的特点，提出一种基于单纯形法的改进型FA，有效地避免了算法陷入局部最优，提高了搜索精度。Zhang等[53]将量子理论和变异运算引入FA，每个量子萤火虫都可以表示解空间的两个位置，通过量子门计算实现位置更新，并通过变异操作跳出局部极值，有效地提高了算法的全局搜索能力和所求解的精度。张晗等[54]设计了一种融合多种群GA与FA的多种群萤火虫算法，提高了算法的寻优能力。

2.3.3 FA在机械故障诊断中的应用

作为一种新型智能优化算法，FA在机械故障诊断领域也有一定的研究成果，主要用于对人工神经网络结构、参数的优化。

李巍华等[55]提出一种双层FA并用其优化BPNN参数，提高了轴承故障的识别率。卓宏明等[56]利用FA优化BPNN的权值和阈值并进行柴油机故障诊断，将诊断准确率提高了5.1%。王奉涛等[57]提出了混沌萤火虫算法，并用其优化深度神经网络中的待定参数，实现了轴承故障的有效识别。

2.4 三种新型智能优化算法的作用及优缺点对比

三种新型智能优化算法在机械故障诊断领域的应用过程中都有各自的具体作用和优缺点，对此进行总结，如表2所示。

表2 三种新型智能优化算法的对比

从表2和上述内容可看出，三种新型智能优化算法在故障诊断领域的应用相对较少且存在很多不足，如AFSA、ABC在寻优过程中后期搜索的效率低，FA易陷入局部最优等，且在故障诊断领域如离心泵的故障诊断，往复压缩机的气阀、十字头等关键部件故障诊断方面的研究成果相对较少，还有很大的发展潜力，值得进一步探索研究。

3 结束语

通过论述、分析智能优化算法在机械故障诊断中的应用现状和不足，得出的结论与对未来研究趋势的展望如下。

① 经典智能优化算法的研究及应用已比较成熟。

就目前而言，GA、PSO等经典智能优化算法及其改进算法在机械故障诊断中得到了广泛的应用，研究已比较成熟且成果充足。

② 现有新型智能优化算法的性能仍需改进。由于提出时间有限，各领域尤其是机械故障诊断领域对现有新型智能优化算法的研究相对较少，且各算法在应用过程中仍存在不足，学者们可从改进算法参数设置及更新策略、融合两种或多种优化算法等方面进一步提升算法性能。

③ 人工智能技术的不断发展将刺激产生更多新算法。社会在不断发展，各个领域如图像识别、路径规划等将出现更多的优化问题，且均呈现出复杂、非线性、大规模的特点，传统优化算法由于自身的局限性难以处理现代优化问题，智能优化算法由于收敛速度快、精度高的优越特性而受到青睐。同时，人工智能技术的不断发展以及计算机软硬件设备的不断完善将更加促进专家学者对智能优化理论的研究，从而刺激产生性能更佳的智能优化算法。