基于Anusplin模型的衡水市2018年降水量空间精细化研究
2021-07-30于晓彤
于晓彤
(河北省衡水水文勘测研究中心,河北 衡水 053000)
1 概 述
降水资源是陆表生态环境发展的关键要素之一,精细化的降水资源空间分布式信息是实现水资源精确管理与水生态文明建设的数据支撑[1]。鉴于区域环境条件、经济成本等因素,我国国家级气象站(2404个)的分布密度仅为2.53个/104km2,而在局部高原山地荒漠地区的气象站点分布更加稀疏,这难以满足对降水数据精细化的需求[2-3]。随着遥感卫星技术的发展,获取广域地区实时降水量成为可能。学者们基于TRMM、GPM等卫星反演的降水产品开展了山地、高原、盆地等不同地形区的降尺度研究,实现粗糙级分辨率的降水信息呈现精细化,并且确保其精度[4-6]。鉴于此,本文拟以经典的Anusplin方法为基础,考虑降水分布的地带性规律,实现衡水市降水量降尺度研究,以期为区域水资源管理提供技术支撑。
1.1 研究区概况
衡水(E115°10′-E116°34′、N37°03′-N38°23′)位于华北黄淮海平原腹地、黄河下游以北、河北省中南部,行政区面积达2.35 km2。区域地处我国中纬度温带暖温带地区,气候受东南季风与高纬度冷高压影响而形成温带季风气候,具有水热同期、季候差异显著、季节温差大的特点,区域多年平均温度12.6℃,多年平均降雨量509.7 mm,其中降水资源多集中于每年的5-8月份,约占全年降水量的50%~60%。衡水地形平坦,有洼地、岗地等地貌,高程介于0~35 m之间,地形坡面小于1/3 000。境内属海河水系,发育有滏阳河、滹沱河、潴龙河等较大河流,流速平缓、流量较小,地表水资源量为0.13×108m3,人均水资源占有量缺乏。见图1。
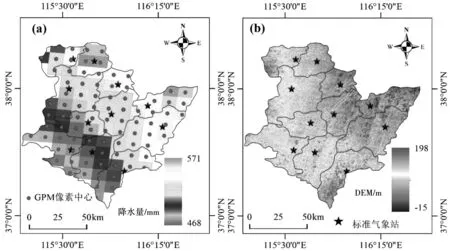
图1 研究区GPM原始产品和DEM空间分布图
1.2 数据来源
本研究主要数据为GPM卫星反演的降水量数据、地面气象观测资料和DEM数据。GPM(Global Precipitation Measurement Mission) 即由美国和日本共同研发全球降水观测计划,其降水产品为GPM卫星观测降水量融合多源对地观测卫星资料反演而成,空间精度达到0.1°(约10 km),该数据从美国航空航天局数据网站获取(https://pmm.nasa.gov/data-access/downloads/gpm)。本研究以GPM数据为降尺度源。
我国季风区降水呈现显著的经度、纬度和垂直地带性规律。为准确捕捉降水分布特性,考虑以经纬度和DEM作为预测因子。其中,经度和纬度为像素值中点的坐标、DEM数据和地面观测降水资料。DEM数据来自美国和日本共同研发的ASTER(Advanced Spaceborne Theemal Emission and Reflection Radiometer Global Digital Elevation Model) 先进星载热发射和反射辐射仪全球数字高程模型,其地面分辨率达到30 m,垂直分辨率为10 m,能够准确探测地表形态变化。
地面观测资料为衡水市11个地面气象站点观测的2018年降水量数据。
1.3 Anusplin插值法
针对气候气象要素空间关联性的特点,澳大利亚学者Hutchinson基于平滑样条函数与多维协变量理论开发了移动窗口平滑的Anusplin方法。该方法的特点在于局部使用函数逼近曲线的方法,即允许引入协变量与目标之间的线性关系进行多元拟合。目前,该方法被国际气候部门广泛应用。Anusplin的主要理论如下:
zi=f(xi)+bTyi+ei(i=1,2,…,N)
(1)
式中:zi为空间位置i处气象要素值,本研究中为降水量;f为光滑函数;xi为d维样条独立变量,即i点附近气象要素值;yi为p维独立协变量,本研究中为DEM、经度和纬度;b为协变量系数;ei为随机误差。光滑函数f和系数b,利用最小二乘来确定:
(2)
式中:Jm(f)为函数f的m阶偏导;ρ为平滑参数,由贝叶斯公式的广义最大似然来确定[6-7]。
1.4 降尺度流程与数据处理
基于相关研究经验,确定以500 m的空间分辨率为本研究的降尺度目标。基于降尺度模型可移植性的假设,即首先利用Anusplin方法结合降尺度因子构建区域0.1°尺度上的GPM预测模型;然后利用Cubic方法将降尺度因子重采样至500 m分辨率;最后将前述模型带入精细尺度的降尺度因子进行空间预测,进而得到区域500 m像素水平的降水量数据。本研究中GPM数据的空间统计、DEM数据空间分析、降尺度因子解算和空间制图均通过ArcGIS 10.8 平台完成,基于Anusplin方法的衡水市GPM数据降尺度通过Anusplin 4.2软件实施。
2 结果与分析
2.1 衡水市GPM产品统计特征
2018年衡水市GPM产品共224个降水栅格像素,利用ArcGIS空间统计工具,计算得到衡水市GPM产品空间统计特征,见表1。由表1可知,该年度GPM反演的区域降水量介于468~572 mm之间,平均值为536 mm,变异系数(CV)为0.44,在0.1°像素水平上为中等空间变异。利用Kolmogorov-Smirnov 检验表明,其双尾sig为0.01,并未通过0.05水平阈值,表明其不符合正太空间分布。后续将其利用Log函数进行转换,使其符合正态分布。

表1 衡水市2018年GPM产品空间统计特征
2.2 衡水市GPM产品与降尺度因子的关系
根据研究区GPM降水量栅格像素中心点位,采用多值提取值点的方法分别提取相应像素位置上的经纬度和DEM信息,利用线性分析方法得到二者间的关系,见图2。由图2可知,衡水市GPM降水量与地理经度之间呈现正相关关系,并在0.05水平上达到显著性,二者间拟合关系为y=71.253x-7 732.8,表明区域GPM像素值呈现自西向东增加的格局,这与图1(a)所示结果一致。其与地理纬度之间的关系为y=61.344x-1 797.5,亦呈现显著正相关关系,表明GPM降水量随着纬度增加而增加,这与我国东部季风区降水分布的纬向地带性规律不一致,主要是因为研究区尺度较小,区域降水的经度地带性规律掩盖了其纬向分异。衡水市GPM降水量值与DEM之间呈现显著负相关关系,拟合关系为y=-3.189 8x+569.51,表明区域降水随着海拔升高而减小。综合来看,GPM降水量与经度、纬度和DEM之间存在密切线性关系,因而可以作为降尺度因子进行建模分析。

图2 衡水市GPM降水量与经纬度、海拔的线性关系散点图
2.3 基于GPM数据的衡水市降水量降尺度效果
利用Anusplin模型与降尺度因子生成研究区500m像素水平的降水量空间分布图见图3。图3中表明,其空间像素值介于425~620 mm,值域范围相对于原始GPM产品有一定扩大,但其空间平均值为541.23 mm,与后者相差不大。对比图3(a)和图1(a)可知,降尺度后的GPM数据与原始GPM数据保持了良好的空间趋势性,均呈现自东北向西南减少的分布格局;降尺度后的数据更具空间细节性,展示了区域降水量分布的渐变性。该精细的降水量空间数据可为区域水资源调度、气象资源利用提供准确资料。为厘清降尺度后的误差分布,以GPM数据降尺度前后的差值为基础,再运用Anusplin模型生成空间误差分布,结果见图3(b)。由图3中表明,降尺度误差分布存在空间变异性,在研究区北部局部、东南和西部存在一定程度低估,低估范围介于-20~0 mm;而其他大部分地区为高估,高估范围介于0~34 mm之间,其中低估中心与高估中心邻近分布在区域北端。

图3 研究区GPM产品降尺度效果和误差空间分布图
2.4 Anusplin模型验证结果
计算原始GPM产品与降尺度后的数据之间的一致性,结果见图4(a)。统计得到二者之间的拟合关系为y=1.033 5x+0.350,R2为0.90,MAE和RMSE仅为17.73和20.58 mm,表明降尺度后的数据依然保持了原始GPM产品的空间精度,具有较低的误差,也说明降尺度结果的可靠性。为验证该模型的鲁棒性,以研究区2019年11个地面站点观测降水量为参考值,测试其实际精度,结果见图4(b)。图4(b)中显示,GPM降尺度值与实际降水量之间存在较小误差,R2达到0.96,MAE为16.74 mm,RMSE为19.77 mm,显示出预测者与观测值之间高度一致性,同时也表明该模型具有稳健性和可移植性。

图4 研究区降尺度前后散点图
3 结 论
经过降尺度后,GPM产品空间分辨率由0.1°提升至500 m,并且保持了原始数据精度,从空间上能展示更多细节信息,这对描述区域降水量分布极具优势。本研究的降尺度模型适用于衡水市。但仍需关注的是,影响降水量分布的因素不仅是经纬度和地形,大气含水量、地表覆被、季风特性也是重要的降尺度的因子,这些在后续的研究中应予以考虑。
