基于周期自适应学习的中低速磁悬浮列车运行控制方法
2021-07-30张文静曹博文李孟月徐洪泽
张文静,南 楠,曹博文,李孟月,岳 强,徐洪泽
(北京交通大学 电子信息工程学院, 北京 100044)
磁悬浮列车是一种利用电磁力实现悬浮、导向与驱动的新型轨道交通工具,有望成为21世纪的主要交通方式之一。与传统轮轨列车相比,磁悬浮列车具有振动小、运行噪音低、转弯半径小、抗风化能力强、寿命长等优点[1]。此外,由于采用非接触式运行方式,磁悬浮列车取代了轮轨交通的轮轨接触支撑结构,无附着力限制,爬坡能力更强。随着上海磁悬浮试验线、长沙机场快线和北京S1线的相继开通,磁悬浮交通的运行控制成为轨道交通理论研究领域的热点问题。
运行控制系统OCS(Operation Control System) 是保证磁浮列车正常运行的中枢系统,是磁浮列车运行控制的“大脑”和“神经系统”,主要作用是运行指挥和安全防护。运行控制算法是OCS的核心技术之一,然而目前的磁浮运行控制系统借鉴CBTC (Communication-Based Train Control System)系统,尚无成熟的运行控制算法。因此,研究磁悬浮列车运行控制算法,提高磁浮列车运行控制性能,具有重要的意义。
文献[2-3]提出了不同的控制方法,有效地提高了轮轨列车的运行性能。文献[4]结合专家经验和梯度下降法,设计了一种基于在线调整方法的智能驾驶算法,提高了列车运行性能。文献[5]改进了传统的列车动力学模型,利用遗传算法修正不同运行条件下的阻力系数,通过将分数阶PID控制器引入列车运行控制,实现了更好的速度控制效果,提高了控制精度。为提高列车自动驾驶ATO(Automatic Train Operation)系统速度控制的精度与鲁棒性,文献[6]提出了一种基于模糊PID的ATO控制算法。针对列车停车阶段的重复性和涉及多目标的特性,文献[7]引入迭代学习控制ILC(Iterative Learning Control),提高了列车停车精度与舒适度。以上均为基于轮轨交通系统的运行控制方法。然而,磁悬浮列车与传统轮轨列车的牵引方式不同,其运行控制方法存在较大差异,现有成熟的轮轨列车运行控制方法并不适用于磁悬浮列车。
近年来,研究学者们将ILC用于重复作业对象,利用先前迭代或周期信息不断修正当前迭代或者周期的控制器输出,随着迭代次数的增加,系统可以在有限时间内精确跟踪期望轨迹[8-10]。文献[11]提出了一种基函数型自适应迭代控制方法,提高了迭代学习控制下非最小相位系统的位置跟踪精度。文献[12]设计了一种约束自适应边界迭代学习控制律,解决了周期边界扰动下Euler-Bernoulli系统的振动控制和输入约束问题。在文献[13-15]中,针对具有周期扰动或具有周期性状态变量的控制系统,引入周期自适应学习控制(Periodic Adaptive Learning Control,PALC),取得了较好的控制效果。文献[16]利用PALC算法补偿电机系统中状态相关的非Lipschitz周期扰动,实现了高精度的位置跟踪。文献[17]结合线性扰动观测器和周期自适应学习的优点,提出了一种周期学习扰动观测器,有效补偿了永磁同步直线电机中的非线性干扰。文献[18]针对永磁同步位置伺服系统中的周期性扰动补偿问题,设计了一种双高阶周期自适应学习补偿方法,提高了系统的位置跟踪性能。文献[19]利用PALC算法及饱和补偿器,实现了饱和输入非线性系统的高精度位置跟踪控制。
中低速磁悬浮列车运行速度较低(≤160 km/h),主要阻力来源于涡流阻力和特殊线路段的线路附加阻力。由于线路的坡道和弯道是固定的,当列车在指定线路往返运行时,所受运行阻力具有周期性。通过分析列车动力学模型,本文将周期自适应学习引入列车运行控制,提出一种基于周期自适应学习的列车运行控制方法。控制器包括4个部分:PD控制模块、速度前馈模块、涡流阻力与空气阻力补偿模块和周期自适应线路附加阻力补偿模块。本文所提出的运行控制方法的核心是:利用PALC算法估计运行过程中的线路附加阻力,在控制器中加入相应的控制力(包括牵引力和制动力),消除线路附加阻力对列车运行的影响,提高列车运行的性能。仿真结果验证了本文所提控制算法的有效性与鲁棒性。
1 中低速磁悬浮列车运行控制问题描述
根据牛顿运动定律,在磁悬浮列车运行过程中,列车所受合力满足[20]
ma=u-fair-feddy-fi-fr
(1)
式中:m为列车质量;a为列车加速度;u为列车牵引力或制动力;fair为列车运行过程中所受到的空气阻力;fi和fr分别为坡道附加阻力和弯道附加阻力;feddy为线路F轨与悬浮电磁铁间的涡流阻力。
列车运行过程中,所受空气阻力与列车车体的最大横截面积、阻力系数、空气密度以及列车速度有关,可表示为
(2)
式中:v为列车速度;N为列车编组车辆数。
悬浮系统的电磁铁芯由硅钢薄片叠压而成,其涡流效应可以忽略不计。涡流阻力主要来自于线路两侧的F轨与悬浮电磁铁之间的涡流效应,计算式为
feddy=N(0.1v0.5+0.02v0.7)
(3)
当磁悬浮列车经过坡道线路时,坡道附加阻力大小由坡道坡度决定,可表示为
fi=iNmgsgnφ
(4)
式中:i为坡道坡度的千分度;g为重力加速度。当sgnφ>0时,表示列车处于上坡状态,fi>0;当sgnφ<0时,表示列车处于下坡状态,fi<0。
此外,当列车运行于弯道线路时,所受的弯道附加阻力可表示为
(5)
式中:R为弯道线路曲线半径。
考虑如下的中低速磁悬浮列车动力学模型
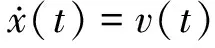
(6)
(7)
式中:x(t)为列车位移;fres[x(t)]sgn[v(t)]是磁悬浮列车在运行过程中受到的线路附加阻力,包括弯道附加阻力与坡道附加阻力,不考虑管道附加阻力。
假设1 当列车的运行控制性能较高且沿固定线路往返运行时,列车的位置与速度均有相同且固定的周期Pt,且Pt可以准确获得,列车的位置与速度满足xd(t+iPt)=xd(t),vd(t+iPt)=vd(t),x(t+iPt)≈x(t),v(t+iPt)≈v(t),i∈Z+。
性质1 在列车运行过程中,所受线路附加阻力的大小与列车实际位置x有关。根据假设1,线路附加阻力fres满足:fres(t+iPt)≈fres(t),i∈Z+。
为了提高列车运行控制性能,利用列车运行和运行阻力共有的周期特性,本文提出一种基于周期自适应学习的列车运行控制方法。
2 周期自适应学习控制器设计
通常,列车在指定线路第一次往返运行时,驾驶员可以利用驾驶员控制台(Driver Control,DC)显示的线路信息(包括线路最高限速、列车当前速度等)和车辆状态,依据实际情况进行操作,实现手动驾驶。从列车第二次往返开始,利用前一周期的信息和PALC算法,估计运行过程中的线路附加阻力。
(1)实际的列控系统为复杂、多目标的非线性动力系统,为保证第一周期系统稳定,让有长期驾驶经验的司机驾驶,可以实时有效地控制列车满足多项要求[2]。

ex(t)=x(t)-xd(t)
(8)
(9)
e=ev(t)+λex(t)
(10)
式中:λ为待调节正参数;ex为位置误差;ev为速度误差。
(11)
为了消除运行阻力对系统的影响,针对运行阻力中的未知参数fres(x),结合自适应理论与列车运行的周期特性,本文设计了周期学习自适应控制器为
(12)
式中:α为待设计正参数。


图1 PALC自适应控制律结构框图
从第2个周期开始,利用周期自适应更新律,开始学习未知参数fres为
(13)
式中:kres为待设计周期自适应增益;P(t)为列车运行周期。
为证明系统的稳定性,构造Lyapunov函数为
(14)
计算V(t)在周期区间[t-Pt,t]的差分为
(15)
为使计算过程清晰,令式(15)右边第一项为A,第二项为B,即
(16)
(17)
由式(7)和式(9)可知
(18)
由式(10)和式(12),可得
(19)
将式(19)代入式(16),A简化为
α(ev+λex)2]dτ
(20)
由列车运行的周期性和性质1,可得
(21)

将式(20)和式(21)代入式(15),化简可得
ΔV=A+B=
(22)
代入自适应更新律式(13),式(22)右边第二项等于0。因此,有
(23)

3 仿真验证
利用某中低速磁悬浮试验线数据进行仿真研究,通过与传统PID控制器的对比,验证所提出算法的优越性和有效性,试验线路见图2,试验线车辆参数见表1。

图2 中低速磁悬浮列车试验线路(单位:m)

表1 车辆与线路参数
3.1 参数调节
仿真时,PALC控制器和PID控制器的参数调节过程如下
Step1线性参数调节。综合考虑系统快速性和平稳性,利用MATLAB工具箱整定PALC控制器和PID控制器参数,结果见表2。

表2 PALC和PID控制器的线性部分参数
Step2自适应参数调节。理论上,自适应参数可选择任意正数,数值越大,收敛速度越快,跟踪误差越小。然而,过大的参数会导致系统震荡甚至不稳定。因此,综合考虑系统的收敛速度、稳定性和跟踪误差,通过多次调节,选择使PALC控制器控制效果最佳的自适应参数为kres=2×1012。
3.2 仿真验证
在仿真中,令初始状态为零,从第二个周期开始,利用周期自适应更新律,对线路附加阻力进行估计。设置仿真中列车单程运行距离1.58 km,最大加速度为0.9 m/s2,往返周期Pt=178 s,仿真步长T=10-5s。
设置的期望速度-位置曲线见图3,期望位置曲线xd、PID控制器和PALC控制器的位置跟踪轨迹见图4,PID控制器和PALC控制器的位置跟踪误差见图5。可以看出,由于存在线路附加阻力,PID控制器的最大位置跟踪误差为3.12 m。PALC控制器充分利用了列车往返运行过程中的周期信息,在16个迭代周期后,最大位置误差仅为0.03 m,从图5中可以看出,PALC控制器具有更好的位置跟踪性能。

图3 期望速度-位置曲线
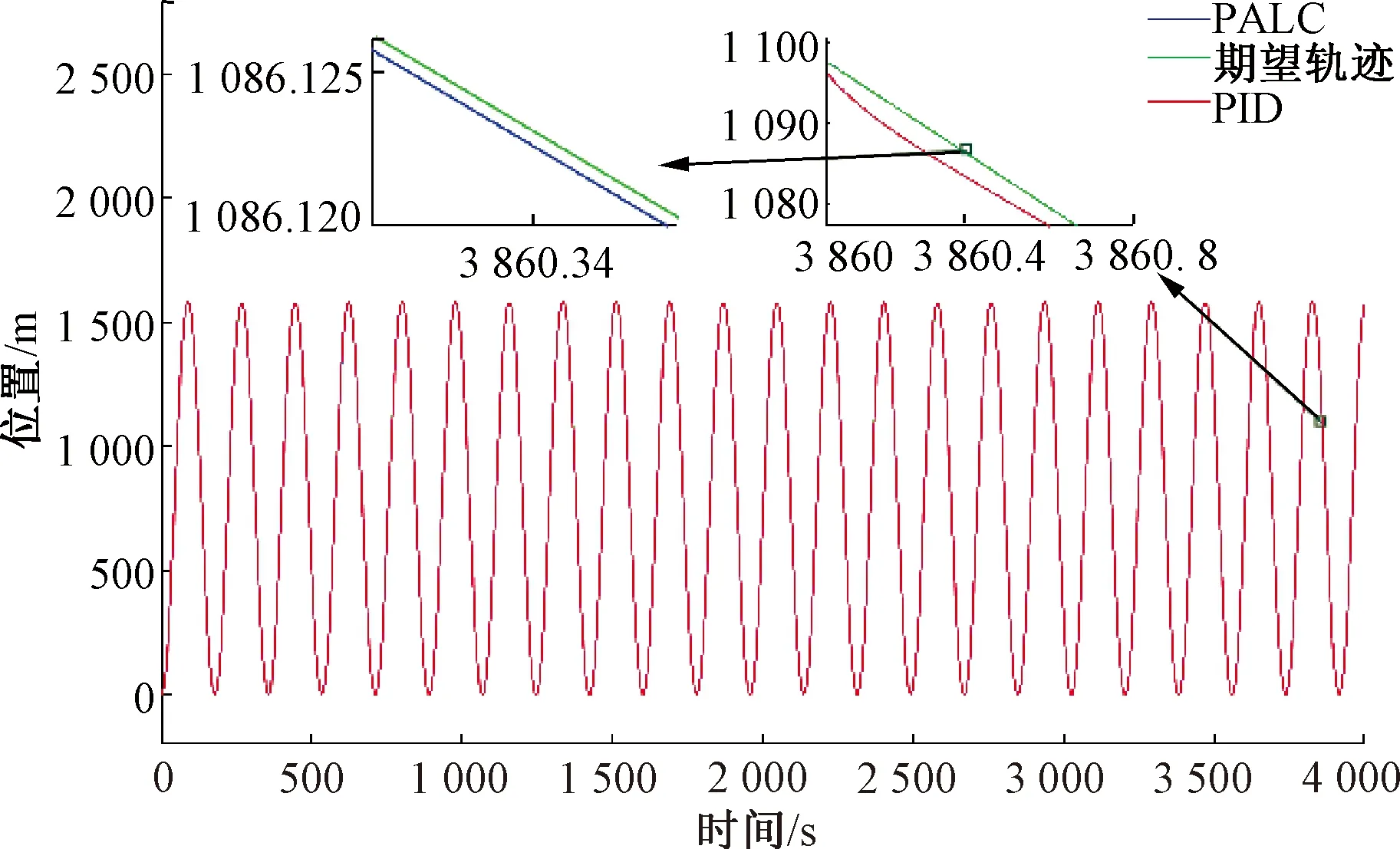
图4 期望位置曲线及PALC控制器和PID控制器的位置跟踪曲线

图5 PALC控制器和PID控制器的位置跟踪误差
PID控制器和PALC控制器的速度跟踪以及速度跟踪误差曲线分别见图6和图7,在不同线路的速度跟踪误差列于表3。从仿真结果可以看出,在平直线路,由于仅存在涡流阻力,PALC和PID控制下的速度跟踪性能差别不大。然而,在弯道线路与坡道线路,相对于PID控制器,由于PALC控制器补偿了线路阻力,其速度跟踪性能更好。另外,从图6可以看出,PALC控制下的列车速度跟踪曲线更加平滑,列车运行更加平稳,舒适性更好。

图6 PALC控制器和PID控制器的速度曲线

图7 PALC控制器和PID控制器的速度跟踪误差
PALC算法估计的附加阻力和真实线路附加阻力见图8。可以看出,在16个迭代周期后,PALC控制器成功的估计了线路附加阻力。

图8 实际附加阻力和PALC算法估计线路阻力
PID控制器和PALC控制器的控制输出曲线见图9。由图9可以看出,经过16个迭代周期,PALC控制器输出稳定。PALC控制器和PID控制器下列车在第17个运行周期内的能耗曲线见图10。由图10可以看出,与PID控制器相比,PALC控制器控制下的磁浮列车,不仅位置跟踪性能更优,而且能耗降低了0.2%。

图9 PALC控制器和PID控制器的输出

图10 第17个运行周期内的列车运行能耗曲线
为了验证所提出算法的优越性,利用位置误差的ITAE指标,比较PALC控制器和PID控制器的位置跟踪性能,结果见图11。由图11可以看出,PALC算法消除了线路附加阻力对列车位置跟踪性能的影响。

图11 PALC控制器和PID控制器的位置误差ITAE指标
为了进一步检验本文所提PALC算法的鲁棒性,在控制器参数不变的情况下,加入能量谱密度为1012的白噪声干扰。噪声干扰下的位置跟踪误差、速度跟踪误差、控制器输出以及线路附加阻力估计曲线见图12。从图12中可以看出,加入噪声干扰后,列车在PID控制器和PALC控制器下的最大位置跟踪误差分别为3.22、0.01 m,在不同线路区段最大速度误差跟踪见表4。对比无噪声干扰下的仿真结果,PID控制下的列车速度与位置跟踪性能明显变差,而PALC控制下的列车速度与位置跟踪性能下降很小,表明PALC控制器有较强的鲁棒性。

表4 噪声干扰下不同线路区段的最大速度跟踪误差 m/s

图12 噪声干扰下PALC控制和PID控制的位置跟踪误差、速度跟踪误差、控制器输出及线路附加阻力估计曲线
4 结论
针对中低速磁悬列车的位置控制问题,本文考虑列车在指定线路运行的周期特性,提出了基于周期自适应学习的运行控制算法,消除了运行阻力对列车运行过程的影响,提高了列车位置控制的性能。该控制方法包含4部分:PD部分保证系统满足基本控制要求,前馈部分改善了系统瞬态响应,周期自适应补偿部分实时估计线路附加阻力,空气阻力与涡流阻力补偿部分进一步提高了列车的位置跟踪性能。仿真结果表明:本文所提出的周期自适应运行控制方法能够有效提高中低速磁浮列车运行的位置控制精度,控制算法具有较强的鲁棒性,而且能耗更低。
