复合函数求导法则教学方法探讨

胡效华

（北京信息职业技术学院 北京 100070）

复合函数求导是导数运算中重要一环，它的链式求导法则即是导数运算学习的重点.也是学习的难点。

在七年制高职学生的微积分学习过程中，针对学生的年龄特点，复合函数求导法则教学中应把握以下几点：

一、牢记基本初等函数及其求导公式

二、能正确分解复合函数，分清中间变量与自变量

一般地，对于两个函数y=f(u)和u=g（x） ，如果通过变量u，y可以表示成x的函数，那么称这个函数为函数y=f(u)和u=g（x）的复合函数，记作y=f(g(x)),其中u叫做中间变量。

复合函数求导，关键在于能够正确分解复合函数。这就要求学生能够理清函数的复合结构，由外及里，一层一层的分解函数。教学过程中，可以指导学生这样看待复合函数，即注意等号右端的小括号，将小括号看作中间变量，没有小括号的，需要自己判断并补出小括号[1]。复合函数是否分解正确，所分解出的函数应是基本初等函数或者基本初等函数与常数经过四则运算得到的函数。要做到不漏、不重。简单的复合函数常见题型如下表。

?

三、记住复合函数的求导公式

复合函数y=f(g(x))的导数和函数y=f(u)和u=g(x))的导数间的关系为 ，即yx′=yu′·ux′对y的x导数等于y对u的导数与u对x的导数的乘积.

利用复合函数求导公式做题，第一步分解复合函数，第二步计算yu′与ux′，第三步计算yx′=yu′·ux′并还原u。从解题步骤可以看出，分解复合函数是关键，导数基本公式是基础，复合函数求导法则是应用[2]。

对于前边给出的复合函数，其求导过程如下表（适合于常见的简单复合函数求导题型）：

?

有的时候，我们会遇到由三个或三个以上的函数复合而成的函数，此时应用复合函数求导法则，就要像剥洋葱似的，由外及里，一层一层“剥皮”，将函数分解成基本初等函数的形式，再逐层求导、求各导数的乘积，还原中间变量，得到结果。

举例如下：

求y=1n[sin(x-1)]的导数。

解1，设y=1nu,u=sinv,v=x-1

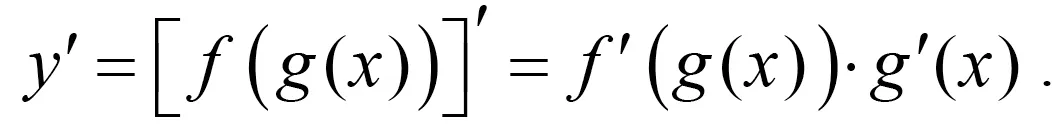
比如，求y=(2x-3)3的导数。

解：y′=3(2x-3)2.(2x-3)′=3(2x-3)2.2=6(2x-3)2′.

求y=1n[sin(x-1)]的导数也可以这样解：

此种方法，不设中间变量，而是用“心算”方法完成求导过程，要达到这样心算的程度，需要熟练掌握基本求导方法，方能形成求导的速度与技巧。