在课时教学中落实核心素养——以“根式”为例

韩小波

（南京市溧水第三高级中学，江苏 南京 211200）

一、问题的提出

《普通高中数学课程标准（2017年版）》要求高中数学教学应以发展学生数学学科核心素养为导向，并明确指出，在教学活动中，教师应准确把握课程目标、课程内容和学业质量的要求，合理设计教学目标，通过相应的教学设施，结合相应的教学内容，落实“四基”，培养“四能”，在学生掌握知识技能的同时，促进学生数学学科核心素养的提升。

二、“根式”教学设计

以下教学内容选自苏教版高一《数学》必修一第二章第二节“指数函数”的第一课时。

（一）教学内容分析

“根式”是指数函数的第一课时，它对学生理解指数运算知识有着非常重要的意义，可以为后续指对数的逆运算打下坚实的基础。这一课时的重点是让学生理解根式的意义和根式的性质。

（二）确立教学目标

目标一：教师通过细胞分裂和经济发展十年翻一番等实例，引出这章节的主要内容，让学生联想方根的概念，感受乘方与开方的互逆关系。

目标二：教师通过平方根、立方根的复习，引入四次方根、五次方根的定义，进而推出n次方根的定义，得出根式的概念。学生从类比猜想到数学表达，体会用乘方定义开方，用乘方运算完成开方运算的过程，为后期函数的学习做铺垫。

（三）学情分析

学生在初中阶段学过平方根、立方根，所以对开方有一定的认识，并且知道正数有两个平方根，负数只有立方根，但对根式的概念比较模糊。

（四）教学过程设计

环节一：情境引入

引例一：细胞分裂时，每次每个细胞会分裂成2个细胞，也就是说，第一次分裂时，1个细胞会分裂成2个细胞；第二次分裂时，2个细胞会分裂成4个细胞；第三次分裂时，4个细胞会分裂成8个细胞……假设第x次分裂会得到y个细胞，那么细胞个数y与次数x之间有何关系？

“根式”是学习指数函数的第一步，此例旨在向我们介绍生活中存在的不同变量关系，以及我们要学习的新函数——指数函数，这是对函数概念和性质的进一步研究、深化与扩展。

引例二：邓小平同志提出中国经济发展“三步走”方针：第一步，从1981年到1990年，国民生产总值翻一番，解决人民的温饱问题；第二步，从1991年到20世纪末，国民生产总值再翻一番，人民生活达到小康水平；第三步，到21世纪中叶，人均国民生产总值达到中等发达国家水平，人民生活比较富裕，基本实现现代化。

这里涉及一个数学问题：“十年翻一番，平均每年要增长多少呢？”假设每年平均增长量为p，1981年的国民生产总值记作1，则有（1+p）10=2，1+p叫作底数，10是指数，2是幂，如何求p呢？教师应该提出数学问题，引导学生思考，即当x10=2时，如何求出x？

环节二：问题驱动，回忆过往

问题一：（1）若x2=2，则x=（2）若x3=2，则x=

（3）5的平方根是_____（4）-3的立方根是____

以上问题是平方根、立方根的两种表述，学生由此回忆出平方根、立方根的定义，再通过平方和立方的定义，理解平方根和立方根的含义。

当学生回忆平方根、立方根的定义及相关知识时，教师可以用投影给出追加问题。

追加问题意义在于让学生充分理解根式的概念。

环节三：问题驱动，类比延伸

问题二：（1）若x4=16，则x=（2）若x4=7，则x=

基于平方根、立方根的定义，学生能够类比出四次方根的定义，即用乘方定义开方。给出追加问题。

（3）16的四次方根是____（4）7的四次方根是____

利用追加问题进一步理解方根的运算是如何利用乘方运算完成的。

再次理解根式的概念，只有正数才有偶次方根，负数没有偶次方根。

问题三：（1）若x5=-32，则x=（2）若x5=9，则x=

用前面的思路进一步定义五次方根。

（3）-32的五次方根是____（4）9的五次方根是___

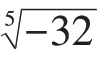
再次理解根式的概念及五次方根的表示方式，利用乘方运算完成开方运算。

思考：若xn=a（n≥2且n∈N），则x=

教师让学生总结出n次方根的定义。给出追加问题。

（1）36的六次方根是___（2）（-2）7的七次方根是___

旨在巩固n次方根，理解方根的运算仍然通过乘方运算来完成。

环节四：连锁问题，构建新知

教师提出根式的概念。

思考：n次方根和根式的区别与联系

三、教学启示

（一）吃透教材，理解教学内容

本节课主要是通过n次方根理解根式的意义，虽然内容简单，但其蕴含的道理很深。本课运用了乘方思想定义开方，又运用了乘方运算完成开方运算，让学生认识到乘方和开方是逆运算，正如加、减，乘、除运算一样，为后续对数的学习与运算做了很好的铺垫。在课堂教学中，教师通过一系列问题引发学生思考和探究，将学生的思维引向深处。本节课的知识脉络如图所示。

（二）精心设计

要想提升学生的学科核心素养，教师应结合结果性知识与过程性知识的讲解。数学教师要摒弃传统的“灌输式”教学，通过精心设计，将知识的形成和发展过程呈现给学生，带领学生分析各知识点之间的联系、延伸思路，将蕴含在教学内容中的核心素养提炼出来，再渗透给学生。

本节课蕴含了两个核心素养：数学抽象和逻辑推理。在核心素养的落实上，教师的引导极其重要。在教学前，教师需要思考：课堂教学的“四基”体现在知识发生、发展的过程，可以提出解决问题的思想方法；“四能”体现在发现、提出、分析和解决问题的过程，离不开知识性任务的学习，然后达到“三会”。在教学过程中，教师要启发学生主动提出问题，这既是重要的研究方法，又是培养学生发现问题、提出问题的重要契机。教师需要及时追问、反问学生是否还有其他的想法，鼓励学生敢于质疑。这种理性的意识、缜密的思维、质疑的精神是教书育人的本质所在。最后，教师要让学生学会小结，养成良好的学习习惯。学生核心素养的提升需要我们用心、用情、用智慧，守正笃实，久久为功。