基于R-Vine Copula模型的国际原油与国际股市间的风险传染效应研究

□邹辉文 朱丽娟

[福州大学 福州 350116]

引言

国际原油市场作为全球性的资源商品市场，加上其金融投资属性，汇集了世界各地的投资主体。因此，当能源市场价格剧烈波动时，极易在世界范围内引起波澜。2020年初，在美国、沙特及俄罗斯等国家之间“非理性价格战”的影响下，国际油价崩盘，全球股票市场纷纷遭遇重创[1]。在此背景下，研究国际原油市场与国际股市之间的风险传染效应，明确国际原油市场与国际股市之间的整体联动关系对投资者及时判断市场走向提高能源意识以及各个国家防范能源安全与金融安全等都具有重要的现实意义。

为更好地理解油价与经济之间的联系，许多学者对油价与股票等其他交易资产之间的关系展开了不同的研究。油价变动会直接影响有关企业的生产成本、经营利润乃至未来现金流，进而导致微观个体股价波动。因此，部分学者从微观视角，研究油价波动对油气公司的股价或者相关行业股票市场的影响[2～4]。相应地，其他学者则从宏观视角入手进行研究。如李丽红指出能源金融市场的价格波动风险，经由市场间的信息、资产、资金等渠道可以传导至国际金融市场[5]。国际原油的价格变动在产出、消费、通胀预期等因素的影响下，使得经济不确定性增加，间接影响了股票市场。金洪飞和金荦发现国际原油价格与美国股市之间存在双向波动溢出，而对中国股市则没有明显的溢出效应[6]。Amalia和Purqon则指出了油价波动对印度尼西亚股票价格的影响[7]。其他学者在研究体系中加入了更多的国家进行探究，如朱慧明选择油价对金砖五国的股市影响进行研究[8]。陈晓春和黄媛指出国际原油市场与亚太股票市场的正向联动关系[9]。Degiannakis认为石油和股票市场之间的因果关系在很大程度上取决于研究是使用总股票市场指数、行业指数还是公司层面的数据，以及股票市场是在净石油进口国还是净石油出口国运作[10]。最后，在油价变动对股票市场影响的具体研究方法中，现有研究中主要有两种思路：一是在股票定价的多因子模型中引入油价作为影响因子之一，探究油价对股票价格的解释程度[11]；另一种是采用VAR[12～13]、GARCH族[14～15]等模型探究油价波动与股市之间的溢出效应。

综合现有研究，可以发现国际原油市场与国际股市之间存在一定的关联，且油价变动产生的影响在不同经济体特别是依赖原油进出口的经济体之间存在差异。在现有研究中，学者们更倾向于单独将原油市场与不同股市两两建模进行分析，以直观地反映油价波动对一国股市的影响程度。但实际上，当研究框架中的国际市场逐渐增加时，我们不仅要考虑能源市场与金融市场之间的溢出关系，也要考虑金融市场之间可能出现的风险外溢情况。基于以上认识，区别于以往研究，本文可能的边际贡献在于：（1）考虑油价波动期间，各个国家股市之间也可能存在的风险溢出情况，对国际原油市场与国际股市的整体联动做出判断；（2）为更好地刻画国际原油市场与不同国家股市之间的风险传染路径，本文在不同市场间引入更为灵活的R-Vine Copula模型进行研究。Vine Copula模型是在二元Copula模型的基础上，进行逐层叠加，并通过一定路径将不同变量之间的相依结构反映出来的图模型[16]，在刻画风险传染路径方面具有广泛应用[17～19]。

一、R-Vine Copula模型

Copula函数是在Sklar[20]定理基础上，延伸得到的一种能够连接边缘分布与联合分布的函数。在实际研究中，为得到不同个体之间的复杂相依结构，经常将不同个体的风险用边缘分布来刻画，经由不同Copula函数连接，得到整体的联合分布，并以联合分布反映整体风险。但在此过程中，随着参与个体的增加，多元Copula模型中很容易出现“维数灾难”。基于此，Bedford和Cooke提出了Vine Copula（藤Copula）模型[21]。并在C-Vine Copula和D-Vine Copula模型的基础上，为提高模型的灵活性，弱化条件独立概念，Bedford等又提出了R-Vine Copula模型[22]。结合文献[23]，一个m变量的R-Vine Copula模型描述如下：

一个m变量的R藤由（m−1）棵树组成，记成T1,T2,···Tm−1,第i棵树Ti的节点集为Ni，边集为Ei(i=1,···,m−1)，它们满足如下条件：

1.树T1的节点集N1={1,···m}，边集为E1；

2.第i棵树Ti的节点集Ni=Ei−1(i=2,···m−1)，即第i棵树的节点集是第（i−1）棵树的边集；

3.如果树Ti中的两条边在树Ti+1中用边连接，那么这两条边在树Ti中必须有一个共同的节点。

进一步构造一个m元R藤结构如下：

设由m个随机变量X1,X2,···Xm构成的随机向量为X={X1,X2,···Xm},其中第i个变量Xi的边际密度为fi(i=1,···m)，则X的联合密度函数可以表示为：

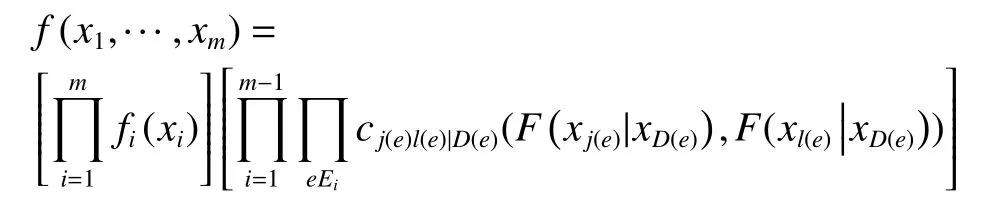
在上述式子中，Ei中的边e=j(e)l(e)|D(e)，j(e)与l(e)是边e相连接的两个节点，D(e)是条件集。cj(e)l(e)|D(e)表示边e对应的Copula密度函数。xD(e)表示由条件集D(e)决定的子向量。

二、实证分析

（一）研究对象

在国际油价与股票市场的关联研究中，许多学者以原油期货价格作为油价代表[6,13]。并且，WTI原油价格是国际油价的定价基准。因此，借鉴张曦和王剑雨[13]的做法，本文的国际原油价格以WTI原油期货价格作为代表。此外，对于国际股市的选择，参照朱慧明等[24]的标准，从原油进出口依赖度较高的国家中，择优选取金融市场较为完善的国家进行研究。本文最终选取了15个国家作为研究对象。分别是8个原油进口国：中国（CHN）、美国（USA）、日本（JPN）、德国（GER）、法国（FRA）、英国（UK）、韩国（KOR）和印度（IND），以及7个原油出口国：沙特阿拉伯（KSA）、俄罗斯（RUS）、阿联酋（ARE）、加拿大（CAN）、墨西哥（MEX）、尼日利亚（NGA）和挪威（NOR）。进一步选择上述国家的股票指数进行研究。本文最终选择的国家股票指数如下：中国上证综指、美国标准普尔500指数、日本东京日经225指数、德国法兰克福DAX指数、法国巴黎CAC40指数、英国富时100指数、韩国综合指数、印度孟买Sensex指数、沙特全股交易指数、俄罗斯RTS指数、阿联酋DFM综合指数、加拿大标普TSX60指数、墨西哥MXX指数、尼日利亚综合指数和挪威OBX指数。

（二）研究数据

鉴于2020年国际公共安全事件更为突出，不利于单独衡量油价波动对国际股市带来的影响，故选取2010～2019年上述国家股票指数的日收盘价以及WTI原油期货每日价格进行观察（图1）。考虑到各国假期差异，在原始数据中剔除部分观测值，利用匹配的日数据进行分析。其中，原油进口国国家指数日收盘价数据来源于同花顺，WTI原油期货价格以及原油出口国国家指数数据来源于Wind数据库。

图1 2010～2019年国际油价与原油进口国国家股票指数

下面先分析国际原油与主要原油进口国股市之间的关系。首先观察WTI原油期货价格与原油进口国国家股票指数收盘价之间的波动情况。

对比国际油价与各主要原油进口国的国家指数，直观地看油价波动对原油进口国股市是有一定影响的。特别在2014～2016年，国际油价巨幅下跌，随后各个国家股市也呈现出振荡下滑的趋势。但是油价波动与股市之间的具体关系仅由资产价格的联动是无法确定的。下文将在此基础上做进一步研究。

结合图1，拟选取2014年6月20日～2016年1月19日（油价剧烈下浮期间）的数据做进一步研究。为消除价格波动对价格水平的依赖关系，对上述资产价格或指数序列做如下转换：

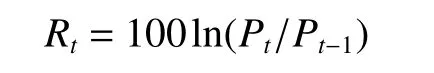
其中，Pt为t时刻的国家指数收盘价（或WTI原油期货价格）序列，Rt为转换后的收益率序列。对各收益率序列做描述性统计分析如表1所示：

表1 各收益率序列的描述性统计分析

根据表1的描述性统计，可以发现各收益率序列的均值总体上都在零值左右。此外，结合JB统计量可以发现，所选的收益率序列均拒绝接受服从正态分布的假设。且各序列的偏度多为负，峰度显著大于3，说明数据序列为非对称分布，并呈现尖峰肥尾的特征。对数据进行ADF检验的结果显示，所有序列均平稳。但ARCH-LM检验则显示除德国法兰克福DAX指数和印度孟买Sensex指数收益率序列外，其他序列均都存在显著的条件异方差，因此需要进一步构建有关模型（常见的GARCH类模型）进行过滤。

（三）模型构建

根据Sklar[20]定理，Copula模型的构建分为两步：首先，对各随机变量进行边缘分布拟合；其次，选择合适的Copula函数对不同边缘分布进行连接。

1.边缘分布拟合

根据上文的描述性统计分析，本文所选取的数据具有尖峰肥尾的特征，并且存在显著的条件异方差。因此为更好地刻画各对数收益率序列的波动特征，并消除序列的ARCH效应，笔者分别对各个国家的对数收益率序列构建GARCH类模型进行边缘分布拟合。同时通过对比不同模型（GARCH (1, 1)-n,GARCH (1, 1)-t, GARCH (1, 1)-ged）的AIC信息准则，择优选取适合的模型。并过滤出标准化残差，得到参数估计结果见表2。

表2 GARCH（1,1）模型的参数估计结果

如表2所示，几乎所有对数收益率序列的ARCH项和GARCH项的估计参数均显著，说明所建模型能够较好地拟合各个序列，各个国家股票指数以及原油序列均存在波动聚集效应。进一步观察模型标准化残差的ARCH-LM检验结果，各个序列对应的p值均显著不为0，说明模型过滤出的标准化残差序列不存在条件异方差。在此基础上对其进行概率积分变换，使其累积分布其近似服从于[0, 1]均匀分布，并进行KS检验，以达到构建Copula模型的条件。变换后的序列均通过了KS检验，因此可以进一步构建Copula模型。

2.Vine Copula模型

得到各序列的累积分布后，接下来需选择不同序列之间连接的Copula函数。鉴于Vine Copula模型可以自动匹配合适的Copula函数，因此接下来直接建立Vine Copula模型。常见的Vine Copula模型有C藤、D藤和R藤。为选取最合适的模型，本文根据Log Likelihood统计量进行判断，最终择优选取R藤Copula模型进行建模分析。借助R软件，得到各出口国国家指数和原油收益率序列的R藤Copula相依结构模型秩相关 数如表3所示：

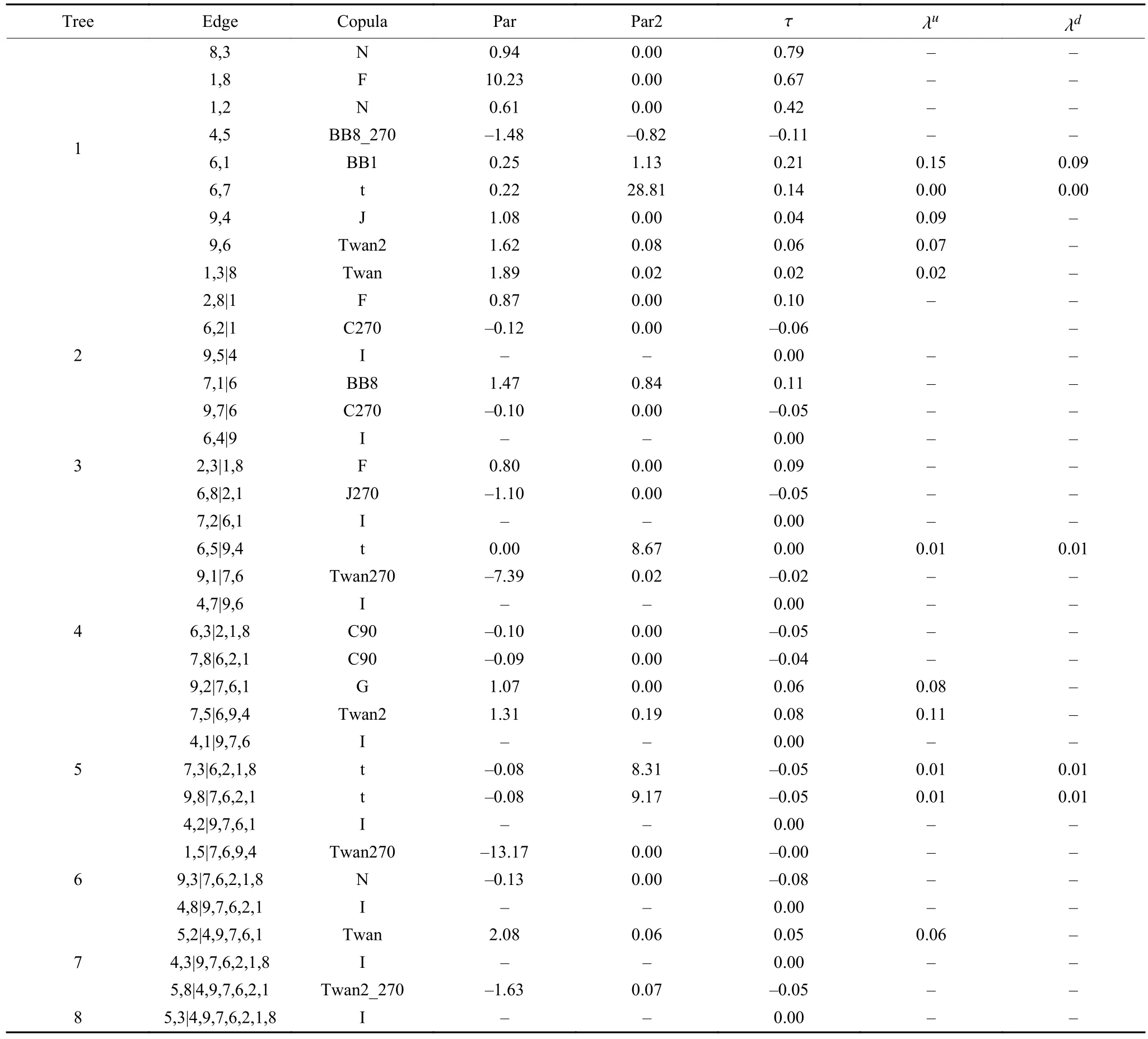
表3 模型的Pair-Copula拟合结果

分析模型的拟合结果，在所构建的模型中，9个变量一共构造出了8层树结构。其中，不仅反映出了原油与原油进口国国家股票指数之间的关联，还反映了不同国家股票指数之间的相依关系。因为一国股票市场的变动往往是由诸多因素引起的，且金融市场之间的信息传播比能源市场要快得多，所以在油价剧烈变动的冲击下，风险在国家之间的传导可能会更快于能源市场的传导。进一步地观察不同序列之间的相依结构，不同序列之间连接的Copula函数不尽相同，即使是相同的Copula函数，对应的参数也有所不同，说明原油与原油进口国国家股票指数之间的相依结构存在一定的差异性。表中的秩相关系数反映了不同序列之间的关联程度以及方向。从报告的第一层树来看，在2014年下半年油价暴跌期间，原油与印度以及韩国的国家指数呈现出了正相依性。原油与印度孟买Sensex指数之间的无条件秩相关系数为0.06，与韩国综合指数之间的秩相关系数为0.04。说明原油与印度孟买Sensex指数以及韩国综合指数容易出现同涨同跌的趋势，这一结果与图1所呈现的情况相一致。结合原油与原油进口国国家股票指数之间的Pair Copula，用线段表示不同序列之间的连接关系，画出原油与原油进口国国家指数间相依结构的第一层树形结构图（图2）做进一步分析。

图2 原油与原油进口国国家指数间的相依机构

如图2所示，在油价暴跌期间，原油在藤结构中作为一个节点，连接了韩国综合指数和印度孟买Sensex指数。当原油市场因油价巨幅波动成为风险源时，会率先向印度以及韩国的股票市场溢出。印度作为原油消费大国，在此次油价大幅度下跌期间成为产油国的目标市场之一，印度股市由此做出了一定的反映。此外，印度孟买Sensex指数本身又作为一个节点，连接了日本东京日经225指数。这意味着原油变动所带来的风险可能经由印度传导至日本的股票市场。类似地，韩国综合指数不仅与原油相连接，还与中国上证综指以及英国富时100指数相连接，那么当韩国综合指数受原油影响时，相应的其他国家也会受到波及。不止于此，英国富时100指数还与其他欧美国家存在很强的正相依性，英国与法国国家指数，以及法国与德国国家指数之间的无条件秩相关系数均大于0.5。由此，风险进一步扩散，使得原油进口国的国家指数在一定程度上都受到油价波动的影响。

按照相同的步骤对原油及原油出口国的国家指数进行建模，并画出其第一层树结构图（图3）。如图3所示，与原油和原油进口国之间的风险传染路径一致，原油与原油出口国之间除了来自原油市场的风险溢出，原油出口国的国家股票市场之间也会形成一定的风险传染关系。在油价下跌期间原油与原油出口国国家指数间的相依结构中，不同序列之间的秩相关系数均为正，体现了原油以及原油出口国国家指数之间的正相依性。在该藤结构中，一个重要的节点是俄罗斯RTS指数。其与原油的秩相关系数为0.25，与挪威OBX指数和阿联酋DFM综合指数对应无条件秩相关系数分别是0.36和0.35。这是因为引起此次油价暴跌的一个重要的地缘政治因素是“乌克兰事件”。在欧美制裁以及油价暴跌的打压下以能源收入作为经济增长主要渠道的俄罗斯受到了一定的制约。此外，在该相依结构中阿联酋DFM综合指数又与沙特全股交易指数和尼日利亚综合指数相关联。沙特阿拉伯作为世界上最大的石油输出国，石油产业作为其主要经济支柱，但是在此次油价暴跌中沙特并没有首当其冲的受其影响，这是因为沙特拥有全球约四分之一的石油储备，同时掌握全球85%的石油闲置产能，且外汇储备量盘大，沙特完全能够接受更低的油价，打得起“价格战”。进一步观察其他原油出口国的相依结构，其中墨西哥与挪威的国家指数相连接，而加拿大又与墨西哥相关联。在此次油价暴跌中，加拿大以及沙特还有尼日利亚都处在了藤结构的边缘位置，受到的冲击相对较小。

图3 原油与原油出口国国家指数间的相依结构

总体上看，原油出口国国家指数与原油之间的相依程度相较于原油进口国国家指数会更高一些，其对应无条件秩相关系数更大。因为原油对于原油出口国来说是其经济产业的支柱，油价的变动对其带来的冲击更为显著。但是不管是原油进口国还是原油出口国，在油价剧烈变动时，一国股市的变动不一定是受能源市场的影响，更多的是受到其他国际股市的风险外溢。

三、结论

本文对国际原油市场以及15个依赖原油进出口的国家指数择优构建了R藤Copula模型，探究国际原油市场与国际股市之间的风险传染效应，得到以下结论。

首先，当国际原油市场作为风险源时，该能源市场在与原油进口国的相依结构中是一个节点，连接印度孟买Sensex指数和韩国综合指数，而在原油出口国的相依结构中则主要与俄罗斯RTS指数相连接。说明在该油价波动期间，最先受到影响的国际股市是印度、韩国和俄罗斯三个国家。其次，在油价暴跌期间，不同经济体股市之间反映出了不同程度的相依关系。这使得油价波动的影响进一步扩大，风险逐渐在不同经济体中扩散。最后，从整体上看，原油市场与原油出口国股市之间的秩相关系数较原油进口国更高，说明原油价格波动对原油出口国的冲击会更强一些。

本文借助R-Vine Copula模型对油价暴跌时期市场间的整体联动进行刻画，既有助于投资者及时判断市场走向，提高能源意识，还有助于各个国家及时防范能源风险和其他金融市场的风险外溢情况。

基于此，本文提出以下建议：一方面，对投资者而言，在密切关注金融市场的同时也要警惕能源市场风险，在能源市场发生异动时也要注意国际金融市场的联动。特别是在相依结构中与原油市场相连接的国际股市，要提前做好资产的风险管理预案。另一方面，对国家而言，在藤结构中与原油市场紧密相连的国家如俄罗斯等应注重调整国内产业结构，避免过度依赖资源发展而对其他经济活动造成影响。此外，藤结构中的其他国家在注重自身能源安全的同时也要注意防范外生性金融风险，避免受到其他国际股市带来的影响。