国际原油价格预测的研究动态与展望

□张跃军 邢丽敏

[湖南大学 长沙 410082]

引言

原油作为重要的能源产品，不仅具有一般的商品属性，还具有金融属性和政治属性，其价格波动对世界经济、金融市场和区域稳定具有显著影响[1～3]。根据《BP世界能源统计年鉴2020》数据，2019年石油消费仍占全球化石能源消费的首位，为33.1%[4]。同时，作为世界最大的发展中国家，中国经济过去几十年持续稳定增长，工业化进程不断加快，原油需求量也不断攀升。据BP统计[4]，自2015年以来，我国年石油消费连续位居世界首位，这导致我国原油对外依存度逐年上升，2020年已高达73.5%，如图1所示。

图1 2003～2020年中国原油进口量和对外依存度

原油需求过度依赖进口使得我国产生了巨大的外汇资金需求，同时，国际油价的频繁剧烈波动给我国原油进口成本和国内相关行业的经济效益造成了巨大不确定性。尽管2018年3月26日，我国原油期货的上市可以帮助企业通过期货交易降低国际油价波动风险，但石油企业在面临国际原油市场重大突发事件的冲击时仍然损失惨重。例如，2020年初突如其来的新冠肺炎疫情在全球蔓延，导致世界石油需求预期大幅降低，随后减产问题谈判破裂直接导致油价暴跌，并引发全球原油市场恐慌情绪蔓延。受疫情冲击，中国油气行业遭受大幅亏损，特别是上游开采行业[5]。例如，中石油集团2020年第二季度油气勘探生产业务的毛利率由上年同期的26.67%缩水为16.02%；而民营企业遭受的损失更加严重，如洲际油气企业的毛利率由上年同期的21.65%大幅跌至-4.96%。

为此，国际原油资产定价与预测成了我国能源供需安全甚至经济安全的核心关切。政府部门、企业和投资机构等都迫切希望能够对原油价格进行准确定价并对其走势进行预测，以开展科学的政策制定、生产投资和买卖交易等，同时最大程度地规避油价波动风险。

一、原油价格的主要影响因素

原油资产的复杂属性决定了国际原油市场是一个典型的复杂非线性系统，其价格波动是一系列风险因素相互交织、综合作用的结果。基本面和非基本面因素共同作用，导致国际油价发生剧烈波动，特别是2008年金融危机以来，世界经济疲软不振、原油市场供需平衡脆弱、投机基金不断游走以及地缘政治摩擦频繁，导致原油价格大起大落。国际原油市场最重要的两种基准油：西德克萨斯轻质（West Texas Intermediate，WTI）原油和布伦特（Brent）原油价格的变动趋势如图2所示。

图2 WTI和Brent原油价格走势

首先，原油作为重要的工业原料，具有一般商品的属性，其价格波动长期来看受供需基本面因素的影响。例如，2008年金融危机之前，国际石油市场供需基本平衡，全球经济的繁荣发展为油价上行提供了有力支撑[6]。而2008年金融危机后，原油市场供需格局发生了深刻变化，一方面全球经济复苏缓慢，另一方面美国页岩油产量增加，原油市场供需失衡，石油输出国组织（Organization of Petroleum Exporting Countries，OPEC）的减产措施成为支撑2009～2014上半年油价上涨的关键动力。同时，石油库存作为供需基本面的平衡器和调节器，不但影响石油市场供需变动，也会对市场投资者的预期产生影响，进而导致油价波动[7]。

其次，进入21世纪以来，随着全球金融市场不断演进，原油期货在国际大宗商品市场占据越来越突出的地位，原油的金融属性逐渐凸显，其价格波动受投机基金的影响也较为明显。原油期货市场的投资基金炒作叠加其他因素往往会对油价涨跌形成推波助澜的作用[8～9]。例如，2009年5～6月，全球经济持续复苏，美联储量化宽松导致美元弱势，加之OPEC产量保持低位，使投机者对油价的情绪回暖，资金持续流入能源板块，原油价格突破了70美元/桶，涨幅达36.5%。此外，由于原油价格以美元计价，美元指数的涨跌也会影响其价格变化。例如，2008年金融危机后美国连续实施四轮量化宽松政策，超低利率导致美元贬值，对这一阶段的油价上涨形成了重要支撑。

最后，由于石油资源的稀缺性，主要产油国长期以来对原油供应形成寡头垄断，产油大国之间的利益博弈以及地区冲突等地缘政治风险也对原油价格波动产生了不可忽视的政治化影响[10～11]。例如，2020年3月初的国际油价大跌，沙特和俄罗斯的博弈只是导火索，其背后则是国际能源格局变化的深层次问题。

原油市场的复杂系统特征及其引致的油价波动非线性、动态性等特征使得国内外学者多年来致力于探寻能够提高油价预测精度的方法。本文首先对目前油价预测的主要工作进行系统梳理，然后对油价预测的主要方法进行归纳总结，再给出未来油价预测有待拓展的方向。

二、油价预测研究综述

原油价格预测作为全球能源研究学者关注的重要议题，相关文章多发表于国际期刊上。因此，我们在全球广泛使用的论文数据库Web of Science中以关键词“crude oil price”“crude oil”“oil price”“forecast”和“predict”进行搜索，最终获取2002～2021年发表的295篇关于油价预测的学术论文。本文对这些油价预测论文进行系统梳理和剖析，发现目前油价预测方法主要包括三大类：计量方法、机器学习方法以及混合预测方法。

这些预测方法的主要区别在于：计量方法依据经济理论构建确定的估计方程，然后根据样本内参数估计进行样本外预测；机器学习方法直接对输入的样本数据进行不断学习和训练进而得到预测结果。两类方法各有优劣，运用计量模型可以有效识别影响原油价格的因素，所得预测结果可解释性更强；但是，由于模型设定形式的局限性及可能存在的设定偏误，其相比机器学习方法难以刻画油价波动的各种复杂非线性特征。而机器学习方法基于先进的人工智能算法，能够对油价序列的历史值进行反复学习和模拟训练，模型预测精度往往更高；但该类模型所得预测结果的可解释性较差，即仅通过对历史数据进行“黑箱”训练就得到预测结果令人难以信服，且机器学习算法容易陷入过度拟合和局部最优的陷阱。针对计量和机器学习方法各自的优劣，近几年的油价预测研究更倾向于同时运用计量和机器学习方法，即多种模型的综合集成运用。

对295篇油价预测的文章进行分析可知，采用计量方法预测油价的论文数量居多，合计180篇；机器学习方法次之，共93篇；而运用混合预测方法的论文有22篇。我们描绘出2002～2021年采用各类方法预测油价的文章发表趋势如图3所示。

图3 2002～2021年油价预测研究发表论文数量

可以发现，2002～2007年关于油价预测的论文发表数量寥寥无几。对相关文献进行阅读和分析发现，这一时期所用的预测方法以简单的计量模型（如普通最小二乘回归、自回归整合移动平均、向量自回归）和机器学习方法（如人工神经网络、支持向量机、遗传算法）为主。2008年金融危机发生后，油价预测的文章数量开始逐渐增多。具体而言，2007年有关油价预测的论文仅有1篇，而2008～2010年分别增加至6、13和11篇。这表明，金融危机导致原油价格大幅下跌，对全球经济社会的生产经营活动造成严重冲击，这使得广大学者意识到把握原油价格驱动因素、提高对油价走势的预测准确性是一项重要且紧迫的研究工作。2011～2013年，此时期油价预测的文章数量虽然有所减少，但机器学习方法在油价预测方面的应用却得到较快发展。2014年7月，由于原油市场供过于求，且全球经济疲软，加上OPEC拒不减产，直接导致WTI原油价格由90～100美元/桶的高位再次暴跌，此后原油价格开始长期低位震荡。原油价格的又一次大幅下跌吸引广大学者关注油价预测研究，且预测技术的不断改进使得自2014年开始油价预测文章的数量呈快速增长趋势。尤其是2018～2020年，油价预测研究工作呈现爆发式增长态势，各年发文数分别达到47、41和54篇。

接下来，我们对油价预测研究的发表期刊进行统计，主要发表期刊分布如图4所示。可以发现，油价预测的研究主要发表于《Energy Economics》《Energy》《Journal of Forecasting》《Economic Modelling》和《International Journal of Forecasting》等国际权威SCI/SSCI检索期刊，其中在能源经济领域的ABS三星级期刊（JCR分区一区）《Energy Economics》发文量最大，共计85篇。

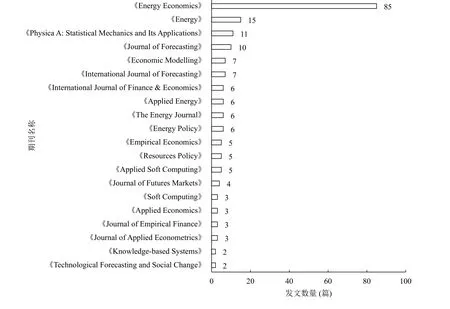
图4 2002～2021年油价预测文章发表期刊统计

进一步地，我们以期刊《Energy Economics》为例，对2018年发表于该刊的文章进行关键词分析，可以发现，在《Energy Economics》发表的论文中占比最高的关键词即为“oil price”，说明“油价”是《Energy Economics》期刊的关注热点。其他涉及原油市场预测的关键词还包括 “crude oil price”“volatility”“forecasting”“GARCH”“structure break”和“oil price shock”。从这些关键词可以看出，运用GARCH族模型对油价波动率进行预测十分热门，同时考虑原油价格的结构突变和油价冲击是油价预测的重点关注问题。

最后，我们对相关油价预测文章的作者单位进行统计，结果如图5所示。可以发现，中国学者是原油价格预测研究的最主要贡献者，其发文数量占油价预测总发文量的比重高达44%；其次是美国学者，其在油价预测领域发文数量占比为16.41%。就中国学者所在的研究机构而言，中国科学院数学与系统科学研究院在油价预测领域的发表文章数量为首位，为油价预测研究做出了突出贡献。其他在油价预测领域发文数量排名靠前的机构单位包括：西南交通大学、南京理工大学、北京化工大学、中国科学院大学、北京理工大学、西南财经大学、云南财经大学、湖南大学和南京审计大学等。

图5 发表油价预测文章的地域分布和研究结构统计

三、国际油价预测的主要方法

油价波动的影响因素错综复杂，且其波动的非线性、不确定性、动态性特征显著，因此，如何科学准确地对其价格变化进行预测是近二十年来国内外研究的热点。尤其是2008年金融危机以来，国际原油价格波动更加频繁，迫切需要开发出能够精确预测原油价格走势的模型方法。

现有关于原油价格预测的方法层出不穷，归结起来主要有两大类：一类是以普通最小二乘回归（Ordinary Least Squares，OLS）、随机游走（Random Walk，RW）[12]、不变模型（Nochange）[12]、自回归模型（Autoregressive，AR）、自回归整合移动平均（Autoregressive Integrated Moving Average，ARIMA）、向量自回归（Vector Autoregression，VAR）、向量误差修正模型（Vector Error Correct Model，VECM）等为代表的传统计量方法及其衍生预测模型。另一类是以人工神经网络（Artificial Neural Network，ANN）、支持向量机（Support Vector Machine，SVM）、最小二乘支持向量回归（Least Square Support Vector Regression，LSSVR）、遗传算法（Genetic Algorithm，GA）等为代表的机器学习方法及其拓展模型。近几年的研究逐渐开始结合计量和机器学习模型进行混合预测，以发掘各类方法的优势，获得更为精确的预测结果。事实上，对多个模型的综合集成运用确实往往可以获得比单种模型更好的预测效果。主要的国际油价预测方法总结如表1所示。

表1 国际油价的主要预测方法总结

（一）基于计量经济模型的国际油价预测研究

早期基于计量模型的油价预测研究，主要运用简单的ARIMA、VAR和VECM模型，且着重探究原油价格的有效预测变量。例如，Ye等[13～14]利用传统的OLS回归模型预测油价，证实了OECD石油库存对油价预测的重要作用。Coppola[15]利用VECM模型考察了原油期货价格对原油现货价格的长期均衡关系，发现原油期货市场的信息可以解释部分原油价格的变化。Murat和Tokat[16]同样基于VECM模型，发现原油与石油产品的基差对原油现货价格具有短期和长期影响，而且利用基差变量所得的油价预测结果优于基准的RW模型。

1.原油价格收益率预测方法

在相关研究中，学者们提出各种策略以提高计量模型对油价收益率的预测能力，如运用实时数据（Real-time Dataset）、对参数估计施加约束、对估计结果进行组合加权以及连续筛选预测变量等。例如，Baumeister和Kilian[17]提出利用实时数据预测油价收益率，发现运用实时数据可以提高VAR等计量模型对美国炼油商的进口收购成本的预测精度，其预测误差和预测方向正确性率不仅高于基准的RW模型，且高于AR和ARIMA模型。在施加约束方面，Wang等[18]提出对参数估计施加经济和统计意义层面的约束来预测原油价格，发现通过舍弃参数估计符号与其经济意义不符以及样本内统计不显著的变量，可以提高OLS模型的预测精度。随后，Yi等[19]通过对预测变量、系数符号和回归结果施加组合约束，发现相比单一的约束方式，组合约束可以显著提高油价预测精度。

考虑到模型设定的不确定性，单一模型的预测效果可能不会一直表现很好，Baumeister和Kilian[20]提出组合预测的思想来预测油价收益率。组合预测是将单一模型的预测结果基于不同权重进行加权组合，结果表明组合预测确实可以提高油价的样本外预测精度。在Baumeister和Kilian的基础上，Wang等[21]提出运用时变参数的OLS回归对油价收益率进行预测，然后采用多种权重估计方法对单一模型的预测结果进行加权平均，即TVP-FC方法，结果发现TVP-FC预测结果不仅好于单一模型的预测结果，且优于基于固定系数模型的组合预测结果。Zhang等[22]采用一种新的组合预测方法，即迭代组合方法预测油价收益率，发现新的组合预测方法好于传统的组合预测方法。其他的组合预测方法还包括动态模型平均（Dynamic Model Average，DMA）[23～24]等。

与组合预测方法不同，收缩模型通过对影响原油价格的驱动因素进行动态筛选，可以剔除冗余变量，有效识别出最主要的预测变量，从而提高对原油价格的预测精度。例如，Ma等[25]基于多种预测指标，包括宏观经济变量、技术变量和情绪类变量，运用收缩方法即最小绝对收缩和选择算子（Least Absolute Shrinkage and Selection Operator，LASSO）回归，以及组合预测方法（DMA和TVPFC）预测油价收益率，结果表明LASSO回归的预测效果相对更优。Zhang等[26]运用收缩方法（LASSO、弹性网络）和其他竞争模型（如DMA、组合预测、偏最小二乘回归、主成分分析）预测油价收益率，结果表明用收缩方法的预测效果好于其他模型。考虑到原油市场经常发生剧烈波动，油价序列的不稳定性可能对造成参数估计的较大偏差，Hao等[27]采用基于Huber损失函数的收缩方法预测油价收益率，结果表明该方法所得预测结果不仅优于基于OLS估计的单一模型和组合预测，也优于原始收缩方法。

鉴于预测变量数据频率的差异性，有学者发现利用高频数据能够提高对低频原油价格的预测精度。例如，Baumeister等[28]基于周度和日度金融数据，利用混频数据模型（Mixed Frequency Data Sampling，MIDAS）和混频VAR模型（Mixed-Frequency Vector Autoregressive，MF-VAR）预测月度WTI原油价格，结果表明高频金融数据的确有利于提高模型预测精度。Zhang和Wang[29]综合运用MIDAS回归、基于自回归分布滞后（Autoregressive Distribution Lags，ADL）的ADL-MIDAS模型和MF-VAR模型，发现ADL-MIDAS模型的预测效果最好，其次是MIDAS，而MF-VAR模型的表现不如前两者。

2.原油价格波动率预测方法

油价波动率对于计算风险价值和投资者进行风险管理具有重要意义，因此有大量研究聚焦油价波动率预测。广义自回归条件异方差（Generalized Autoregressive Conditional Heteroscedasticity，GARCH）族模型由于能够捕获油价变化的长短记忆特征，被广泛运用并不断改进。

从现有研究成果来看，尚未有预测效果绝对最优的单一机制GARCH族模型。Morana[30]首次尝试将GARCH模型用于预测Brent油价波动率，证实了该方法对原油价格波动率的可预测性。Cheong[31]发现捕获短记忆特征的GARCH模型在预测Brent油价波动率方面具有良好性能，而能够捕获长记忆特征的分数单整（Fractionally Integrated）的FIGARCH和分数单整非对称幂（Fractionally Integrated Asymmetric Power）的FIAPARCH模型对WTI油价波动率的预测效果更好。Kang等[32]发现FIGARCH模型对Brent油价波动率的样本外预测效果更好，而能够同时捕获长短记忆特征的成分GARCH（Component GARCH, CGARCH）模型对WTI油价波动率的预测性能更好。Wei等[33]纳入八种线性和非线性GARCH族模型对WTI油价波动率进行预测，发现非线性GARCH族模型的长期预测精度高于线性GARCH族模型。

相比单一状态的GARCH族模型，马尔科夫机制转换（Markov Regime Switching，MRS）GARCH族模型由于能够捕获油价波动的不同状态也被广泛应用。例如，Fong等[34]采用马尔科夫过程刻画油价波动的机制转换特征，结果表明MRSGARCH模型的预测效果显著优于单一状态的GARCH模型。Xu和Ouenniche[35]的研究也表明考虑机制转换特征的MRS-EGARCH模型对油价收益率、波动率和风险价值的样本外预测误差均小于一般的EGARCH模型。Klein和Walther[36]采用基于混合记忆（Mixture Memory，MM）的MM-GARCH模型刻画油价波动的不同状态，发现MM-GARCH模型的预测能力好于单一机制的GARCH族模型。Lin等[37]基于隐马尔科夫（Hidden Markov，HM）的HM-GARCH模型预测油价波动率，发现该模型预测效果好于单独的GARCH族模型和MRSGARCH模型。然而，Zhang等[38]研究发现，考虑机制转换的GARCH模型（包括MRS-GARCH和MMGARCH）的样本内拟合效果虽然很好，但其样本外预测效果并不优于单一机制的GARCH族模型。综上所述，大量相关研究并没有对哪种GARCH模型的预测效果最好达成一致结论，这可能与样本区间、预测长度、参数设置等问题有关。另外，还有学者发现马尔科夫转换多重分形（Markov Switching Multifractal，MSM）模型对油价波动率的预测效果优于传统的GARCH族模型[39～40]。

上述研究中的GARCH族模型往往基于日度数据，且以收益率的平方表示波动率，难以体现更高频的交易数据信息。自从已实现波动率异质自回归模型（Heterogeneous Autoregressive Model-Realized Volatility，HAR-RV）模型被提出以来[41]，分钟高频数据在能源金融市场的研究中得到广泛应用，且大量研究表明利用高频数据构造的低频RV值能够捕获油价波动的长记忆性，所得油价波动率预测结果精度往往更高。Liu和Wan[42]使用日内分钟高频数据构造已实现波动率预测上海燃料油期货价格波动率，结果表明基于能够表征长记忆性和波动持续性的自回归分数单整移动平均（Autoregressive Fractionally Integrated Moving Average，ARFIMA）模型对已实现波动率的预测精度远高于Wei[33]等采用的GARCH族模型。此后，HAR-RV族模型被广泛应用并得到持续改进，且研究结果大多表明考虑日内高频数据信息能够提高对油价波动率的预测精度。

例如，Wen等[43]将结构突变引入HAR-RV族模型预测原油期货的已实现波动率，发现引入结构突变的HAR-RV族模型预测效果较简单的HAR-RV模型预测效果更好。其中，考虑连续样本路径方差和离散跳跃方差的HAR-CJ模型在预测未来一天和一个月时效果最好，引入正负已实现半变差的HARRSV模型对未来一周油价波动率的预测效果最好。Ma等[44]将油价波动的机制转换特征引入HAR-RV族模型，发现相比单机制的HAR-RV族模型，虑机制转换特征的MRS-HAR-RV族模型的样本外预测精度更高。Zhang等[45]将收缩预测和组合预测方法引入HAR族模型，对油价波动率进行预测，发现基于两种收缩方法（即弹性网络和LASSO回归）所得的样本外预测结果不仅好于单一的HAR-RV族模型，而且好于基于组合预测方法的HAR-RV族模型。Chen等[46]将HAR-RV模型与FIGARCH模型相结合，结果表明相较线性HAR-RV模型，考虑油价波动ARCH效应的HAR-RV族模型预测精度更高。Luo等[47]将无限状态的隐马尔科夫模型（Infinite Hidden Markov，IHM）引入HAR族模型，发现IHM-HAR模型的预测效果好于没有考虑机制转换的HAR族模型。

另外，还有学者考察了外生变量对HAR模型预测油价波动率的影响，如投资者情绪、原油市场隐含波动率指数、股票市场和其他期货市场的已实现波动率[48～50]。但是，也有部分学者发现HAR-RV模型的样本外预测精度并不比低频GARCH族模型更好。例如，Sévi等[51]利用HAR模型预测WTI原油期货的已实现波动率，发现考虑跳点和半方差的HAR-RV模型的样本内拟合精度相比GARCH族模型有所提高，但对提高样本外预测精度无益。

（二）基于机器学习方法的国际油价预测研究

机器学习是预测国际油价的另一类重要方法，且各种前沿算法被不断用于油价预测，使得预测结果精度持续提高。早期相关研究主要利用神经网络模型或支持向量机方法预测油价，研究结果发现这类非线性模型的预测性能往往好于传统的线性模型（如ARIMA、VAR模型等）。

在利用传统的机器学习方法预测油价方面，Kaboudan[52]使用ANN和GA模型预测油价，发现GA相比基准的RW模型可以获得更好的预测结果，而ANN的预测结果却不如RW模型。Mirmirani和Li[53]将基于GA算法的反向传播神经网络（Back-Propagation Neural Network，BPNN）模型和VAR模型所得油价的预测结果进行对比，发现前者的预测结果显著好于后者。Wang等[54]提出了一种改进的混合人工智能系统框架，即将ANN、基于规则的专家系统和基于网页的文本挖掘技术相结合，发现该混合方法能够显著提高原油价格预测精度。Xie等[55]提出使用SVM方法预测油价，发现该模型的预测性能优于ARIMA和BPNN模型。Moshiri和Foroutan[56]将ANN模型的预测结果与GARCH模型、ARIMA模型相比，发现ANN模型对原油价格的预测性能更优。

1.分解集成预测方法

根据Wang等[54]的TEI@I预测思想，Zhang等[57]将集成经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）技术用于分解具有非线性和非稳定特征的原油价格序列。自此，分解–集成预测方法被广泛应用于油价预测领域，且获得了良好的预测效果。常见的分解技术包括EMD、EEMD、小波分析（Wavelet Analysis，WA）、奇异谱分析（Singular Spectrum Analysis，SSA）、变分模态分解（Variational Mode Decomposition，VMD）等。针对EMD和EEMD在恢复信号的过程中引入新的噪声和“模态混合”等问题，VMD方法对其进行改进并被广泛应用。

已有研究表明，结合分解方法和ANN或SVM模型确实可提高单一机器学习模型的预测精度。例如，Yu等[58]提出利用EMD方法将油价序列分解为几个固有模态函数（Intrinsic Mode Functions，IMFs），然后利用前馈神经网络模型分别对IMFs进行预测，最后应用自适应线性神经网络模型集成多个IMFs的预测结果，证实了分解–集成方法预测性能优于单一的神经网络模型。类似地，杨云飞等[59]结合EMD和SVM模型对原油价格进行预测。Wang和Li[60]将SSA和BPNN模型结合预测大宗商品价格（包括原油价格），证实了该混合模型的预测优越性。Jammazi和Aloui[61]将小波分解技术和多层BPNN神经网络模型结合，结果表明该方法的预测性能好于单一的BPNN模型。

近几年的相关研究中，预测效果更好的机器学习模型或更优的预测策略被应用于分解–集成预测研究中。例如，Tang等[62]提出运用互补集成经验模态分解（Complementary EEMD）方法得到原油价格序列的多个IMFs，然后运用扩展的极限学习机（Extended Extreme Learning Machine，EELM）方法预测各IMFs，最后将各子序列的预测结果相加得到最终的预测值，该模型被证实可以有效提高原油价格的预测精度，且EELM算法的预测效果好于基于其他算法的神经网络模型。Yu等[63]同样结合EEMD分解方法和EELM算法，证实了该方法在预测油价方面的优越性。Wang等[64]分别将EMD、VMD、WA、SSA四种分解方法与AR、ARIMA、ANN和SVM模型相结合，共得到16种组合预测模型，结果表明组合预测较单一模型能够大幅降低预测误差。Tang等[65]提出将EEMD方法和基于随机向量函数链（Random Vector Functional Link，RVFL）算法的神经网络模型用于油价预测，结果表明EEMD-RVFL模型的预测精度不仅高于单独ELM网络模型、核岭回归、随机森林、BNN、LSSVR、ARIMA模型，且好于EEMD和这些模型的组合预测结果。Bisoi等[66]将VMD与RVFL神经网络模型相结合，证实了该方法的代码运行时间和预测误差均小于VMD和BPNN、ARIMA、LSSVR、自适应神经模糊推理系统（Adaptive Neuro-fuzzy Inference System，ANFIS）、区间二型模糊神经网络和递归神经网络（Recurrent Neural Network，RNN）的组合。张金良等[67]基于VMD和果蝇算法优化后的最小二成支持向量机（Least Squares SVM，LSSVM）构建了混合预测模型，并证实了该预测方法对油价具有良好预测性能。Yu等[68]从集成策略的多样性角度出发，综合分析了样本数量多样性、抽样区间多样性、参数设置多样性、集成数量多样性和集成方法多样性这五种不同策略对RVFL神经网络模型预测性能的影响。结果表明，考虑多种策略组合的RVFL集成模型预测精度相比单一的RVFL模型预测精度有显著提高。唐振鹏等[69]基于VMD和EEMD相融合的二次分解技术，结合差分进化（Differential Evolution，DE）算法优化后的极限学习机（Extreme Learning Machine，ELM），提出对原油价格的VMD-RES-EEMD-DE-ELM混合多步预测模型，实证结果表明，与其他的基准模型相比，作者提出的混合模型有效且稳健。

2.深度学习预测方法

深度学习是机器学习研究中的一个新领域，其能够通过构建包含很多隐含层的机器学习模型对海量数据进行训练，表征数据分布特征，从而提升对复杂文本、声音、图像等数据的分类或预测的准确性。目前原油市场预测中常用的深度学习模型包括长短期记忆网络（Long Short Term Memory Network，LSTM）、门控循环单元（Gated Recurrent Units，GRU）、卷积神经网络（Convolutional Neural Networks，CNN）和深度置信网络（Deep Belief Networks，DBN）、去噪自编码机（Denoising Autoencoders，DAE）。其中，LSTM网络是一种改进的RNN模型，其通过引入门单元能够学习时间序列的长期依赖信息，对于具有显著序列相关性的经济金融数据具有较强预测优势。GRU和LSTM的网络结构类似，也包括门单元，但是GRU设置的门单元数量更少，模型训练所需参数少，训练难度较小且易收敛。

近年来，深度学习逐渐被应用于原油市场研究，且部分研究表明深度学习模型在原油市场预测中能够获得更优的结果。Chen等[70]将DBN和LSTM与线性模型（RW、ARIMA）相结合，结果发现深度学习模型有助于提高原始模型对油价的预测精度。Zhao等[71]将堆叠去噪自编码机（Stacked Denoising Autoencoders，SDAE）用于刻画原油价格与其影响因素间的非线性复杂关系，并运用自助聚合算法训练样本抽样以提高SDAE模型的预测精度，结果表明该方法可以大幅提高对原油价格的预测准确性。Wu等[72]将EEMD分解方法和LSTM相结合预测国际油价，发现该方法的预测表现优于EEMD和ELM、LSSVR、ANN、ARIMA的结合的预测结果。Huang和Deng[73]将改进的信号–能量（Improved Signal Energy，ISE）规则用于VMD分解方法的参数选择，然后运用移动窗口（Moving Window，MW）策略作为VMD分解的补充，提出了VMD-LSTM- MW预测方法对原油价格进行日度和月度预测，实证结果证实了该方法的优越性。Wang和Wang[74]基于随机遗传公式（Random Inheritance Formula，RIF）和门控循环单元模型，提出RIF-BiGRU模型预测国际油价，并将预测结果和SVM、LSTM、GRU以及RIF-GRU模型做比较，结果表明RIF-BiGRU的预测精度高于其他模型。Li等[75]基于文本数据构建了投资者情绪指数，先运用VMD模型分解油价序列，然后运用双向BiLSTM模型对原油价格收益率和波动率进行预测，结果证实VMD-BiLSTM模型相比其他竞争模型具有优越的预测性能。

基于卷积核和反向传播过程，CNN在文本数据特征提取和情感分类方面具有巨大优势。例如，Li等[76]采用CNN方法对原油市场相关新闻进行特征提取，然后基于潜在狄利克雷分布主题模型对情感特征进行聚合从而构建情绪指数，实证结果表明，采用CNN算法构建情绪指数对提高油价预测结果有显著作用。Wu等[77]首先运用CNN模型提取石油市场新闻的特征信息，然后利用VMD方法剔除新闻数据中的无用信息，进而构建基于文本数据的原油市场情绪指标，最后运用多种模型，如多元线性回归、BPNN、SVM、RNN、LSTM和GRU预测原油价格，证实了新闻数据对预测原油价格的重要作用。

（三）基于混合方法的国际油价预测研究

现有多数研究主要基于单一的计量模型或机器学习方法预测油价收益率或波动率，实际上将两类预测方法相结合往往可以获得更好的预测结果。

例如，Ou和Wang[78]认为神经网络能够克服传统计量模型在参数估计中由于各种先验假设所导致的估计偏误，由此构建了GARCH-ANN模型，结果表明该模型在不同参数设定情况下的预测结果均显著优于GARCH模型。Bildirici和Ersin[79]分别运用平滑转换自回归（Smooth Transition Autoregressive，STAR）和多层感知机（Multi-Layer Perceptron，MLP）神经网络刻画GARCH族模型条件均值和条件方差的非线性，发现新方法的样本外预测结果远好于原始的GARCH族模型。Zhang等[80]首先运用EEMD分解原油价格序列，然后分别用GARCH模型和基于粒子群优化的LSSVM模型刻画油价波动率序列的时变性和非线性特征，最后合成各IMFs序列的预测结果。结果证实，混合预测方法的表现远好于其他竞争模型。Safari和Davallou[81]分别运用线性模型（指数平滑法和ARIMA）以及非线性模型（非线性自回归神经网络）预测原油价格，并根据卡尔曼滤波算法和状态空间模型计算出时变组合权重，发现基于该时变权重所得的预测结果好于基于等权重、遗传算法求解权重所得的预测效果。Zhang等[82]首先运用HMM识别出原油价格波动的不同状态，然后分别采用EGARCH和LSSVM预测原油价波动率和残差序列，并运用误差修正模型（Error Correct Model，ECM）模型不断修正预测结果，最终的预测结果表明，新的混合模型预测性能较其他相关模型更优。Abdollahi和Ebrahimi[83]分别利用ANFIS、ARFIMA和MRS模型预测原油价格，并基于不同权重得到各模型的加权平均预测结果，然后运用GA算法对各模型预测结果进行加权，所得的最终结果显著好于基于等权重和预测误差最小加权的方法。

四、研究评述与展望

（一）研究评述

本文通过对油价预测领域的相关文献进行系统总结和梳理，发现国内外学者主要基于计量和机器学习方法进行国际油价预测研究，也有部分研究将计量和机器学习方法相结合，以提取原油价格序列的复杂变化特征，获得更为精确的预测结果。根据已有研究，本文认为油价预测领域还存在一些亟待研究的问题：

1.缺乏对超高频数据预测作用的研究。随着金融市场的快速发展，交易频率大大加快，借助现代金融信息技术，可以收集到时间间隔很小的高频交易数据，比如每一分钟交易数据，甚至每一笔交易数据。相比日度数据，高频数据包含了更多的交易信息，研究者可以在更高的数据频率下探究资产价格变化规律，研究其对资产价格的预测作用。然而，目前较少有研究涉及高频交易数据对油价的预测作用。虽然HAR-RV族模型运用了高频分钟数据，但经过线性变化其高频数据信息仍被包含在低频变量内，估计模型仍采用日度数据进行预测。因此，有必要探索适合高频数据估计的模型方法。

2.缺乏对原油价格区间预测和概率密度预测开展研究。区间预测和密度预测均属于不确定预测，即给出未来资产价格的变化范围和出现某个预测值的概率大小。然而，现有油价预测研究多为点预测，即预测未来时刻油价的期望值，缺乏对区间和概率密度预测的研究。实际上，把握原油价格的精确变化几乎是不可能的，虽然各种前沿计量模型和机器学习方法能够在很高的预测精度下给出油价变化的确切值，但是政策制定者和市场参与者可能更关注价格的变化区间或未来资产价格在多大概率水平下上涨或下跌。因此，有必要深入对原油价格区间和概率密度预测的研究。

3.对计量与机器学习预测方法的结合探索不足。根据前文综述，目前针对油价预测领域的计量和机器学习方法探究均实现了跨越式发展。然而，两类预测方法的演进过程实际上是并行独立的，缺乏对两类预测方法交互融合后预测效应的研究。有必要尝试将前沿的计量方法（如组合预测、收缩模型）和深度学习模型（如LSTM和GRU）相结合，以发掘各类方法的优势，获得更优的预测效果。

4.预测结果的应用研究需要进一步丰富。尽管油价预测结果在风险管理和投资组合的应用研究方面取得了一些进展，但是目前大部分油价预测的研究仅局限于预测结果在统计意义层面的比较，缺乏对预测结果经济应用价值的深层次挖掘，缺乏与相关市场主体就预测结果的实际应用进行深入沟通探讨。

（二）研究展望

基于油价预测领域存在的问题和挑战，本文提出一些该领域未来可能的研究方向：

1.考察高频数据对油价预测的作用。信息技术的快速发展产生了有别于传统数据的新型数据，如函数型数据[84]。函数型数据的观测频率极高几乎可认为是连续数据，对该类型数据进行分析可采用函数型数据分析（Functional Data Analysis，FDA）方法，其假设资产价格具有某种函数特性。利用函数型数据，可以预测下一个原油期货价格变动的时点、未来每个时间点原油价格变动的概率，此类研究可改善投资机构的交易策略和风险管理水平。已有研究表明利用FDA方法从股票高频数据中提取主成分，能够显著提高基本的AR模型对股票价格的预测能力[85～86]。总之，高频交易数据包含了价格变动更为丰富的信息，所得预测结果可用于量化投资交易策略设计和衍生品定价，未来研究需要开发出新的适合高频数据建模的计量和机器学习方法。

2.探索原油价格区间预测和概率密度预测的理论方法。一方面，原油价格区间数据包含了最高价和最低价等信息，对油价变化进行区间预测对于政策制定者和市场参与者把握价格运行区间，防范化解风险意义重大；另一方面，相较于传统的点预测，概率密度预测不仅可以得到未来某时刻油价的期望值，还可以获取其概率分布信息，即该时刻下所有可能的油价值及其出现的概率，可为决策者进行政策制定、调整投资决策提供全面参考。现有理论与方法在应用于区间数据分析时并不完全适用，需要发展适合区间数据的理论和方法，并提出适合评估区间预测和概率密度预测结果准确性的指标[87]。

3.将计量方法和机器学习预测方法有机结合。未来研究有待将两类预测方法的优势深入融合，以获得更好的预测效果。例如，鉴于单一模型不太可能始终获取最优的预测结果，即存在模型不确定性，可将计量领域的组合预测思想用于机器学习方法中；运用多种神经网络和深度学习模型获得多组油价预测结果，然后将各预测结果基于不同权重计算方法加权平均；运用LASSO等变量筛选方法选取各时期影响油价变动的主要变量，把握各时期影响油价变动的主要驱动因素，并基于各预测变量利用机器学习方法预测油价，以增强机器学习预测结果的可解释性。

4.深化预测结果的应用价值。扩展预测结果的实际应用价值值得研究学者在未来研究中深入探究，广大学者可加强和相关政府部门、企业和投资机构的合作，以使学术成果更好服务实体决策。例如，原油价格预测结果如何为我国石油储备中心调整进出口额度等提供决策支持？如何为石油相关企业调整生产经营策略提供参考？如何为原油期货市场参与者进行套期保值等业务提供交易策略指导？这些问题都值得广大学者未来进一步探究。