基于相关度距离的无监督并行哈希图像检索

杨 粟，欧阳智，杜逆索

（1.贵州省公共大数据重点实验室（贵州大学），贵阳 550025；2.贵州大学计算机科学与技术学院，贵阳 550025）

0 引言

基于内容的图像检索（Content Based Image Retrieval，CBIR）［1］是根据输入的查询图像，以图像语义特征为线索从图像数据库中检索出具有相似特性的其他图像。CBIR 主要利用图像视觉特征向量直接进行检索，通过计算图像特征向量之间的距离判定图像相似度，返回图像检索结果。在大规模图像检索领域，用近似最近邻搜索算法能提高检索速度，减少开销［2］。对于给定的一幅查询图像，传统的线性查找需要从庞大的数据库里快速找出相似图像，过于费时费力。K-D 树（K-Dimensional Tree，KD Tree）等［3］通过分割K维数据空间的优化算法并没有过多提高高维空间里的搜索效率，其效率甚至低于线性扫描，导致难以直接用于实际问题。近似最近邻搜索则在满足一定距离范围要求就能检索到高度相似的数据，帮助人们在海量数据中快速搜索到有效内容，因此在解决实际问题特别是图像检索领域受到广泛应用和研究。

哈希算法［4］是近似最近邻搜索中最为通用的算法之一。哈希算法在图像检索中将图像表示成一串紧凑的二进制码，使得相似的图像具有相似的二值码，即汉明距离尽可能小。图像哈希通过对高维的特征矢量进行哈希学习得到低维的二进制哈希编码，能够极大地降低计算及存储消耗。基于哈希的算法在图像检索中缓解了维数灾难，降低了图像检索系统对计算机内存空间的要求。

基于图像的哈希算法可分为监督、半监督、无监督三类，代表模型分别有Liu 等［5］提出的核监督哈希（Kernel Supervised Hash，KSH），Shao 等［6］提出的稀疏谱散列（Sparse Spectral Hashing，SSH），Zhu 等［7］提出的语义辅助视觉哈希（Semantic Assisted Visual Hashing，SAVH）等。目前，大部分工作主要还是围绕于有监督的图像哈希学习，然而，在实际应用中，获得高质量的标签信息需要付出大量的成本和人力代价［8］。

针对于更广泛的、无标记的数据，无监督的哈希方法受到更多关注。无监督方法中为了得到数据点之间的联系，通常使用余弦距离（如Deng 等［9］提出的语义对抗哈希（Semantic Preserving Adversarial Hash，SPAH））或欧氏距离（如王伯伟等［10］提出的语义相似度哈希）来计算特征相关性。余弦距离是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异大小的度量，但对具体数值不敏感，无法衡量每个维数值的差异。欧氏距离将样本的不同属性（即各指标或各变量量纲）之间的差别等同看待，使得每个坐标对欧氏距离的贡献是同等的，所得结果并不能完全符合现实中向量各分量的度量标准不一样的情况。因此，距离计算方式对实际检索中获取精确的语义信息有重要的影响。

另一方面，当哈希编码长度发生变化时，模型的再训练往往是不可避免的，这导致了过多的时间开销和哈希码信息冗余。例如Heo等［11］基于超球面分割数据点所提出的球面哈希（Spherical Hash，SpH）能够提高检索速度和准确性，但改变哈希码长度则要重新训练。因此，无监督哈希图像检索中语义信息未得到较好学习和需要多次训练的问题仍未得到良好解决。

针对上述问题，本文提出了基于相关度距离的无监督深度并行哈希图像检索模型。首先，通过利用卷积神经网络（Convolutional Neural Network，CNN）学习图像特征，使用相关度距离计算特征距离构造伪标签指导整个训练过程，通过与传统的余弦距离、欧氏距离比较，探讨特征距离对检索精度的影响；然后在传统卷积网络中嵌入多个哈希层得到不同码长的二进制码并相互关联，基于所提出的并行检索模式，一次生成多种长度的哈希码，并通过与传统单次训练模式比较，分析其对训练时间的影响。通过引入相关度距离提高图像检索的精度，同时利用并行模式来减少训练时间，以此对无标签的大规模图像检索提供一定的参考。

本文主要工作如下：

1）在无监督深度哈希图像检索中采用了相关度距离计算数据点之间的距离，与以往方法相比能较好地拟合数据间的分布，捕捉到更加接近真实的语义信息，实验结果表明，该方法能有效提升检索精度；

2）提出了一种无监督哈希并行模式，大量减少了目前已有模型中由于转换哈希码长度带来的时间开销，同时缓解了哈希码独立训练没有信息交互产生冗余的问题。

1 相关工作

监督哈希算法要求数据库中的全部数据都加上标签，每个样本对应的类别标签作为ground-truth 来训练网络，从而得到哈希函数。例如Xia 等［12］提出的卷积神经网络哈希（Convolutional Neural Network Hash，CNNH）包括了两个阶段来学习图像表示和哈希码：第一阶段是哈希函数学习，利用监督信息得到哈希编码；第二阶段是特征学习，训练深度卷积神经网络，用于将输入映射到第一阶段学习的哈希编码上，使模型可以同时学习到图像的特征表达以及哈希函数。Gionis等［13］提出的二进制重建嵌入（Binary Reconstruction Embedding，BRE）通过明确的最小化原始距离和汉明空间中重构距离之间的误差来学习哈希函数。Shen 等［14］提出的监督离散哈希（Supervised Discrete Hash，SDH）使用监督信息和离散循环坐标下降法直接优化二进制哈希码。这些模型将深度学习与哈希编码结合，能有效利用监督信息生成精确的哈希码，但是对于大量未标记的数据，如何衡量图像间的相似程度并进行训练成为了新的难点。

针对丰富的未标记数据，基于哈希函数的无监督学习算法通常需要保持原始空间中训练数据点的重要性质，通过利用距离函数学习数据中潜在的语义关系对模型进行训练。例如，Deng 等［9］提出的SPAH 首先提取深度特征，然后根据不同图像对的余弦距离进行k 近邻搜索，得到初始相似矩阵；将这种语义相似度矩阵的监控集成到对抗性学习框架中，可以有效地保存汉明空间中训练数据的语义信息。林计文等［15］提出的深度伪标签无监督哈希（Deep Pseudo-label Unsupervised Hash，DPUH）在处理无标签情况时对图像特征使用余弦进行统计分析，用于构造数据的语义相似性标签，再进行基于成对标签的有监督哈希学习。Song 等［16］提出的（Binary Generative Adversarial Network，BGAN）通过将生成对抗网络（Generative Adversarial Network，GAN）［17］的输入噪声限制为二进制，并根据每个输入图像的特征进行约束；在标签获取方面使用特征向量的余弦相似性来比较图像，从而获取最终的邻域结构指导学习。另一方面，王伯伟等［10］提出的语义相似度哈希首先则通过欧氏距离来构造一个语义相似度矩阵，然后在目标函数中加入范数，使得具有相同语义的图像具有相似哈希码。王妙等［18］采用由粗到精的分级策略，先根据学习到的哈希码使用汉明距离得到图像池，然后对计算池内图像高层语义特征之间的欧氏距离进行精检索，从而找到最相似图像。但是，使用这些距离度量得到的伪标签由于计算方式的限制并没有更好地捕捉到数据之间的语义相关性。针对此问题，在其他领域，魏永超［19］提出的基于相关数与相关距离的证据合成方法中使用了相关度距离计算证据向量距离，该距离主要通过相关系数来衡量两个向量的线性相关程度，能很好地拟合数据间分布，因此在证据合成中表现良好。

另一方面，目前的哈希模型在获得不同哈希码过程中都不可避免地需要多次训练。例如，Cao 等［20］提出的（Hash with Pair Conditional Wasserstein GAN，HashGan）中哈希码长度作为一个参数被预先指定，每换一次长度都需要重新指定再次训练。这种现象在哈希检索模型中广泛存在，包括文献［9-10，16，18］等，这往往导致较多的时间开销和哈希码信息冗余。针对模型多次训练的问题，一些学者在其他近似最近邻算法中提出了一些解决思路。例如Gao［21］等、Song 等［22］分别提出了深度递归量化（Deep Recurrent Quantization，DRQ）和深度渐进量化（Deep Progressive Quantization，DPQ），这两种模型都是依次获得二进制码并逐步逼近原始特征空间，可以同时训练不同码长的二进制码；但这两种模型都是基于量化的近似最近邻搜索方法，且仍需要利用标签信息来指导视觉特征的学习，没有考虑无监督环境下不同哈希码之间的内在联系。

综上所述，本文主要针对无监督哈希图像检索中语义信息学习不够，哈希码长度每换一次就要重新训练模型的问题，提出了基于相关度距离的无监督并行哈希图像检索模型。本文虽然与大多数无监督方法一样需要构建伪标签，但区别于传统方法中使用的欧氏距离或者余弦距离，本文采用的相关度距离能更好地捕捉语义信息，通过相关度距离直方图设置阈值构建出接近真实的相似矩阵；另一方面，不同于传统方法中更改一次哈希码长度就需重新训练，本文提出一种并行哈希模式，只需训练一次就可得到不同长度哈希码，大量减少了检索时间。最后，通过实验验证了本文所提出的模型在减少训练时间和提升哈希图像检索准确率上具有重要意义。

2 无监督哈希图像检索

2.1 符号与问题定义

在有N张图像训练集X=中，xi表示第i张图像。哈希算法的目标是将这些高维图像通过哈希函数F映射到低维的汉明空间生 成K位的哈希码，即F：X→B，B∈{1，-1}N×K。该哈希函数要求在原始空间中的相似图像在汉明空间中距离较近，在原始空间中不相似的图像在汉明空间中距离较远。假设Z为图像的连续特征，其表示为Z∈RN×K，然后通过将特征Z量化为二进制哈希码。哈希算法目标是学习图像的二进制哈希码B和可用于生成哈希码的哈希函数F。

2.2 模型框架

本文模型的结构框架如图1 所示，该框架由两个主要部分组成：1）无监督特征提取组件，用于伪标签矩阵构造；2）深度并行哈希学习，用于将特征转换为二进制码。本文使用CNN 中的VGG16［23］作为基础模型，通过改进基础模型来对特征和哈希码进行学习。原始的VGG16 模型包含5 个卷积层（Conv1～Conv5）和3 个完全连接层（FC6～FC8），该模型在计算机视觉中的图像检索和目标检测领域表现出了较好的精准率和召回率［24-25］。本文首先对VGG16 模型进行一定的调整，然后在FC7 层后加入4 个哈希层，构造伪标签矩阵进行无监督语义学习，最后通过损失函数进行联合学习，实现同时训练获得不同长度哈希码。

图1 本文模型框架Fig.1 Framework of the proposed model

2.2.1 基于相关度距离的无监督语义学习

无监督语义学习是为了分析数据点之间的语义关系，学习通过卷积神经网络获得的图像深度特征，进而捕捉不同图像间的内在视觉联系。通过训练未标记的数据将其编码为二进制代码，在编码过程中伪标签可以根据数据的内在分布指导学习。通常情况下，来自同一类的图像应该更靠近伪标签空间。在本文中，计算特征向量距离并构造相似矩阵来指导模型学习。

本文中的无监督语义学习算法首先需要根据提取的深度特征计算每对数据点的相关度距离。相关度距离可表示为式（1），其中ρXY是相关系数，用来衡量随机变量X与Y相关程度，计算方法如式（2）所示。

ρXY取值范围是［-1，1］，当ρXY=0 时，说明变量和相互独立，ρXY的绝对值越大，则表明X与Y相关度越高。

在获得数据点之间的相关度距离之后，本文通过设置距离阈值ds=(ml-ασl)，dd=(mr-βσr)，将距离小于ds的数据点视为语义相似的数据对，距离大于dd的点视为语义不相似的数据对。其中α和β分别是控制距离阈值ds和dd的超参数，ml、mr是相似度距离直方图的左半部分和右半部分的平均值，σl、σr是相似度距离直方图的左半部分和右半部分的标准偏差。基于距离阈值继而构造相似矩阵S：

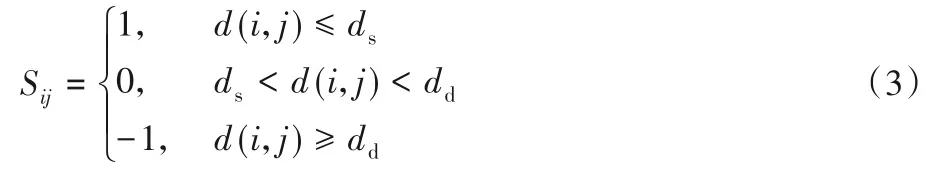
其中：d(i，j)表示数据点xi和xj的深度特征的相关度距离。如果xi和xj在语义上相似，则Sij被设为1；如果它们在语义上不相似，则为-1；当Sij设置为0时表示不确定是否相似。

2.2.2 哈希学习

学习得到相似度矩阵之后，VGG16 网络中第FC7 层连续特征变量Z需要分别经过4 个哈希层的联合学习获得不同哈希码。对于训练样本为g的数据，用相似度矩阵S作为图像之间相似度关系的参考。为了获得单层长度为K的二进制代码，本文定义单层哈希损失如式（4）：

其中：bi是数据点xi的哈希码；Hij是数据点xi和xj得到的哈希码的内积。从连续变量Z到二进制代码变量B的转换是有损信道，而且不同哈希码长度之间的信息量有交融与重叠，因此本文将特征向量Z分别通过L个哈希层（本文L设为4），每个哈希层输出不同位哈希码bl，通过多层哈希结构的损失函数即式（5）进行联合学习。

为了获得bi需要通过二值化处理，一般将符号函数b=sgn(z)作为哈希层顶部的激活函数来执行，即式（6）。

但是符号函数是非光滑和非凸的，它的梯度对于所有非零输入都是零，且在零处定义为错误。这使得标准的反向传播对于训练深网络是不可行的，即梯度消失问题［22］。针对梯度消失问题，本文将使用tanh()来近似代替符号函数，因此，目标函数可以转化为式（7）：

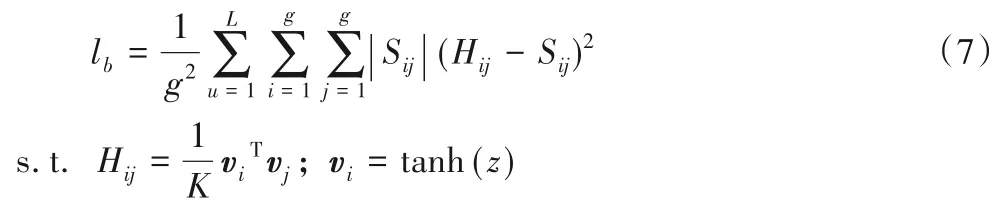
通过此损失函数约束模型最小化离散的汉明空间与连续空间的差别，最终可以获得较高精确度的不同位数哈希码。根据以上分析，本文模型将分为训练阶段和测试阶段两个部分，分别如算法1和算法2所示。

算法1 模型训练阶段。

输入 训练图像集X=，参数α和β，batchsize大小24；

输出 神经网络的参数θ、W和训练图像的哈希码B。

步骤1 初始化VGG16 网络的参数，使用神经网络前馈算法在VGG16 模型上提取数据的FC7 层输出，得到连续特征Z；

步骤2 根据式（1）和Z计算两两数据点的相关度距离；

步骤3 根据式（3）得到所有的伪相似矩阵S；

步骤4 从训练集中随机选取一个小批次（mini-batch）的训练数据；

步骤5 将小批次的训练数据通过网络得到初始的不同哈希码；

步骤6 根据式（7）并使用反向传播算法更新参数；

步骤7 重复步骤4～6，直至迭代次数完成。

算法2 模型测试阶段。

输入 查询图像q；

输出 查询图像q的不同哈希码。

步骤1 通过对输入图像的直接前向传播计算神经网络的输出。

步骤2 利用式（6）直接计算哈希码。

3 实验结果与分析

3.1 数据集

本文在FLICKR25K 和NUSWIDE 两个公共基准数据集上进行实验分析，数据集的说明如下：1）FLICKR25K 数据集包含从Flickr网站收集的25 000张图像，每个图像都是手动标注的，且至少是24 个标签中的一类。本文随机选择2 000 幅图像作为测试集，并使用剩余的图像作为数据库，从中随机选取10 000 幅图像作为训练集。2）NUSWIDE 数据集是大规模数据集，包含81 种图像类别，每个图像都用一个或多个类别进行注释。本文使用21个最常见类别（195 834张图像）的子集，从中随机选择5 000张图像作为查询集，并从剩余图像中随机选取10 000幅图像作为训练集。

3.2 实验环境与参数

本文所有的实验均在Ubuntu Server 18.04 操作系统，显卡为TITAN-XP 12 GB*6，内存为32 GB*4的计算机上进行，使用TensorFlow1.8.0 实现所提出模型，学习率设置为0.001，batchsize设置为24，使用动量优化法优化模型。

3.3 结果分析比较

为了检验本文模型效果，与ITQ（ITerative Quantization）［26］、SH（Spectral Hashing）［27］、DSH（Density Sensitive Hashing）［28］、SpH［9］、SGH（Stochastic Generative Hashing）［29］、DeepBit（Learning Compact Binary Descriptor）［30］、SSDH（Semantic Structure-based unsupervised Deep Hashing）［31］模型比较，使用平均精度均值（mean Average Precision，mAP）和查准率-召回率曲线（Precision-Recall Curve，PRC）来评估在两个数据集上的检索效果。

mAP 是指所有类别平均精度（Average Precision，AP）的平均值，AP 是每个类别图像的平均精度。假设系统返回t张检索到的图像，分别是x1，x2，…，xt；设有M类，则每个查询数据i的AP计算方法见式（8），mAP计算方法见式（9）。

在FLICKR25K 上和NUSWIDE 数据集上的mAP 比较结果如表1 所示。从表1 可以看出，本文模型在FLICKR25K 数据集上的16 bit、32 bit、48 bit 和64 bit 哈希码的性能分别比最好的浅层模型SGH 的mAP 值要高9.0、10.8、11.3 和11.3 个百分点，比无监督深度学习模型DeepBit 要高13.3、14.3、12.9和11.9个百分点，比SSDH要高9.4、8.2、6.2和7.3个百分点。在NUSWIDE 数据集上16 bit、32 bit、48 bit 和64 bit 哈希码的性能分别比最好的浅层模型SGH的mAP值要高17.1、20.2、21.9 和21.6 个百分点，比无监督深度学习模型DeepBit要高28.6、25.5、21.4 和20.9 个百分点，比SSDH 要高5、5.2、6.4、5.9 个百分点。从上述结果分析可知，本文模型在捕捉图像视觉语义方面表现出色，原因是不同哈希码之间互相限制，互相学习。本文模型在使用长度为16 bit 哈希码的mAP值要略小于其他长度，可能是16 bit的哈希码未能完全覆盖图像语义，但是在48 bit 之后mAP 值就稳定下来。需要注意的是，NUSWIDE 上的结果略小于FLICKR25K，可能是由于NUSWIDE 的图像类内和类间距离没有完全划分准确。但是，在达到相同检索准确率的要求下，本文模型可以用长度更短的哈希码来实现。

表1 两个数据集上不同模型的mAP对比Tab.1 Comparison of mAP of different models on two datasets

32 bit哈希码在FLICKR25K数据集上的PCR如图2所示，在NUSWIDE 数据集上如图3 所示。图中查准率是检索到的该类图像与检索到的所有图像之比，召回率是检索到的该类图像与数据库中所有的该类图像数之比。从图2 和图3 中可以看出，随着召回率的增加，所有模型的查准率均会减少。然而，相同召回率下本文模型的查准率仍高于其他模型，相同精确率下本文模型的召回率也优于其他模型。例如，图2 中召回率为0.4 时，本文模型的查准率最高，为0.77 左右；当准确率值为0.7时，本文模型的召回率最高，为0.59左右。

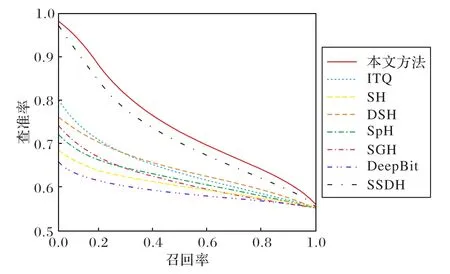
图2 FLICKR25K数据集上32 bit的PCRFig.2 32 bit PCR on FLICKR25K dataset

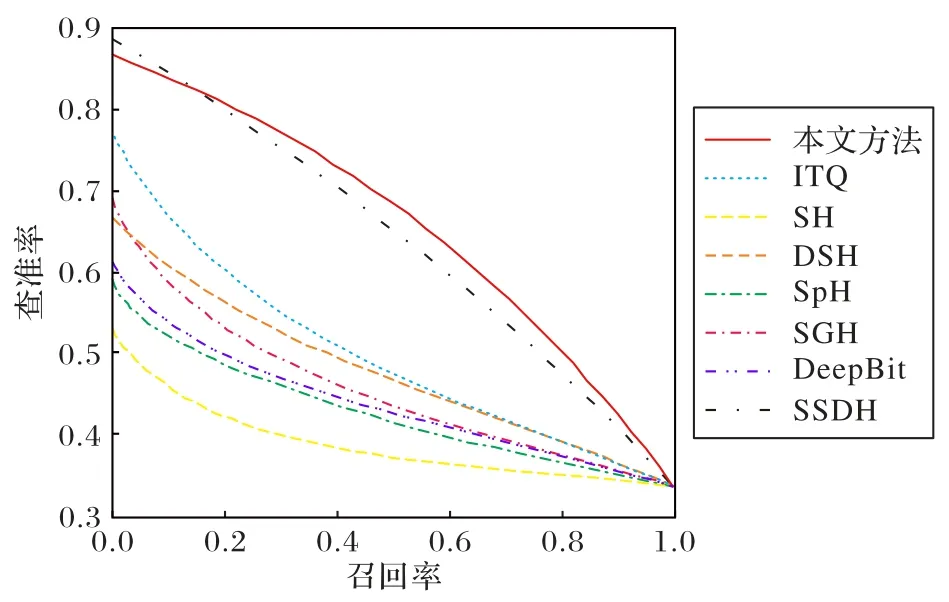
图3 NUSWIDE数据集上32 bit的PCRFig.3 32 bit PCR on FLICKR25K dataset

为了体现本文模型的效率优势，将本文模型的时间开销与SSDH进行比较，结果如图4所示，其中SSDH后的数字表示哈希码的长度。如图4（a）所示，在FLICKR25K 数据集上，SSDH 得到4 种哈希码分别需花费8 820 s、8 778 s、8 625 s 和8 740 s，SSDH 累积训练4 种不同长度哈希码共需要34 963 s，而本文模型训练时间为11 177 s，只占SSDH 训练时间的32%左右。如图4（b）所示，在大规模数据集NUSWIDE 数据集上，SSDH 分别需花费21 600 s、21 654 s、21 677s 和21 684 s，SSDH累计训练4 种不同长度哈希码共需要86 615 s，本文模型只需要79 860 s，与SSDH 相比减少了6 755 s。从上述结果比较分析中可以看出，本文模型由于集成了4 个不同哈希层，可大大节约训练时间，尤其针对于较大规模数据集的图像检索具有更为显著的优势。

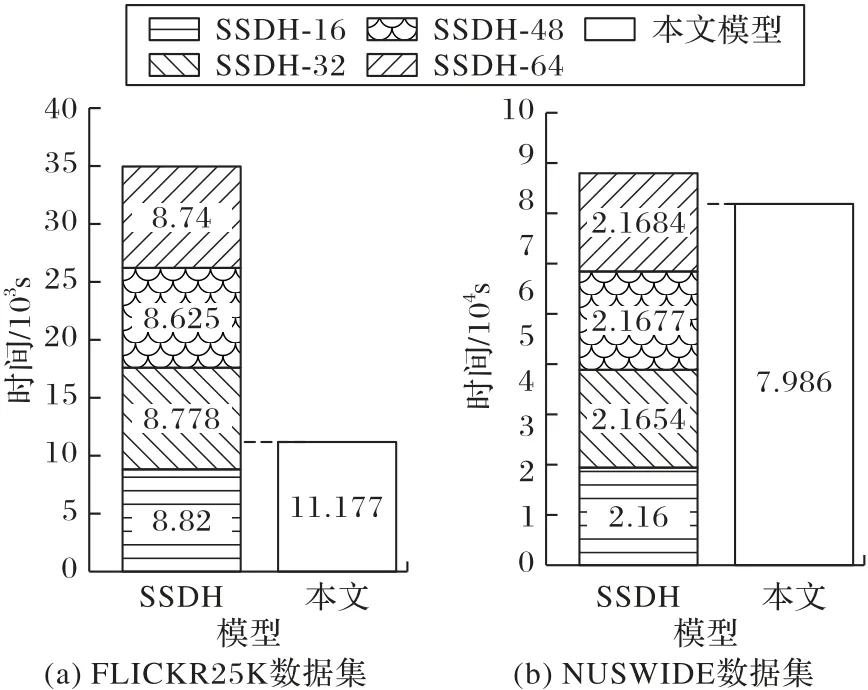
图4 本文模型与SSDH模型的时间开销对比Fig.4 Comparison of time cost between the model in this paper with SSDH model

3.4 消融实验

为了检验提出模块对所取得结果的贡献，本文进行了一项消融研究，结果如表2所示，其中：De表示使用欧氏距离，Dc表示使用余弦距离，Dr表示使用相关度距离，lb表示使用并行多层损失函数。通过表2 数据可以看出，使用欧氏距离或余弦距离的模型由于自身计算方法限制，都不能达到使用相关度距离的精度，例如FLICKR25K 数据集上使用相关度距离的16 bit 结果0.683 比使用其他距离的模型分别高7.4 和5.1 个百分点。另外，使用并行多层损失函数的模型都比原来使用单层损失函数的模型精度要高，例如大规模数据集NUSWIDE上同样使用相关度距离时，加上并行多层损失函数的模型使得精度分别提高7.4、8.7、9.7和9.7个百分点。因此，通过上述结果分析表明，本文模型能够更好地捕捉图像间细微的语义区分，缓解哈希码的信息冗余程度，从而提高生成哈希码的质量及图像检索的性能，特别是对于大规模数据集在检索精度和时间方面都得到更多的提升。

表2 消融研究对比Tab.2 Comparison of ablation studies

4 结语

针对无监督哈希学习中语义信息学习不充分、哈希码长度更改一次就必须重新训练且没有考虑不同哈希码之间联系等问题，本文提出了基于相关度距离的无监督深度并行哈希检索模型。该模型使用卷积神经网络学习图像特征，利用相关度距离计算特征语义相关性从而构建伪标签矩阵指导哈希函数学习，将不同bit 哈希层联合学习得到最合适的哈希码。在FLICKR25K 数据集以及更大规模的NUSWIDE 数据集上，通过与其他模型的实验结果比较分析，表明本文模型的检索效果得到提升，并且模型训练时间明显降低。本文模型无需额外提供监督信息，可以同时学习不同长度的哈希码，并且不同长度哈希码之间也可以互相学习，从而逐步接近原始特征空间，因此，本文模型适用于标签信息获取代价高昂的大数据时代，对于大规模图像检索具有一定实际应用意义。