居民公交出行链重复性量化分析及其出行规律研究*

崔洪军 孙婉茹 赵 锐 朱敏清 李 霞

（1.河北工业大学土木与交通学院 天津300401；2.河北工业大学建筑与艺术设计学院 天津300401）

0 引 言

绿色出行理念被广泛接受，公共交通以其大运量、高准点率、低碳环保等特点被出行者广泛采用，因而，产生了大量的公共交通出行数据。通过海量的出行数据可分析出乘客的出行规律，而这些规律性信息对于交通规划与管理工作有着重要的参照性意义。

呙娟[1]基于出行个体，结合出行强度、出行行为鲁棒性、时空关联谱等对个体的出行特征进行了详细研究，得出了所研究个体的相关出行特征；何兆成等[2]针对居民历史出行，利用DBSCAN聚类算法对其进行分析，并提出了基于不同出行模式的出行特征周期性分类方法，并结合k-means++算法对居民出行的规律性进行了评价；王俊兵[3]利用融合后的公交IC卡数据、公交基础运营数据基于时空判别算法对乘客的公交出行链进行了提取，继而分析了公交乘客的出行特征；朱亚迪等[4]通过隐马尔可夫模型对乘客多日的出行链进行了提取，并结合用地性质、识别了乘客的出行目的；T.Kusakabe等[5]将出行调查数据与IC卡数据相融合，基于朴素贝叶斯分类器法提取了IC卡数据集中缺失的出行属性信息；Ma等[6]基于公交IC卡数据独有的时空特性，对乘客的出行行为模式采用空间聚类的方法进行识别，并分析了乘客的出行行为规律；张晚笛等[7]基于多时间粒度对乘客的地铁出行规律进行了研究。杨光[8]对快速公交乘客的出行的时空规律特征进行了研究。Chu等[9]利用时空关联理论分别分析了智能卡乘客在指定车站的乘降数量及关联行程。Medina等[10]对出行活动进行聚类，并利用分层选择模型对为期7 d的连续出行活动进行了分析。

由现有文献可知，学者多侧重于对乘客出行时空规律的分析，而对乘客出行规律自身的排列顺序鲜有研究。笔者以关键特征事件发生顺序作为出行重复性的度量指标，通过度量不同的事件发生顺序可对出行规律性进行刻画，以揭示不同时空刻度下的出行时空变化规律。

1 居民公交出行链

出行链（trip chain）是指居民在1 d中一系列的实际出行活动依照发生时间的顺序首尾衔接而形成的出行轨迹。出行链可以呈现居民的出行方式、出行目的等，而研究出行链有助于分析乘客的出行变化规律。

在实际出行中，大部分居民为了提高效率会尽可能在1个出行链中将1 d的出行安排完成，因此，多数居民的出行规律是较为固定及简单的[11]。例如1名乘客在t B1时刻于B1站点上车，在t A1时刻于A1站点下车；完成一系列活动后在t B2时刻于B2站点上车，在t A2时刻于A2站点下车；又经过一系列的公交、非公交出行后，在t B n时刻于B n站点上车、在t A n时刻于A n站点下车，完成当天的最后1次公交出行；其时空关联特征见图1。

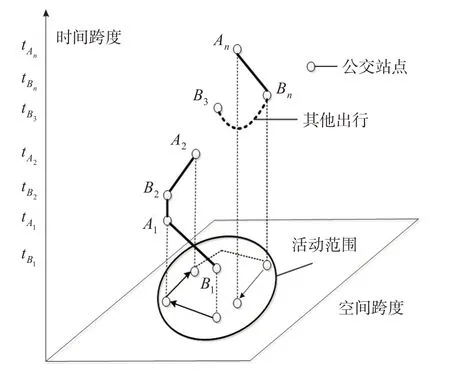
图1 公交出行链时空关联特征示意图Fig.1 Temporal-spatial correlation features of the bus-trip chain

公交IC卡刷卡乘车作为乘客乘车的主要付费方式，包含了大量的乘客出行信息，基于自动数据采集系统（automatic data collection system，ADCs）可得到海量的电子交易数据。利用ADCs进行上车站点识别[12-13]，基于推断乘客下车站点所用的经典假说[14]推断乘客的下车站点。经过上下车站点匹配，可得到完整的乘客出行链；基于此，可对公交出行规律进行分析研究。

2 公交乘客出行链的量化处理

每条出行链均包含了大量的出行信息，如出行时间、出行起点、出行目的地、逗留时间等。由于每位出行者的通勤方式、出行习惯等的不同，通常难以对多人多时的海量出行链数据进行量化分析。为了便于查找居民公交出行的规律，笔者按照出行地点划分，将居民的出行链转化为离散的出行序列。

通过利用排列关键特征事件顺序来呈现出行序列，从而表示特征事件的发生频率及发生次序。利用数学方法对每名乘客在连续多日的出行作如下定义：设乘客个体u出行所对应的随机过程为X u，随机变量X u表示X u中产生的特征事件。为识别特征事件的唯一性，假设每个特征事件均为1个离散变量x，x∈Eu（Eu为个体u出行时产生的可能出行特征事件集），且X u满足离散概率分布p(x)=P{X u=x}。需要指出的是，特征事件的x值由事件属性的组合唯一确定。因研究对象均为单个出行个体，故在后文省略下标u以避免冗余表达。用随机过程X={…，X-1，X0，X1，X2，…}表示随机变量Xi的有序集合，那么特征事件i与j间有序集合的任意有限出行序列可用有序子集={Xi，Xi+1，…，X j-1，X j}表示；其中，-∞＜i≤j＜+∞，⊂X。为了一致性和计算方便，笔者假设所有事件属性均是离散的。

以地点状态对乘客出行链进行量化处理，其出行序列的生成流程如下。

步骤1。读取公交乘客的出行链记录，并顺序读取出行者的时间、线路、站点等出行信息。

步骤2。按照研究时间段，构造完整的时间序列。

步骤3。对研究时间段内的出行信息作如下判断：若无行程记录，乘客出行地点不能推断，则在该次出行状态填“-1”；若不能推断乘客起讫点，出行地点无法推断，则在该次出行状态填“0”；若判断为乘客所在的第1个且滞留时间最长的地点，则在该次出行状态填“1”；若判断为乘客所在的第2个且滞留时间次长的地点，则在该次出行状态填“2”。

步骤4。以此类推，以-1，0，1，2，…补全所有出行状态，形成的序列即为基于出行地点状态划分的个体出行序列。

3 出行链重复性量化分析

由于乘客出行具有时空反复性，其常规出行多以居住地为中心，反复访问某些固定地点并逗留近似时长[15]。而采用公交出行的乘客，该规律更为明显。由此引出出行重复性的定义：一定时间跨度内，出行者访问某一地点并逗留相近时长的反复程度称为出行重复性。出行重复性可对乘客的出行偏好进行定性描述，而对出行规律的定量分析则需从数学角度对重复性进行量化处理。

3.1 出行序列的信息熵

为了量化出行序列的重复程度，引入信息熵对出行重复性进行定量描述。在信息论中，1个过程的随机性或不可预测性可以用信息熵来衡量，即信息熵可度量对每个随机变量预测时所需的平均信息，故在此将描述出行重复性的信息熵定义为：根据现有信息推断乘客未来可能出行的地点所需的信息值，单位为比特（bits）。

基于前文对出行序列的量化过程可知，概率分布p(x)决定了随机过程X u（即出行特征序列）的规律性。无论出行特征属性的顺序如何，满足概率分布p(x)=P{Xu=x}的随机过程X u的信息熵H(Xu)见式（1）。

式中：X u为出行序列中被看做随机变量的乘客访问地点状态。总的来说，信息熵为研究时段内出行地点被乘客访问概率的方差。假设乘客只有唯一备选访问地点，其出行序列信息熵值为0；随着乘客出行地点在研究时段中分布越均匀，其信息熵值就越大。

3.2 出行序列熵率

信息熵从乘客访问地点重复性角度进行考量，但未考虑到时间变化对其的影响。与此同时，随机变量Xi的条件概率分布也取决于事件Xi-1，Xi-2的分布结果（p(Xi|Xi-1，Xi-2，…)≠p(Xi)），即出行地点排列的先后顺序。因此，本文引入熵率与信息熵形成综合量化出行重复性的指标。

熵率H'(X)考虑了乘客访问地点排列顺序对出行重复性的影响，将其定义为子序列随n逐渐增大时其信息熵H(X)的收敛速率，见式（2）。

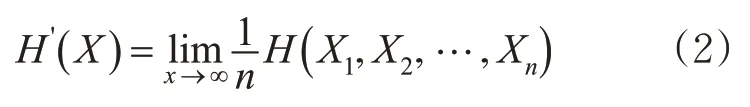
式中：H(X1，X2，…，Xn)为由子序列X1，X2，…，X n定义的联合变量序列的熵率。

在所有平稳随机过程中式（2）极限必存在[16-17]，见式（3）。

式中：p n为长度为n的子地点状态序列的联合分布概率。

由式（2）～（3）可知：熵率为随机过程X中每个新生成的特征事件在已有特征事件中的平均信息熵。也就是说，它反映了每个新访问地点对乘客整体出行地点序列信息熵的影响变化情况。出行序列熵率的上限为出行序列信息熵的值；当出行地点状态序列中乘客访问的新地点可由之前的地点状态唯一确定时，其熵率为0。

本文基于Burrows-Wheeler转换（BWT）[16]计算熵率，其具体计算过程参阅文献[18]。在任意平稳随机过程X中，通过BWT转换将有限记忆序列转换为分段无记忆序列，通过该过程可以计算出原始序列过程的熵率[19]。将转化后的序列划分为等长的s段，根据式（4）估计每段的结果分布。其中，N s(x)表示字符x在段落s中出现的次数，任意段落s获得的信息熵可由式（5）得到。最后，随机过程X即乘客出行序列的熵率可通过每一段信息熵的均值得到，见式（6）。

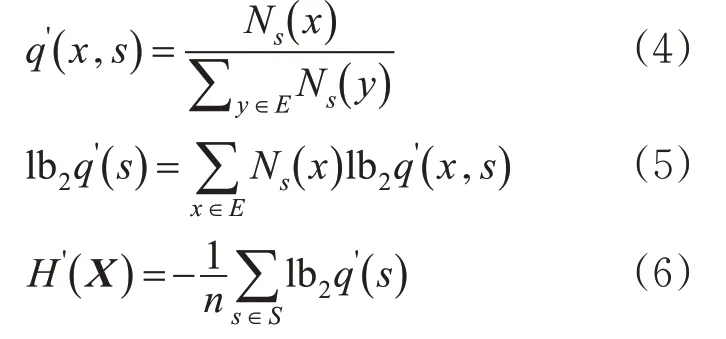
总的来说，熵率是对一系列事件中产生新信息多少的度量。之前的数据中包含的信息越多，可以为后续数据分析提供的信息就越多，可以挖掘的新信息就越少，即熵率值就越小。因此，熵值率可以用来量化乘客出行重复性。出行序列熵率越小，乘客的出行重复性越高，出行规律性越强。

4 居民公交出行规律

4.1 基于量化指标的出行规律

以石家庄公交智能卡乘客2018年1月1日—31日的IC卡出行数据为例，经上下车站点识别匹配，共得到46 923条完整的乘客出行链。对复杂的出行链按照出行地点的状态进行量化，以1名持卡人出行记录为例；其2018年1月1日—31日的部分出行记录见表1。

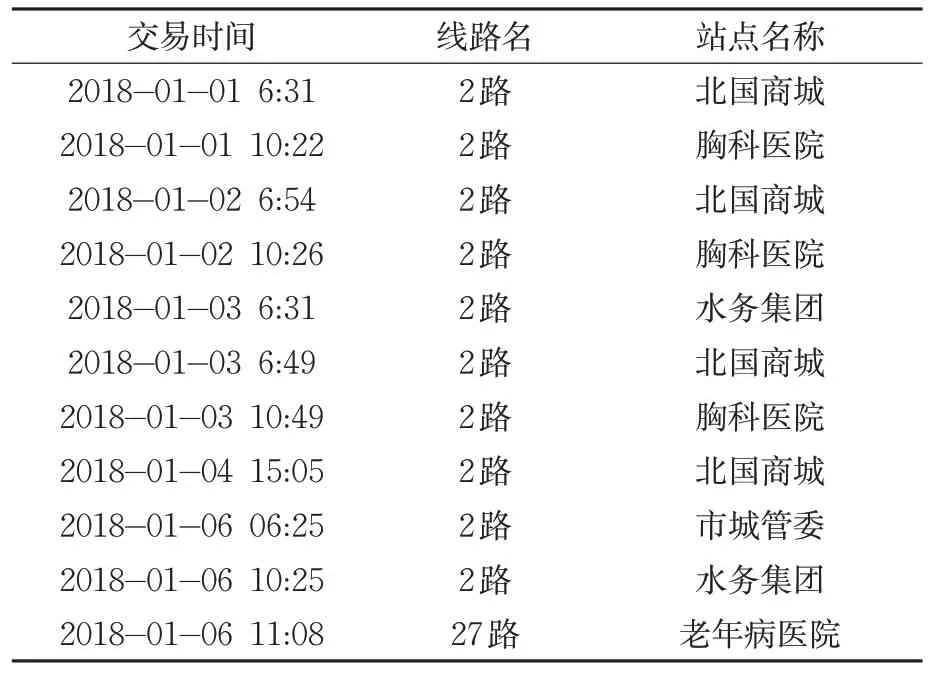
表1 持卡人出行记录Tab.1 Cardholder's travel records

以出行地点状态为依据将其出行特征序列进行排序，故可将此持卡人在2018年1月1日—31日期间的出行序列简化为（1,2,1,2,3,1,2,1,4,3,5）。基于上述方法将石家庄乘客出行数据中匹配成功的46 923条出行链进行量化处理，将其离散为简化的出行序列，后文将基于此进行出行规律的量化分析。

将乘客46 923条出行特征序列依照3.1和3.2所述方法，计算乘客出行序列的信息熵值及出行特征序列的熵率，其分布情况见图2～3。其中，信息熵分布的均值为2.53 bits，熵率分布的均值为1.13 bits/事件。

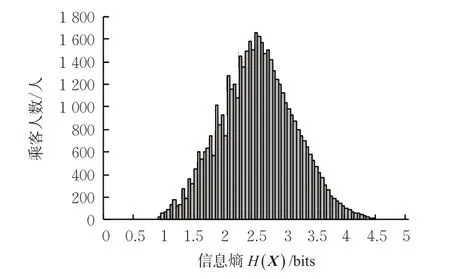
图2 智能卡乘客出行序列的信息熵分布Fig.2 Distribution of entropy across passengers using smart cards

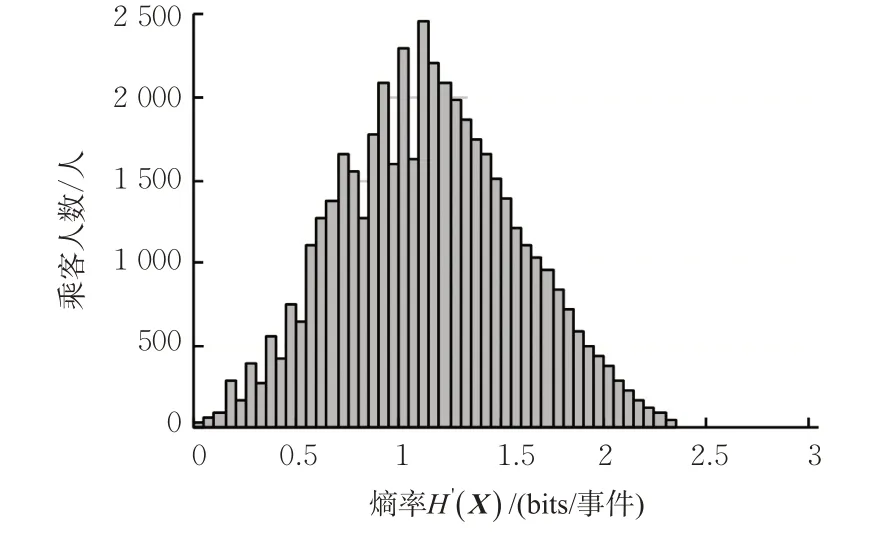
图3 智能卡乘客出行序列熵率分布Fig.3 Distribution of the entropy rates across smart card passengers

结合图2～3可以观察到：出行序列的信息熵与熵率二者均值之差为1.4 bits，这意味着考虑乘客出行事件的发生顺序可使乘客出行重复性量化时的不确定性显著降低。由出行序列信息熵及熵率的性质可知，乘客的出行序列信息熵越大、熵率越小其出行链的重复性越高，出行者的出行规律性越强。若1个人只在家庭和工作地(p(home)=p(work)=0.5)之间出行，则其熵为1 bits，等同于抛硬币所产生结果的信息熵（信息熵为1 bits）。而熵率是考虑了事件发生顺序时信息熵的值，结合出行链的特征，文中考虑了乘客的出行地点序列及目的地逗留持续时间，有助于出行规律性分析。

4.2 以持卡类型区分的群体出行规律

分别选取成人卡、老年卡、学生卡3类持卡乘客各200名，计算其出行序列的信息熵及熵率。为直观获取公交乘客出行规律，将上述600名乘客出行序列的信息熵及熵率计算值绘制见图4，并计算不同持卡类别群体的信息熵和熵率均值见表2，以此分析其出行重复性及出行规律。

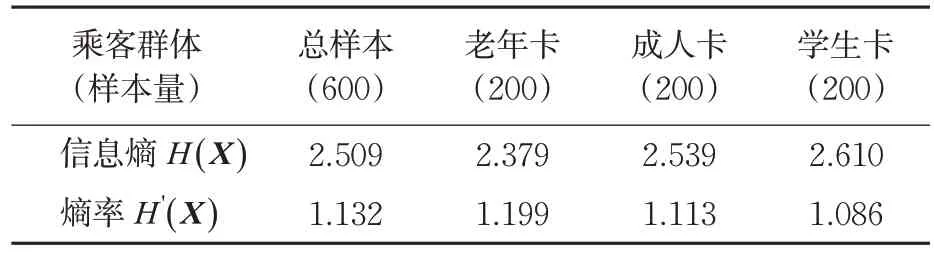
表2 所选乘客出行重复性量化指标统计Tab.2 Quantitative indicators of the repeatability of selected passengers'travel

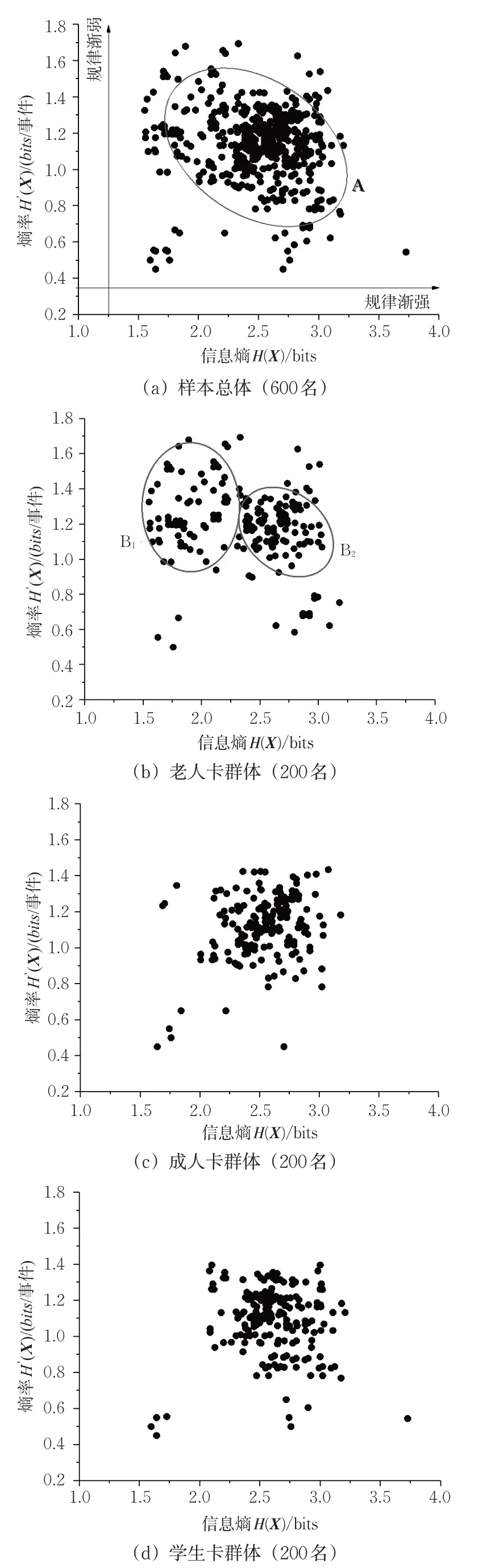
图4 所选乘客出行重复性量化指标散点图Fig.4 Scatter of the quantitative indicators of the repeatability of the selected passengers

图4（a）中数据点虽较为散乱，但总体出现规律性。借助图形A将多数样本点圈出，圈中样本点为总量的90.83%，说明样本总体聚集程度较高，进行群体出行规律分析存在一定意义。由表2可知，总体样本量信息熵与熵率的均值与理论计算值较为接近，说明该样本量具有一定的代表性，符合统计学分析的原则。

通过对比各不同类型乘客出行序列的信息熵及熵率，可以了解不同类型乘客出行的日常规律。图4（b）～（d）为各类型乘客出行重复性的量化散点图，结合表2中数据可以发现以下规律。

1）老年人、成年人、学生群体出行规律呈递增趋势，在散点图聚集程度、信息熵和熵率数值均有体现。老年人群体出行安排相对自由，而成人群体和学生群体则被通勤时间限制，具有较明显的出行规律。

2）成人卡与学生卡持卡乘客的信息熵和熵率数据点均比较集中，即上述2个群体中多数人出行重复性一致，出行规律趋同。通过对比表2中的数据得出，持学生卡群体出行重复性更高、规律性更强（熵值较大，熵率值较小）。分析其原因为学生群体主要通过公交进行上下学出行，时间比通过公交通勤的成年人更为固定和规律，且成年人出行时间、出行目的、逗留时长比学生更多样，故学生群体出行规律相对较强。

3）在图4（b）中，持老年卡乘客的信息熵和熵率计算值相对分散，即该群体中，出行重复性难以统一描述，很难直接捕捉到老年人群体的出行规律，因此辅以图形B1和B2进行分析。根据前文总结的规律，B1群体熵值较低、熵率值较高，则其出行无明显重复性，以休闲娱乐等弹性出行为主；B2群体与成年人、学生群体的熵值、熵率值较接近，出行重复性高，出行规律明显，结合目前城市生活现状，则可考虑为一部分老年人承担家庭中接送学童上下学的任务，与学生群体的通勤规律相似。

4.3 基于重复性量化的个体出行规律

结合前文分析，选取3种典型出行模式的乘客出行序列进行分析：时空常规出行（学生卡）、时空常规出行（成人卡）、时空非常规出行（老年卡）。为保证所选乘客对其所在群体具有代表性，选取图4中信息熵与熵率值数值与样本均值接近的3名乘客，见表3。

表3 所选乘客出行重复性度量指标统计Tab.3 Quantitative indicators of the repeatability of selected passengers'travel

根据不同地点的出行序列分布情况，结合乘客活动的持续时间，可得到其出行序列分布情况分别见图5～7。图中不同图样为该乘客的不同出行地点，而黑色代表无法推断的出行所处位置。

如图5所示，将该持卡乘客的出行规律分为2个阶段。1月1日—18日，其工作日时段固定访问3个出行地点，且出行时间、逗留时长均保持稳定，单日出行即显示出明显规律；1月18日—31日，其单日出行规律亦较明显。而其周末2 d在固定时段按照一定次序访问3个地点，以双日出行呈现规律性。由ADCs数据可知，该持卡人所持卡种为学生卡，持卡人为学生，于1月19日进入寒假。根据上述信息可以推断出该乘客前一阶段为上、下学出行，而后一阶段可能为课外补习的出行，周末为娱乐或其他出行。总体来说，其出行重复性较强，出行规律明显，且结合图4（d）可知，该乘客具有群体代表性，对公交线路、时刻表规划的改进具有重要意义。

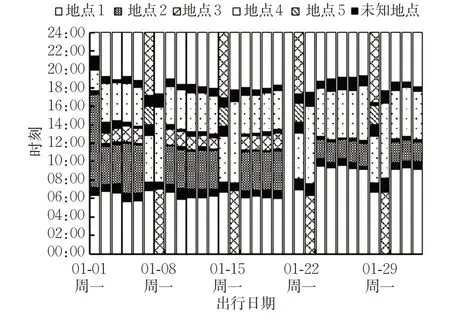
图5 所选卡号为A的乘客出行活动序列Fig.5 Activity sequence of Cardholder A

由图6可知，该持卡乘客1个月内出行规律较明显，每周以工作日和休息日2种出行模式交替出现，具有明显的通勤特征。有别于图5乘客的是，该乘客工作日出行地点更加多样性，可能由其工作性质决定，且该乘客在每周一13：00—15：00均会产生未知出行，考虑其采用了其他出行方式（如出租车）完成本次出行。虽然该乘客工作日出行模式并不完全一致，但总体呈现规律性，出行重复性较强，此结论亦可由表3信息熵与熵率的值判断得出。

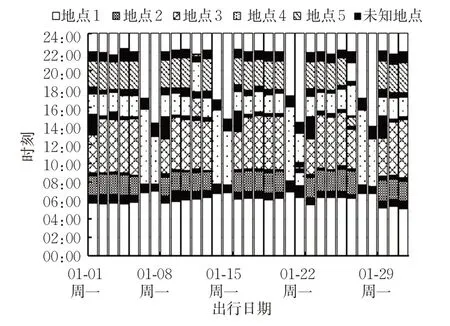
图6 所选卡号为B的乘客出行活动序列Fig.6 Activity sequence of Cardholder B

图7直观来看出行规律较模糊，出行重复性低，出行规律不明显，但其出行序列的信息熵要高于均值，可以推测出该持卡用户的出行应较为规律。分析图像可以发现，该持卡乘客的出行序列间隔2周显示出重复性，即第4周、第5周与第1周、第2周出行序列重复性。结合表1，可作出如下推断：该用户在接下来的日历周期中有较大的可能会重复第3周的出行规律。

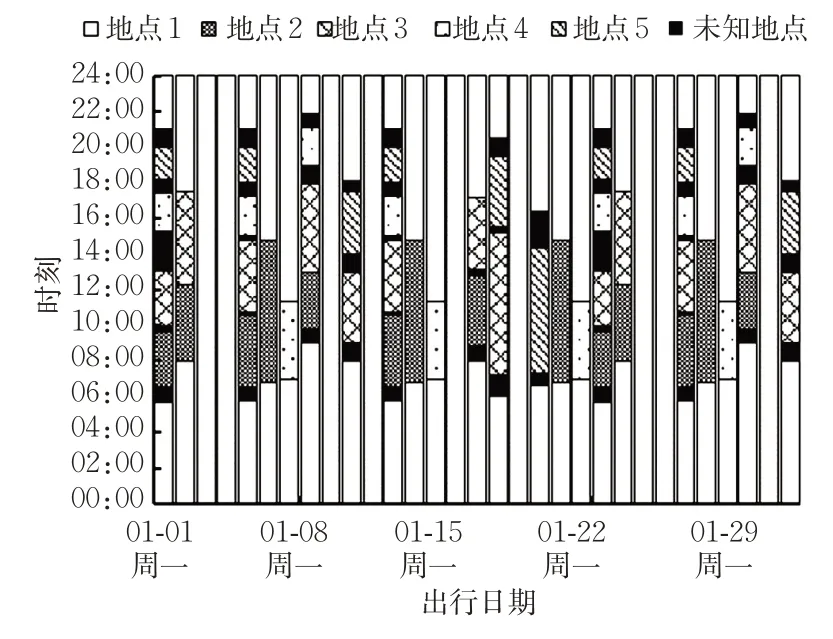
图7 所选卡号为C的乘客出行活动序列Fig.7 Activity sequence of Cardholder C

4.4 与其他出行规律分析的区别和联系

以往的出行规律研究（仅针对公交）大多通过获得某地区的出行数据，从中得到出行时间、出行地点、出行目的、逗留时长等信息，通过概率统计的方法对该地区的出行偏好进行“解读”，大多在数据获取、数据处理以及规律分析结果应用等方面进行创新及改进。以图7中卡号为C的乘客为例，可以分析其出行时间在06：00—08：00的概率最高，为48.39%；除居家外，该月在地点2逗留时间最长，时长69 h。从这个角度来看，该乘客出行规律并不明显。

本文引入信息熵和熵率将出行链重复性进行量化，在此基础上对出行数据的分析更多的是1种“辨识”：利用量化指标判断群体或个人出行规律的强弱性。本文研究可根据信息熵和熵率的聚集程度（见图4）判断群体出行是否有相似规律，从宏观掌握居民公交出行的群体特征；也可根据信息熵和熵率数值大小判断个人出行是否有规律，从微观层面分析乘客个人出行规律。同样以图7中卡号为C的乘客为例，根据信息熵高于样本均值2.53 bits、熵率低于样本均值1.13 bits/事件，分析其出行具有一定的规律性，通过分析发现该持卡乘客的出行序列间隔2周显示出重复性。

虽然2种分析方法的角度不同，但对出行规律的分析是相互补充、相互完善的。通过综合考虑2种分析角度，进行出行规律强弱判断与出行规律挖掘，可有针对性地对不同群体制定更为精细化、人性化的运营服务对策，从而为提高公交服务水平、缓解城市拥堵压力提供新思路。

5 结束语

本文基于公交IC卡数据，利用自动数据采集系统中数据集确定乘客的上车时间，并基于出行链经典假设对乘客的公交出行链进行了提取。通过数学方法结合随机过程将出行者多日的出行链离散为出行序列。利用信息熵和熵率对乘客的出行重复性进行量化，并以石家庄公交智能卡乘客出行数据为例进行了实证分析。结果表明，乘客出行重复性可通过信息熵和熵率进行量化，信息熵越大、熵率越小，其出行重复性越高。

本文是以公交IC卡数据为基础的分析方法，多适用于以公共汽车为主的中小城市公交规律分析。考虑到大城市轨道交通、共享交通的发展，需要综合广义公交系统多源数据信息，从而进一步分析居民公交出行规律。