高速动车组接触器复合应力加速模型研究
2021-07-29周建升
周建升,唐 辉,刘 广
(1.中车青岛四方机车车辆股份有限公司,山东青岛 266000;2.中国铁路广州局集团有限公司广州动车段,广东广州 510000;3.西南交通大学机械工程学院,四川成都 610031)
0 引言
随着动车组运营规模的提高,列车运行安全性要求也越来越高。接触器作为完成电路切换、控制与保护功能的关键元器件[1],广泛应用于高速动车组的电气系统。一旦发生故障,将直接影响高速动车组正常运行。因此,对接触器进行可靠性分析具有重要意义。
研究接触器可靠性的方法需要基于产品的寿命数据[2-3]。而高速动车组为了保持安全运行,接触器等元件在失效之前就必须进行更换,避免事故的发生。因此为了得到足够的寿命数据,需要对接触器进行大量的寿命试验。随着生产技术的不断发展,接触器寿命不断提高,按照动车组上接触器的实际使用频率,寿命试验可能长达数年,而通过加速实验可以大量缩短试验时间[4]。
加速寿命试验的统一定义最早于1967 年由美罗姆航展中心提出[5]。该试验在进行了合理的工程及统计假设后,通过超出正常水平的应力对试验进行加速,利用统计模型将加速环境下的可靠性信息与物理失效规律下的信息进行转换,从而复现出在正常应力水平下的可靠性特征的数值估计[6]。即在不改变试验样品的失效机理的条件下,通过增大试验应力缩短试验周期,提高试验效率。
加速寿命试验属于统计试验范畴,试验中对产品所加的应力可以是温度、电流、电流、功率、湿度、机械应力等[7]。目前加速模型多为单应力模型,未考虑应力交互项。针对以温度为加速应力的单应力加速试验,阿伦尼斯(Arrhenius)在1880 年提出了阿伦尼斯模型,该模型指出产品寿命随温度上升而呈指数下降[8-9]。针对电应力的加速试验,其加速模型被物理上的数据证实符合逆幂率模型。同济大学的康劲松等在分析驱动电机系统中直流母线电容单一加速模型及加速系数的基础上,推导出了直流母线电容在温度—电应力同时作用下的加速模型和加速系数,并通过仿真分析进行了验证[10]。查国清等通过对智能电表的失效机理分析,设计并实施了加速试验方案,通过对试验数据的退化轨迹进行建模以及多应力加速模型的研究,对智能电表可靠性和寿命水平进行了综合分析[11]。
本文所依据试验施加温度和电流这两种接触器上最常见的应力。在加速试验的基础上,计算出了一种复合应力加速模型,并通过实验数据验证复合应力加速模型的准确性。
1 单应力加速模型
1.1 阿伦尼斯模型
由于接触器开合过程中,触头间会产生电弧,并且设备运行过程中线圈会出现发热现象,二者都会引起接触器工作环境的温度发生变化。温度改变将导致材料的性能发生变化,加速产品失效。阿伦尼斯模型是阿伦尼斯基于温度为加速应力提出的模型。

其中,L 为产品的寿命特征,如中位寿命、平均寿命等;A 为大于0 的常数;E 为与材料有关的激活能,单位为eV;K为玻尔兹曼常数,8.617×10-5eV/K;T 为绝对温度,单位为K(开尔文)。E/K 又称激活温度,单位为K。
激活能是一种反映温度对产品寿命影响的指标,在低于500 K 的情况下,对确定的反应,其激活能为常数[10]。这确保了加速寿命试验的可行性,而对于一般电子产品来说,温度应力一般不会超过500 K。
阿伦尼斯模型表明:产品的寿命特征随温度上升呈指数下降。故对模型两边同时取对数可得:

其中,a1=lnA1,b1=E/K,a1和b1均为待定参数。从阿伦尼斯模型可知,寿命特征的对数与温度的倒数呈线性关系。
1.2 逆幂律模型
在加速寿命试验中,电应力作为一种常见应力也可普遍作为加速应力。在接触器实际使用过程中,增大接触器触头间的电流,会影响接触器触头间的电弧。由于每次接触器开断触头间均会产生电弧对触头造成侵蚀,因此将电应力作为加速应力进行试验。
在物理上很多试验数据证明,电应力作为加速应力时,产品的寿命特征复合逆幂率模型[10]:

其中,L 为产品的寿命特征(如中位寿命、平均寿命等),A2为大于0 的常数,m 为与材料激活能有关的正常数,I 为电应力。
逆幂率模型表示产品的某寿命特征是电应力I 的负次幂函数。将模型两边取对数可得:

其中,c1=lnF2,d1=-m,c1和d1均为待定常数;I 大于0。
2 复合应力加速模型
产品在使用过程通常受到复杂的环境应力,对接触器而言会受到温度、电应力、湿度的影响。这些应力的综合效果对接触器的使用寿命产生了影响。但同时考虑多种应力对接触器的寿命影响将使模型过于复杂且不利于实际应用。对于接触器而言,电应力和温度对接触器寿命影响最大,因此本文加速模型只考虑温度及电应力的影响。
2.1 无交互项的复合模型
由于接触器本身的结构及工作原理较为简单,因此在忽略掉温度和电应力之间的影响的情况下。直接将温度与电应力的影响相乘便可得到一种简单的加速试验模型[10]。
经分析可知,温度加速模型服从阿伦尼斯模型,电应力加速模型服从逆幂率模型,将两种模型相乘可得:

对该模型两边同时取对数可得:

其中,a3=lnA3,b1=E/K,d1=-m,a3、b1和c1均为待定常数。
2.2 考虑交互项的复合模型
Eyring 等针对温度及电压作为加速应力的情况,于1941 年提出了广义艾林模型[7]。广义艾林模型为:

其中,A′、B′、C′和D′均为待定常数,K 是玻尔兹曼常数。若令L′=LT,再对上式两端同时取对数,可得:
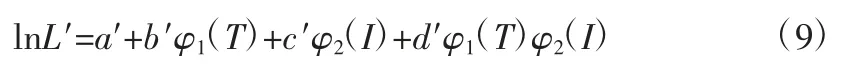
其中,a′=lnA′,b′=B′/K,c′=C′,d′=D′/K,φ1(T)=1/T,φ2(I)=I。上式中的第四项为温度应力与电应力的交互项,为简化模型实际使用中常忽视掉该项,但为了提高模型精度,需要对其交互项进行研究。
3 加速试验及模型参数计算
由于高速列车所用接触器额定电气寿命高达50 万次,且接触器所处工况常优于额定工况,故而接触器实际使用寿命次数将高于50 万次。常规寿命试验将耗费大量时间来对接触器进行寿命测试,为缩短试验周期且保证测试准确性,本文设计接触器在温度和电应力条件下的复合应力加速试验。
3.1 试验方法
根据阿伦尼斯模型,当单独取温度作为加速应力时,T0,T1,T2,T3,T4应按照温度梯度的倒数呈等间隔的原则进行温度选取,选取规则如式(10)所示:

其中,k=0,1,2,3;T0为常温条件,25 ℃;T4为极限工作最高温度,80 ℃。
根据逆幂率模型,在单独取电流作为加速应力时,应按照电应力参数的对数呈等间隔的原则进行选取:

其中,k=0,1,2,3。I0=35 A,为实际使用电流,I4=100 A,为额定负载电流值。根据式(8)计算出I1、I2、I3,将对应的Tk和Ik组合形成4 个梯度的复合应力加速条件。接触器额定参数见表1,加速实验条件见表2。

表1 接触器额定参数

表2 加速实验条件
3.2 特征寿命计算
根据接触器样本数据,进行接触器的威布尔分布计算和特征寿命计算。随着应力增大,接触器寿命逐渐缩短,需要针对不同测试应力调整测试间隔。因此条件1~条件3 测试间隔为接触器开断每1000 次,条件4 测试间隔为接触器开断每500 次,条件5 测试间隔为接触器开断每100 次。
以样品1 为例进行计算,实验共用5 个样品,即测试总量n=5,试验采用定数截尾法,在总样本数量的60%失效时停止试验,即3 个样品失效时。试验结束时不同条件下接触器开断次数情况如表3 所示。
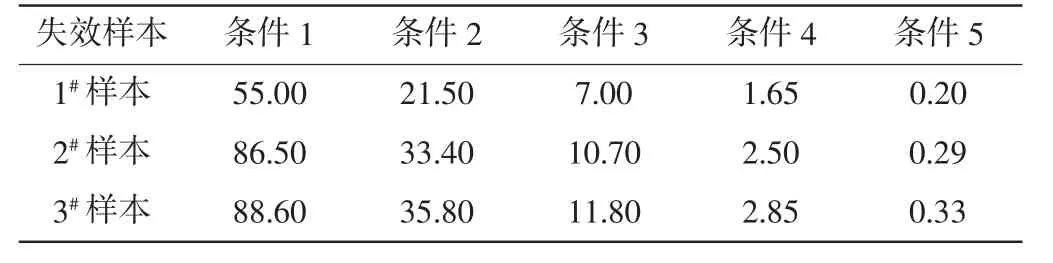
表3 接触器失效次数 万次
根据威布尔分布的定义,其累积分布函数为:

其中,c 为部件工作次数,β 为威布尔分布形状参数,η 为威布尔分布尺度参数。
对式(12)进行变换可得:
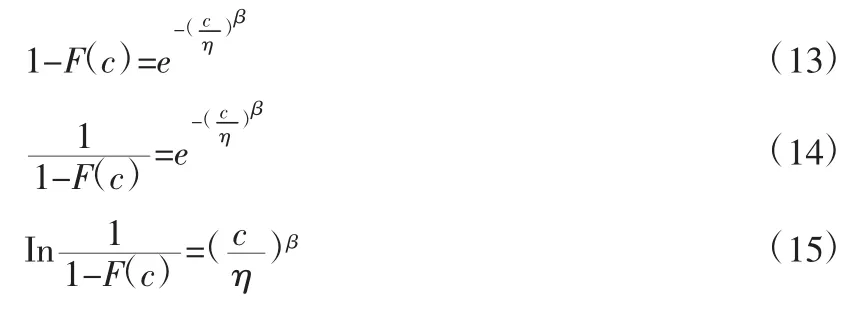
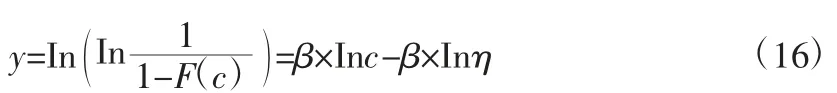
将Inc 看作自变量,y 看作因变量,β 即为拟合直线的斜率,直线与纵轴截距q=-β×Inη,则。由失效数据的中位秩确定。

其中,i 为累积失效数量,n 为测试总数量。
将样品1 失效数据带入上式后得到F(c),将测试数据进行变换以后,按照x=Inc 为横坐标,y 为纵坐标,在威布尔坐标图中进行描点(表4)。
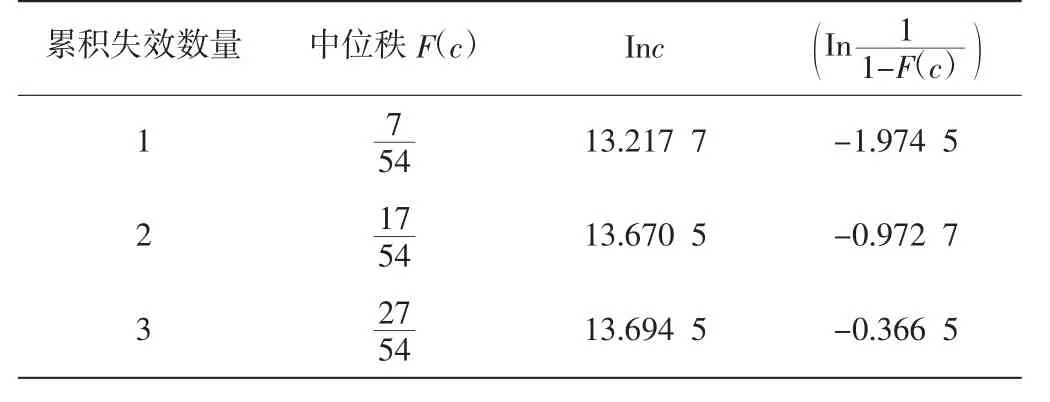
表4 威布尔分布待拟合数据
表4 中数据通过最小二乘法拟合拟合后图像如图1 所示。
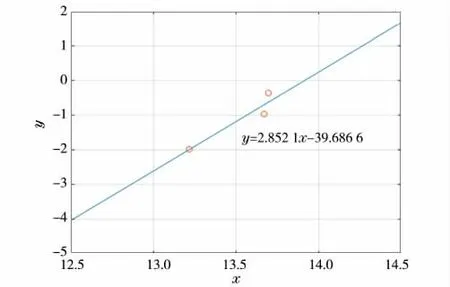
图1 威布尔坐标图
根据坐标中数据的拟合结果,得出形状参数和尺寸参数。
由图1 可知,拟合后直线为y=2.852 1x-39.686 6,拟合直线斜率β=2.852 1,直线与纵坐标轴截距q=-39.686 6,则尺度参数为η=1.104 4×106。由此得到第一个接触器样品的威布尔形状参数β 和尺度参数η。
同理得到其余4 组接触器样品的威布尔形状参数β 和尺度参数η(表5)。

表5 接触器威布尔分布特征参数
3.3 复合模型参数计算
按照忽略应力之间的相互影响,直接相乘的模型进行拟合。
式(7)中,由b1=E/K,激活能E 选取为0.534 eV,计算可得b1=6197.05 K。将加速实验所得特征寿命数据带入式(7),可解得不考虑温度与电应力之间影响的模型为:
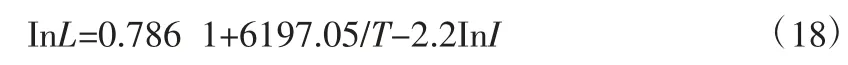
将式两边同时取自然常数为底数的指数运算得:

将加速实验特征寿命数据带入式(9)中解得参数为:

带入式(9)可得复合应力加速模型为:
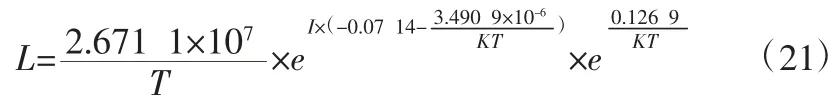
4 应力模型准确性对比分析
将常规实验的条件参数T=298.15 K、I=35 A 代入无交互项的加速应力模型即式(19)中,可得预测结果L1=936 108。
将常规实验的条件参数T=298.15 K、I=35 A 代入考虑交互项的加速应力模型即式(21)中,可得预测结果L2=1 023 369。
根据加速实验数据分析可知,常规实验的特征寿命为L0为110.44 万次。
预测准确率为:
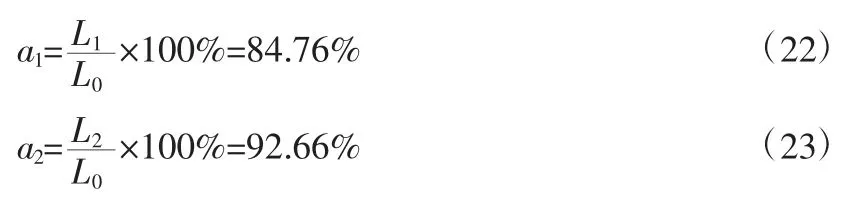
其中,a1、a2分别为不考虑温度与电应力交互项与考虑交互项模型的预测准确率。通过常规实验特征寿命验证,含交互项的复合应力加速模型相较于不含交互项的复合加速模型寿命预测准确率提升了7.9%。
5 结束语
本文通过接触器的加速试验对接触器的可靠性进行研究,结合接触器额定运行工况以及加速实验的研究,设计并完成温度和电应力的复合应力加速试验。通过对接触器加速实验下失效样本寿命进行分析,计算出为威布尔分布模型及各个加速条件下的样本特征寿命。
通过样本特征寿命分别推导出不含交互项和考虑交互项的复合应力加速模型,并对模型参数进行求解。利用两种加速模型分别映射到常规实验条件计算特征寿命。通过对比分析,证明相较于忽略应力交互项的模型,考虑温度和电应力之间影响的复合应力模型对接触器寿命预测准确率提升了7.9%,对接触器的寿命预测方法及加速应力模型具有指导作用。
基金项目:中国铁路总公司科技研究开发计划项目(编号:P2018J001)。
